基于最小弯曲能量法的斜拉桥索力优化

徐 冰 霜

(武汉科技大学城市学院，湖北 武汉 430083)



基于最小弯曲能量法的斜拉桥索力优化

徐 冰 霜

(武汉科技大学城市学院，湖北 武汉 430083)

以大悟县环水河人行景观桥为例，总结了斜拉桥索力优化的目标，采用最小弯曲能量法对实例斜拉桥的索力进行了计算和研究，以主梁弯矩和整体位移为控制目标，对索力进行了优化，得到了能够指导施工的有效的索力结论。

斜拉桥，索力优化，最小弯曲能量法，矩阵

0 引言

斜拉桥因其跨越能力大，结构受力性能好，造型多样的优点而被广泛的应用于现今桥梁建筑中。在斜拉索作用下，整座桥梁可以作为具有多点连续支撑的连续梁，通过人为调整拉索张拉力用以适应不同阶段和状况下的结构受力情况，实现整体结构受力最优的状态。所以，斜拉桥设计的关键在于斜拉索的索力计算与优化。斜拉桥索力优化计算的方法有很多种，常见的有恒载平衡法、连续梁法、最小弯曲能量法。由于最小弯曲能量法计算出的索力分布较为均匀、结构受力满足要求，文中采用该方法结合工程实例进行了斜拉桥索力计算并进行优化，为施工索力的确定提供依据。

1 索力优化目标

斜拉桥索力优化在于结构整体受力优化，能够反映结构受力状态的指标常常是指构件的弯矩、应力和位移。具体控制目标常常表现在以下方面：

1)索力分布满足索力呈递增的变化趋势，短索的索力小、长索的索力大；某些局部位置可以突变，如全漂浮体系斜拉桥的0号和1号拉索，为控制整体纵向位移其索力较大。2)恒载作用下的成桥主梁弯矩均匀且不出现较大的突变，控制在可行范围内。3)为保证成桥状态最优，主塔向边跨侧需要设置一定的预偏量用以抵消荷载和混凝土收缩徐变的作用。4)支座在运营阶段不出现负反力，可采用在边跨梁内增加配重或设置拉力支座的方法。

2 最小弯曲能量法

最小弯曲能量法以结构的弯曲能量最小为优化目标，设计目标函数使得桥梁结构整体的弯曲应变能最小，令其对索力的偏导为零，求解方程得到恒载下的合理成桥索力值。

如图1a)所示为斜拉桥成桥状态的计算模型。利用最小弯曲能量法计算索力时，将斜拉索截断，利用赘余力来代替斜拉索的作用，如图1b)中x1,x2,x3,…,xn-1,xn所示。

假设斜拉索的索力为xi=1，此时任意截面的弯矩为mi，恒载作用下基本结构的弯矩为MP。则任意截面的总弯矩为：

(1)

主梁中的弯曲应变能为：

(2)

弯曲应变能与索力xi有关，若要使U最小，令其对索力的偏导为0，即：

(3)

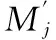
(4)

主梁结构的弯曲应变能表示为:

(5)

m个截面的弯矩矩阵可表示为：

[M]m×1=[M′]m×1+[m]m×n[X]n×1

(6)

目标函数为主梁弯矩应变能，对U求偏导，可得n个方程组:

(7)

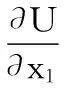
[m′]n×m·[M]m×1=0

(8)

即可求得索力矩阵，求得索力关系值如下：

(9)

为了使得计算的成桥索力能够使得斜拉桥处于合理成桥状态，可将索力值代入式(1)中，计算出此时结构主梁的弯矩值，得到结构弯矩内力图。

3 计算实例

3.1 实例概况

以大悟县环水河人行景观桥为实例进行研究分析。桥梁全长13.14km，跨径布置为22m+20m引桥+30m+66m+30m主桥+20m+25m引桥。主桥为三跨双塔双索面人行斜拉桥，如图2所示，主桥主跨66m，桥塔高28.6m。

3.2 索力计算

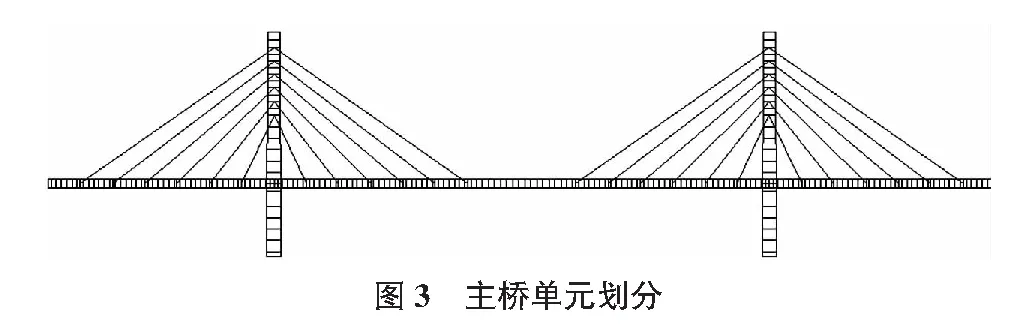
斜拉桥共有斜拉索24对，按照其所在位置进行命名，位于桥塔外侧命名为B1～B6，桥塔内侧命名为A1～A6。最小弯曲能量法需要对桥梁每一个截面和每一根斜拉索的索力进行分析，实际计算中结合有限元的方式进行，将全桥进行单元划分：主梁划分为201个单元，编号为1～201；模拟单侧斜拉索24条，编号为202～225,如图3所示。

按照最小弯曲能量法的计算原理，其过程是使用赘余力代替斜拉索的拉力，求解出使得结构整体弯曲应变能最小的索力。为了清楚地表示出索力对主梁的影响，取3号～200号节点所在截面，共198个截面作为研究对象。采用矩阵的方式求解索力的过程，先求解出自重、恒载及配重作用下的截面弯矩得到弯矩矩阵[M′]198×1；分别加入单根斜拉索，设置张拉力为xi=1，得到截面的弯矩mi，得到关系矩阵[m]198×24。式(9)表示索力矩阵解析关系：

(10)

将计算出来的[M′]198×1，[m]198×24代入式(10)中，利用Matlab进行矩阵求解，得到索力矩阵[X]24×1，即为该方式计算出的成桥索力值，如图4所示，基本上满足索力均匀、长索索力大、短索索力小的原则。

3.3 索力调匀优化

实际桥梁在施工的过程中，混凝土的收缩徐变及温度应力也会产生相应的应力效果，为了保证成桥状态索力最优，所以需要进一步考虑这些因素的影响进行优化调匀。优化后的成桥索力见表1。

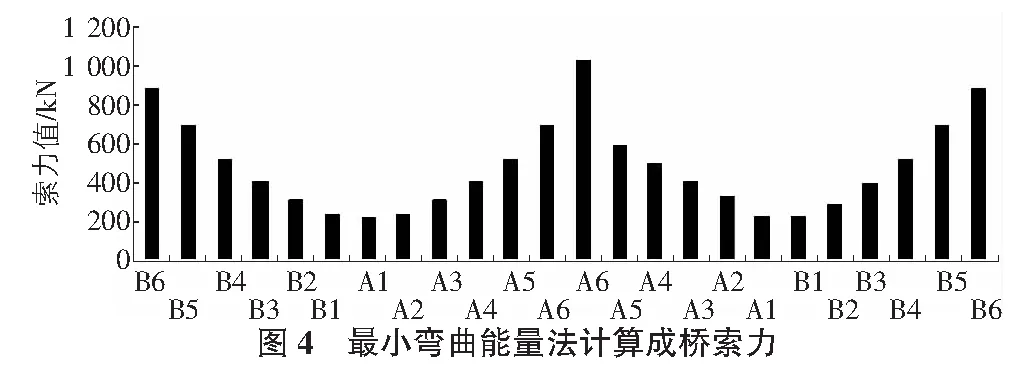
表1 优化后的成桥索力 kN

在该索力作用下，可以得到恒载作用下，主梁的弯矩图如图5所示，结构的位移变形图如图6所示。结构整体的弯矩图中(见图5)，弯矩下部受拉为正，说明斜拉桥的结构受力基本上能够满足合理成桥索力优化计算的目标，主梁受力均匀，没有较大的跳跃；整体结构的位移变形图中(见图6)，结构变形符合合理成桥状态的控制原则和目标，满足主塔向边跨处预偏，主梁有向上的与预拱度的要求。

4 结语

以大悟人行斜拉桥为实例，利用最小弯曲能量法原理，结合有限元思路进行全桥索力优化计算，取得了较为理想的结论。该过程中，以其成桥状态优化的主梁主塔的弯矩为控制目标，索力大小为约束条件，优化斜拉索的索力；通过内力和变形计算，最终得到主塔无弯矩、主梁变形符合要求的结果。该过程表明，最小弯曲能量法可以作为斜拉桥索力优化计算的一种有效方式，能够为斜拉桥的设计施工提供有效的索力结论，可以较为广泛地应用于实际工程项目。

[1] 陈明宪.斜拉桥建造技术[M].北京:人民交通出版社,2003.

[2] 张海龙.桥梁的结构分析·程序设计·施工监控[M].北京:中国建筑工业出版社,2003.

[3] 邵旭东,程翔云,李立峰.桥梁设计与计算[M].北京:人民交通出版社,2006.

[4] 梁 鹏,肖汝诚,张雪松.斜拉桥索力优化实用方法[J].同济大学学报,2003,31(11):1270-1274.

On cable force optimization of cable-stayed bridge based on least bending energy method

Xu Bingshuang

(Urban College, Wuhan University of Science and Technology, Wuhan 430083, China)

Taking Huanshui River pedestrian landscape bridge in Dawu County as the example, the paper adopts the least bending energy method to calculate and research the cable force of the cable-stayed bridge, optimizes the cable force by taking the upper beam bending moment and overall displacement as the control target, and achieves the effective cable force to direct the construction.

cable-stayed bridge, cable force optimization, least bending energy method, matrix

1009-6825(2017)16-0190-02

2017-03-22

徐冰霜(1990- )，女，助教

U448.27

A