混沌系统均匀化的浅析

李雪松

摘 要：本文通过复合混沌系统改造和设计变换函数，实现混沌系统的均匀化改造。从理论论述和数值测试两方面说明了改造后的均匀化效果。均匀化改造，有利于混沌系统在更多领域的实际应用，具有重要意义。

关键词：混沌系统；复合；函数变换

中图分类号：O415.5 文献标识码：A 文章编号：1671-2064（2017）11-0224-01

混沌系统是非线性动力学系统特有的一种运动形式，具有初值敏感性，非周期性。混沌系统的优良性质，为其在密码学的应用留下了广阔的空间。

在基于混沌系统的加密中，利用混沌系统产生均匀化加密序列是一个重要课题。产生均匀化的加密序列，能有效阻止破译者找寻到加密序列的数据分布规律，从而保证了明文的保密性。目前，只有Tent映射等几个混沌映射的概率密度是已知的.混沌系統的概率密度研究具有十分重要的意义.利用概率密度函数从而实现均匀化改造，可以从本质上改进混沌系统，将其应用在加密领域。

1 复合混沌系统均匀化

本文以如下两个混沌系统为例，在上 和给定序列，两个混沌迭代系统则其复合迭代系统为。

利用Perron-Frobenius算子分别求解两子系统的概率密度为和。当两子系统出现频率均为0.5时，复合系统的概率分布密度为1，则其实现了均匀化改造。

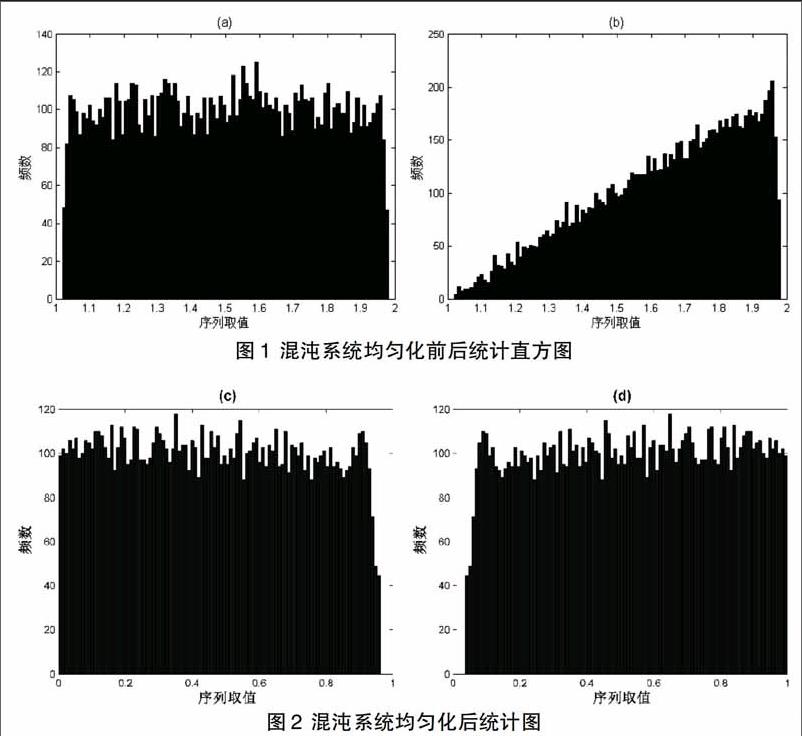
定义初始值为，分别复合迭代10000次，画出迭代序列的统计直方图，见图1。通过对比产生的随机序列可以清楚的看出，复合后的混沌系统能产生均匀化良好的序列。

2 变换函数均匀化

基于概率密度的形式，给出可逆变换，从而实现均匀化改造。

以1中两系统为例，分别设计变换函数和。依概率密度可得，通过函数变换后的系统概率分布密度均为1。从而实现了混沌系统的均匀化改造。图

2是两个混沌系统分别均匀化后产生的分布图，通过实验可以进一步确认均匀化效果。

3 结语

本文采用两个一维混沌系统，通过计算给出了该系统的概率密度。采用两种均匀化方法，实现混沌系统的均匀化改造，分别是复合函数构造，设计变换函数。经过计算证明，改造后的系统均具有均匀分布的概率密度。从而，在保证混沌特性不变的前提下，改造了原系统的均匀性。

参考文献

[1]禹思敏.混沌系统与混沌电路——原理、设计及其在通信中的应用[M].西安：西安电子科技大学出版社，2011.

[2]李佩玥，石俊霞，郭嘉亮，陈雪，杨怀江.一种混沌伪随机序列均匀化普适算法的改进[J].电子学报，2015，Vol.43，No.4：753-759.

[3]李红达，冯国登.复合离散混沌动力系统与Hash函数[J].计算机学报，2003.4，Vol.26， No.4，460-464.

[4]郝柏林.从抛物线谈起—混沌动力学引论[M].北京：北京大学出版社，2013.