运用ARMA模型预测河口县渡口监测点位五日生化需氧量污染趋势

关锐

摘 要：本文讨论的主要问题是时间序列分析和在环境监测污染预测范围的应用。本文使用了红河州河口县红河某个支流河流的单一点位的六年数据，使用时间序列arma（自回归滑动平均模型）模型对该河流单一点位渡口进行模型拟合。并使用拟合出的arma（3，3）模型对该点位未来两年数据进行预测，并对2005到2013年的数据也做了预测，并把2005到2013年预测的数据与2005到2013年预测的数据进行对比，发现平均误差为8.25%，达到可接受水平，所以该模型可以用来对该点位的五日生化需氧量，进行污染预测，预测的数据能很好的帮助环境管理决策。

关键词：环境监测；污染；时间序列；arma；预测

中图分类号：X52 文献标识码：A 文章编号：1671-2064（2017）11-0011-02

1 时间序列技术和ARMA模型介绍

1.1 时间序列

所谓的时间序列是用时间记录列表排序的数据为研究依据，观察时间序列，寻找他的改变轨迹，预测其未来发展趋势。在日常生产、生活中，时间序列应用比比皆是。作为数理统计学的一个专业分支。时间序列遵循数理统计的基本原理[1]。

1.2 ARMA基本概念

广泛稳定：随着时间的推移，该序列的统计特性不改变只是时间间隔相关。AR模型：AR模型另外的称呼为自回归模型，回归模型预测过去和现在的观测干扰值是一个数学公式的方式线性组合。自回归模型的数学公式为：

式（1）中：y为自回归模型的阶数（i=1，2，...，p）为模型的待定系数参数，ξ为误差，序列为一个平稳时间序列。

MA模型：MA模型也称为滑动平均模型。它对数据预测形式是通过过去和现在的干扰干扰值预测值的线性组合。数学公式移动平均模型：

式（2）中：q是这个模型的阶的系数；（J=1，2，...，q）为待定系数模型；ξ为平均误差；函数为平稳时间序列函数。

ARMA模型：自回归模型和滑动平均模型的组合，便构成了用于描述平稳随机过程的自回归滑动平均模型ARMA，数学公式为：

2 建模与预测内容及假设

2.1 假设

（1）假设：河口县GDP保持年均每年增长12%以上，人口自然增长率控制在每年4‰以内；（2）假设河口县大部分排污企业达标排放，大部分生活污水得到收集；（3）认为未来将不会有大的污染事故和其它不可抗拒的自然和社会因素。

2.2 内容

（1）依据时序图来确定序列的稳定性；（2）考察有关图，初阶确定移动平均阶数q和自回归阶数p；（3）利用经典B-J法利用红河州八年水质数据建立适当的ARMA（）模型，并利用该模型进行短期预测。

2.3 绘制序列时序图

我们对序列做ADF检验，出现序列图1所示，时序图得到108个数据因为序列没有明显的上升和下降趋势，所以是稳定的，判断是粗糙的，需要用统计方法来验证[2]。

2.4 ADF检验序列的平稳性

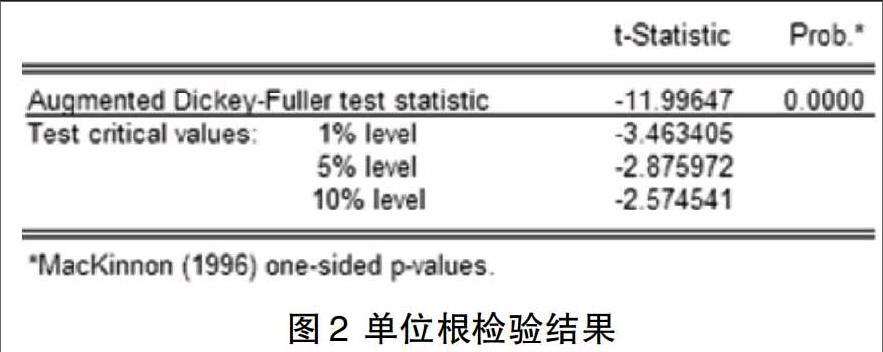
由时序图和相关图，以确定该序列是平稳的，我们通过统计检验，以进一步证实这一结论，双序列生产，点击查看/单位根检验，在图1的对话框中的外观，我们发现该序列本身没有明显的波动趋势，所以选择常数项，做没有倾向测试模型的选择，其他使用默认设置，试验结果表明，拒绝零假设，存在一个单位根平稳序列。单位根检验结果图2所示。

2.5 模型定阶

它是在偏相关系数当K=3快速向0收敛所以是3阶图，因此AR拟合（3）；图K=1的自相关系数为0，其置信带的边缘为K=3，标准偏差的2倍，所以考虑拟合ma（2）或ma（3）；在同一时间拟合考虑ARMA（3，1）模型。

2.6 模型参数估计

（1）尝试AR模型。经过模型识别所确定的阶数，可以初步建立AR（3），可用菜单或命令两种方式分别建立。在主菜单中选择快速/估计方程，在定义方程空缺区输入x ar（1） ar（2） ar（3），其中ar（i）（i=1，2…）表示自回归系数。在已知的伴随概率下，AR（I）（I =1，2，3）显著性很高，在表的底部给出的是滞后多项式的倒数根，只有当这些值都落在单位圆内，这个过程才是平稳的。由伴随概率可知，AR（i）（i=1，2，3）均高度显著，表中最下方给出的是滞后多项式的倒数根，只有这些值都在单位圆内时，过程才平稳。通过使用复杂根的检验理论的复数知识，知道三个根都落在单位圆。AIC，SC准则是重要的标准在选择模型中，在比较中，我们希望这两个指标能最小。DW统计量是对残差的自相关检验统计量，在2附近，说明残差不存在一阶自相关[3]。

（2）尝试MA模型。根据上述定义，方法，方程类型的空白区域键入X ma（1）ma（2）（当中（MA（J），J=1，…代表移动平均系数）或在主菜单视窗键入ls x ma（1） ma（2）。从MA（2）伴随概率的估计结果，系数不显著，因此消除，继续做估计模型。该表的底部是多项式 的根滞后的倒数，惟有这些值都落到单位圆内，整个方程是个平稳的过程，可以发现，它满足方程的要求，即稳定。

2.7 尝试ARMA模型

通过模型发现，P可以等于3，Q值可以等于3，根据不同的组合来选择优化模型，在主菜单视窗命令栏键入ls x ar（1） ar（2） ar（3） ma（1），敲击回车，即获得参数估计见图3所示。

从参数估计的结果可以看出，该系数不显著，表明该模型是不适合ARMA（3，1）模型。经过进一步甄别，并删除不明显逐渐滞后或移动平均期限，因此最后得到下面的ARMA（3，3）模型：

Y（t）=-0.222189*Y（t-1）-0.139276*Y（t-2）-0.917088*Y（t-3）+e（t） -0.097127e（t-1） -0.096037*e（t-2） -0.998908*e（t-3）+1.532543

由以上我们可以知道，我们能够根据原则创建一个更合适的模型，一样的平稳序列，但数值对比AIC和SC，和酌量其余的检验统计量，基于ARMA模型的简单的规定，所以ARMA（3，3）模型是最佳的选择。

2.8 模型预测

静态预测中，预测值存储在xf中，X和XF图4部分所示，我们可以看到静态预测效果很好。

根据2013年的预测结果，相对误差及预测精度整体上各期的预测值与实际值间的相对误差较小，根据计算均值绝对百分误差为8.1087，说明模型的预测效果较好。

2.9 預测误差分析

对于使用ARMA模型进行水质污染分析，我们是在不考虑众多影响水质的因素的条件下进行，但是在实际中红河州的河流水质污染是整个存在有不确定性成分、变化比较难以预测的情况，因此就会有一定的误差。另外，水质污染预测是一种有条件的预测，是假定工业企业、人口增长、面源污染、天气气候等的影响变化基本是在过去变化基础上的延伸或重复，但在实际中往往并非如此，社会环境在不断变化和发展，工业企业、人口增长、面源污染、天气气候影响因素在不断产生与变化，所以造成了预测结果与实际结果的偏差，产生了一定的误差。当然造成误差的原因还很多，如计算上有差错，或者建立的预测模型不够精确等等。

3 结语

以ARMA模型分析为主，对河口县渡口断面五日生化需氧量进行了预测和对比分析，取得了良好的效果，显示了ARMA模型在河流污染物预测有着广阔的应用前景。通过对ARMA时序模型用于预测研究进行深入的了解，我们也发现了一些不足之处，比如说ARMA模型只考虑在一段相当长的时间内数据的相关性，就是说只考虑了数据的时间维度，而忽略了其他因素，这在一定程度上便于预测和使用，但在实际中，河流的污染因子是由很多因素造成的，所以ARMA模型预测的准确度和可用性在一定程度上还有待研究。

参考文献

[1]田铮.时间序列的理论与方法[M].北京：高等教育出版社，2001.

[2]何书元.应用时间序列分析[M].北京：北京大学出版社，2005.

[3]潘红宇.时间序列分析[M].北京：对外经济贸易大学出版社，2006.