三自由度直升机多模型LQR控制器设计


摘要 通过对三自由度直升机模型实验系统的总体分析,引入了多模型切换思想,建立了多模型LQR控制器。针对多模型LQR控制器将数学模型以高度角和俯仰角两个角度为变量建立多模型集合,运用Matlab搭建仿真对控制器进行仿真实验,并通过直升机高度角、俯仰角和旋转角的跟踪准确性、快速性以及超调量大小等控制指标,直接地度量控制器控制效果的好坏,将控制效果最优的多模型LQR控制器应用于直升机实物模型之上,运用Matlab中的实时工作空间(RTW)和Quanser公司专用控制软件Wincon实现对直升机实物的实时控制,控制效果良好。
关键词 三自由度直升机模型;LQR控制器;多模型LQR控制器
中图分类号 TP2 文献标识码 A
Summary:In this paper, the multi-model set of 3-DOF is built, based on model switch idea and the LQR controller is established by analyzing the whole helicopter system. The multi-model set is achieved and differed by high angle and pitch angle and the controller is designed and simulated in Matlab. With the real-time value of control variables, the performance of the designed controller is shown. The real controller is built in Matlab RTW with the help of Wincon software interface of Quanser. The results of the simulation is shown the effectiveness of the designed system.
Key Words:3-DOF helicopter model; LQR controller; multi-model LQR controller
引言
二十世紀七十年代末我们开始了对直升机的研究,分别从美法等直升机研究水平处于世界领先地位的发达国家引进了诸如“Black Eagle”和“Apache”等成熟的直升机机型。但是长久以来我们的努力只是停留如何去模仿别人,最多达到在别人的基础上稍作修改,并没有真正在直升机的技术核心领域获得成功,比如直升机飞行最为核心的操控系统,就鲜有成绩,这就给后来学者和研究人员提出了更高的要求,促使我们进一步探索[1]。
在国内高校方面,研究本课题的有:东北大学的刘鑫,首先针对直升机设计PID控制器,然后设计直升机系统的模糊控制器,最后将两者合二为一,设计出模糊控制和PID控制相结合的控制方法,取得良好效果;山东大学的葛金来,他不但设计了PID和LQR控制器,还对直升机模型有无动态干扰模块(Active Disturbance System, ADS)扰动进行了实验,最后还对直升机模型进行了基于保性能的控制研究[13];国外的,如Jonas Witt利用非线性近似模型预测控制设计控制器;Ali T. Kutay完成了通过自适应输出的反馈控制;Konstantin K. Starkov则针对非线性系统设计了一种滑模控制器来实现控制;Mitsuaki Ishitobi也在前人基础上利用参数辨识的方法进行了一系列闭环控制。以上控制方法都没有对直升机模型系统进行建模,而是利用非线性系统的理论分析方法来设计控制器。但是,非线性理论本身就不是一套完善的理论,所以在设计控制器时不可避免的存在一些近似或者忽略次要影响因素,导致真正的实时控制在精度上并不那么让人满意,绝大多数仍只是停留在仿真的阶段,但是对要求不是十分苛刻的系统仍然具有较大的参考指导价值。
本文主要以加拿大Quanser公司研发制造的三自由度直升机模型为实验平台,基于系统自带的Matlab-RTW(Real-Time Workshop, RTW)实物仿真控制系统,在此开发环境下对双旋翼三自由度直升机模型进行深入理论研究,并运用理论成果设计新型控制器达到控制直升机模型位置和飞行速度的目的。
1三自由度直升机模型实验系统的结构组成
本实验系统作为研究纵列式双旋翼直升机的仿真平台,在结构上主要由硬件系统和软件系统两部分组成。其中,硬件系统又包含机械控制系统和电气控制系统两部分。控制过程可简单描述如下,直升机飞行姿态通过数据采集卡传递给计算机,计算机对各变量进行实时处理,然后将控制指令通过运动控制卡传递给电源模块来控制直升机驱动电机的供电电压,以此来调整模型的飞行姿态。整个实验系统可以用如图1所示的框图来清晰地表示出来。
1.1直升机模型硬件系统
本文所使用的Quanser公司三自由度直升机模型实验系统的硬件系统由直升机本体、电源模块、数据传输线、数据采集卡和一台计算机组成。其中,直升机本体属于硬件系统中的机械控制部分,数据传输线、数据采集卡、电源模块和计算机属于硬件的电气控制部分。
1.2直升机模型软件系统
本文直升机模型实验系统采用的软件系统完全安装在一台实验专用计算机中,包括由Quanser公司自行开发的基于Matlab中Simulink软件包和TCP/IP技术的控制软件Wincon[2]和从Simulink生成优化而来的RTW实时工作空间。
2基于多模型切换的LQR控制器设计
2.1 多模型控制方法的基本原理
多模型控制主要由以下三部分组成:
2.2多模型控制器的构成
在运用多模型控制理论建立控制器的过程中,大致只有两个步骤,那就是针对模型集中的每个单一模型建立最为适合的控制器,然后运用诸如模型切换或加权平均的方法将这些控制器集中起来,完成最终控制器的设计,下面就对多模型控制器设计中最常用的两种方法简单讨论:
1) 通过加权建立多模型控制器[3,4]:方法需要运用到数学理论中的分割定理,根据每个独立模型的权重比例,运用概率加权的方法,得出最终的控制器。
2) 根据某种切换策略建立多模型控制器:保证控制器切换时的稳定性是此种方法的首要前提,由于该方法相对第一种方法较为直接,设计难度也不大,所以各类研究成果层出不穷[5,6]。
本文的研究过程中,运用到的就是上文介绍的第二种多模型研究方法,即模型切换的控制策略。
2.3三自由度直升机多模型LQR控制器设计
围绕研究对象三自由度直升机模型实验系统,根据模型的实际变化特性来建立多个模型,组成一个合理的多模型集合,尽量逼近直升机系统在飞行过程中的真实动态性能,再基于此多模型集合设计出多模型控制器集合,最后根据真实飞行状态的不同选取最逼近当前状态的模型,用其对应的也就是最适合当前直升机状态的控制器来实施控制策略,从而实现对复杂系统进行更有效控制的目的。
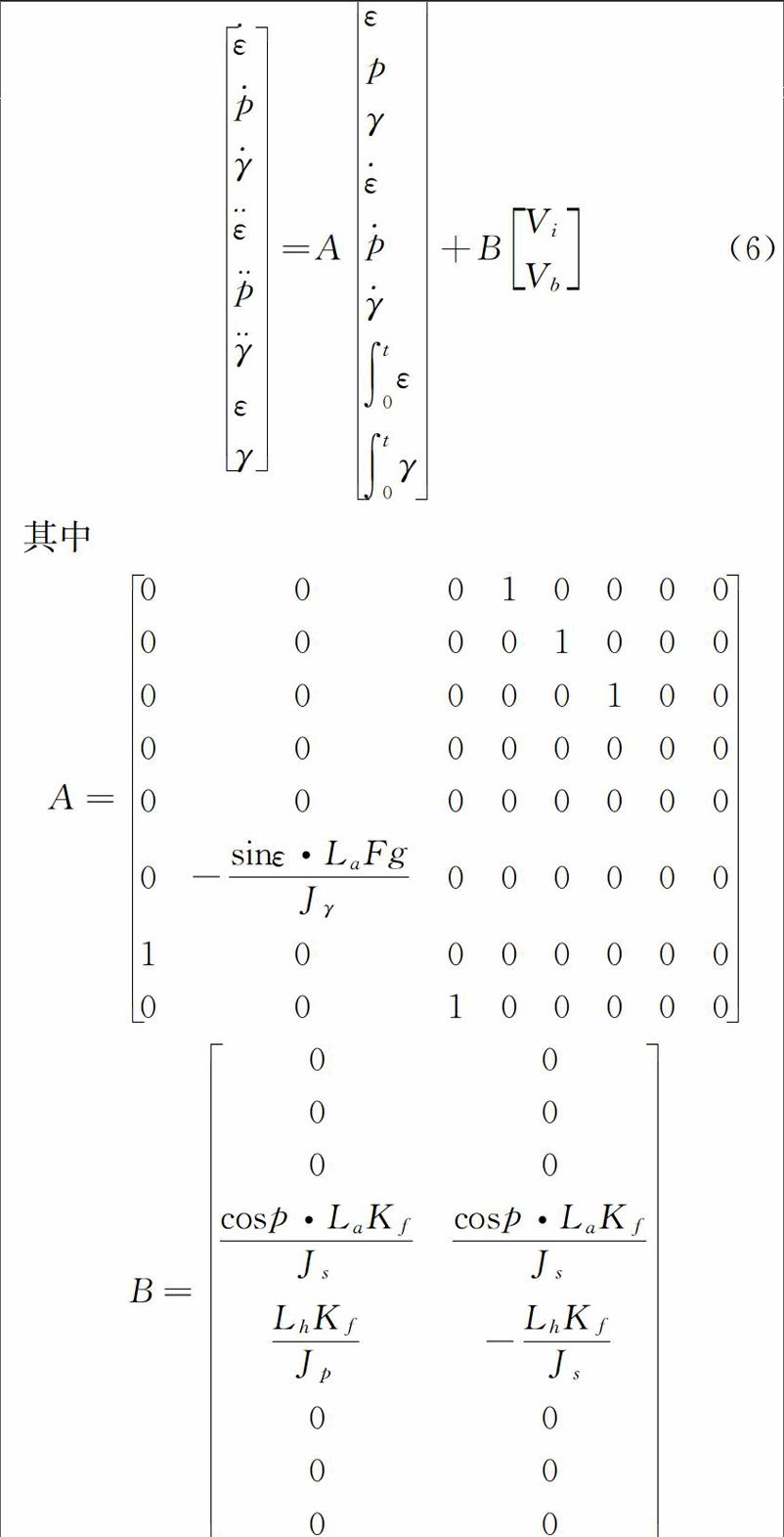
由此,结合直升机模型飞行过程中的实际情况,采用模型切换的思想,而不是模型加权理论,根据直升机飞行过程中的具体位置,建立适合当前系统的模型参数,同时设计多组LQR控制器,每组控制器都分别设定符合当前情况的 和 矩阵取值,得到最直接最有效的控制量,使得直升机跟踪给定信号既快速又准确。控制方法结构框图如图2所示。
2.3.1 多模型集合的建立
在多模型控制理论的实现过程中,首当其冲的难题就在于如何针对控制过程建立清晰明确的数学模型,在实际研究过程中,只能把系统的输入输出作为切入点,采用一些常见的辨识方法,例如非线性自回归滑动平均模型等。先分解再合成的多模型控制策略就可以对这个问题有一定程度的解决,有些结构复杂的对象系统,无法得出能够包含整个控制域的模型,所以采用分段方法,对每个分段区域建立恰当的模型,然后将这些分段模型进行数学处理,无论是加权还是切换,都是可行的手段。这种方法主要包括两个大的方面:一是将问题进行分解;二是运用恰当方法进行合成。详细步骤可以按以下操作:
1) 引入一种恰当的规则,对整个控制域进行分解,分成符合要求并且结构较为简单的几个部分;
2) 针对每个部分建立数学模型和控制器;
3) 终极目标则是选取一种合适的方法,将之前分解的分段模型和控制器进行有效组合,得出最终结果。
通过查阅大量相关文献,了解到在多模型方法建立模型集合的领域内,非线性系统的线性化[7]、T-S型模糊多模型[8-10]、神经元网络多模型[11]、即时学习算法[12-16]等手段应用较为广泛,效果也很明显。
针对Quanser公司三自由度直升机模型实验系统的结构特点,再在原有数学建模的基础上,加深对实验系统物理特性的分析,将之前的近似和线性化重新考虑起来,建立其更为准确的数学模型。将直升机的高度角 和俯仰角 作为多模型集合建立的切入点,得出多模型LQR控制器的多模型集合,如表1所示。
3.1直升机模型实时控制
整个实物仿真过程的实现大致可以分成以下三个部分:
1) 控制算法的编写和控制器的搭建,这一步的完成与我们之前的仿真控制器设计是类似的,都是利用了Matlab中的.m文件和Simulink工具包,使得研究人员可以方便直观地调用Matlab中强大的模块库来简化整个设计过程;
2) 在将控制算法的编写和控制器的设计完成之后,可以直接通过Matlab-RTW实时工作空间自动完成从便于研究人员设计的模块化程序化的框图语言向便于机器识别和运行的语言的编译转化过程;
3) 最后,通过Quanser公司自己研发的基于Matlab中Simulink软件包和TCP/IP技术的控制软件Wincon,将编译好的控制语句作用在通过编码器和数据传输线连接在数据采集卡和电源模块上的三自由度直升机机体上,实现控制直升机模型实物的最终目的。
3.2 LQR控制器和多模型LQR控制器仿真及实物控制效果对比
单一模型LQR控制器和多模型LQR控制器在Simulink仿真以及后续实物平台的控制效果进行对比和分析。
首先在Matlab中用单一模型LQR控制器对直升机模型进行仿真实验,在仿真的初步阶段,采用较为简单的函数曲線作为给定信号。
将一个周期为100秒幅值为20的正弦信号作为高度轴的给定信号,单一模型的LQR控制器跟踪效果如下图3所示。
同样的,将相同的周期100秒幅值20的正弦信号作为给定信号,用所设计的多模型LQR控制器来进行高度轴的飞行跟踪控制,结果如图4所示。
通过上面的图3和图4的对比,可以非常清晰地发现,单一模型LQR控制器在跟踪正弦函数曲线的过程中超调量较大,调节时间较长,在两个周期也就是仿真时间到达200秒的时候才能达到较好的跟踪效果,而多模型LQR控制器的表现就大大优于单一模型LQR控制器了,不仅在50秒左右就能够很好地跟踪上给定信号的变化,而且在调节的过程中超调的幅度也是远小于单一模型LQR控制器的。
在完成对两个控制器的初步仿真实验之后,接下来就要进行更加复杂的实验,将给定的函数信号变为阶梯方波便是最有效最合理的方式。因为阶梯方波是一组不停变化的信号,这样就对直升机在飞行时不断变换飞行姿态时的实际需求进行了很好的模拟。同时,阶梯方波又可以在一段时间内保持平稳,恰好又符合飞机飞行过程中有大段时间平稳飞行的实际。所以,阶梯方波是能够完美模拟直升机真实飞行状况的良好跟踪信号源。
在实物仿真中,采用对直升机实际飞行最具有仿真性和现实意义的阶梯方波作为给定信号,高度轴和旋转轴的跟踪效果分别如图5和6所示。
从实物曲线可以看出,多模型LQR控制器运用在直升机实物上表现依旧让人满意,说明我们设计的控制器是相当成功的。
4结束语
本文首先介绍了Quanser公司三自由度直升机模型实验平台的结构组成,并对硬件系统和软件系统分别进行了介绍。通过对于多模型控制的研究,将多模型LQR控制器的设计重点放在了通过模型切换思想实现多模型控制上。之后针对多模型控制建立多模型集合的需求,对之前直升机模型的数学建模进行了优化,在微分方程中恢复了之前被近似化忽略掉的角度影响因素,并针对高度角和旋转角两个角度变量设计多模型集合,同时对应每个模型设计LQR控制器,得到一个LQR控制器集合,完成多模型LQR控制器的设计。通过实际仿真的效果对比,多模型控制器的优势得到很大发挥,控制效果明显优于单一模型的LQR控制器。而在随后的直升机实物控制中,多模型LQR控制器的表现仍然很好。
参考文献
[1] 刘广磊,申涛. 三自由度直升机多模型LQR控制方法[J]. 济南大学学报(自然科学版),2014,28(1):45-49.
[2] 吴森堂,费玉华. 飞行控制系统[M]. 北京:北京航空航天大学出版社,2010:105-136.
[3] 周焕银,刘开周,封锡盛. 基于权值范围设置的多模型稳定切换控制研究[J]. 控制与决策,2012,27(3):349-354.
[4] Erin M. Aylward, Pablo A. Parrilo, Jean-Jacques E. Slotine. Stability and robustness analysis of nonlinear systems via contraction metrics and SOS programming[J]. Automatica,2014,44: 2163–2170.
[5] Mitsuaki Ishitobi, Masatoshi Nishi . Nonlinear Model following control with parameter identification for a 3dof model helicopter[J]. Advanced intelligent mechatronics,2009,32:253-267.
[6] Zhivoglyadov PV, Richard HM, Fu MY. Further results on localization-based switching adaptive control[J]. Automatica,2011,37:257-263.
[7] 马娟丽. LQR系统最优控制器设计的MATLAB实现及应用[J]. 石河子大学学报(自然科学版),2013,23(4):519-521.
[8] Patton R J. Synchronization of decentralized multiple-model systems by market-based optimization[J]. IEEE Trans. Systems, Man and Cybernetics, Part B, 2004, 34(1): 665-671.
[9] Patton R J, Lopez Toribio C J, Simani S. Robust fault diagnosis in a chemical process using multiple-model approach[C]. Proceedings of the 40th IEEE Conference on Decision and Control. Orlando Florida USA, Expert Systems with Applications .2010: 349-354.
[10] Yang Haiqing, Yu Li, Xu Chi. Multiple model adaptive control of automatic quasi-synchronization for 500 kW hydropower generator[C]. Intelligent Control and Automation, 2004. WCICA. Fifth World Congress on, Hangzhou, P.R. China, Automation in Construction . 2004:5112-5115.
[11] Jonas Witt, Sudchai Boonto. Approximate model predictive control of a 3dof helicopter[C]. Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans, SPIE .2007:1243-1251.
[12] Konstantin K. Starkov, Luis T. Sliding Mode control synthesis of a 3dof helicopter prototype using position feedback[J]. Variable Structure Systems, 2008, 8:233-237.
[13] Bontempi G, Birattari M, Bersini H. Lazy learning for local modelling and control design[J]. Int. J Control, 2009, 72 (7/8): 643-658.
[14] Zheng Q B, Kimura H. Just-in-time modeling for function prediction and its applications[C]. Proceedings of the 3rd Asian Control Conference, Shanghai, China, Fluid Dynamics Research .2008:1816-1821.
[15] 尹秀云,李擎. 基于LQR最优控制系统的设计[J]. 微计算机信息.2012,23(1):55-57.
[16] 孙维,王伟,朱瑞军. 即时学习算法在非线性系统迭代学习控制中的应用[J]. 控制与决策,2003, 18(3):263-266.
联系方式
联系作者:孙莉
地址:濟南市历城区七里河小区35号楼4单元601
邮编:250100
E-mail: sunli2005sd@163.com
手机:13583113227
备注:开发票
发票抬头:山东协和学院

