光学元件研磨加工裂纹形成过程数值模拟

王洪祥， 严志龙， 王景贺， 周 岩， 白 桦， 翟文杰

(哈尔滨工业大学 机电工程学院，哈尔滨 150001)

光学元件研磨加工裂纹形成过程数值模拟

王洪祥， 严志龙， 王景贺， 周 岩， 白 桦， 翟文杰

(哈尔滨工业大学 机电工程学院，哈尔滨 150001)

针对传统有限元方法过度依赖于网格，计算时磨粒和工件接触区域的网格畸变严重，很难模拟脆性材料加工中材料内部裂纹的形成过程这一问题,利用光滑粒子流体动力学法建立单个磨粒切削加工过程的FE/SPH耦合有限元模型，对熔石英材料研磨过程进行数值模拟，为脆性材料切削过程的仿真提供了新途径. 系统分析研磨加工中亚表层裂纹的形成过程以及切削参数对亚表层裂纹深度的影响规律. 仿真结果表明:磨粒刚开始切入工件时材料处于弹/塑性变形阶段，随后在磨粒的挤压及撕扯作用下，材料内部产生大量微裂纹,微裂纹的合并、连通和扩展最终形成了平行于工件表面的横向裂纹和垂直于工件表面的纵向微裂纹，导致工件材料的脆性断裂去除.

熔石英元件；光滑粒子流体动力学；亚表面裂纹；研磨加工；脆性材料

在熔石英元件研磨加工过程中，外部载荷借助于游离于研磨盘和工件表面间隙中的磨粒作用于工件表面. 研究单颗磨粒-工件之间相互作用过程，能够更好地了解材料亚表层裂纹的形成及扩展过程. 然而,研磨加工过程中不同磨粒的刻划轨迹相互重叠、交叉，难以准确地区分单个磨粒刻划引起的裂纹形成过程，这为深入研究研磨加工中的裂纹形成和材料去除机理带来一定的困难[1-2]. 利用有限元技术对裂纹形成过程进行数值模拟，仿真结果直观、成本低. 但是传统的有限元法过度依赖于网格，计算时磨粒和工件接触区域的网格畸变严重，材料温度梯度和应力也往往会出现不连续变化现象，很难模拟脆性材料加工中材料内部裂纹的形成过程. 因此，需要寻找一种能够模拟脆性材料亚表面裂纹形成过程的仿真新方法. 光滑粒子流体动力学方法(SPH)不需要划分网格，因而避免了网格畸变的发生，且具有较高的计算精度，为解决上述问题提供了新途径[3].

本文利用光滑粒子流体动力学方法建立单个磨粒切削加工过程的FE/SPH耦合有限元模型，并对熔石英材料研磨过程进行数值模拟，分析材料内部裂纹的形成过程，研究切削参数对亚表层裂纹扩展深度的影响规律，寻找抑制亚表层裂纹扩展的有效方法.

1 SPH法基本原理及材料本构模型

光滑粒子流体动力学方法使用一系列任意分布的SPH粒子作为数值计算框架，粒子与粒子之间无需网格连接，因而不会发生网格畸变问题，同时也无需定义单元分离准则，可以很好地解决传统FE法存在网格变形严重、计算精度低和摩擦因数难以确定等问题[4-5]. 该方法使用具有一定质量粒子对被分析结构进行离散化，粒子的运动同样遵循质量、动量及能量守恒定律，材料变形可通过求解粒子组的动力学方程和跟踪粒子的运动轨迹来确定[6].

材料本构模型主要描述材料在不同载荷下的应力-应变关系，选用合理的材料本构模型是进行精确计算的前提. Johnson-Holmquist ceramic(JH-2)模型是一个能够描述脆性材料动态响应的本构模型，它依靠加入状态变量来处理材料内部的损伤问题，其材料屈服准则为微观裂纹的生长，而不是断层运动，可以用于模拟脆性材料损伤劣化力学行为[7-8]. 为了研究单颗磨粒切削熔石英时材料内部裂纹的形成过程，本文采用LS-DYNA材料库中的JH-2材料本构模型，熔石英玻璃的JH-2材料模型参数见表1[7].

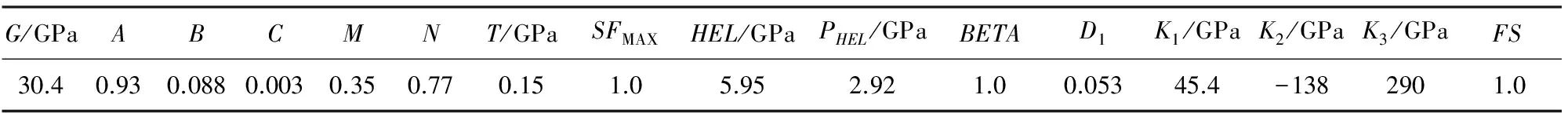
表1 熔石英玻璃的JH-2材料模型参数[7]

表1中G为材料切变模量，A、B、C、M、N为材料常数. 金刚砂磨粒的弹性模量和硬度远大于熔石英玻璃，在切削加工过程中变形很小，可将其视为刚体，其材料力学性能参数见表2[9].

表2 金刚砂的材料力学性能参数[9]

2 FE/SPH耦合有限元模型的建立

为便于模拟磨粒与工件之间的相互作用过程，可以将脆性材料的研磨加工过程抽象为尖锐压头在工件表面的刻划过程[10-12]. 尽管SPH法在模拟材料的大变形、大应变问题时存在较大优势，但其求解效率不高，而传统有限元法在计算连续介质的变形和应力方面具有更高的效率[13-15]. 由于金刚砂磨粒的硬度大于熔石英的硬度，为了提高计算效率，在不影响计算精度的前提下，对变形量很小的金刚砂磨粒采用网格法建模，而对发生较大变形的熔石英元件采用光滑粒子建模. 为了便于建模计算和将仿真结果与刻划实验结果进行对比，必须首先确定参与切削磨粒的几何形状. 本文设磨粒的刃口半径为0.5 μm、磨粒锐度角α为90°，建立了刃口半径为0.5 μm、磨粒锐度角α为90°的单个磨粒的有限元模型，选用显式非线性Solid 164实体单元，单元总数为4 000个. 为了减小计算量，只建立了切削区域内工件的SPH模型，工件的尺寸为30、24、0.3 μm，设置的SPH粒子总数为64 000个，金刚砂磨粒的FE模型与工件的SPH模型如图1所示.

本文将磨粒加工过程简化为磨粒在材料表面的直角切削过程，磨粒刀具沿X轴正方向作直线运动，因此需要约束刀具的全部旋转自由度及Z向平动自由度，而在X、Y方向施加位移载荷. 约束工件底部和右侧粒子的所有自由度， 以防止工件在仿真过程中因受力而发生移动. 对于SPH模型，不能通过边界点的约束来定义对称边界面，需要进行特殊处理. LS-DYNA通过创建虚粒子的方法来定义对称面，如图2所示，对靠近边界处2h(h为光滑步长)范围内的每个粒子，通过镜像自身，自动创建相应的虚粒子，两者相比，虚粒子具有相同的质量、压力和速度，这样虚粒子就处于真实粒子的支持域内，可以对相邻粒子近似产生作用[4]. 仿真时工件和磨粒间采用ENTS接触，并通过罚函数传递力学参数.

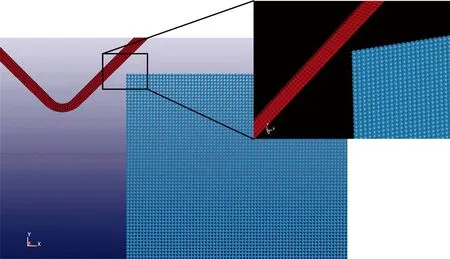
图1 金刚砂磨粒与工件的有限元模型

Fig.1 Finite element model of diamond abrasive grains and workpiece

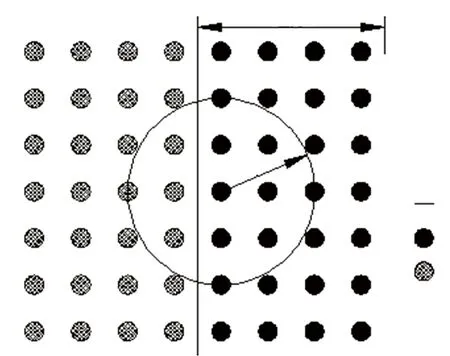
图2 SPH模型对称平面

3 材料去除及亚表层裂纹形成过程模拟

为了深入研究研磨加工工艺参数对亚表层裂纹扩展深度的影响规律，本文在一定条件下对磨粒切削过程进行数值仿真. 当切削速度νs为0.63 m/s、切削深度ap为3.5 μm、磨粒锐度角α为90°时，材料脆性去除和亚表面裂纹形成过程的仿真结果如图3和4所示.

(a) t=1.6 μs

(b) t=4.6 μs

(c) t=8.0 μs

(d) t=11.0 μs

由图3可见，在磨粒刚开始切入工件材料时,材料受到磨粒的挤压作用，位移最大的SPH粒子集中于磨粒与工件的接触面上，此时材料处于弹/塑性变形阶段(见图3(a)). 随着磨粒不断向前运动，与磨粒接触的SPH粒子数量随之增加，有大量SPH粒子脱离原位置被去除，同时在前刀面处的材料内部产生大量微裂纹，随着微裂纹的合并与连通，最终形成了平行于工件表面的横向裂纹(见图3(b)). 在磨粒进一步切入的过程中，横向裂纹在磨粒较大负前角的挤压及材料碎片的翘起作用下不断向前扩展，并向工件表面偏转，引起材料的崩碎、飞出，最终导致工件材料的脆性断裂去除(见图3(c)和(d)). 分析发现，由于横向裂纹在此阶段不断向前扩展，材料不断崩碎飞出，使得接触区内部的应力得以释放，最终在工件上只产生了较小的亚表层裂纹.

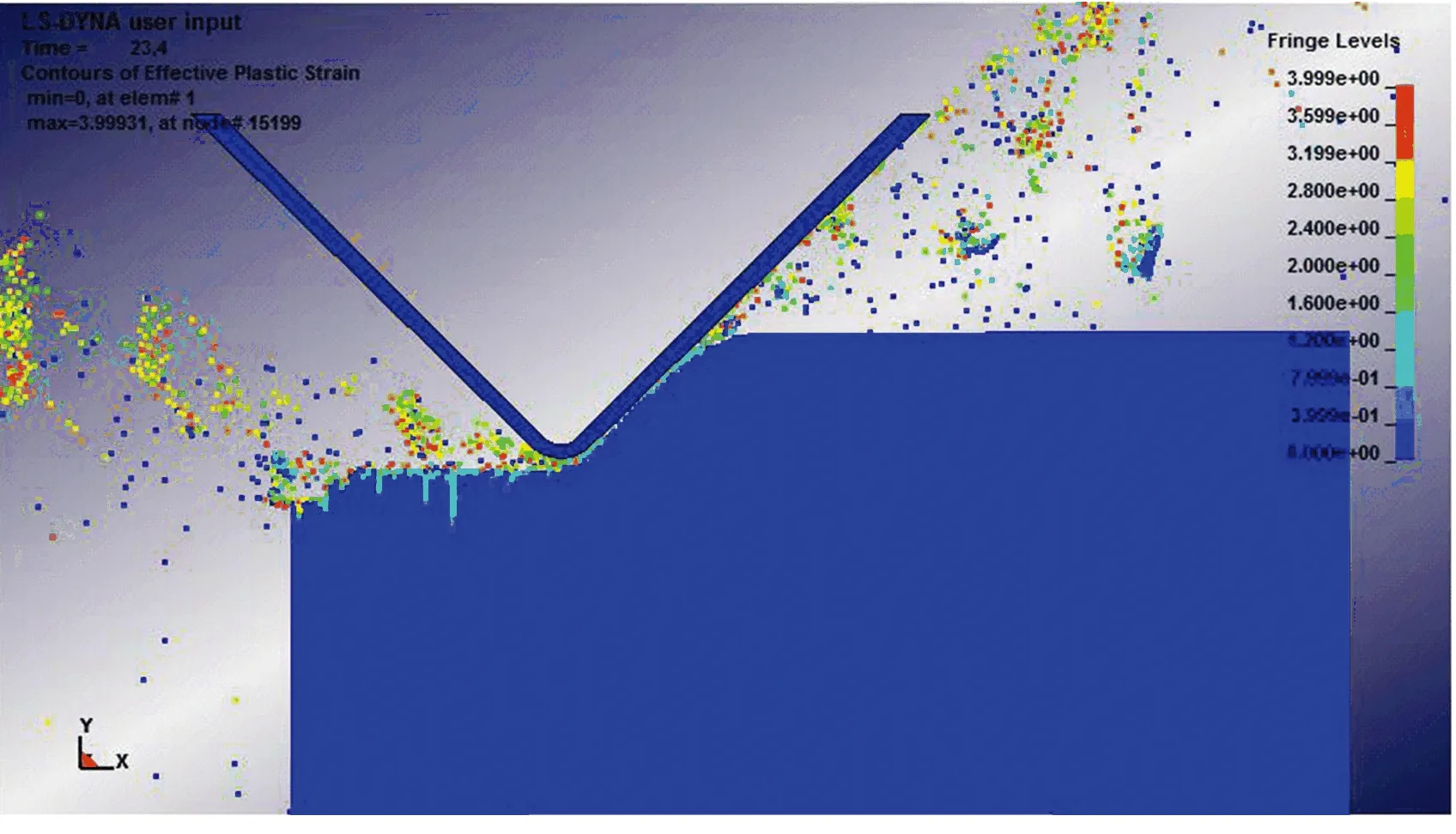
(a) t=23.4 μs

(b) t=27.0 μs

(c) t=34.4 μs

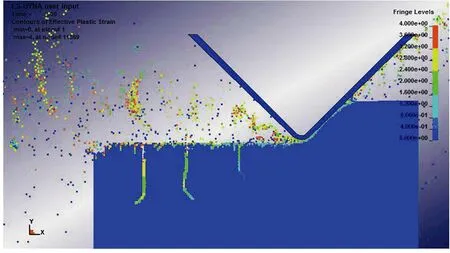
(d) t=40.0 μs

Fig.4 Simulation results of the subsurface crack formation process

由图4可见，工件材料亚表层裂纹的扩展过程大致分为3个阶段：1)裂纹起裂阶段. 在磨粒的挤压及撕扯作用下，工件基体上形成了垂直于工件表面的纵向微裂纹，当裂纹尖端处的应力超过材料的断裂强度后，微裂纹发生突进扩展，此时裂纹的贯通效果明显，材料内部有明显的裂纹产生(见图4(a)). 2)裂纹稳定扩展阶段. 随着磨粒的进一步切入，接触应力的累积增大使得裂纹持续向下扩展，而且这个阶段裂纹的扩展规律符合一般断裂力学公式的模拟规律(见图4(b)和(c)). 3)裂纹停裂阶段. 磨粒划过工件材料后，相应区域的应力逐渐减弱，当不满足裂纹扩展条件时裂纹停止扩展,见图4(d).

4 切削工艺参数优化

在磨料的制造过程中磨粒的形状很不规则，加工中磨料的破坏形式也具有很大的随机性. 单颗磨粒切削加工仿真研究中通常采用简单的几何体来模拟磨粒的形状，如圆锥体、球体、多棱锥体等[2]，且大多数磨粒都呈不规则的多棱锥形状，并存在一定的切削刃钝圆半径. 因此，本文使用锥角为90°的圆锥形金刚石压头对熔石英试件进行了系列刻划实验，经检测金刚石压头切削刃钝圆半径为0.5 μm. 刻划结束后对试件沿垂直于划痕方向逐层抛光、HF酸腐蚀和超声清洗，再用OLS3000激光共聚焦显微镜检测亚表层裂纹扩展深度，最终得到了在不同切削速度和切削深度下亚表层裂纹深度的变化曲线，见图5.

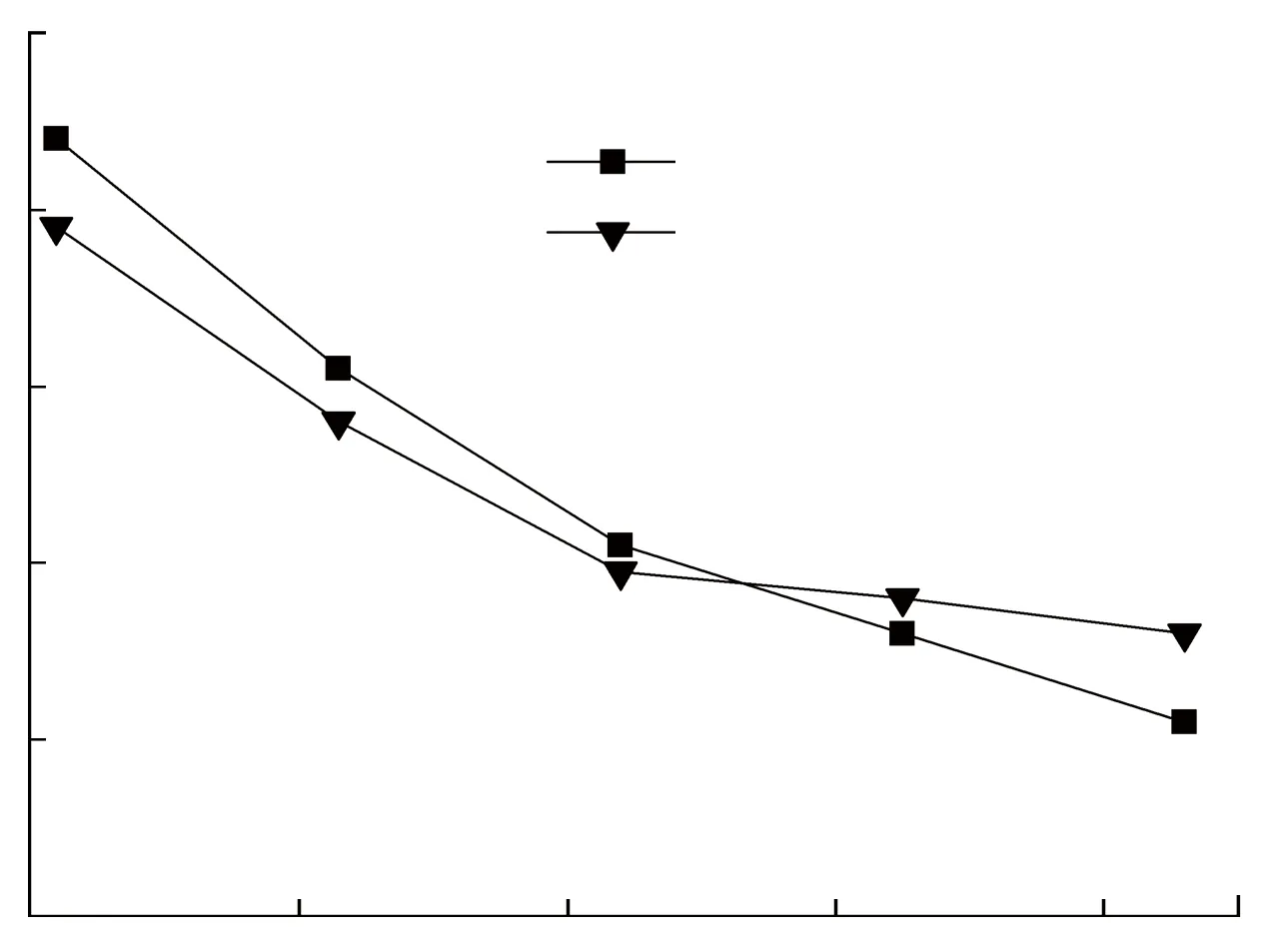
(a) 切削速度的影响

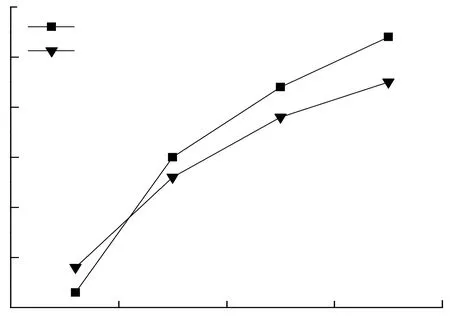
(b) 切削深度的影响

Fig.5 Effects of cutting speed and cutting depth on subsurface crack depth

仿真时采用的磨粒切削刃钝圆半径为0.5 μm,磨粒锐度角为90°,切削深度为1.5 μm，最终得到切削速度对亚表层裂纹深度(SSD)的影响规律如图5 (a))所示. 可以看出，随着磨粒切削速度的增大，亚表层裂纹深度呈递减趋势. 但是在实际加工中,过大的研磨速度会导致研磨液被甩出研磨区域，使单颗磨粒承受的载荷增大，反而会增大工件亚表层损伤深度，因此切削速度应该限制在一定的范围内. 仿真时采用的磨粒切削刃钝圆半径为0.5 μm,磨粒锐度角为90°，切削速度为1.05 m/s，得到切削深度对SSD的影响规律如图5(b))所示. 可以看出，随着切削深度的增加，亚表层裂纹扩展深度不断升高. 这是因为随着切削深度的增大，磨粒刀具与工件之间的挤压作用增强，导致磨粒的法向切削力增大，最终引起亚表层裂纹深度增加，而在切削深度足够小时可以实现脆性光学材料的延性域加工. 因此，在满足加工效率要求的前提下，应尽量选取较小的切削深度进行加工，以减小工件材料的亚表层裂纹深度.

选用90°和60°两种不同的磨粒锐度角，研究磨粒锐度角对亚表层裂纹扩展深度SSD的影响规律. 采用的其他切削参数为：切削速度为1.05 m/s，切削深度为1.5 μm. 仿真分析的结果如图6所示.

(a) α=90°

(b) α=60°

Fig.6 Simulation results of subsurface crack depths in different grain angle of sharpness

由图6可知，磨粒锐度角对光学元件研磨加工亚表层裂纹深度也有较大影响，随着磨粒锐度角的减小，磨粒对工件材料的挤压作用增强，使得接触区内的接触应力迅速增加，从而在材料内部诱发更为严重裂纹损伤，亚表层裂纹深度会急剧增大. 而当磨粒锐度角较小时，在磨粒初始切入的过程中容易导致工件边缘崩碎. 由此可见，为了减小加工后工件材料的亚表层损伤深度，在满足加工效率要求的前提下，应尽量选用较钝的磨粒.

5 结 论

1)基于光滑粒子流体动力学(SPH)法和JH-2材料本构模型，建立了熔石英材料单个磨粒切削加工过程的FE/SPH耦合有限元模型，并对熔石英材料单个磨粒切削加工过程进行了数值模拟.

2)分析了材料的脆性去除和亚表层裂纹的形成过程，提出了一种能够模拟脆性材料内部裂纹形成过程的有效仿真方法，并利用金刚石压头对熔石英试件进行了系列刻划实验，验证了FE/SPH耦合有限元仿真方法的正确性.

3)亚表层裂纹扩展深度与切削深度成正比关系，与切削速度成反比关系，并且磨粒锐度角对亚表层裂纹深度的影响也比较显著，故研磨加工宜采用较高的切削速度、较小的切削深度和比较钝的磨粒.

[1] GU W, YAO Z Q. Evaluation of surface cracking in micron and sub-micron scale scratch tests for optical glass BK7[J]. Journal of Mechanical Science and Technology, 2011, 25(5): 1167-1174. DOI:10.1007/S12206-011-0306-2.

[2] PETIT F, OTT C, CAMBIER F. Multiple scratch tests and surface-related fatigue properties of monolithic ceramics and soda lime glass [J]. Journal of the European Ceramic Society, 2009, 29(8): 1299-1307. DOI:10.1016/j.jeurceramsoc.2008.09.019.

[3] 吕东喜,王洪祥,唐永健,等. 旋转超声加工中磨粒冲击作用的仿真分析[J].哈尔滨工业大学学报,2013,45(1):682-687.

LV Dongxi，WANG Hongxiang，TANG Yongjian，et al. Simulation analysis on the impact effects of the abrasive in rotary ultrasonic machining process [J]. Journal of Harbin Institute of Technology,2013,45(1):682-687.

[4] 宿崇,侯俊铭,朱立达,等. 基于SPH 法的金属切削大变形数值模拟[J]. 东北大学学报,2009,30(3):418-421.

SU Chong, HOU Junming, ZHU Lida, et al. SPH-based numerical simulation for big deformation during metal cutting[J]. Journal of Northeastern University, 2009, 30(3):418-421.

[5] LIU G R,LIU M B. 光滑粒子流体动力学: 种无网格粒子法[M]. 韩旭译. 长沙:湖南大学出版社，2005.

LIU G R, LIU M B. Smoothed particle hydrodynamics: A non-mesh particle method[M].Changsha: Hunan University Press, 2005.

[6] FARAUD M，DESTEFANIS R，PALMIERI D, et al. SPH simulations of debris impacts using two different computer codes [J]. International Journal of Impact Engineering, 1999, 23(1):249-260. DOI:10.1016/S0734-743X(99)00077-9.

[7] CRONIN D S, BUI K, KAUFMANN C, et al. Implementation and validation of the Johnson-Holmquist ceramic material model in LS-DYNA [C]//4th European LS-dyna Users Conference.[S.l.]: Ulm, 2003:47-60.

[8] 吕东喜. 硬脆材料旋转超声加工高频振动效应的研究 [D].哈尔滨:哈尔滨工业大学, 2014.

LV Dongxi. High frequency vibration effects in rotary ultrasonic machining hard-brittle material [D]. Harbin: Harbin Institue of Technology, 2014.

[9] 江东亮. 无机非金属材料手册[M]. 北京:化学工业出版社, 2009.

JIANG Dongliang. Inorganic non-metallic materials Manual [M].Beijing: Chemical Industry Press, 2009.

[10]CHANG Y P, HASHIMURA M, DORNFELD D A. An investigation of material removal mechanisms in lapping with grain size transition [J]. Journal of Manufacturing Science and Engineering, 2000, 122(3): 413-419.

[11]BULSARA V H, AHN Y, CHANDRASEKAR S, et al. Mechanics of polishing [J]. Journal of applied mechanics, 1998, 65(2): 410-416.

[12]MALKIN S,HWANG T W. Grinding mechanisms for ceramics[J]. CIRP Annals-Manufacturing Technology，1996,45(2):569-580.

[13]DOMAN D A, BAUER R, WARKENTIN A. Experimentally validated finite element model of the rubbing and ploughing phases in scratch tests [J]. Journal of Engineering Manufacture,2009,223(12):1519-1527. DOI:10.1243/09544054JEM1520.

[14]沈琳燕,李蓓智,杨建国. 光学玻璃磨削机理的仿真研究 [J]. 制造技术与机床,2010 (2)：104-106.

SHEN Linyan, LI Beizhi, YANG Jianguo. Simulation study of optical glass grinding mechanism [J].Manufacturing Technology & Machining Tool, 2010(2):104-106.

[15]孟彬彬. 光学玻璃磨削裂纹形成过程仿真及试验研究[D]. 哈尔滨:哈尔滨工业大学, 2011.

MENG Binbin. Simulation and experimental research of cracks forming process in optical glass grinding[D]. Harbin: Harbin Institue of Technology, 2011.

(编辑 杨 波)

Numerical simulation of crack formation process in lapping fused silica optics

WANG Hongxiang, YAN Zhilong, WANG Jinghe, ZHOU Yan, BAI Hua, ZHAI Wenjie

(School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China)

The conventional finite element method is over-reliance on the mesh dimension, specifically, the mesh distortion is usually serious in the contact area of the abrasive particle and workpiece which makes it more difficult to simulate the formation process of internal cracks in brittle materials. To simulate the lapping process of fused silica optics, FE/SPH model of the machining process for a single abrasive particle was established. Then a new way to simulate the cutting process of brittle materials was provided. The formation process of subsurface crack and the influence of cutting parameters on subsurface damage depths were analyzed. Simulation results show that the brittle material is in the elastic-plastic deformation stage when abrasive particle is just beginning to cut into the workpiece，further amounts of microcracks arise under the extrusion and tear effects of the abrasive particle. The combination and extension of microcracks produced transverse and longitudinal cracks, which are parallel and perpendicular to the workpiece surface, respectively. Consequently, brittle-fracture removal of the workpiece material is completed.

fused silica optics；smoothed particle hydrodynamics；subsurface cracks；lapping；brittle materials

10.11918/j.issn.0367-6234.201603060

2016-03-11

国家自然科学基金(51475106, 51475119); 国防基础科研科学挑战专题(JCKY2016212A506-0503)

王洪祥(1967—)，男，教授，博士生导师； 翟文杰(1964—)，男，教授，博士生导师

王洪祥，whx@hit.edu.cn

TG580.692

A

0367-6234(2017)07-0052-05