基于CORS的区域电离层建模及其在PPP中的应用

范昆飞，黄名华，孔建

(1.南宁市国土测绘地理信息中心，广西 南宁 530021； 2.武汉大学，湖北 武汉 430079)

基于CORS的区域电离层建模及其在PPP中的应用

范昆飞1*，黄名华1，孔建2

(1.南宁市国土测绘地理信息中心，广西 南宁 530021； 2.武汉大学，湖北 武汉 430079)

利用CORS观测数据计算电离层延迟，采用低阶球谐函数建立实时区域电离层模型。对非差非组合PPP进行电离层约束，加快PPP收敛速度。与传统消电离层组合PPP相比，初始历元误差小于 0.5 m，E、N方向收敛速度提升显著，U方向有一定改善，定位精度提升了12.2%。

CORS；区域电离层模型；PPP；非差非组合

1 引 言

和传统的差分定位相比，精密单点定位(Precise Point Positioning)在进行定位服务时只需要一个接收机以及IGS(International GPS Service)发布的精密轨道数据和钟差数据，操作方式简便快捷，广泛应用于交通导航等领域。目前在实时PPP中，收敛速度是制约其在实际中应用的重要问题[1，2]。电离层延迟是GPS定位中重要的误差源。传统无电离层组合虽然能够基本消除电离层的影响，在收敛后能够获得理想的定位精度，但是观测值组合会放大伪距的噪声，使得PPP的收敛速度较慢。非差非组合PPP在改正电离层延迟时通常使用KLOBUCHAR模型、IGS发布的全球电离层地图(Global Ionosphere Map，GIM)等。但是KLOBUCHAR模型为经验模型，与实际电离层情况相差较大，改正效果不理想；GIM产品发布通常要之后2天～3天，无法实现实时PPP[3～5]。我国目前所有省市已经完成或正在建立高精度的CORS系统，利用区域较高密度的连续GPS跟踪站能够建立高精度、高时空分辨率的区域电离层模型，为实时PPP提供准确的电离层延迟产品，提高实时PPP的收敛速度和精度。

本文利用载波相位平滑伪距提取CORS测站电离层延迟，然后采用球谐函数拟合区域电离层模型。根据区域电离层模型对实时流动站PPP进行电离层改正，检验区域电离层模型对PPP收敛速度和定位精度的影响。

2 非差非组合PPP

传统消电离层组合PPP算法是将GPS双频信号中的伪距和载波观测值组合来消除电离层延迟的一阶项，忽略了电离层延迟的高阶项。但是该组合会放大伪距和载波的观测值噪声[6]。非差非组合PPP算法将各个卫星信号路径上的电离层延迟作为待估参数，不进行观测值之间的组合。非差非组合PPP伪距和载波观测方程为：

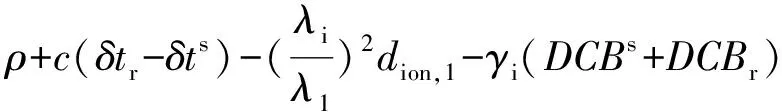
(1)

(2)

其中，P、L分别为GPS信号中伪距和载波观测值；ρ为卫星和接收机之间的真实几何距离；c为真空光速；δts、δtr分别代表卫星和接收机钟差；ρion为电离层延迟，γi为伪距DCB系数，DCBs、DCBr分别为卫星和接收机硬件延迟，λ、N分别表示载波波长和整周模糊度；△为其他误差改正，包括对流层延迟、天线相位中心偏差、地球自转、相对论等；εP、εL分别代表伪距和载波观测噪声。

3 基于CORS的区域电离层建模

GPS信号的电离层延迟与信号频率的平方成反比，因此可以利用GPS双频信号计算GPS信号传播路径上的电离层延迟[7]。目前利用GPS观测数据计算电离层延迟的方法主要有相位观测值法、伪距观测值法、相位平滑伪距观测值法以及非差非组合PPP法。相位观测值法由于存在整周模糊度问题，只能确定相对电离层延迟，而伪距观测值法噪声较大，精度较差。非差非组合PPP法依赖于事后的高精度卫星轨道产品和钟差产品，难以满足实时处理的需求[8]。目前国际上通用的方法为载波相位平滑伪距法，该方法能够获得较高精度的电离层延迟，具体观测方程为：

(3)

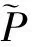
(4)

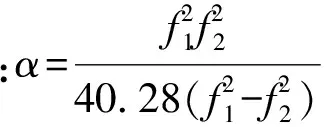
(5)

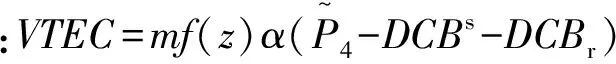
(6)

本文选择低阶球谐函数对区域电离层进行建模

(7)

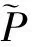
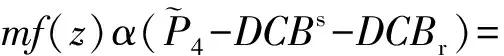
(8)

由上式可以同时对区域电离层球谐函数和卫星、接收机硬件延迟进行求解。为了分离卫星和接收机硬件延迟，增加卫星硬件延迟的重心基准，即：

(9)

其中：Sn为卫星总数。

4 精度验证

本文采用某市的高精度CORS网络观测数据，选取其中A站作为流动站，其余站作为参考站，利用参考站观测数据计算区域电离层模型，如图1所示。然后IGS提供的实时星历、钟差产品，分别采用传统无电离层组合、非差非组合加电离层约束两种方法计算流动站坐标，与已知坐标进行对比，检验定位结角形为周围的参考站，为PPP计算提供观测数据计算区域电离层模型。

图1 流动站和参考站位置分布

4.1 区域电离层模型

根据前面第3部分区域电离层模型建模方法，利用参考站观测数据建立了单层的电离层模型，图2给出了初始时间段(0 min～30 min)的建模结果。从图中可以看出，在初始时间段内，电离层并不平静，在北部区域电离层浓度较低，在25～27TECU左右，而在东南部出现了峰值区域，峰值约为37左右。区域电离层模型整体较为平滑，密度值受X方向位置影响较大。

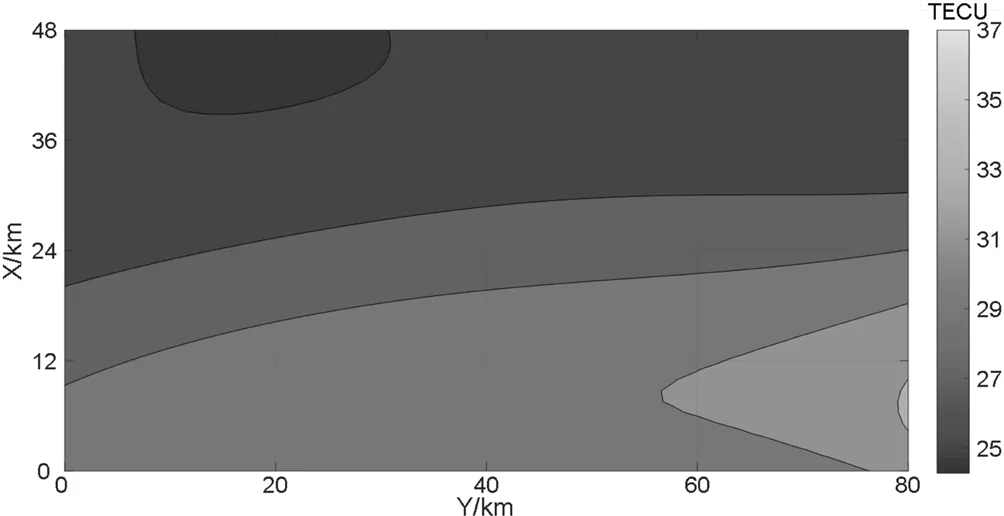
图2 初始时段区域电离层模型

4.2 PPP定位精度

将4.1中区域电离层建模结果作为方程的约束条件带入计算过程，获得非差非组合加电离层约束PPP的定位结果。图3和图4分别给出了传统无电离层组合PPP和非差非组合加电离层约束PPP定位结果。

图3 传统无电离层组合PPP定位结果

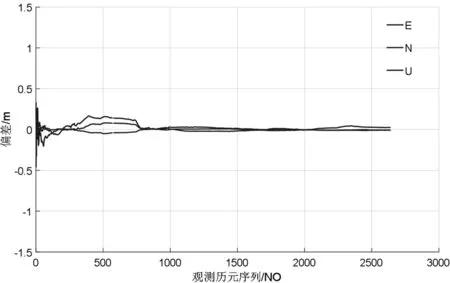
图4 非差非组合加电离层约束PPP定位结果

从图3中可以看出，传统无电离层组合定位结果中E、N、U三个方向的初始历元的定位误差都非常大，其中N方向和U方向的误差达到了 1.5 m。E方向收敛时间为 31 min，N方向为 10 min，U方向为 46 min。

图4给出了非差非组合加电离层约束PPP的定位结果，从图中可以看出，该方法的初始历元的定位误差较小，其中E方向误差为 -0.46 m，N方向为 0.25 m，U方向为 0.33 m，初始历元定位结果即可满足一般交通导航等应用。随着时间推移，三个方向定位结果不断收敛，其中E方向收敛时间为 7 min，N方向为 7 min，U方向为 42 min。与传统无电离层组合PPP定位结果相比，E方向和N方向收敛速度有显著提升，U方向收敛速度也有一定改善。在300～800观测历元时间段内，两种定位方法结果都有一定的扰动，其中U方向变化最大，可能是短时间的对流层变化引起的。

表1给出了传统无电离层组合PPP和非差非组合加电离层约束PPP的收敛时间和定位精度统计。从表中可以看出，非差非组合加电离层约束PPP收敛速度相比于传统消电离层组合方法有了显著提升，尤其是E、N方向，分别提升了77.4%和百分之30%，U方向也有改善，提升了约8.6%。在定位精度方面，非差非组合加电离层约束PPP方法也有改善，E、N、U方向分别提升了22.5%、11.9%、7.8%，综合定位精度为 6.19 cm，相比传统无电离层组合提升了约12.2%。

收敛时间和定位精度统计 表1

5 结 论

实时精密单点定位中，电离层误差是影响其收敛时间的重要误差源。传统消电离层组合PPP虽然能够消去电离层误差，但是会放大伪距中的噪声，定位结果并不理想。本文利用高精度的CORS系统作为参考系统，利用其观测数据建立区域电离层模型，在非差非组合PPP中将电离层延迟作为已知项，对方程进行约束，加快收敛速度和提高定位精度。

实际流动站定位实验结果表明，非差非组合PPP加电离层约束方法初始历元精度较高，误差在 0.5 m以内。E、N方向收敛时间小于 10 min，相比于消电离层组合PPP，收敛速度分别提升了77.4%和30%，U方向也有一定改善。定位精度方面，非差非组合加电离层约束PPP方法定位精度为 6.19 cm，相比于消电离层组合PPP提升了12.2%。基于CORS区域电离层建模产品增强的非差非组合PPP能够显著缩短精密单点定位的收敛速度，随着我国各省CORS的建立和融合，该方法具有广泛的应用前景。

[1] 姜卫平，邹璇，唐卫明. 基于CORS网络的单频GPS实时精密单点定位新方法[J]. 地球物理学报，2012，55(5)：1549～1556.

[2] 张瑞，姚宜斌，郑艳丽. 基于区域电离层建模的单点定位应用分析[J]. 大地测量与地球动力学，2013，33(1)：69～73.[3] 张宝成. GNSS 非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报，2014，43(10)：1099～1099.

[4] 闫伟，袁运斌，欧吉坤等. 非组合精密单点定位算法精密授时的可行性研究 [J]. 武汉大学学报：信息科学版，2011，36(6)：648～651.

[5] 许承权，花向红，范千等. 基于神经网络的区域电离层模型及其在单频 PPP 中的应用[J]. 测绘工程，2009，18(4)：1～6.

[6] 李征航，黄劲松. GPS测量与数据处理[M]. 武汉：武汉大学出版社，2005，102～105.

[7] 刘经南，陈俊勇，张燕平等. 广域差分GPS原理和方法[M]. 北京：测绘出版社，1999.

[8] 袁运斌.基于GPS的电离层监测及延迟改正理论与方法的研究[D]. 武汉：中国科学院测量与地球物理研究所，2002.[9] 章红平，高周正，牛小骥等. GPS非差非组合精密单点定位算法研究[J]. 武汉大学学报：信息科学版，2013，38(12)：1396～1399.

Regional Ionospheric Modeling Based on CORS and Its Application in PPP

Fan Kunfei1，Huang Minghua1，Kong Jian2

(1.Nanning Land Surveying and Mapping Geographic Information Center，Nanning 530021，China； 2.Wuhan University，Wuhan 430079，China)

Using the CORS observation data to calculate the ionospheric delay，the real time regional ionosphere model is established by using the low order spherical harmonic function. The convergence rate of un-differential and un-combined PPP is accelerated by the ionospheric constraint. Compared with the traditional ionosphere free PPP，the initial epoch error less than 0.5 m，E，N direction convergence speed significantly improved，and the U direction has a certain improvement，positioning accuracy increased 12.2%.

CORS；regional ionospheric model；PPP；un-differential and un-combined

1672-8262(2017)03-75-04

P228

B

2016—11—18

范昆飞(1986—)，男，工程师，主要研究方向为CORS维护与应用。

南宁市第三批特聘专家科研项目；南宁市人才小高地资助项目。