基于SWAN模式的“灿鸿”台风浪数值模拟

应王敏, 郑 桥, 朱陈陈, 朱 业, 车助镁, 楚栋栋, 张继才

(1. 浙江大学 海洋学院 物理海洋研究所, 浙江 舟山 316000; 2. 浙江省海洋监测预报中心, 浙江 杭州310000)

基于SWAN模式的“灿鸿”台风浪数值模拟

应王敏1, 郑 桥1, 朱陈陈1, 朱 业2, 车助镁2, 楚栋栋1, 张继才1

(1. 浙江大学 海洋学院 物理海洋研究所, 浙江 舟山 316000; 2. 浙江省海洋监测预报中心, 浙江 杭州310000)

以第三代海浪模式SWAN(simulating wave nearshore, 近岸海浪数值模型)为基础, 构建了东中国海海域波浪数值模式, 并以高时间、空间分辨率的CCMP(cross calibrated multi-platform, 多平台交叉校正)风场作为驱动风场进行波浪计算, 模拟了1509号“灿鸿”台风的波浪过程。同时, 对SWAN模式中的底摩擦参数化方案、波浪破碎参数、风能输入与白冠耗散、波-波非线性相互作用等因素对台风浪模拟的影响进行了分析, 并对模式中的各影响因素给出了建议。模拟结果与浮标实测有效浪高数据(舟山朱家尖站、南麂岛站、舟山外海站、温州外海站)两者之间的偏差较小, 表明本研究所建立的模式以及选择的参数合理, SWAN和CCMP风场的结合能满足海洋波浪数值模拟的需求。本研究对于台风浪数值预报具有参考意义。

第三代海浪模式SWAN(simulating wave nearshore); CCMP(cross calibrated multi-platform)风场;台风浪; 东中国海; “灿鸿”台风

我国沿海海岸线较长, 经常受到不同程度波浪的影响, 其中台风浪对我国沿海区域的工程实施和居民生活造成了巨大的危害。波浪数值模拟已经成为研究波浪的不可或缺的工具, Mile[1]和Phillips[2]提出波浪成长机制理论, 由此诞生了第一代海浪数值模式。发现波与波之间的非线性相互作用在能量转化的过程中起着非常重要的作用后[3], 在第二代海浪数值模式中加入了非线性作用项的影响。现今以WAM(wind wave model)、WWIII(wavewatch-III)和SWAN(simulating wave nearshor, 近岸海浪数值模型)为代表的第三代海浪模式在波浪场预报中得到了很大的应用[4], 其中SWAN模型在近岸海浪模拟中具有较好的模拟精度。Booij等[5]将SWAN模式的计算结果与线性理论及现场实测资料进行对比, 表明SWAN能够准确模拟潮流、地形、风场环境下的波浪场, 适用于风浪、涌浪和混合浪的预报。

在台风所致波浪场的模拟中, 风场资料的准确性直接影响台风浪的模拟结果, 因此可靠准确的风场资料是台风波浪场模拟的必要条件。在目前的台风波浪场模拟中, 不少学者采用高分辨率的CCMP (cross calibrated multi-platform, 多平台交叉校正)风场资料, 取得了合理的模拟结果, 如谭凤等[6]结合WRF风场和SWAN模式对“韦帕”台风波浪场进行模拟, 获得较好的实验结果; 张鹏等[7]利用CCMP卫星遥感风场驱动SWAN模式, 其模拟结果与渤海浮标站点资料有很好的一致性。

“灿鸿”(CHAN-HOM)是2015年登陆我国东南沿海的超强台风, 登陆时中心最大风力14级, 最大风速45 m/s, 海浪高度达4～8 m, 引起海浪和台风风暴潮红色警报的同时发布。本文使用SWAN海浪模式,以“灿鸿”台风过程为例对台风浪进行了数值模拟,并以CCMP风场作为驱动风场对影响东海海域台风浪计算的各因素进行了分析和探讨, 给出了较为合理的模型参数, 使得SWAN模式在东海台风浪计算中更具适用性。据文献调研, 暂无学者对“灿鸿”台风所导致的波浪过程进行数值模拟, 本文对该台风过程的模拟可为后续类似台风浪的模拟提供参考依据。

1 SWAN海浪模型简介

1.1 大气模式CCMP

CCMP海面风场由NASA在2009年推出的全球表面风场同化资料, 采用了一种增强的变分同化分析方法, 结合了诸多海洋被动微波和散射计遥感平台上采集的海面风场数据。CCMP风场具有较高的精度和时空分辨率: 时间分辨率6 h, 空间分辨率为0.25°×0.25°, 空间范围78.375°S—78.375°N, 0.125°—359.875°E。Atlas等[8]通过实验证实了CCMP数据较其他单个卫星平台测量的风场数据在精度方面有很大的提高, 能够满足海洋和大气研究的需要。本文使用的CCMP风场来自网站http: //www.remss.com/measurements/ ccmp, 选用时间段为2015-06-28—2015-07-16, 利用Matlab处理netCDF4格式, 提取研究区域的经纬度信息及具体风速, 并将其处理拼接成SWAN模式所要求的风场格式。

1.2 SWAN海浪模式

SWAN模型是由Delft大学土木工程系采用基于Euler近似的作用量谱平衡方程和线性随机表面重力波理论开发的第三代浅海海浪数值模式。SWAN模式采用基于能量守恒原理的平衡方程, 除了考虑第三代海浪模式共有的特点, 还充分考虑了模式在浅水模拟的各种需要。

1.2.1 控制方程

SWAN模型以作用量密度N(N=E/σ, σ为相对频率)建立平衡方程[9]:

方程左边第一项表示作用量密度随时间的变化率。第二项和第三项表示作用量密度在几何空间的传播(变化率Cx和Cy)。第四项表示由流和水深变化引起的折射和变浅作用(Cσ)。第五项表示流和水深变浅引起的频移(Cθ), 方程右边的S表示能量源项。

1.2.2 SWAN的数值方法

作用量平衡方程中, 每一格点的状态由迎浪格点状态决定。因此, 最有效的差分方法就是隐式迎风格式, 无条件稳定, 可以使用比较大的时间步计算(在浅水中比显式大得多)。对二阶HISWA浅水波模型的研究表明, 在近岸区域一阶迎风差分格式具有较高的精度。在谱空间补充二阶中心差分后, 可以满足精度上的要求。SWAN在时间和空间采用隐式迎风差分格式, 在谱空间使用中心差分格式。SWAN允许将谱空间四等分, 除了两者之间的折射和非线性波-波作用引起的相互作用之外, 这些等分的计算可以分别进行。

2 模型设置

2.1 计算区域及计算条件设置

本文计算区域为东中国海, 范围11°—43°N, 114°—134°E。模拟海域内, 最大水深约6 000 m, 最小水深约11 m, 采用单层三角网格, 图1为研究区域的水深分布和网格示意图。

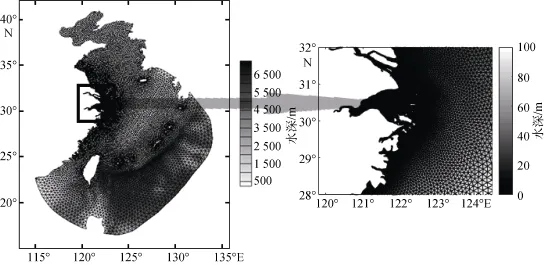
图1 研究海域水深及模式计算网格示意图及浙江近岸局部放大后的计算网格图Fig. 1 Water depth in study area; model’s computation grids and enlarged view for Zhejiang coastal area

计算区域内东边界和南边界是开边界, 计算采用的时间步长为20 min, 离散频率范围设置在0.040 0～ 1.000 0 Hz。为了提高模拟的准确度, 计算网格在浙江沿海海域进行了加密, 从外海开边界区域到陆域岸线区域, 空间步长从50 km逐渐过渡到1 km。在进行单一因素研究时, 其他参数如风输入、白浪耗散、底摩擦、以及浅水破碎指标等均采用SWAN默认设置。

图2为浮标观测站点分布图, 分别是舟山朱家尖站(ZJJ, 29.894°N, 122.427°E, 水深9.08 m)、南麂岛站(NJD, 27.459°N, 121.082°E, 水深21.26 m)、舟山外海站(ZSWH, 29.500°N, 123.965°E, 水深69.44 m)以及温州外海站(WZWH, 27.500°N, 122.500°E, 水深91.44 m)。图3给出了南麂岛站和舟山外海站实测风速以及CCMP风速(朱家尖站、温州外海站观测数据缺失严重), 其中CCMP风速是利用CCMP数据线性插值到观测站点得到的。可以发现, CCMP风场数据与观测站点数据在变化趋势上基本一致, 数值符合性较好, 故利用CCMP数据作为本文波浪模型的驱动是合理的。

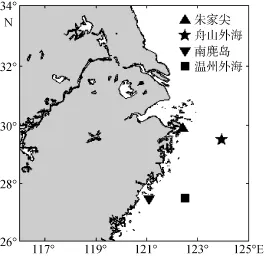
图2 观测站点地理位置图Fig. 2 Location of observation stations

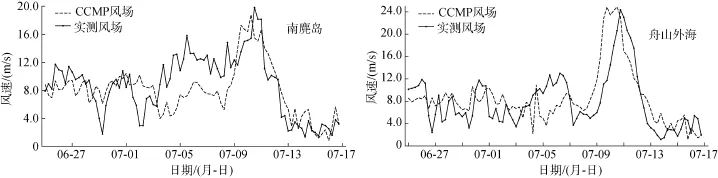
图3 实测风速和CCMP风速变化对比图Fig. 3 Comparison between in-situ wind speed observations and interpolated CCMP wind speed

2.2 预实验

在进行数值模拟前, 首先要确定风场输入的提前时间长短, 以及冷热启动方式对实验结果的影响。为此本文进行了两个预实验, 最终确定模式输入时风场提前时间总计5 d, 包含冷启动预热3 d、风场预热2 d。

2.2.1 研究风场预热时间对模拟结果的影响

为了研究风场预热时间对实验结果的影响, 风场数据分别提前1、2和5 d, 其他控制参数均采用默认设置, 地形输入条件相同。以朱家尖站为例, 利用SWAN模型进行分析计算。为了书写方便, 三组实验分别记为A1、A2和A5。

由表1可知, A1与A5及A2与A5的模拟结果的相对误差均没有超过1%。因此风场的预热天数对模拟结果影响不大, 即模拟结果对风场启动时间不敏感。最终本文试验风场的预热天数选为两天。

2.2.2 研究冷、热启动对实验结果的影响

冷启动的特点是每次海浪高度从零开始计算,不足之处是海浪初始模拟值是不准确的。为提高计算效率, 需要研究初始不稳定的时长, 以此来确定最为高效的启动时间。采用东海预报中心(热启动)SWAN模拟的数据进行对比, 其他参数(如风场类型、水深、地形、模式参数等)保持不变, 采用冷启动的方式进行平行实验, 模拟时间为2016-05-12—2016-05-16, 其模拟结果如图4所示。

计算结果表明, 冷热起动造成的差异基本上在海浪起动阶段, 差异期为三天。三天后冷、热启动两种方式对实验结果的差异基本消除。下文的数值实验皆采用冷启动方式, 启动后三天的模拟结果用于分析。

3 模式参数选择

除输入的风场数据外, 影响SWAN模式风浪模拟准确性的因素众多, 因此有必要对各种影响因素进行分析, 使模拟结果更加准确。选取2015-06-30—2015-07-16台风期间的南麂岛站(水深21.26 m)和朱家尖站(水深9.08 m)进行分析, 分别对底摩擦参数、波浪破碎参数、波浪非线性相互作用模式等因素进行了研究; 并依据敏感性分析的结论, 优化敏感参数, 获取适用于“灿鸿”台风浪的最优参数值。

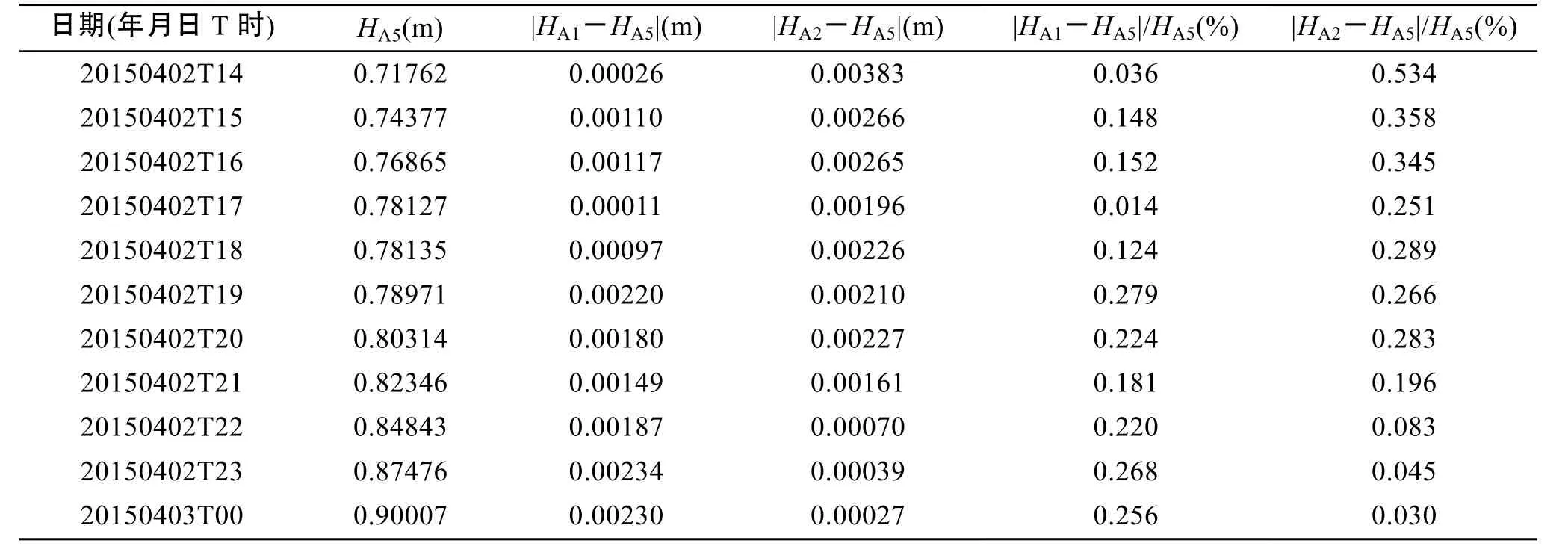
表1 三组实验波高模拟结果差异分析Tab. 1 Differences between simulation results of wave height in three experiments

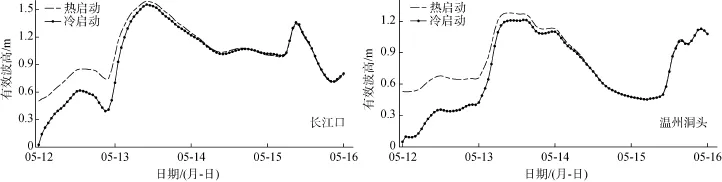
图4 冷、热启动波高变化对比实验Fig. 4 Comparison between simulation results using hot and cold starts

3.1 底摩擦参数对模拟结果的影响

底摩擦过程造成的能量耗散, 对于波浪的传播起着重要的作用。摩擦力的强度[11]取决于海底条件以及水质点随波浪的轨迹速度。SWAN模式中底摩擦耗散有三种计算方式: JONSWAP(经验性模式)、COLLINS(拖曳模式)、MADSEN(涡黏模式), 分别由Hasselmann[12]、Collins[5]、Madsen提出。图5和图6分别展示了三种方案在南麂岛站和朱家尖站的海浪模拟结果, 三种方案底摩擦参数的缺省值分别为0.067、0.015、0.050。

由此可见, 三种底摩擦方案模拟出的波高变化趋势相似, 在波高较小的阶段数值差异不大。在台风登陆时期, MADSEN模式的模拟波高明显低于JONSWAP模式和COLLINS模式, 后两者较接近观测数据。台风高浪期间, 不同底摩擦模式之间的差异幅度和水深密切相关, 差异性在深度较浅的朱家尖站比南麂岛站小。

为了进一步研究三种方式中底摩擦系数对实验结果的影响, 以缺省值为中心, 上下浮动25%变化。由于系数变化对比实验在波高较低时差异不明显,仅截取2015-07-09—2015-07-13时段进行对比探讨。(1)JONSWAP模式底摩擦系数Cbottom变化范围为0.038～0.088, 梯度为0.010。对比结果表明, 随着底摩擦系数的增加, 波高模拟值减小, 在波高较大区域差异较为明显。(2)COLLINS模式底摩擦系数Cf变化范围为0.012～0.019, 梯度为0.001, 其结果与JONSWAP模式相似, 但波高变化幅度不如后者。(3)MADSEN模式底摩擦系数变化范围为0.042～0.066, 梯度设置0.004。系数的改变对波浪高度的影响较小, 且其模拟出来的结果误差相对较大。(4)综合比较发现, 底摩擦参数变化后对模拟结果的影响,在朱家尖站小于南麂岛站。

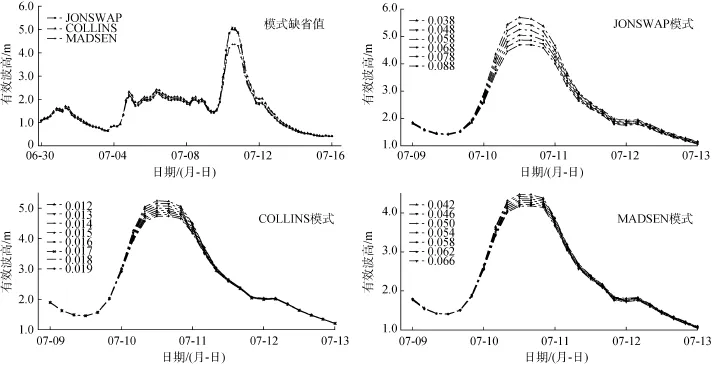
图5 三种底摩擦模式的对比图——以南麂岛站为例Fig. 5 Comparison between use of three methods for bottom friction parameterization; selected station is NJD

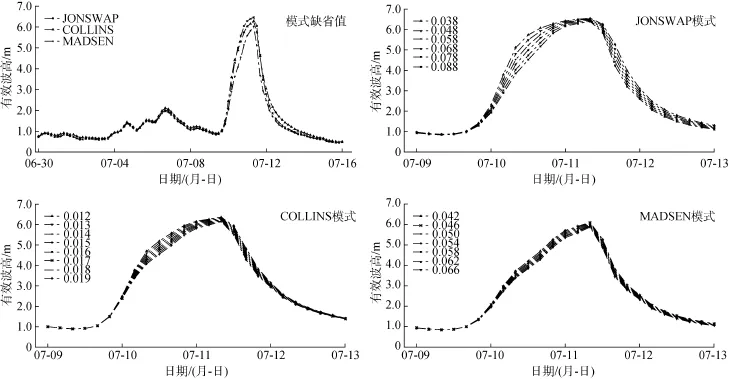
图6 三种底摩擦模式的对比图——以朱家尖站为例Fig. 6 Comparison between use of three methods for bottom friction parameterization; selected station is ZJJ

3.2 浅化引起的波浪破碎对实验结果的影响

SWAN模式共考虑了三种类型的耗散机制: 在深水情况, 风浪的白冠破碎占主要地位, 控制着谱的高频部分的饱和程度; 在中等深度和浅水情况下,底摩擦变得重要; 但当波浪传到浅水破碎带附近时,水深变浅引起的波浪破碎占主要地位。Battjes和Janssen[14]分析了一系列实验室和现场试验的波浪数据, 发现在不同的地形类型下(平缓、沙槽、沙洲), 波浪破碎在0.6～0.83之间变化, 平均值为0.73。Kaminsky和Kraus[15]分析大量实验数据后得出结论, 破碎参数在0.6～1.59之间变化, 平均值0.79。

根据Kaminsky和Kraus[15]结论, 设置破碎参数在0.6～1.6之间变化, 梯度为0.2, SWAN模式缺省值为0.73。图7展示了波浪破碎系数对模拟波高的影响。实验结果表明, 在南麂岛站其影响非常小,但在朱家尖站则对此较为敏感。由此可知, 波浪破碎参数系数对模拟结果的影响与水深密切相关, 在浅水地区影响较大, 这是由其所代表的物理过程所决定的。

图7 浅化引起的波浪破碎系数影响Fig. 7 Effects of parameter of depth-induced wave breaking

3.3 风输入指数增长、白冠破碎项能量耗散的影响

SWAN海浪模式中, 采用的是第三代(GEN3)风输入指数增长、白冠破碎项能量耗散模式。SWAN中GEN3模式有三种常用的风输入指数增长和白冠破碎项能量耗散的参数化方案[16]: 默认设置的Komen方案、Janssen方案和Westhuysen方案。Komen方案和Janssen方案直接来源于第三代海浪模式WAM, 在早期版本的SWAN模式中已经广泛应用, Westhuysen方案则是在2007年由Westhuysen通过修改模式中已有的参数化方案而得到。针对风输入项和白浪破碎项分别采用了该三种方案, 各个物理过程的参数均采用预设值, 探究GEN3三种方案对实验结果的影响(图8)。

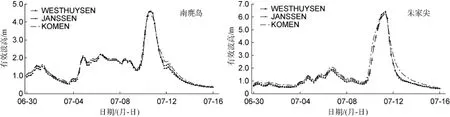
图8 风输入指数增长、白浪破碎项能量耗散参数影响Fig. 8 Effect of wind field exponential growth and white-capping caps breaking parameters

由此可见, Komen、Janssen、Westhuysen三种方案随着计算时间的延长, 模拟出来的波高值依次减小, 但三者之间的差异很小。此外, 随着水深的变化也未有明显差异。总体来说, 在本文设计的数值实验中, 实验结果对这个参数不敏感。

3.4 波-波非线性相互作用对实验结果的影响

波-波非线性相互作用是指共振波分量之间交换能量, 使能量重新分配, 在深海情况四波相互作用比较重要, 而在浅水情况三波相互作用较为重要。通过四波相互作用, 能量从高频率部分转向低频部分, 对于维持谱形和决定能量的方向分布起着重要的作用, 四波传播率在水深变浅时变小。在浅水情况, 当波陡较大时, 能量通过三波相互作用从低频部分向高频部分转移, 在临近岸边时, 单波峰的谱转变为多波峰的谱[18]。图9是非线性相互作用影响的数值结果, 其中Triad表示三波非线性相互作用, Limiter表示四波非线性相互作用。结果表明在波高较小时段, 实验结果对非线性相互作用不敏感; 但在波高因台风变大时, 两者的差异开始体现, 且在朱家尖站和南麂岛站敏感性较为接近。

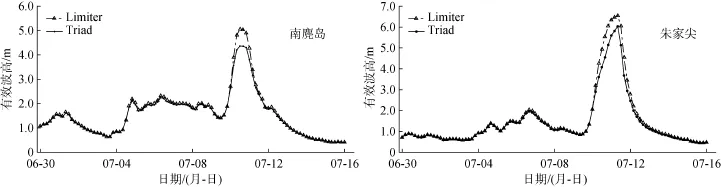
图9 非线性波波相互作用影响Fig. 9 Effects of non-linear wave-wave interactions

4 “灿鸿”台风浪模拟

“灿鸿”(CHAN-HOM)是2015年登陆我国东南沿海的超强台风, 于2015-06-30在西北太平洋洋面生成, 2015-07-11T16在我国浙江舟山朱家尖登陆。基于SWAN模式, 结合CCMP风场, 采取较优的参数方案, 本章模拟了“灿鸿”所引起的波浪场变化,并将模拟结果与浮标观测数据进行了对比。

4.1 模拟结果与观测结果的对比

图10展示了四个观测站模拟数据和实测数据,采用CCMP风场的模拟结果与浮标观测数据之间的偏差较小。尤其在台风来袭之际, CCMP风场的模拟数据的上升和下降趋势与观测数据吻合程度非常高。

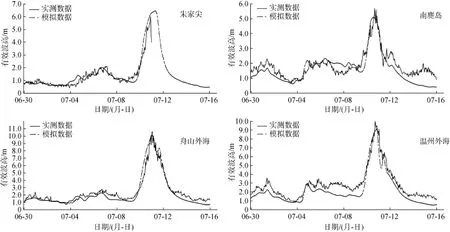
图10 观测站点波高模拟、实测对比图Fig. 10 Differences between simulation results and observations at four stations

选取舟山外海站波高变化图进行具体分析。如图所示, 在2015-06-30—2015-07-09期间, 舟山外海的波浪高度未出现异常变化, 处于0.9～2.5 m之间;从2015-07-09开始, 海域受到台风影响, 波浪高度开始快速上升, 至2015-07-11凌晨达到峰值10.5 m;而后波浪高度开始下降, 到2015-07-13恢复正常波高水平。根据CCMP风场模拟数据, CCMP风场的模拟波高与浮标实测数据十分接近, 上升趋势一致,峰值点几乎重合, 下降趋势也十分接近。

误差统计方面, 通过CCMP风场模拟出四个观测点的平均绝对误差为0.227、0.441、0.433、0.699 m,平均相对误差分别为: 18.04%、26.90%、20.19%、28.63%。从图中可以看出, 较大的误差多发生于波高从小变大或者从大变小的过渡时段。

4.2 台风过程中的波浪场分析

在台风“灿鸿”活跃期间, 朱家尖、南麂岛、舟山外海、温州外海的波浪均在2015-07-10—2015-07-11期间出现了有效波高的峰值。观测站点的波高前期尽管在波动变化, 但总体波高在0.5～3.5 m间。台风过境时段, 波高值与无台风时相比高出了4～5倍, 与台风带来的大风浪事实相符。

图11展示了通过CCMP风场资料模拟计算得到的中国近海海域有效波高分布, 限于篇幅, 仅选取了2015-07-10—2015-07-12的海域波高分布图。

总体来说, 研究区域内的有效波高随着台风“灿鸿”的逼近逐渐变高。由2015-07-10T00的海域有效波高图可知, 有效波高的最大值已经超过9 m, 但绝大部分海域并未掀起巨浪。而2015-07-10T12的研究海域内几乎全部已经处于一个巨浪的状态, 浙江近海区域的波高因台风登陆在2015-07-10和2015-07- 11达到峰值而后研究海域的波高逐渐减小并恢复正常。从图中可以发现: 有效波高的分布和台风路径有着密切的相关性。因为本文所采用的观测数据都处于浙江东南海域,台风的移动速度较快, 影响到观测站点附近的海域时,四个站点的波浪变化呈现出四点均一的现象。

5 结论与展望

本文以CCMP数据作为驱动风场, 采用SWAN模式模拟了“灿鸿”台风所导致(2015-06-30—2015-07-16)的波高变化, 并与观测站点浮标实测数据进行了对比分析。模拟结果表明: CCMP风场能够较好地模拟“灿鸿”台风浪过程, 计算结果与朱家尖、南麂岛、舟山外海、温州外海四个站点的浮标实测数据有较好的一致性, 模拟出的波高场较为合理地体现了台风所导致的波浪场。

此外, 本文还研究了底摩擦参数化方案和取值、波浪破碎参数、非线性相互作用等因素对海浪模拟的影响, 进行了多参数敏感性分析, 加深了对此模式参数的认识, 有助于对模式参数进行优化和调整。

下一步工作将构建以浙江近海为研究区域的波浪模式, 充分考虑岛屿、岸线和水深的空间分布状况, 提升网格空间分辨率, 进一步提升模拟和预报的效果。

[1] Miles J W. On the generation of surface waves by shear flows[J]. Journal of Fluid Mechanics, 1957, 3(2): 185-204.

[2] Phillips O M. On the generation of waves by turbulent wind[J]. Journal of Fluid Mechanics, 1957, 2(5): 417-445.

[3] 尹洪强. 基于SWAN模式下南海台风浪的推算[D].大连: 大连理工大学, 2014. Yin Hongqiang. Typhoon wave forecast in the South Sea by SWAN Model[D]. Dalian: Dalian University of Technology.2014.

[4] 杨洋. 西北太平洋台风浪后报[D]. 上海: 上海交通大学, 2009. Yang yang. Numerical simulation of typhoon waves in Northwest Pacific Ocean[D]. Shanghai: Shanghai Jiao Tong University, 2009.

[5] Booij N, Ris R C, Holthuijsen L H. A third-generation wave model for coastal regions. Part I. Model description and validation[J]. Geophys Res, 1999, 104(c4): 7649-7666.

[6] 谭凤, 张庆河, 庞启秀, 等. 基于WRF-SWAN模式的韦帕台风波浪场模拟[J]. 水道港口, 2012, 33(1): 14-18. Tan Feng, Zhang Qinghe, Pang Qixiu, et al. Numerical simulation of WIPHA typhoon waves using WRF-SWAN model [J]. Journal of Waterway and Harbor, 2012, 33(1): 14-18.

[7] 张鹏, 陈晓玲, 陆建忠, 等. 基于CCMP卫星遥感海面风场数据的渤海风浪模拟研究[J]. 海洋通报, 2011, 30(3): 266-271. Zhang Peng, Chen Xiaoling, Lu Jianzhong, et al. Research on wave simulation of Bohai Sea based on the CCMP remotely sensed sea winds [J]. Marine Science Bulletin, 2011, 30(3): 266-271.

[8] Atlas R, Ardizzone J, Hoffman R N. Application of satellite surface wind data to ocean wind analysis[J]. The International Society for Optical Engineering, 2008, 85(1): 92-103.

[9] 徐福敏, 张长宽, 陶建峰. 浅水波浪数值模型SWAN的原理及应用综述[J]. 水科学进展, 2004, 15(4): 538-542. Xu Fumin, Zhang Changkuan, Tao Jianfeng. Mechanism and application of a third generation wave model SWAN for shallow water [J]. Advances in Water Science, 2004, 15(4): 538-542.

[10] 王道龙. 近岸海浪模式研究[D]. 青岛: 国家海洋局第一海洋研究所, 2009. Wang Daolong. The research of coastal wave model[D]. Qingdao: The First Institute of Oceanography, State Oceanic Administration, 2009.

[11] 王道龙, 华锋, 江志辉. SWAN近岸海浪模式在辽东湾的应用[J]. 海洋科学进展, 2010, 28(3): 285-291. Wang Daolong, Hua Feng, Jiang Zhihui. Application ofcoastal wave model SWAN to Liaodong Bay[J]. Advances in Marine Science, 2010, 28(3): 285-291.

[12] Hasselmannk, Barnett T P, Bouwse, et al. Measurements of wind-wave growth and swell decay during the Joint North SeaWave Project (JONSWAP)[J]. Deutsche Hydrographische Zeitschrift, 1973, 8: 1-95.

[13] Madsen O S, Poon Y K, Graber H C. Spectral wave attenuation by bottom friction: Theory[J]. Coastal Engineering, 1988, 2: 492-504.

[14] Battjes J A, Janssen J P. Energy loss and set-up due to breaking of random waves[J]. Coastal Engineering, 2012, 1(16): 569-587.

[15] Kaminsky G M, Kraus N C. Evaluation of depth-limited wave breaking criteria[J]. Ocean Wave Measurements and Analysis, 1993, 2: 180-193.

[16] Mulligan R P, Bowen A J, Hay A E. Whitecapping and wave field evolution in a coastal bay[J]. Journal of Geophysical Research, 2008, 113(C03008): 1-16.

[17] 梁书秀, 孙昭晨, 尹洪强. 基于SWAN模式的南海台风浪推算的影响因素分析[J]. 海洋科学进展, 2015, 33(1): 19-29. Liang Shuxiu, Sun Zhaochen, Yin Hongqiang. Influence factors of typhoon wave forecast in the South Sea by SWAN Model[J]. Advances in Marine Science, 2015, 33(1): 19-29.

[18] 罗浩. SWAN模式渤海湾海浪数值模拟研究[D]. 天津: 天津大学, 2012. Luo Hao. Research on numberical simulation wave in bohai bay by SWAN model[D]. Tianjin: Tianjin University, 2012.

Numerical simulation of “CHAN-HOM” typhoon waves using SWAN model

YING Wang-min1, ZHENG Qiao1, ZHU Chen-chen1, ZHU Ye2, CHE Zhu-mei2, CHU Dong-dong1, ZHANG Ji-cai1
(1. Institute of Physical Oceanography, Ocean College, Zhejiang University, Zhoushan 316000, China; 2. The Ocean and Fisheries Bureau, Zhejiang Province, Hangzhou 310000, China)

Sep. 19, 2016

SWAN (simulating wave nearshore) model; CCMP (cross calibrated multi-platform); typhoon waves; the East China Sea; typhoon CHAN-HOM

In this study, a wave-simulation model is developed for the East China Sea based on the third-generation wave model simulating wave nearshore (SWAN). The model is forced by the cross calibrated multi-platform (CCMP), which is a wind data source with high temporal and spatial resolutions. In this paper, waves caused by 1509“CHAN-HOM” typhoon are studied and simulated. To determine parameterization for different effects and obtain accurate parameter values, several experiments are conducted to study factors affecting results of simulating typhoon waves, such as bottom friction, white capping, depth-induced wave breaking, and nonlinear wave-wave interactions. A number of reasonable recommendations are proposed after analysis of these factors. A comparison between model results and observation data obtained from four stations shows that simulated results meet the precision requirements of sea wave forecasting.

P733

A

1000-3096(2017)04-0108-10

10.11759/hykx20160919002

(本文编辑: 刘珊珊)

2016-09-19;

2016-11-16

国家重点研发计划(2017YFC1404000, 2017YFA0604100);浙江省自然科学基金项目(LY15D060001); 国家自然科学基金项目(41206001); 浙江省海洋与渔业局资助项目

[Foundation: the National Key Research and Development Plan, No.2017YFC1404000, 2017YFA0604100; the Natural Science Foundation of Zhejiang Province, No.LY15D060001; the Natural Science Foundation of China, No.41206001; The Foundation of Zhejiang Ocean and Fishery Bureau]作者简介: 应王敏(1995-), 男, 浙江台州人, 学士, 主要从事物理海洋、遥感方面研究, E-mail: qsy@zju.edu.cn; 车助镁, 通信作者, 高级工程师, 主要从事海洋预报工作, E-mail: tommyche@126.com