小题大做 变换思路 拓展思维——以一道中考模考“中档”题为例

□刘 莎

（宁波市海曙区鄞江镇中学，浙江宁波 315151）

小题大做 变换思路 拓展思维
——以一道中考模考“中档”题为例

□刘 莎

（宁波市海曙区鄞江镇中学，浙江宁波 315151）

对中考常见的关于反比例函数“中档”选择题进行小题大做，多视角审视，探究多种解决此类问题的思路，可以拓展学生的数学思维.

反比例函数；一题多解；变换思路

以平时学生常见的不起眼的小题着眼，变换多种解题思路，引领学生深入探讨，最后得出此类问题的若干处理方法，以到达培养学生分析问题、创新解决问题的目的.本文就以2016年中考模考中出现的一道关于反比例函数的“中档”选择题为例，呈现小题大做，变换解题思路，拓展学生思维.

一、原题呈现

例题（2016年浙江省宁波市中考模拟试题）如图1，在平面直角坐标系中，△ABC的顶点A，B分别在函数和的图象上，AB与y轴交于点C，且OC平分∠AOB，若，则k的值是（）

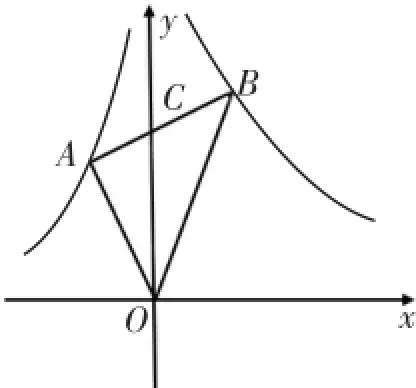
图1

这道选择题以反比例函数的概念和角平分线的性质为载体，不但可以考查学生的基础知识、基本技能和基本解题经验，而且还能够培养学生的思维品质和探究能力.

二、解法探究

思路1——着眼于选择题的试验筛选法

对于单项选择题，可以投“机”取“巧”，通过特殊情形的检验，就可以筛选出正确的答案，发挥由特殊鉴别一般的检测功能.

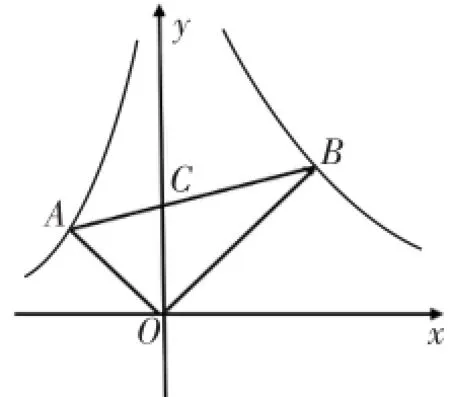
图2

解法1如图2，针对这道选择题，不妨在函数的图象上取点，由于 y轴平分∠AOB，则在函数的图象上可以把点B的坐标设为(m,m)，其中m＞0，则

则m=3，则k=m2=9，故可选（B）.

解法2不妨在函数的图象上取点，由于y轴平分∠AOB，则在函数的图象上可设A(-n,n)，其中n＞0，则解得n

则k=9，故可选（B）.

点评在解法1、解法2中，在两个函数的图象上所取的特殊点是它们与直线y=x或直线y=-x的交点，这使得运算最简单.

思路2——代入动点的参数坐标

假如这道题不是选择题，而是填空题或解答题的局部环节，那么就要探究一般性解法，这里考虑两个伴随动点 A和B的参数坐标.

解法3在函数的图象上任意取点，其中a＞0，由于y轴平分∠AOB，则在函数的图象上可以把点B的坐标设为，其中a，m＞0，则，则k=3m2.

则k=3m2=9，故选（B）.

……（以下类似于解法3）.

解法5根据，设 ||OA=r，，根据y轴平分∠AOB，设∠AOC=∠BOC=ϕ ，则 两 点 A(-rsinϕ,rcosϕ)、，代入函数式可得

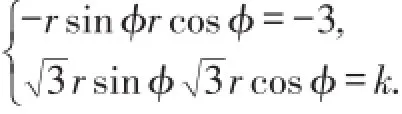
相除得k=9，故选（B）.

点评对动点进行审题的视角不同，就会牵引着不同思考侧重点，于是可以灵活引入不同的参数表示动点的纵横坐标，从而圆满解决问题.

思路3——利用面积和相似比

解法6如图3，作AF⊥y轴于F点，则作BG ⊥y轴于G点，同理得

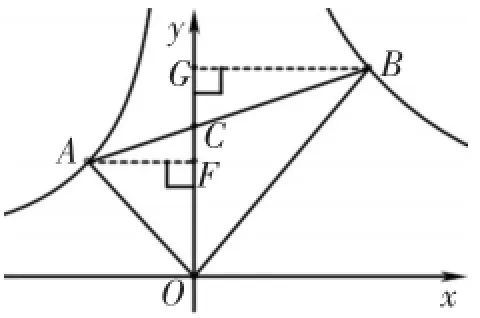
图3

由于∠AOF=∠BOG，

则Rt△AFO～Rt△BGO

所以k=3m2=9，故选（B）.

点评 琢磨解法6的相似比观点，启示着我们猜想并验证出新结论“任意两个反比例函数的图象必然相似或全等”.

思路4——利用轴对称图形

基于角平分线的题设条件，可以着眼于图形的对称性来寻找解法.

解法7如图4，考虑到y轴是∠AOB的角平分线，不妨沿着y轴将∠AOB折叠，就使函数图 象上的动点A正好对称翻折成OB上的点（记为 A′），则伴随动点 A′在函数图象上.

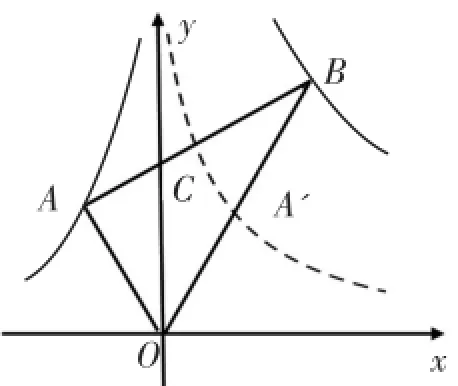
图4

设两点 A′，B在正比例函数 y=mx（m＞0）的图象上，分别通过解方程组得到

则m=9，故选（B）.

解法8提示：根据y轴是∠AOB的角平分线，可设直线OA，OB分别是正比例函数y=-mx，y=mx的图象……（以下类似于解法8）.

点评 解法7、解法8用两种不同方式构图，可以把题意的原始示意图转化成熟悉的几何基本图形，从而机智、从容地解决问题.

三、回顾升华

进一步思索上述问题的条件、结论和解题过程，还可以引导学生感悟到两个新结论——

结论1设k1∙k2＞0，若点A是过原点的直线l与反比例函数的图象的交点，点B是直线l与反比例函数的图象的交点，则

结论2设k1∙k2＜0，已知过原点的两直线l1，l2，点A是直线l1与反比例函数的图象的交点，点B是直线l2与反比例函数的图象的交点，若直线l1,l2关于y轴对称（或l1⊥l2），则

对于“中档”题的一题多解探究，有利于学生深刻理解数学的基本知识和基本思想，对于更为复杂的所谓难题，也会渐渐地有所提高.小处做“文章”，多角度、多视角拓宽学生的解题视野，从而提高学生的综合思维能力.