动点轨迹问题拓展性教学设计探究
□朱立斯
(湖州市第五中学,浙江湖州 313000)
动点轨迹问题拓展性教学设计探究
□朱立斯
(湖州市第五中学,浙江湖州 313000)
点的轨迹常以直线和圆弧为主.教师可以借助等长判别法和等角判别法两种方法帮助学生发现点的运动轨迹为圆弧,进而解决点的轨迹为圆弧的一类问题.也可以引导学生使用坐标判别法解决点的轨迹为直线的一类问题.
初中数学;动点轨迹;直线;圆弧
拓展性课程以培育学生的主体意识、完善学生的认知结构为宗旨,从教学内容、目标及过程中开发学生的潜能,促进学生个性的发展,是一种体现不同基础要求、具有一定开放性的课程.
近年来,在各地中考中出现一类求动点轨迹的问题,这一热点问题与高中数学教学紧密衔接,故以动点轨迹问题为专题的拓展性课程势在必行.由于较难确定动点轨迹的形状,学生往往无从下手.通过此课程的学习,能让学生领会解决动点轨迹问题的常用方法,提高学生综合运用圆与一次函数等知识的能力.在解决动点轨迹问题的过程中,渗透数形结合、函数、方程等思想方法,培养学生数学建模意识和将实际问题转化为数学问题的能力,发展学生的几何直观,鼓励学生发表自己的想法,勇于质疑,大胆创新,养成认真勤奋、独立思考、合作交流的学习习惯,形成严谨求实的科学态度.
一、点动成圆
(一)等长判别法
动点到某一定点的距离为定值.其原理为圆的定义:到一个定点的距离等于定长的点的轨迹.
例1如图1,一根长为2m的木棒AB斜靠在墙角处,此时BC为1m,当A点下滑至A处并且A′C=1m时,木棒AB的中点P运动的路径长为____.
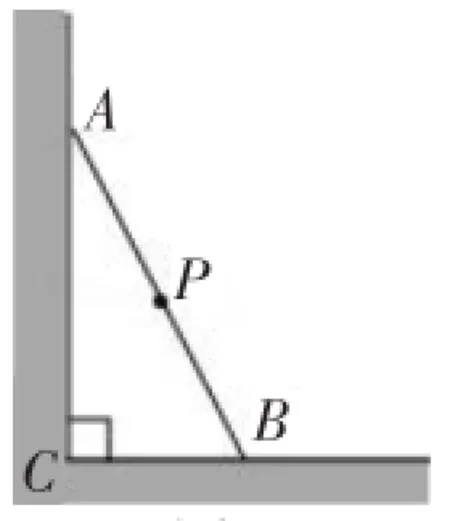
图1
答案解析如图2,连结CP,CP′.
∵∠ACB=90°,BC=1m,AB=2m,
∴∠BAC=30°,
∵P是木棒AB的中点,
∴PC=PA=1m,
∴∠PCA=30°,
同理求出∠B′CP′=30°,
则∠PCP′=30°,

图2
功能分析基础题.此题为学生之前遇到过的常规题,意在让学生回忆动点轨迹是圆弧
故答案为的情况,理解等长判别法的含义,理解动点到某一定点的距离为定值时,动点的轨迹是圆弧.
教学建议在学生自主解答的基础上,着重引导学生根据直角三角形斜边上的中线为斜边的一半这个性质得到动点P到定点C的距离为定值1,故动点P的运动轨迹为圆弧.
练习1如图3,在Rt△ABC纸片中,∠C=90°, AC=BC=4,点P在AC上运动,将纸片沿PB折叠,得到点C的对应点D(P在C点时,点C的对应点是本身),则折叠过程对应点D的路径长是____.
图3
答案解析∵∠C=90°,AC=BC,
∴△ABC是等腰直角三角形.
如图4,点D的路径是以点B为圆心,以BC的长为半径的扇形,路径长=

图4
故答案为:2π.
功能分析中档题.进一步理解动点到某一定点的距离为定值时,动点的轨迹是圆弧.培养学生挖掘隐含条件和潜在信息,理性分析运动过程中所保持的不变性质的能力.
教学建议在例1的基础上解决本题,许多学生有了经验方法,可以大胆放手让其尝试,教师只需适时点拨引导学生发现动点D到定点B的距离为定值4,故动点D的运动轨迹为圆弧.只需要知道动点D的起点与终点即可求出路径长.
变式1如图5,在平行四边形ABCD中,∠BCD=30°,BC=4,,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是_________.
图5
答案解析由题得动点A′到定点M的距离为定值2,故动点A′的运动轨迹为圆弧.作ME垂直CD的延长线于点E,由勾股定理易得:CM=7,故最小值为MC-A′C=7-2=5.
故答案为5.
功能分析拓展题.培养学生应用动点轨迹的知识解决其他类型的题目,拓宽学生的思维,增强学生对知识点的运用能力.
教学建议师生共同分析,教师可以让有能力的学生多发表自己的见解,抓住机会点拨,表扬他们,也可以鼓励其他学生积极探索,查找自己的思维误区,争取有新的突破.
(二)等角判别法
一动点与两定点所构成的角的度数为定值.其原理为圆周角定理:同弧或等弧所对的圆周角相等.反之,若一个动点P能使得以其为顶点的∠APB大小不变,且AB为固定线段,则点P就在以AB为一条弦且过点P的圆上运动(如图6).
图6
例2如图7,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为___________.
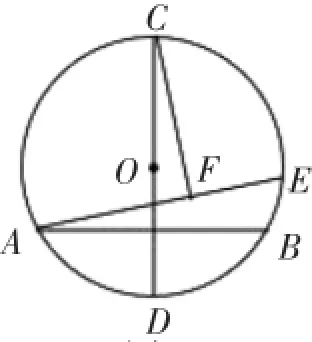
图7
答案解析如图8,联结AC,AO,由AB⊥CD,利用垂径定理得到G为AB的中点,由中点的定义确定出OG的长,在直角三角形AOG中,由AO与OG的长,利用勾股定理求出AG的长,进而确定出AB的长,由CO+GO求出CG的长,在直角三角形AGC中,利用勾股定理求出AC的长,由CF垂直于AE,得到三角形ACF始终为直角三角形,点F的运动轨迹为以AC为直径的半径,当E位于点B时,CG⊥AE,此时F与G重合;当E位于D时,CA⊥AE,此时F与A重合,可得出当点E从点B出发顺时针运动到点D时,点F所经过的路径长,在直角三角形ACG中,利用锐角三角函数定义求出∠ACG的度数,进而确定出所对圆心角的度数,再由AC的长求出半径,利用弧长公式即可求出的长,即可求出点F所经过的路径长为

图8
功能分析本题的解决,意在让学生理解当一动点与两定点所构成的角的度数为定值时,动点轨迹为圆弧.为后面的练习做铺垫.
教学建议师生共同分析,教师可以引导学生发现动点F与定点A,C所构成的角的度数为定值(即∠AFC=90°),故动点F的运动轨迹是圆弧,线段AC是直径,因此只要知道点F运动的起点与终点便可得出答案.
练习2如图9,直线y=-x+4与两坐标轴交于A,B两点,点P为线段OA上的动点,联结BP,过点A作AM垂直于直线BP,垂足为M,当点P从点O运动到点A时,则点M运动路径的长为____.
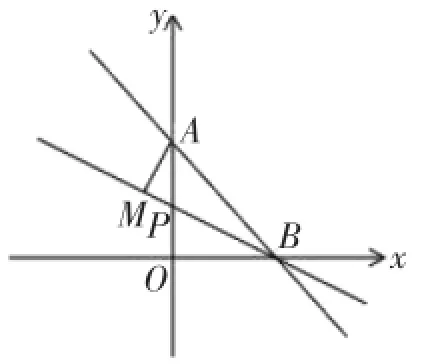
图9
答案解析根据直线与两坐标轴交点坐标的特点可得A,B两点坐标,由题意可得点M运动的路径是以AB的中点N为圆心,AB长的一半为半径的,易得的长度为
功能分析本题的解决,意在巩固学生对当一动点与两定点所构成的角的度数为定值时,动点轨迹为圆弧的理解.
教学建议 学生独立完成,师生共同订正答案.教师小结,等角判别法:动点与两定点所构成的角的度数为定值时,动点轨迹为圆弧.当动点M与定点A,B所构成的角的度数为定值(即∠AMB=90°),动点M的运动轨迹是圆弧,线段AB是直径.
变式2如图10,在边长为4的等边三角形ABC中,点D和点E分别是边AB和BC上的两个动点,且BD=CE,AE与CD相交于点P,则BP长度的最小值是____________.
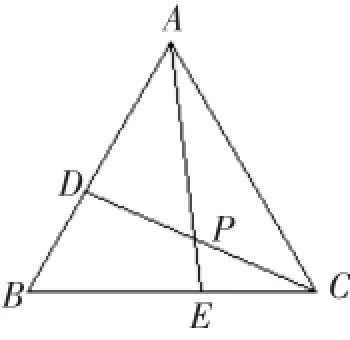
图10
答案解析由△BCD与△ACE全等可以得到动点P与定点A,C所构成的角的度数为定值∠APC=120°,故动点P的运动轨迹是圆弧,线段AC是弦.如图 11,易得 BP=
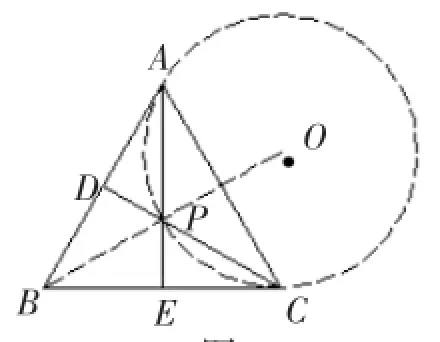
图11
功能分析拓展题.培养学生应用动点轨迹为圆弧的知识解决其他类型的题目,拓宽学生的思维,培养学生对知识点的运用能力.
教学建议师生共同分析,教师可以先引导学生发现图中△BCD与△ACE全等,再引导学生判别动点P的运动轨迹,最后让部分学生发表自己的见解,抓住机会点拨,表扬他们,也可以鼓励其他学生积极回答.
设计小结确定动点轨迹为圆的一般方法有两种,等长判别法和等角判别法.几何动点路径问题需要挖掘隐含条件和潜在信息,理性分析运动过程中所保持的不变性质,在此过程可通过画图(起点、终点、中间关键点)判断路径形状和范围,然后通过数学方法进行分析验证及几何建构进行转化.
二、点动成线
坐标判别法:当动点P的横纵坐标都能用同一个变量x(指数为1)表达时,则动点轨迹为一直线.
例1如图12,在平面直角坐标系中,A(2, 0),B(0,3),过点B作直线∥x轴,点P(a,3)是直线上的动点,以AP为边在AP右侧作等腰Rt△APQ,∠APQ= Rt∠,直线AQ交y轴于点C.当点P在直线上运动时,点Q也随之运动,则点Q运动路线的函数表达式为__________.
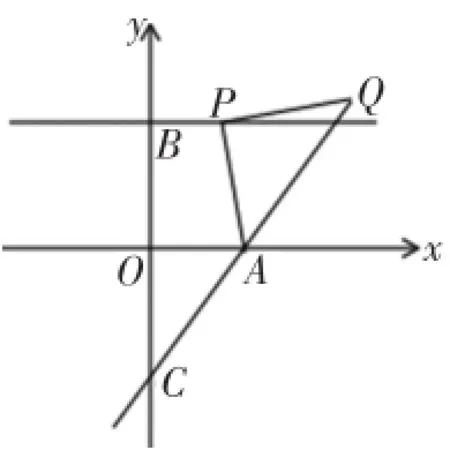
图12
答案解析过点P作EF⊥OA,垂足为E,过点Q作QF⊥EF,垂足为F,如图13.
易 得 △PEA≌△QFP.

图13
∴PE=QF,EA=PF.
若点P的坐标为(a,3),则PE=QF=3,EA= PF=|2-a|.
∴点Q的坐标为(a+3,5-a).
∵无论a为何值,点Q的坐标(a+3,5-a)都满足一次函数解析式y=-x+8,
∴点Q始终在直线y=-x+8上运动.
功能分析培养学生利用求出动点的坐标从而得知动点轨迹的判别方法.理解坐标判别法:当动点P的横纵坐标都能用同一个变量x(指数为1)表达时,则动点轨迹为一直线.
教学建议师生共同分析,教师可以先引导学生在直角坐标系中,根据条件求出点Q的坐标,再提示可以用K形图来解决这个问题,然后请学生回答解题步骤.最后再引导学生判别动点P的运动轨迹为一次函数即直线,最后师生一起解出最后答案.
例2如图14,已知AB=10,P是线段AB上的动点,分别以AP,PB为边在线段AB的同侧作等边△ACP和△PDB,联结CD,设CD的中点为G,当点P从点A运动到点B时,则点G移动路径的长是______.
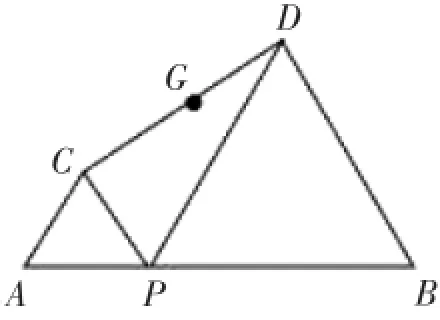
图14
答案解析建立直角坐标系使得A(0,0),B(10,0),P(x,0),
功能分析本题虽然不是在直角坐标系中,但也可以通过建立直角坐标系的方式解决这类动点问题,拓宽学生思维,培养学生的数形结合思想、创新能力等.
教学建议师生共同分析,教师可以先引导学生建立直角坐标系,设出动点P的坐标,从而引导学生解出点C和点D的坐标,最后解出点G的坐标,请学生逐一回答各个点的坐标,最后再引导学生判别动点P的运动轨迹为直线,只需要求出它的起点与终点,就能求出路径长.
练习 如图15,正方形ABCD的边长是2,M是AD的中点,点E从点A出发,沿AB运动到点B停止,联结EM并延长交射线CD于点F,过M作EF的垂线交射线BC于点G,联结EG,FG,P是MG的中点,则点P运动路线的长为__________.
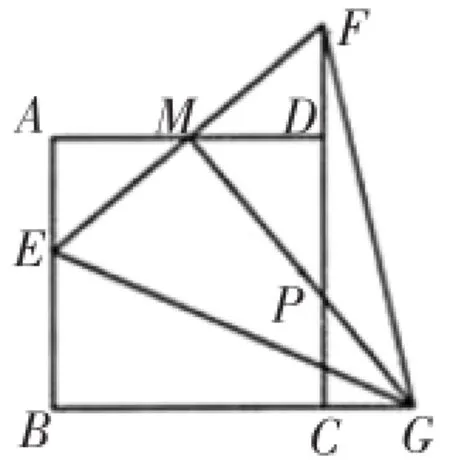
图15
答案解析建立直角坐标系使得A(0,2),B(0,0),C(2,0),D(2,2),M(1,2),E(0,x),则G的坐标可用含x的代数式表示,故动点P坐标也可用含x的代数式表示,则动点P的运动轨迹为一直线.易得F(2,4-x),由EG=FG可得G(-2x+3,0),P(-x+2,1),故点P运动路线的长为2.
功能分析加强学生利用建立直角坐标系解决动点轨迹问题的能力,拓宽学生思维,培养学生的数形结合思想、独立分析问题和解决问题的能力.
教学建议学生独立完成,师生共同订正答案.教师小结,当动点P的横纵坐标都能用同一个变量x(指数为1)表达时,则动点轨迹为一直线.只需要求出动点的起点与终点,就能求出路径长.
变式如图16,已知点A是第一象限内横坐标为的一个定点,AC⊥x轴于点M,交直线y=-x于点N.若点P是线段ON上的一个动点,∠APB=30°,BA⊥PA,则点P在线段ON上运动时,A点不变,B点随之运动.求当点P从点O运动到点N时,点B运动的路径长是_________.

图16
答案解析设,P(x,-x),则动点B的坐标可用含x和a的代数式表示,因为a是一个定值不是变量,所以动点B的运动轨迹为一直线.由∠APB=30°,BA⊥PA,得如图17,建立K形图,则△ABF∽△PAE,故,由PE=a+x,,得,故当x=0时,当时,,故路径长为

图17
功能分析拓展题.加深学生对点动成线问题的理解.
教学建议师生共同分析,教师可以先引导设出动点P与定点A的坐标,再引导学生利用K形图解出点B的坐标,最后再引导学生判别动点P的运动轨迹为直线,只需要求出它的起点与终点,就能求出路径长.教师可以让有能力的学生多发表自己的见解,抓住机会点拨,表扬他们,也可以鼓励其他学生积极发言,激发思维.
设计小结就初中数学而言,求动点路径长,不外乎求线段长或弧长.一般来说,在排除点动成圆的情况下,如果图形能建立合适的平面直角坐标系,借助函数知识,可以巧妙地解决这类点动成线的问题.这种数形结合思考问题的方法,是高中数学平面几何的基本方法.这种方法的学习为初高中知识的衔接,做了良好的铺垫.

