发展核心素养的数学教学设计构想
——以“多边形及其内角和”为例
□李 霞 徐铎厚(临沂光耀实验学校,山东临沂 276016;临沂青河实验学校,山东临沂 276016)
发展核心素养的数学教学设计构想
——以“多边形及其内角和”为例
□李 霞 徐铎厚
(临沂光耀实验学校,山东临沂 276016;临沂青河实验学校,山东临沂 276016)
从核心素养形成的角度出发,设计并实施“多边形及其内角和”一节的教学,需要让学生在思辨中形成概念,在化归中探寻策略,在类比中突破重点,在发散中丰富智慧,以此使学生学会用数学的眼光看世界,为终身发展而学习.
多边形内角和;教学设计;构想
“中国学生发展核心素养”所指向的“学生应具备的能够适应终身发展和社会发展需要的必备品格和关键能力”的意蕴和旨趣,彰显教师的教育智慧.数学核心素养要从教学行为与习惯的培养着手.
就拿“多边形及其内角和”来说,不论是概念的得出,还是公式的形成,都蕴含众多“关键能力”的形成要素.更进一步说,若教师舍弃“抓干的、来实的”的习惯做法,力透纸背,深入挖掘教材内容所承载的“关键能力”素材,将教学按照学生的认知逻辑展开,在“去粗取精、去伪存真、由表及里、由此及彼”的过程中,达成核心素养指向下的学生发展目标,课堂就会充溢智慧的霞光,绚丽而多姿.
一、在思辨中形成概念
本节课涉及众多相关概念,但“万物生长靠太阳”,再多的概念总有源头,这里的源头就是“多边形”,其关键点就是“多”.众所周知,“多”与“少”是相对的,此刻就需要教师指导学生认识“多”与“少”的辩证关系.多边形是新学内容,多到什么程度暂且不论,但“少”要少到什么程度呢?这就牵扯概念中的另一个关键字“边”.本节课是从“边”的多少出发研究图形,无边不成形,因此,从理论上讲,边(亦即线段)的数量最少是1,可以是2,学生也学过边数为3的三角形和边数为4的四边形.边数为1和2时,是开放式图形,属于“线段(直线、射线)”和“角”,三角形、四边形等才属于“多边形”意义下的“形”.从“少”出发,学生就会发现:多边形中的“边”,是线段;多边形是封闭图形;边数最少的多边形是三角形.
从“多”出发,学生就会发现,随着边数的增加,多边形中的一些元素也会发生一些变化:顶点增加;内角的个数增加;内角和会发生怎样的变化?有没有规律可循?(此时,学生的经验是三角形的内角和为180°,四边形的内角和为360°)由内及外,那外角和会发生怎样的变化?到此,又会牵扯出另一个问题:当多边形的边数无穷多时,多边形会发生什么样的变化?相关的要素又会发生怎样的变化?显然,这样的思考又是形成和发展极限思想的良好素材.
这样展开的教学,对学生发展来说因嵌入了学生的思考与发现,会比单纯按照学科逻辑(逐一交代概念)展开更使学生兴趣盎然.如果给予学生预习、讨论等“自由”的时间足够长,抑或是让每一个学生都把自己独立而独特的思考展示出来,说不定还能在凸多边形与凹多边形的比较中有更多的发现,求异思维的能力也会顺势得以培养.
有了这样的思考,学生理解教材中的多边形的概念及其相关内容——“在平面内,由一些线段首尾顺次相接组成的封闭图形叫作多边形.多边形按组成它的线段的条数分为三角形、四边形、五边形、六边形……由n条线段组成的多边形就叫作n边形”,就会更透彻.同样,多边形的角——内角、外角——连同内角和、外角和以及正多边形、多边形的对角线等,也不会存在理解的难度了.此处不再赘述.
二、在化归中探寻策略
从上述分析可以看出,三角形是边数最少的多边形,随着边数的增多,相关要素都会发生变化.从变化的观点出发,有两种可能:有规律的变化和无规律的变化.这就会生发“多边形的内角和与边的数量”之间存有什么样的关系的思考.对于这样的问题,学生可能会有无从下手的思维症结,就需要从思维的角度出发,找到突破的办法.从思维角度来讲,不论哪个学科,哪个领域,遇到复杂问题的时候,都会采用“复杂问题简单化”这一策略.在科学实验中经常运用的“控制变量法”,就是将复杂问题简单化处置的典型.面对“多边形”这一复杂问题,就要思考“最简单的多边形是什么图形”.前已述及,三角形就是最简单的多边形.这就找到了破解多边形相关问题的思维原点——三角形,这也是解决问题的出发点,由此引发学生去思考“如何将多边形变为三角形”的问题.
三、在类比中突破重点
从三角形出发考虑多边形问题,就要找到多边形转化为三角形的办法.其实,学生在这之前已经接触到解决这一问题办法,那就是求四边形内角和时所采用的“通过连接对角线将一个四边形变为两个三角形”,用这种类比的思想,不难发现,把四边形的对角线一连,就会出现两个三角形,那四边形的内角和就是两个三角形的内角和,即360°;对于五边形,可以通过连接对角线的方式,变为三个三角形,其内角和就是540°;以此类推,个数有限的多边形,其内角和的度数是可以计算出来的.从以上解决方式可以看出,“对角线”以及通过连接对角线而形成的“三角形”,就是解决多边形内角和问题的关键,对角线则是撬动多边形内角和问题的支点.
有了以上分析作铺垫,再让学生完成表1中的要求,学生自然兴趣盎然.
当学生完成这个表格后,多边形内角和的公式也就得到了:n边形的内角和等于(n-2)×180°.
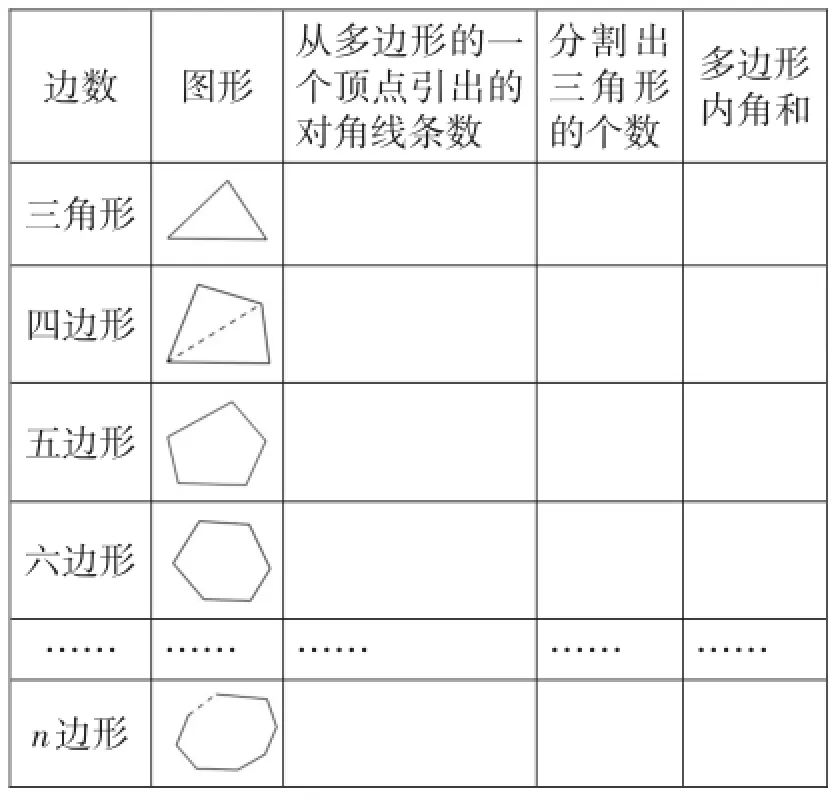
表1
四、在发散中丰富智慧
一个问题的解决,不会只有一个办法,否则,就不会有“条条大路通罗马”之说.唯有从多个角度探寻解决同一个问题的办法,学生的思维才能发散开来,并不断促使学生穷尽思维,进而理顺思维,优化思维,实现由解决一个问题向解决一类问题的突变,达到思维跃迁、智慧丰富之目的,生发不断创新的力量.
前述方法是从对角线出发,找到了一个解决多边形内角和的办法,再探寻其他办法,又应该如何思考呢?这还要回到几何图形的构成要素上寻找突破.
构成几何图形的基本要素,无非就是点、线、面.有的要素一目了然,比如,多边形中的边、顶点,有的要素则隐含在图形中,需要思考才能找到,比如刚才用过的对角线,类似的还有一些图形的高、角平分线、中线等等.上述解决问题的过程中,就是从多边形的一个顶点出发,在不相邻的另一个顶点间画出对角线,从而化归到三角形而找到了解决问题的支点.如此,同样从“点”这一思考原点出发,只是改变“点”的原始位置,比如,选择一条边的任意一个点构造出三角形,或者在多边形内(外)任意一个点构造三角形,都不失为可以采用的办法.这样,原来的“固定点”就会变为“移动点”“任意点”,而中考题中的重头戏,也往往如此选择.限于篇幅,简述如下:
方法二:在n边形的一边上任取一点,把这一点与各顶点联结,把n边形分割为(n-1)个三角形,这些三角形的内角和比n边形的内角和多出了一个平角,因此,n边形的内角和=(n-1)×180°-180,即为:(n-2)×180°.
方法三:在n边形内任取一点,然后把这一点与各顶点联结,将n边形分割为n个三角形,这n个三角形的内角和比n边形的内角和恰好多了一个周角360°,因此n边形的内角和=180°×n-360°,即为:(n-2)×180°.
方法四:在n边形外任取一点,然后把这一点与各顶点联结,将n边形分割为n个三角形,这n个三角形的内角和比n边形的内角和恰好多出了两个三角形内角和,因此n边形的内角和=n×180°-2×180°,即为:(n-2)×180°.
形成了这样的思维习惯,学生在今后的学习、工作、生活中,也会主动寻求“由静到动”“由此及彼”的途径,豁然开朗的就不仅是学习过程,会更多地表现在人生的幸福中.
从以上分析可以看出,本节内容涉及众多利于学生核心素养发展的要素,诸如对立统一、量变质变、有限与无限、个性与共性、一般与特殊、绝对与相对等,都极富哲学意味,若一一展开,必定是一幅幅美丽的风景.
从核心素养形成的角度来说,学生学习数学的一个重要目的是要学会数学的思考,用数学的眼光去看世界.这就需要教师在数学教学中应当从逻辑的、历史的、关系的等方面去展开,以“提出目标,创设情境,设计环节,穷极思维,形成技能,造就智慧”为终极追求,奠定学生终身发展的良好基础.
可见,充溢着思辨的学习,不仅有苟且,还有诗和远方!

