黑莓微波真空干燥传热特性

吴 涛 宋春芳 - 孟丽媛 -李臻峰 - 李 静 金光远 -

(1. 江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122；2. 江南大学机械工程学院，江苏 无锡 214122)

黑莓微波真空干燥传热特性

吴 涛1,2WUTao1,2宋春芳1,2SONGChun-fang1,2孟丽媛1,2MENGLi-yuan1,2李臻峰1,2LIZhen-feng1,2李 静1,2LIJing1,2金光远1,2JINGuang-yuan1,2

(1. 江苏省食品先进制造装备技术重点实验室，江苏 无锡 214122；2. 江南大学机械工程学院，江苏 无锡 214122)

对黑莓进行微波真空干燥，研究不同微波功率和真空度对黑莓干燥过程中温度的影响，观察样品整个温度场的分布规律。采用数值模拟的方法，建立电磁与传热耦合模型，经过2 min的微波真空加热，得出不同微波功率、不同真空度下黑莓的仿真温度场分布图。选取微波功率为400 W，真空度为-60 kPa的条件进行试验，对数值模拟的结果进行分析和评定。仿真的意义在于规避加热区域的冷点位置，同时选取合适的微波功率和真空度以降低热点区域的温度差异性，保证实际加热时同一批次的样品加热效果基本一致。结果表明：黑莓在微波功率为400 W，真空度为-80 kPa的条件下加热2 min后，热点的温度维持在60 ℃左右，温度差异性为0.27，在样品热点区域加热温度高度一致性的前提下，保证了合适的加热温度，满足黑莓的干燥要求。

黑莓；微波真空干燥；模拟仿真；温度场；优化；均匀性

黑莓为蔷薇科悬钩子属的浆果类果树，是第三代重要的小果类果树。黑莓于1986年引入中国，并于1994年开始推广，至2010年全国黑莓种植面积已达4 500 hm2以上，约占世界种植面积的1/5，已经成为亚洲最大的种植基地和世界知名产地[1]。黑莓营养丰富，口味独特，深受消费者青睐。由于其具有多种保健功效，所含有的花青素和VC能促进视网膜视紫质的再生而有效改善视力，因此受到医学界的广泛推崇[2]。黑莓鲜果柔软多汁，果实成熟期多在盛夏，常温贮藏仅为2～3 d，为易腐果品，不耐贮运，90%以上的鲜果加工成冻果，故对黑莓的深加工研究至关重要[3]。目前用于干制脱水的方法主要有真空冷冻干燥、热风干燥和微波干燥等[4]。真空冷冻干燥虽然得到的干制品质量好，但投资成本高；热风干燥存在干燥效率和能源利用率低等问题；微波干燥热效率高，但难以控制，易导致过热损害产品品质，出现烧焦、表面硬化等现象。微波真空干燥是在真空条件下利用微波能进行物料的干燥加工，它利用微波穿透力强，使物料内、外同时升温形成整体加热，缩短干燥时间，同时在真空环境下使水分能在较低温度下快速蒸发，防止物料氧化反应，较好地保留了黑莓的抗氧化成分。微波真空干燥在干燥品质方面优于热风干燥，接近冷冻干燥；在干燥效率方面优于冷冻干燥、单一微波干燥和真空干燥；具有干燥速率快，物料品质高和热利用率高等优点[5-7]。

随着计算机与计算机辅助工程的快速发展，高效的数值模拟使得计算机仿真成为理解复杂的微波真空加热过程的有效工具。建立仿真模型可以避免多次试验，同时避开试验条件的限制，缩短研究周期。目前国内外已有对微波加热温度场仿真模拟的研究报道，如Geedipalli等[8]通过模拟家用微波炉加热特性，运用有限元仿真计算带有旋转盘的微波炉瞬态加热过程；浦广益等[9]研究了食物位置对热风微波耦合加热效果的影响，用数值模拟的方法说明了微波加热存在温度不均匀性的问题，并用实验验证了模型的可行性。目前，涉及真空问题的数值模拟研究较为少见，黑莓微波真空加热的原理较为复杂，尚未见到相关的仿真模型。本试验用COMSOL软件对黑莓微波真空干燥过程进行仿真模拟[10]，观察黑莓瞬态传热特性，综合试验结果验证微波功率和真空度对黑莓干燥过程的温度影响规律，为工厂化果蔬干制技术的推广及其设备的改进提供理论依据，为产业化经营提供技术支持[11]。

1 微波真空加热物料的数学物理模型

微波加热物料过程的计算方法，目前较为成熟的是建立电磁与传热的耦合模型。其中，物料内部的电磁能量分布由麦克斯韦电磁场方程(Maxwell’s Equation)决定[12-14]：

(1)

式中：

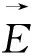
μr——相对磁导率；

εr——相对介电常数；

σ——电导率，S/m；

ε0——真空介电常数，F/m；

ω——电磁波的激励角频率，rad/s；

k0——自由空间波矢量，rad/m。

当电磁波穿过果蔬类的介电损耗介质时，其强度会减弱，部分电磁能被转换成物料内部的热能，电磁能转换成热能的耗散功率与损耗因子和电场强度的平方成正比[9]：

(2)

式中：

Pv——耗散功率，W/m3；

F——电磁波频率，Hz；

ε0——真空介电常数，F/m；

ε″——介电损耗因子。

耗散功率由傅里叶方程(Fourier Equation)决定：

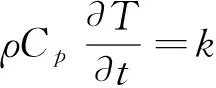
(3)

式中：

ρ——物料密度，kg/m3；

Cp——恒压比热容，J/(kg·℃) ；

T——仿真时间t时刻物料的温度，℃；

k——物料的热传导系数，W/(m·℃)。

加热物料的介电性能由介电常数和介电损耗因子来表征：

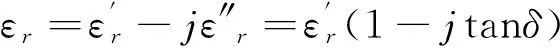
(4)

式中：

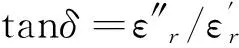
当加热物料的特性为各项同性的线性介质时，满足：

(5)

式中：

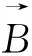
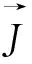
物料表面与周围的空气热交换可表示为：

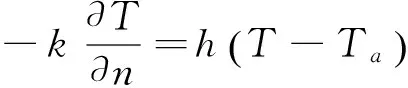
(6)

式中：

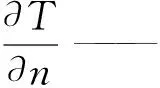
h——表面对流热传递系数，W/(m2·℃)；

Ta——初始温度，℃。

仿真过程中真空条件建立在空气密度上，微波真空装置的压强为p，相对真空度为p′(为负值)，标准大气压为patm，其中满足：

p=patm+p′。

(7)

空气密度应转换为与实时压强和温度相关的变量，将空气密度变量rho(PA[1/Pa]，T[1/K])[kg/m3]中的压强PA替换为式(7)中的p，同时将电磁频域模块和传热模块的压强由1.01×105Pa替换为微波真空装置的实际压强p。

2 材料与方法

2.1 试验材料

2.2 仪器设备

微波装置：江南大学机械工程学院自行组装；

循环水式多用真空泵：狮鼎SHB-B95型，郑州长城科工贸有限公司；

红外热成像仪：T440型，精度±2 ℃，美国FLIR Systems公司。

2.3 试验装置与几何模型

试验采用的微波真空装置见图1(a)，左侧为真空泵，装有显示真空度的仪表；右侧为微波干燥箱，内部腔体的尺寸为360 mm×360 mm×270 mm，波导位于腔体的顶部，以TE10模式进行传输，微波频率为2.45 GHz。建立几何模型见图1(b)，包括加热腔体、波导、塑料转盘、塑料盒以及均匀摆放的黑莓样品，其中转盘直径为320 mm，盛装黑莓的塑料盒尺寸为142 mm×112 mm×40 mm。建立黑莓模型时，对比真实黑莓，将黑莓建模为底面直径为18 mm，高为24 mm的圆柱体，共25个均匀排列在塑料盒中，总质量为160 g，见图1(c)。建立塑料盒模型时，考虑塑料盒的结构为一个长方体，设置长方体的4个侧面和底面为边界过渡条件，厚度为2 mm，内置材料为空气，边界材料为塑料，其效果等效为一个无盖，厚度为2 mm的塑料长方体容器盒。黑莓样品放置在塑料盒中，塑料盒放置在转盘的中心位置。模型具有较好的对称性，故在仿真时暂不考虑转盘的旋转，由于加热时间为120 s，时间较短，模型中不考虑黑莓样品中的水分变化。

图1 试验装置与几何模型Figure 1 Experimental setup and geometric model

2.4 网格划分

为了获得合理的数值模拟，模型的网格化分非常重要。Liu等[17]提出在保证运算时间最快及良好的温度仿真结果的情况下，在2.45 GHz频率时划分物料最合适的网格尺寸与自由空间波长(λ=12.24 cm)和介电常数存在如下关系：

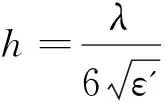
(8)

由此可知，在划分网格时，黑莓的最合适网格尺寸为2.55 mm。启用物理场控制网格， 最大网格单元尺寸控制参数采用最大频率f0，这样既能保证运算时间较短，同时计算结果相对精确[18]。网格划分结果见图2。

图2 微波真空装置和黑莓的网格划分Figure 2 Meshing scheme of the microwave vacuum device and blackberry

2.5 仿真方法

仿真过程设置6种条件见表1，干燥时间设置为2 min，模型中瞬态研究设置为range(0，1，120)，时间单位为s。由于微波加热具有不均匀性，为了研究方便，选取黑莓样品模型的最高温度点作为研究对象，由于模型的高度对称性和微波加热的特点，点的选取是合理的，保证了变量的单一性(即认为温度最高点始终在某一个确定位置)。在模型中找出每种试验条件下选取点达到稳定温度所需要的时间和最终的稳定温度，作为后续分析使用。在模型中选取其他6个相对热点的位置点进行微波真空干燥的温度差异性分析。模拟仿真流程见图3。

表1 试验条件Table 1 Experimental conditions

2.6 温度测量

将制备好的黑莓样品放入微波真空装置中加热，加热时需注意先将微波装置里的压强抽至对应的真空度，然后开启微波加热按钮。加热至对应时间后，快速取出样品并放入提前预热的保温箱中保温，使用红外热成像仪记录黑莓表面的空间温度场分布图[19-20]，然后用图像分析软件FILR拾取温度场分布图上选取点的温度，每组试验重复测量3次，作为试验最后结果。仿真中黑莓对应点的瞬态温度可由COMSOL软件中的点计算得到。

图3 模拟仿真流程Figure 3 Simulation process

3 结果与讨论

3.1 仿真结果分析

3.1.1 相同功率不同真空度条件下黑莓样品的温度分布图

图4(a)、(b)、(c)、(d)分别对应于试验序号为1、2、3、6试验条件(即微波功率为400 W，真空度分别为-40，-80，-60，0 kPa)下黑莓样品2 min加热后的温度分布图。由图4可以观察到黑莓样品的整体温度分布规律，对应于真空度0，-40，-60，-80 kPa下最高温度值依次为97.2，87.2，75.1，68.2 ℃，其原因在于随着真空度绝对值的增加，水分能在较低温度下蒸发，保证物料在低温条件下进行干燥。

3.1.2 相同真空度不同功率条件下黑莓样品的温度分布图

图5(a)、(b)、(c)分别对应于试验序号4、3、5试验条件(即真空度为-60 kPa，微波功率分别为300，400，450 W)下接近稳定温度时刻的黑莓样品温度分布图，功率从300 W增大到400 W时，时间由55 s降到39 s；功率由400 W增大到450 W时，时间由39 s降到31 s。随着微波功率的增加，样品最高温度点趋于稳定温度时所耗时间逐渐减少。

3.1.3 不同仿真条件下的结果参数表 综合图4、5和表2可知，微波功率影响黑莓的温度上升速率，真空度影响黑莓加热2 min后的最终稳定温度。从试验序号4、3、5得出的仿真结果可以看出，相同真空度的条件下，随着微波功率增加，接近稳定温度所需时间越短；-60 kPa的真空度条件下，微波功率300，400，450 W对应的接近稳定温度所需时间依次为55，39，31 s。从试验序号6、1、3、2得出的仿真结果可以看出，相同微波功率的条件下，随着真空度绝对值增大，最终稳定温度越来越低，400 W的微波功率条件下，真空度0，-40，-60，-80 kPa对应的黑莓样品热点最终稳定温度依次为97.2，87.2，75.1，68.2 ℃。同时，从试验序号4、3、5还可以看出，相同真空度的情况下，随着微波功率增加，黑莓样品最终稳定温度有所增加，但影响不大；-60 kPa的真空度条件下，微波功率300，400，450 W对应的黑莓样品热点最终稳定温度依次为74.1，75.1，75.4 ℃。

Figure 4 The temperature distribution of Blackberry samples under the different vacuum degrees and same power conditions after drying 2 min

图5 相同真空度不同功率条件下黑莓样品 接近稳定温度时刻温度分布图

Figure 5 Temperature distribution near the stable temperature of Blackberry samples under the different powers and same vacuum degree conditions

表2 不同仿真条件下的结果参数表Table 2 Results parameters under different simulation conditions

3.1.4 不同条件下黑莓样品温度分布的差异性 仿真完毕后，观察黑莓样品的温度分布规律，选取黑莓样品区域上温度相对较高的位置点c1、c2、c3、c4、c5、c6，见图6。在COMSOL软件中计算出这6个位置点微波真空加热2 min后温度，求出每种仿真条件下这6个位置点的温度标准差，用来反映不同位置点的温度差异性，见表4。其中标准差的计算公式为：

图6 相对热点的6个位置点Figure 6 The 6 points of the relative hot spots表3 不同仿真条件下不同位置的温度标准差

Table 3 Standard deviation of temperature at different positions under different simulation conditions

试验序号c1c2c3c4c5c6标准差σ179.9482.9082.9183.8183.3082.701.24259.0159.3959.4359.7859.7659.230.27372.2673.5273.5273.8773.8373.870.57461.1873.2573.2273.3973.4871.194.36572.8273.6173.4174.4273.7873.320.48679.6892.7392.8093.9893.1692.665.01

(9)

式中：

σ——6个位置点的温度标准差；

xi——第i个位置点的温度，℃；

μ——6个位置点的平均温度，℃。

从试验序号4、3、5得出的仿真结果可以看出，相同真空度的条件下，随着微波功率增加，热点的温度差异性越来越小；-60 kPa的真空度条件下，微波功率300，400，450 W对应的温度标准差依次4.36，0.57，0.48。从试验序号6、1、3、2得出的仿真结果可以看出，相同微波功率的条件下，随着真空度绝对值增大，热点的温度差异性越来越小；400 W的微波功率条件下，真空度0，-40，-60，-80 kPa对应的温度标准差依次为5.01，1.24，0.57，0.27。真空度由-60 kPa到-80 kPa时，标准差变化不大。由此可知，在追求加热效果一致的同时，也要根据实际的试验装置和试验条件来合理安排微波功率和真空度，在加热过程中也可根据试验情况作合理调整[21]。

3.2 模型验证

3.2.1 空间温度分布 选取微波功率为400 W，真空度为-60 kPa的条件，对黑莓进行2 min的干燥试验。试验前准备36组黑莓样品，为确保加热的连续性，对不同组样品加热10，20，30……120 s后分别取出，取出后的样品不再进行后续加热。待样品干燥至对应时间后，快速取出并放入提前预热的保温箱中保温，使用红外热成像仪记录黑莓样品表面的空间温度场分布图。试验时应确保预热保温箱的温度与加热后取出的样品温度基本相等，避免由温差引起测量误差。每组试验重复3次，作为试验最终结果。验证时，在样品上取5个点，对应于仿真模型的p1、p2、p3、p4、p5点，见图7(a)。用红外热像仪图像分析软件FILR拾取温度场分布图上对应点的温度，作为后续处理试验数据使用。最后得出不同位置仿真与试验的温度对比图，用来验证仿真模型。

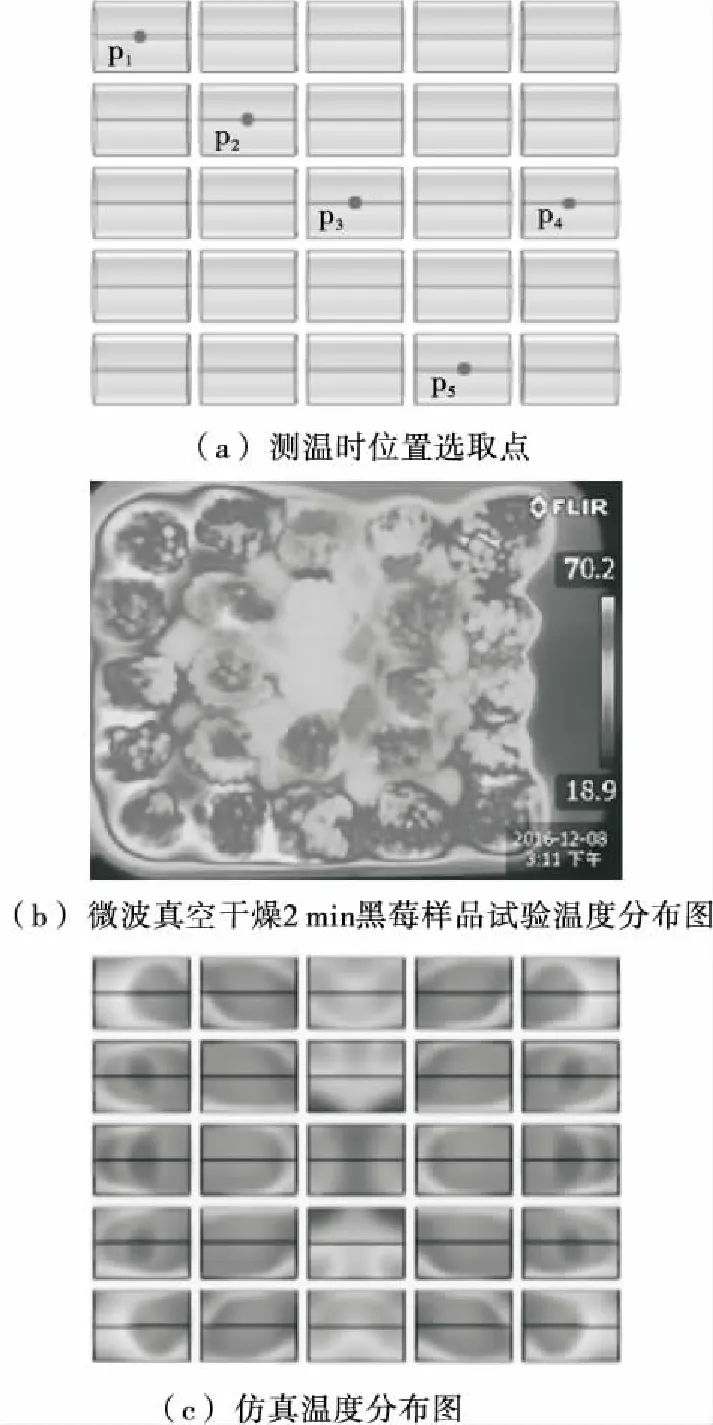
图7 位置点选取图和加热2 min后试验与仿真的 空间温度分布图

Figure 7 Location selection graph and the spatial temperat-ure distribution of experiment and simulation after heating 2 min

微波功率为400 W，真空度为-60 kPa时，微波加热2 min后试验与仿真的黑莓空间温度场分布见图7(b)和(c)。仿真与试验均显示中心黑莓样品的温度低于边缘黑莓样品的。总体而言，仿真的空间温度场分布与试验结果保持一致。

3.2.2 瞬时温度曲线 仿真与3次重复试验所得的瞬态温度随时间的变化见图8。由图8可知，黑莓在微波真空加热的过程中，温度先是呈线性趋势上升，随后缓慢上升逐渐趋于稳定。在p1、p2、p4、p5相对热点位置，仿真的温度略高于试验温度，p3冷点位置实际温度略高于仿真温度，这主要是因为仿真模型较为理想，总体上试验和仿真结果较为吻合。

图8 不同位置的温度在仿真与3次重复试验 中随时间的变化

Figure 8 Time-dependent temperature at different locations in the simulation and the 3 replicates experiment

4 结论

(1) 仿真空间温度场分布与瞬态温度曲线与试验结果保持一致，模型是可行的。该模型可用于分析微波真空干燥过程中样品的温度变化，避免了试验过程中测温破坏真空环境，导致加热的不连续性。模型可以很好地预测微波真空加热的冷点位置，选择相对热点位置以保证加热的高效性。

(2) 仿真结果表明，随着微波功率的增加，相对热点的温度差异性降低，功率由300 W增加到400 W时，标准差由4.36降到0.57，降幅明显；功率由400 W增加到450 W时，标准差由0.57降到0.48，降幅较小。但是随着微波功率的增大，会加快模型热点位置温度上升速率，在实际干燥过程中，热点长时间处于高温位置，材料属性会发生较快变化，容易出现烧焦、糊化等现象；随着真空度的增加，相对热点的温度差异性也降低，真空度由-40 kPa增加到-60 kPa时，标准差由1.24降到0.57，降幅明显；真空度由-60 kPa增加到-80 kPa时，标准差由0.57降到0.27，降幅较小。但是随着真空度绝对值的增加，会影响样品的干燥温度，降低干燥速率，并且对试验设备要求较高。综上，实际干燥过程中应综合考虑，合理选取微波功率和真空度。

(3) 模型考虑的是整个加热腔体的真空环境，并未考虑黑莓材料内部真空环境的影响，这是模型的不足之处。模型为后期研究干燥失水率和干燥后营养物质的保留提供了理论支持。

[1] 李维林, 吴文龙, 张春红, 等. 世界黑莓产业发展和研究现状及前景[J]. 植物资源与环境学报, 2012, 21(3): 105-115.

[2] 李维林, 孙醉君, 郑海燕. 黑莓鲜果及其加工品的营养成分[J]. 天然产物研究与研发, 1998(14): 55-59.

[3] 吴文龙, 王小敏, 赵慧芳, 等. 黑莓品种“Chester”鲜品贮藏性能的研究[J]. 食品科学, 2010, 31(8): 280-284.

[4] 王顺民, 谭玉霞, 韩永斌, 等. 热风与微波及其联合干燥对菠菜干制效果的影响[J]. 食品科学, 2012, 33(20): 80-84.

[5] 吕丽爽. 微波干燥技术在食品中的应用[J]. 食品与机械, 2006, 22(5): 119-122.

[6] 朱德泉, 王继先, 钱良存, 等. 猕猴桃切片微波真空干燥工艺参数的优化[J]. 农业工程学报, 2009, 25(3): 248-251.

[7] 李波, 芦菲, 刘本国, 等. 双孢菇片微波真空干燥特性及工艺优化[J].农业工程学报, 2010, 26(6): 380-384.

[8] GEEDIPALLI S S R, RAKESH V, DATTAA K. Modeling the heating uniformity contributed by a rotating turntable in microwave ovens[J]. Food Eng., 2007, 82(3): 359-368.

[9] 浦广益, 宋春芳, 续艳峰, 等. 食品位置对热风微波耦合加热效果的影响[J]. 食品与生物技术学报, 2015, 34(6): 593-597.

[10] William B J Zimmerman, 中仿科技公司. COMSOL Multiphysics有限元法多物理场建模与分析[M]. 北京: 人民交通出版社, 2007: 143-158.

[11] 常虹, 李远志, 龚丽. 微波真空干燥菠萝粉初步研究[J]. 食品与机械, 2008, 24(3): 112-115.

[12] SEKKAK A, PICHON L, RAZEKA. 3-D FEM Magneto-thermal analysis in microwave ovens[J]. IEEE Trans Magnetics, 1994, 30(5): 3 347-3 350.

[13] FRANCOIS Torres, BEMARD Jecko. Complete FDTD analysis of microwave heating processes in frequency-dependent and temperature-dependent media[J].IEEE Trans on Microwave Theory and Techniques, 1997, 45(1): 108-116.

[14] VARITH J, DIJKANARUKKUL P, ACHARIYAVIRIYA A, et al. Combined microwave-hot air drying of peeled longan [J]. Journal of Food Engineering, 2007, 81(2): 459-468.

[15] Online Computer library Center, Inc. COMSOL Multiphysics 简介[EB/OL]. [2017-02-15]. http://cdn.comsol.com/documentation/5.2.1.262/IntroductionToCOMSOLMultiphysics.zh_CN.pdf.

[16] 桑田, 宋春芳, 袁冬明, 等. 基于微波干燥的黑莓介电特性研究[J]. 浙江农业学报, 2016, 28(2): 345-351.

[17] LIU Shi-xiong, FUKUOKA M, SAKAI N. A finite element model for simulating temperature distributions in rotating food during microwave heating [J]. Journal of Food Engineering, 2013, 115(1): 49-62.

[18] Online Computer library Center, Inc. Microwave oven [EB/OL]. [2017-02-15]. http://www.cn.comsol.com/model/microwave-oven-1424.

[19] SONG Chun-fang, WANG Yan, WANG Shu-guang, et al. Non-uniformity investigation in a combined thermal and microwave drying of silica gel[J]. Applied Thermal Engineering, 2016, 98: 872-879.

[20] PITCHAI K, CHEN J, BIRLA S, et al. A microwave heat transfer model for a rotating multi-component meal in a domestic oven: Development and validation[J]. Journal of Food Engineering, 2014, 128: 60-71.

[21] 张丽晶, 林向阳, ROGER Ruan, 等. 绿茶微波真空干燥工艺的优化[J]. 食品与机械, 2010, 26(2): 143-146.

Analysis of heat transfer characteristics of Blackberry microwave vacuum drying

(1.JiangsuKeyLaboratoryofAdvancedFoodManufacturingEquipmentandTechnology,Wuxi,Jiangsu214122,China; 2.SchoolofMechanicalEngineering,JiangnanUniversity,Wuxi,Jiangsu214122,China)

Microwave vacuum drying of blackberry was carried out to investigate the effect of microwave power and vacuum degree on the temperature of blackberry during drying process, and the distribution law of the whole temperature field was observed. Using numerical simulation method, the coupling model of electromagnetic and heat transfer was established. After two minutes of microwave vacuum heating, the simulation temperature field distributions of blackberry under different microwave power and vacuum degree conditions were obtained. The experiment was carried out under the condition of microwave power of 400 W and vacuum degree of -60 kPa, and the experiment and simulation results were compared to analyze and evaluate the results of numerical simulation. Simulation can observe and avoid the hot and cold spots. The appropriate microwave power and vacuum were also selected by simulation to reduce the temperature difference and ensure heating uniformity. The results showed that blackberry under the condition of the microwave power of 400 W and vacuum degree of -80 kPa after heating 2 min, the temperature of the hot spot was maintained at about 60 ℃, with the temperature difference about 0.27. The heating uniformity was consequently ensured to meet the drying requirements of the blackberry.

Blackberry; microwave vacuum drying; simulation; temperature field; optimization; uniformity

10.13652/j.issn.1003-5788.2017.04.011