基于用户聚类的社交网络影响力最大化传播模型

曾燕清，陈志德，李翔宇

(1. 福建江夏学院，福建 福州 350108；2. 福建师范大学，福建 福州 350007) 3. 闽江师范高等专科学校，福建 福州 350007)

基于用户聚类的社交网络影响力最大化传播模型

曾燕清1，陈志德2，李翔宇3

(1. 福建江夏学院，福建 福州 350108；2. 福建师范大学，福建 福州 350007) 3. 闽江师范高等专科学校，福建 福州 350007)

本文针对的是社交网络中的影响力最大化问题。在经典线性阈值传播模型基础上，对社交网络中的用户进行聚类分析，并在此基础上提出改善的K-LT传播模型。在K-LT传播模型基础上，进一步提出K-KK影响力最大化算法。通过采集真实社交网络数据，进行试验仿真。试验结果表明，改进的K-KK影响力最大化算法与未改进时相比，算法性能有较好提升。

社交网络；传播模型；影响力最大化

0 引言

社交网络影响力是指用户受其他社交网络用户信息传播的过程。社交网络中影响力最大化问题是指在给定传播模型的情况下，从网络中选取k个初始种子节点，让其在网络中传播影响，使得最终传播影响范围最大。信息在社交网络传播过程中都遵循一定的规则，这些规则称为传播模型。挖掘社交网络中有影响力的用户，在营销、信息检索、信息推荐和社区挖掘[12-14]等领域都得到了广泛的应用。因而，在给定播模型基础上，研究影响力最大化问题具有重要应用价值。传播模型主要可以分为基于传播过程的模型、基于影响力的模型和基于转发因素的模型。主要的一些基本传播模型有线性阈值模型（LTM）、独立级联模型（ICM）、加权级联模型（WC）和热传播模型等[1]。在经典的线性阈值模型中，对节点的差异性处理是通过节点的出入度，即节点的网络结构来体现的，节点的权重和阈值则属于随机生成，无法体现不同个体对信息的要求高低，也无法体现对其他个体影响的差异。我们认为网络中除出入度以外，节点的相关性和重要性是衡量其影响力重要指标。因此，本文基于两种考虑：不同用户对信息需求不同、不同用户影响力不同，提出基于用户聚类的改进的K-LT传播模型，并在该传播模型下对KK贪心算法进行改进，提出基于用户聚类的K-KK贪心算法来近似求解影响力最大化问题。实验表明，在本文提出的传播模型中，其传播过程相较于传统线性阈值传播模型更接近于实际传播过程；在该模型下处理影响力最大化问题相较于传统线性阈值传播模型而言，计算效率大幅度提高，并且传播效果并未消耗传播效果。

本文第二节介绍相关工作；第三节对问题进行定义；第四节介绍本文提出的K-LT模型和寻找Top-k节点的贪心算法K-KK；第五节中我们将介绍在采集的数据集上进行的实验及结果分析；在本文最后将对工作进行总结。

1 相关工作

影响力最大化问题是社交网络研究中的重要问题，该问题最早由Domingos和Richhardson等人[2]提出。在此基础上，Kempe等[3]提出top-k影响力最大化问题，即如何在网络中找到k个初始节点使得通过这k个节点所产生的影响传播范围最大。同时，Kempe等人证明，在线性阈值和独立级联模型下，影响力最大化问题为NP难问题[4]，并提出了近似比为（1-1/e）的KK贪心算法来解决此问题。该贪心算法的复杂度太高，对大规模社交网络而言伸缩性将遇到挑战。为解决贪心算法效率问题，研究者们提出了一系列改进的贪心算法和新的启发式算法。

Leskovec等[5]通过改进影响函数的子模特性，提出CELF算法，此算法很大程度上减少了评估种子影响范围的次数，但当网络规模迅速扩大时，仍有计算量大问题。Goyal等在CELF基础上提出了CELF++算法，进一步提高了算法性能[6]。Chen[7]等人对Kempe的贪心算法进行了优化，随后提出degree-discount算法，改算法提升了计算性能，但其基于在独立级联模型下所有边影响概率值相同的假设，跟实际传播过程不符。除了贪心算法之外，还有启发式算法。Chen和Wang在LT传播模型下，提出构造局部有向无环图的启发式算法LDAG[8]，但改算法只考虑相邻节点的直接影响力。Kimura和Saito等提出了基于最短路径的SPM和SP1M模型[9],在SPM和SP1M模型下，节点的影响力范围可以进行准确计算，但这些模型未考虑用户的影响力问题，仅仅使用最短路径而忽略影响力在传播过程中的重要作用。在以上介绍的模型中针对LT模型提出的方法在衡量节点差异性时，是通过节点的出入度来体现；而节点的权重和阈值则基于随机生成的假设，未考虑不同类型个体对信息的要求高低和对其他个体影响力的差异。基于以上考虑，本文研究考虑个体信息要求差异和影响力差异的社交网络影响力最大化问题，首先对用户进行聚类分析，以优化阈值和影响力参数；接着提出基于聚类的改进的K-LT传播模型；再给出基于聚类的优化的K-KK贪心算法，并通过实验对比了所提出的算法的性能。

2 问题定义

2.1 传播模型

给定社交网络图G=(V, E, w)，其中V表示网络中的节点集合，E表示节点间边的集合，w表示边上的权重，则传统线性阈值传播模型是以接受者为中心的模型。则给定活跃节点初始集合A，信息传播模型M可以表示如下表1所示：

表1 线性阈值传播模型Tab.1 Linear-threshold propagation model

其中，阈值θv表示当父节点u为活跃节点（该节点发表或转发了某个信息）时，其子节点v成为活跃节点的潜在倾向性概率。LT模型是一个与0-1分布有关的概率模型，节点的阈值θv在[0,1]范围内选取随机值；ω(u，v)表示v节点的活跃父节点对v的影响权重，同样是随机生成，且∑ω(u，v)≤1。基于以上描述，对于一个给定的活跃节点初始集合A（A∈V），用RS(A)表示社交网络中最终活跃节点的集合，φ(A)＝|RS(A)|表示随机激活过程结束时活跃节点的个数，φ(A)是一个随机变量，用δ(A)表示φ(A)的期望值，我们称δ(A)为初始集合A的影响度。

在上述线性阈值模型中，节点的差异性是通过节点的出入度，即节点的网络结构来体现的。而所有节点的权重和阈值都用同样的随机方式生成，且生成值时取值区间相同，无法体现不同个体对信息的要求高低，以及不同个体对其他个体影响力的差异。为了更好的模拟现实中的社交网络，我们将在下一节中使用聚类方法来优化阈值和影响力参数。

2.2 影响力最大化问题定义

在给定上述线性阈值传播模型下，我们可以对影响力最大化问题进行定义。

定义1 给定社交网络G=（V,E,w）、传播模型M和k≤|V|，寻找k个节点的种子集合，使得φ(A)=|RS(A)|最大，RS(A)表示社交网络中最终活跃节点的集合，φ(A)表示在传播模型M下传播结束后激活的节点的总数目。

3 K-LT及K-KK算法

3.1 用户聚类分析

在社交网络中，依照用户在社交网络上的转发数、出入度和发帖频率等属性，可以将用户分为核心用户、活跃用户、非活跃用户和水军等不同类别。对于不同类别的用户，其在LT模型中的阈值θ和影响权重ω都会有显著差异，应差别处理。故本节中将对用户进行聚类分析。

k-means是经典的聚类划分算法之一，它把集合D中的对象划分为k个簇，并通过目标函数评估簇的质量，使簇内对象相似，簇间对象相异。它的基本算法原理如下表2所示：

表2 k-means算法基本原理Tab.2 K-means algorithm

使用k-means算法进行聚类的第一步，需要确定k的数量。在对社交网络用户进行分析的模型中，我们将k定义为用户可以划分的类型数目。根据社交网络的用户特征，可以将用户分为六种类型[12]:游民型用户、关注他人型用户、积极型用户、自我关注型用户、持久贡献型和明星型用户。按照其受影响阈值和影响力的差异，可以将上述类别进一步合并为三类：核心用户、活跃用户和非活跃用户。对应到聚类的结果中，可以参照各个簇的数据特征将其定义：被转发较多的核心用户、转发较多而被转发较少的活跃用户、转发和被转发都较低的非活跃用户，故本文中将k的值定义为3，对用户进行聚类分析，聚类结果将在实验部分给出并进行分析。聚类分析结束后，将聚类的结果作为本文所提出改进的K-LT线性阈值模型的输入，具体将在下一节中阐述。

3.2 K-LT线性阈值模型

在确定用户的聚类数目后，对三类用户的阈值选择区间参数进行优化：考虑核心用户是被转发较多，设定核心用户V1:[a,1];活跃用户是转发较多而被转发较少，设定V2：[0,1];非活跃用户转发和被转发都较少，设定V3:[b,1]。对于影响力同样加入权重：核心用户对其他用户影响较大，设定核心用户V1：从c*ω(u，v)；活跃用户V2:ω(u，v);非活跃用户V3：d*ω(u，v)。参照微博中三类用户的转发量比例[10]，本模型中，设定参数取值为：a=0.5，b=0.2，c=2，d=1/2。给定活跃节点的初始集合A，则信息按照如下表3中所示过程进行传播。

以上得到基于聚类优化的线性阈值K-LT模型，模型模拟了社交网络的信息传播过程，以该信息传播模型为基础，将在下一节中进一步解决影响力最大化问题。

3.3 K-KK影响力最大化贪心算法

KK贪心算法的影响最大化效果较好，最优解概率大于60%，但缺点在于计算量较大。算法的每一步都要重新计算未激活节点的边际效应，时间复杂性为O（n^2*m*n），m为每个节点的平均边数，n为图中所有节点的总数。由于核心用户节点的影响力远高于其他节点，故可进行假设最大影响力的节点一定在核心用户中。基于上述假设，在加入聚类优化后，可以将节点选择的范围从全部未激活节点集合，缩小至未激活的核心用户节点集合；进而可以大幅减少计算量以优化这一问题。基于以上考虑，我们对KK算法进行改进，提出基于聚类的优化的K-KK算法，改进后的算法如下表4所示。

表3 K-LT传播算法Tab.3 K-LT propagation model

通过聚类优化后，K-KK算法选择节点的范围从过去的KK算法全部节点V范围，缩小到了核心节点集V1范围，大幅减少了计算量、提高算法效率。

表4 K-KK算法Tab.4 K-KK algorithm

4 实验分析

4.1 实验数据获取及预处理

我们用具有开放性、交流内容公开和用户关系公开等特性的微博平台作为实验对象，获取真实网络数据集对算法性能进行验证。数据集是通过编写网络爬虫在新浪微博上以某个节点为初始节点，按广度优先方式，进行数据爬取，爬取流程如图1所示。

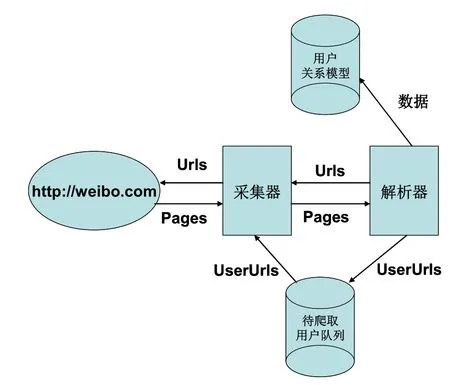
图1 微博用户关系爬取流程Fig.1 Micro-blog user relationship crawling process

爬虫先模拟登陆新浪微博，从种子节点用户ID开始，首先采集该节点节基本信息，并用解析器进行数据解析，然后获取该节点的关注列表和粉丝列表网页URL，接着通过关注列表和粉丝列表网页URL获取关注或粉丝用户ID和URL信息，并放入待爬取队列，以此类推，直到达到指定的的爬取深度N为止。但是，新浪微博具有反爬策略，每个用户最多只能采集其200个关注用户和粉丝用户，用户基本信息如表5所示。

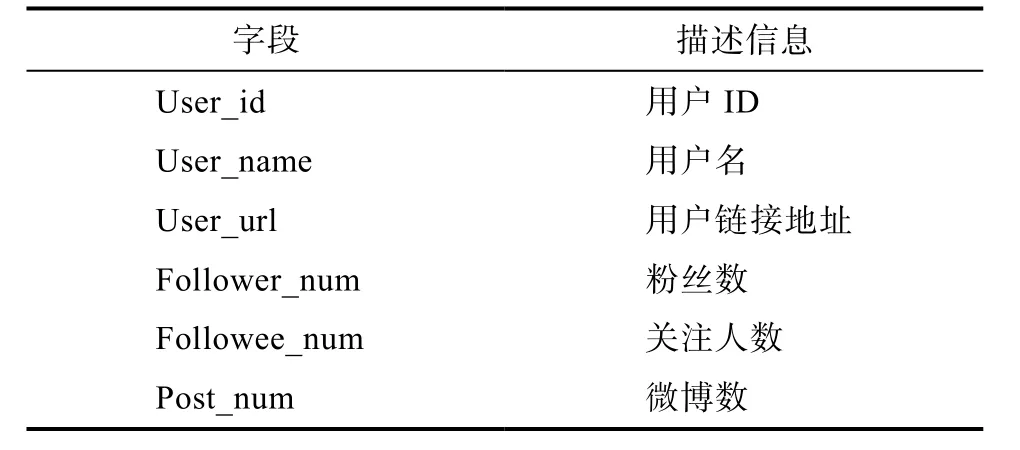
表5 微博用户模型Tab.5 Micro-blog user model

同时，获取每个用户的关注和粉丝信息如表6、表7所示。

除了爬取用户基本信息外，对每个用户，用另一个爬虫获取其前5页微博数据，并获取点赞数、转发数、评论数等信息，存储的数据如表8所示。

表6 关注关系Tab.6 Followee relationship

表7 粉丝关系Tab.7 Followwer relationship

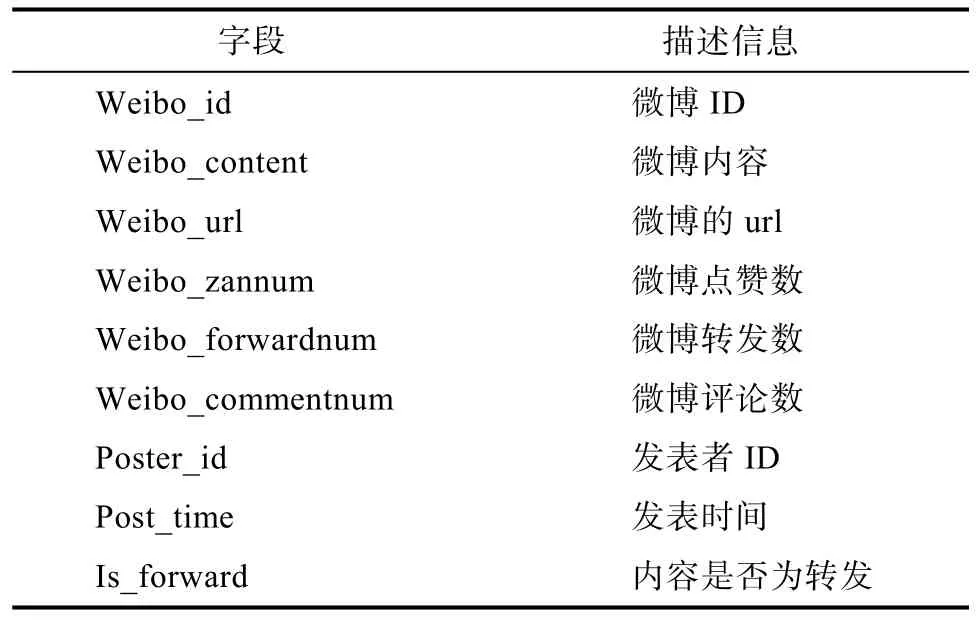
表8 微博数据Tab.8 Micro-blog data

基础数据抓取完毕后，对基础数据进行清洗和处理[11]，进一步完善用户模型，如下表9所示。其中，Follower_list为粉丝的ID列表，Followee_list为关注的ID列表，Crawl_postnum，Yc_post, Post_forwardnum，Yc_forwardnum由统计得出。

表9 微博用户模型Tab.9 Micro-blog user model

因新浪的反爬策略，爬取的粉丝不一定都在数据中，并且许多用户间关系在用户模型中无法体现，无法形成完整和封闭的传播网络，需要对数据进一步做预处理操作。首先我们对节点进行加边操作，具体步骤为：（1）取用户列表中的用户IDi，在IDi的Follower_list（Followee_list）中依次取出一个IDj；（2）在用户列表中找到IDj，若IDi不在IDj的Followee_list（Follower_list）中，则将IDi加入到该Followee_list（Follower_list）中，作为该节点的一条出度。当加边操作结束后，即可开始构建实验传播网络。将微博网络中的用户表示为试验网络中的节点，用户的关注和粉丝关系表示为节点间的有向边。例如，用户A关注B，则A为B的粉丝，在网络中生成一条由B指向A的有向边，作为消息传播方向；双向关注则添加双向有向边。

4.2 实验结果分析

1. 用户聚类分析

参照4.1中对簇特性的定义，对实验网络的用户进行聚类分析，其聚类结果信息如下表10所示。聚类之后，网络3个类别节点情况如下表10所示。

表10 用户聚类结果Tab.10 user clustering result

2. 影响力最大化分析

在进行算法性能测试时，所使用的计算服务器（虚拟化平台）硬件参数为：内存64G，CPU30核，硬盘50G。在改进的K-LT模型中，对用户进行了聚类分析，并对阈值θv和权重ω(u，v)参数进行了优化。选取不同的top-k节点，时间消耗情况如下图2中所示，通过分析可知，在未改进的KK算法中，随着选取节点数的增加，其计算时间大幅度增加，在K-KK算法中，随着k值的增加，其计算增长幅度较为平缓，远小于KK算法的增长幅度，相比较而言对不同的k其计算时间有大幅度效率提高。

5 小 结

图2 算法时间消耗情况对比Fig.2 Comparison of algorithm time consumption

本文针对社交网络中的传播影响力最大化问题，基于个体对信息要求差异和影响力差异两方面考虑，提出改进的K-LT模型和K-KK算法。在传播网络中，先对用户进行聚类分析，将用户划分到不同类别，对不同类别用户，考虑其对信息的需求不同，对其他用户产生的影响也不同，进而对影响力和接受信息阈值参数进行优化。在参数优化后，给出基于聚类的K-LT传播模型，以K-LT模型为基础，给出基于聚类的K-KK影响力最大化算法，实验结果表明，算法改进后，其计算效率有较大幅度提高。

[1] 宫秀文, 张佩云. 基于PageRank的社交网络影响最大化传播模型与算法研究[J]. 计算机科学, 2013, 40(S1): 136-140.

[2] Richardon M, Domingos P. Mining knowledge-sharing sites for viral marketing. Proceedings of the 8thACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Edmonton, Canada, 2002: 61-70.

[3] Kempe D, Kleinberg J, Tardos E, Influential nodes in a diffusion model for social networks. Cairel L, Italiano G F, Monteiro L, et al, eds. Automata, Languages and Programming. Libson, Portugal, 2005: 1127-1138.

[4] 蔡国永, 裴广战. 基于LT+模型的社交网络影响力最大化研究[J]. 计算机科学, 2016, 43(9): 99-102.

[5] Leskovec J, Krause A, Guestrin C, et al. Cost-effective outbreak detection in networks. Proceedings of the 13thACM SIGKDD International Conference on Knowledge Discovery and Data Mining. San Jose, USA, 2007, 420-429.

[6] Goyal A, Lu W, Lakshmanan L V. CELF++: Optimizing the greedy algorithm for influence maximization in social networks. Proceedings of the 20thInternational Conference Companion on World Wide Web. Hyderabad, India, 2001: 47-48.

[7] Chen W, Wang Y, Yang S. Efficient influence maximization in social networks. Proceeding of the 15thACM SIGKDD International Conference on Knowledge Discovery and Data Mining. Paris, France, 2009: 199-208.

[8] Chen W, Yuan Y, Zhang L. Scalable influence maximization in social networks under the linear threshold model[C]. 2010 IEEE 10th International Conference on Data Mining (ICDM). IEEE, 2010: 88-97.

[9] Kimura M, Saito K. Approximate solutions for the influence maximization problem in a social network. Gabrys B, Howlett R J, Jain L C eds. Knowledge-Based Intelligent Information and Engineering Systems. Bournemouth, UK, 2006: 937-944.

[10] Kempe D, Kleinberg J, Tardos E,Maximizing the spread of influence through a Social network[C]. Proceedings of the ninth ACM ISIGKDD international conference on knowledge discovery and data mining .ACM, 2003: 137-146.

[11] 蒙在桥. 在线社交网络的动态消息传播模型研究与应用[D]. 广东工业大学, 2014.

[12] 张振华, 刘瑞芳. 微博社交网络中面向机构的用户挖掘[J].软件, 2013, 34(1): 121-124.

[13] 李善涛, 肖波. 基于社交网络的信息推荐系统[J]. 软件, 2013, 34(12): 41-45.

[14] 张晨辰, 赵方. 社交网络服务系统核心功能的设计与实现[J]. 软件, 2013, 34(12): 92-98.

User Clustering based Social Networks Influence Maximization Propagation Model

ZENG Yan-qing1, CHEN Zhi-de2, LI Xiang-yu3
(1. Fujian Jiangxia University Fujian, Fuzhou 350108; 2. Fujian Normal University Fujian, Fuzhou 350007; 3. Minjiang Normal College Fujian, Fuzhou 350007)

This paper focuses on the problem of influence Maximization in social networks. On the basis of the classical Linear-threshold propagation model, we cluster and analyze the users in social networks. Then, we propose our improved K-LT propagation model. Based on K-LT model we further propose the K-KK influence maximization algorithm. The simulation is carried out by collecting the real social network data. The experimental results show that the improved K-KK algorithm is better than the other one when it is not improved.

Social networks; Propagation model; Influence maximization

TP393.09

A

10.3969/j.issn.1003-6970.2017.05.031

曾燕清，硕士学历。工作单位：福建江夏学院，电子信息科学学院，主要研究方向：社交网络，大数据，无线安全与隐私；陈志德，教授，博士学历，福建师范大学，数学与计算机科学学院。主要研究方向：网络与信息安全，社交网络，大数据；李翔宇，硕士学历，毕业学校于福建师范大学。主要研究方向：数据挖掘。工作单位：闽江师范高等专科学校，计算机系。

本文著录格式：曾燕清，陈志德，李翔宇. 基于用户聚类的社交网络影响力最大化传播模型[J]. 软件，2017，38（5）：144-149