非一致终端约束下火星大气进入段制导律设计
郭敏文,李茂登,黄翔宇,王大轶
(北京控制工程研究所,北京 100190)
非一致终端约束下火星大气进入段制导律设计
郭敏文*,李茂登,黄翔宇,王大轶
(北京控制工程研究所,北京 100190)
针对小升阻比的火星探测器在火星大气进入过程中所面临的难点问题,对火星大气进入过程制导方法进行了研究。首先在确知探测器弹道系数和升阻比的前提下,考虑过程量及开伞条件约束,优化设计再入飞行的初始再入角。然后考虑非一致终端约束和飞行器的有限机动能力,设计参考轨迹剖面,并确保其能提供足够的裕度来应付各种参数不确定性。最后设计标准轨道法制导律,完成轨迹有效跟踪,并通过六自由度仿真验证了算法的合理性,为火星着陆项目中大气进入段制导方案设计提供参考。
小升阻比探测器;非一致终端约束;初始状态设计;参考轨迹设计;大气进入制导
0 引 言
火星大气进入过程是指探测器从距离火星表面约120 km处的火星大气层上边界开始,至开伞点前的大气飞行过程,该阶段一般持续4~5 min。其减速控制主要通过实时调整倾侧角大小以改变升力方向,进而调整探测器飞行轨迹。
迄今为止,人类已经进行了49次火星探测的尝试,而其中成功率仅有47%,已有的16次着陆探测任务中只有7次成功,其中着陆过程技术故障是引起着陆任务失败的主要原因[1]。火星进入、下降和着陆是整个火星着陆过程中最为关键的阶段,该阶段的导航制导性能直接影响着陆任务的成败[2]。影响大气进入段制导性能的主要因素为探测器的构型参数和火星的大气条件。探测器的构型参数主要包括弹道系数和升阻比,它们均影响着制导性能,且与开伞条件(开伞点高度、马赫数和动压)密切相关。火星大气稀薄,密度约为地球大气的1/100,受季节影响随火星年变化很大,不同纬度地区大气密度也有很大的不同。在20 km高度以下大气稠密区,较地球大气环境也存在更大的不确定性(如图 1所示),这些都将直接影响开伞点的状态。
综上,弹道系数、升阻比的偏差以及火星大气环境的不确定性,都影响着制导效果,那么要实现在理想的开伞高度下满足探测器着陆的精度指标,就要求火星着陆器的制导系统具有较强的鲁棒性和一定的环境自适应能力。
目前,火星大气进入段制导方法的相关研究内容很多[3],包括:标准轨道法[4]、解析预测校正算法[5]、能量控制算法[6]和数值预测校正算法[7-8]等,这些算法均以倾侧角为控制量。文献[9]将上述进入制导方法主要分为两类:一类是预测制导法,另一类是标准轨道法。文献[10]将倾侧角调整方法分为理论EDL(entry,descent and landing)制导、解析预测校正制导和数值预测校正制导三类。Hamel[11]也类似地将制导方法分为标准轨道法、解析算法和数值算法三类:标准轨道法[12],是通过离线设计最优参考轨迹并进行存储,在制导过程中试图在每个时刻都保持这种最优性能使探测器按着标称轨迹飞行;解析预测校正算法[13]和能量控制算法,属于解析算法,这类算法主要通过某些假设来得到解析制导律;数值预测校正算法[14-15],是根据当前状态积分剩余轨迹来预测目标点的状态,从而利用偏差来实时校正倾侧角的指令值。
本论文针对火星大气进入所面临的难点问题,设计了火星大气进入过程制导方案,并完成相关6自由度仿真验证,为火星着陆项目中大气进入段制导方案设计提供参考。

图 1 地球大气摄动模型100 casesFig. 1 Earth atmosphere perturbation model for 100 cases and Mars atmosphere perturbation model for 500 cases
1 火星大气进入过程难点问题
1.1 动力学约束
探测器始终以配平攻角飞行[10];根据大气层再入飞行过程中探测器的受力情况,不考虑推力和控制力,则探测器三自由度再入质心动力学方程如式(1)所示。
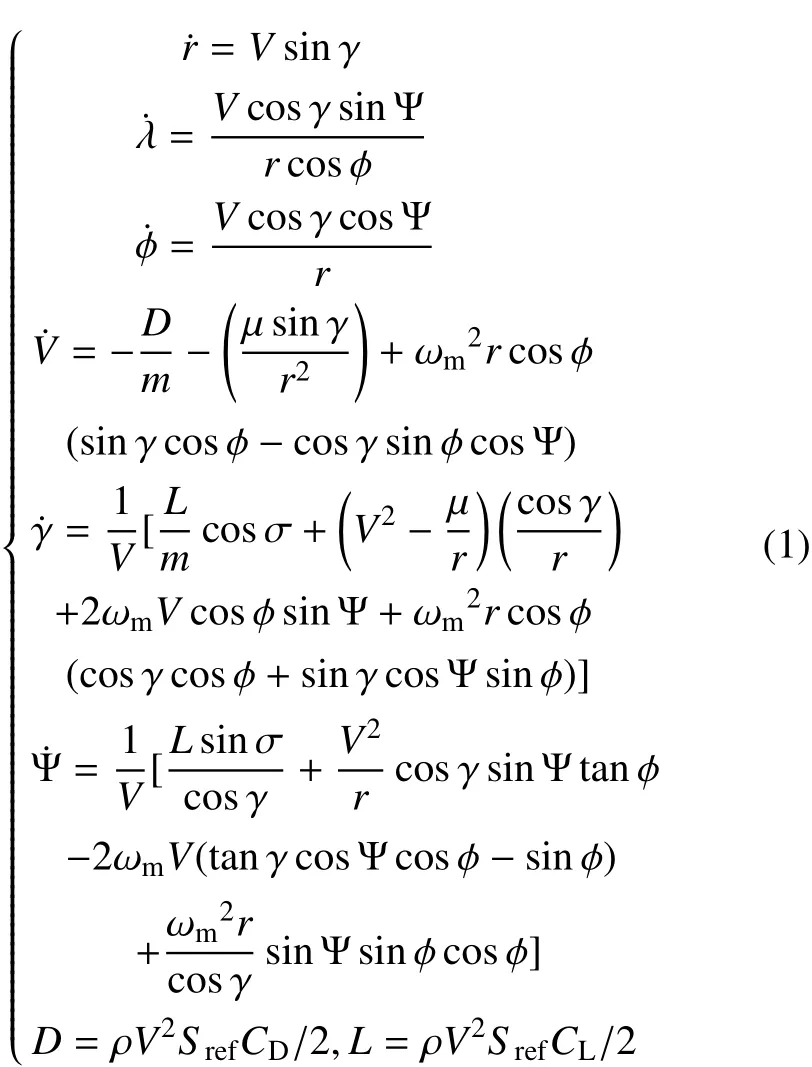
式中:ρ为火星大气密度;r为火心距,r = h + Rm;h为跳跃高度;V为探测器相对火星速度;火星平均半径Re;μ为引力常数;ωm为火星自转角速度;λ为经度;φ为纬度;γ为飞行路径角指飞行速度矢量与当地水平方向的夹角;Ψ为速度方位角,指某时刻飞行速度矢量与当地正北方向的夹角,顺时针为正;σ为倾侧角,从探测器内部来看,右侧为正;D,L分别为气动阻力和升力;CD,CL分别为阻力系数和升力系数;探测器最大横截面积为Sref;质量为m。
1.2 开伞条件约束
火星大气进入制导开伞条件约束相比位置偏差约束更强,即需要先满足开伞条件再考虑着陆精度问题。为了保证再入过程的安全,参考火星科学实验室(Mars Science Laboratory,MSL)的着陆任务,开伞时需要严格满足的约束条件考虑如下[16]:
1)开伞高度
由于降落伞减速后需采用避障动力减速系统,需要给操作预留足够的时间以确保安全着陆,所以提出最小的开伞高度为7 km。
2)马赫数
火星标准音速计算公式为

其中:km为绝对指数;取为1.29;Rm为气体常数;取为191.8 J/kg/K;Tm为热力学温度,当近火星表面热力学温度为241 K时,火星大气音速为244 m/s。开伞点处的马赫数直接影响两个物理量,气动热流和膨胀动力。马赫数不宜过高或过低,过高则驻点热流过高或导致激烈的膨胀使得降落伞无法承受,马赫数限制为1.4~1.8。
3)动压
充分的动压确保开伞膨胀。对MSL着陆系统,动压限制为250~850 Pa。
1.3 火星大气进入过程约束的不一致性
火星进入过程参考倾侧角剖面优化设计时的非一致终端约束为:最小化航程偏差、满足开伞的约束条件。当探测器弹道系数较大,或者着陆点处的大气很稀薄时,制导律的设计往往不能同时满足落点精度要求和开伞条件的约束。
1.4 火星大气进入过程制导能力较弱
火星大气环境恶劣,大气密度散布较大,需要火星探测器具有较大的升力以提供足够的控制能力来应对散布情况,从而提高着陆的精度。但火星大气稀薄,探测器升阻比较小,控制能力有限。因此如何设计制导律提供足够的裕度来应对各种环境散布是个难点问题。即在参数不确定的情况下,制导过程不至使倾侧角长时间饱和而失去减小航程偏差的能力。
2 参考轨迹设计分析
2.1 初始状态设计分析
初始状态设计分析这里指,在确知弹道系数和升阻比的情况下,合理地设计初始再入角。
弹道式再入探测器再入时所承受的最大过载、最大驻点热流和总吸热量主要受再入角的影响。再入角过大时,轨道过陡,最大过载和最大驻点热流会超出约束范围,因此存在一个最大的再入角。而再入角过小,由于飞行时间过长,会使总吸热量超过允许值,也有可能因为垂直速度分量过小,不足以使它继续深入大气层,而是在稠密的大气层的边缘掠过无法完成正常再入,因此也存在一个最小的再入角。
为实现成功再入所确定的再入角范围为再入走廊。这里为得到最佳初始再入角,假设再入角变化范围取值为-8~-15°,每隔0.1°做一次常值倾侧角剖面的再入仿真,记录再入高度变化曲线和过载的变化曲线,并记录固定2.0马赫数开伞时的高度和动压值,以及再入过程的过载峰值、热流密度峰值和总吸热量。最后选出使开伞高度最高且满足所有约束的初始再入角为最佳再入角。
2.2 参考轨迹设计
参考剖面优化设计的几个目的:1)最小化航程偏差。2)达到着陆点的同时需要满足开伞约束条件。3)标称倾侧角剖面在散布情况下需表现良好。4)在还未选定着陆点的时候,需尽量保证开伞点的高度最大。
设计的参考剖面提供足够的裕度来应付各种环境散布问题,同时需考虑飞行器的机动能力,即在存在不确定环境情况下,制导律不至使倾侧角饱和而失去减小航程偏差至收敛的能力。标称的倾侧角剖面的极限从大气密度及气动系数Cd的散布情况进行估计[17]
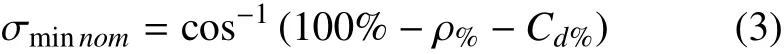
其中:典型的大气密度散布为25%;气动系数散布为10%;得到允许的最小初始倾侧角为49°;同理最大的倾侧角为131°。如果倾侧角标称剖面不能满足该范围约束,则应要求增大升阻比或者减小弹道系数。
在火星着陆时,当飞行器的弹道系数较大,或者选取的着陆点大气较为稀薄时,参考倾侧角的剖面设计为常值时往往会导致不能同时满足落点精度要求和开伞条件约束,因此需选择变化的参考倾侧角剖面来改善再入飞行性能。变参数剖面能提高裕度以满足散布仿真时的需求,减小低速飞行的倾侧角可延长在稠密大气层中的飞行时间。调研表明大多数可行的变值参考倾侧角剖面,一般在进入初始段时,升力在垂直面分量较小,倾侧角选择为70°或80°。然后倾侧角线性减小至前面分析设计的倾侧角最小值50°,如图 2所示。变值的倾侧角剖面可能会获得最大的高度下降速度0,以更好地平衡开伞高度和开伞位置。

图 2 轨迹规划采用的倾侧角剖面Fig. 2 The profile of the bank angle for trajectory planning
由于进入器飞行过程中是通过控制倾侧角来进行引导,可控变量单一,所以倾侧角剖面应相对简单,工程上倾侧角剖面通常采用分段常值或分段线性化等简化方式进行设计。
1)采用的倾侧角剖面为“线性 + 常值”的形式设计参考轨迹,如图 2所示。
2)为调节开伞点处航程偏差满足精度要求,采用牛顿迭代方法进行求解初始倾侧角值。
3)针对大气环境的不确定性,采用鲁棒分析方法确定末倾侧角值(50°)。
4)倾侧角的符号由3.2的1)部分逻辑确定。
3 制导律设计
3.1 纵向控制逻辑
再入终端点制导算法[18]设计主要分以下流程:
第一步,基于给定的倾侧角剖面形式在标称参数下通过积分动力学]方程设计参考轨迹x∗(t)=[[S∗(t), V∗(t),γ∗(t),h∗(t)T,各状态变量分别为纵程、相对速度、飞行路径角和高度。
第二步,反向积分动力学方程从tf到t0,得到计算增益所需的协态变量值
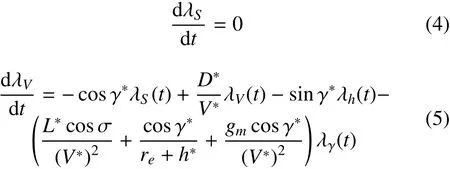
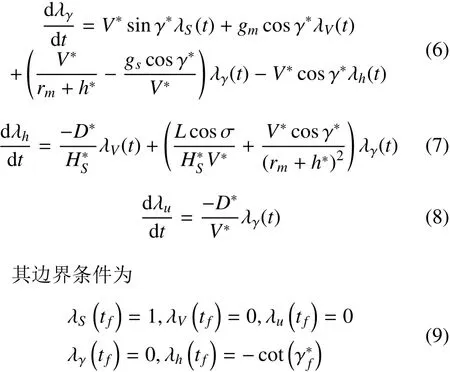
其中:gm为火星重力加速度;rm为火星半径平均高度;Hs为密度尺度高;λ(t)=[λS(t)λV(t)λγ(t) λh(t)]T为各状态变量的小偏差对航程偏差的影响系数向量,因此在任意时刻有航程偏差表达式为Rf=δλ(t)·δx(t)。针对在标称轨迹附近线性化得到的偏差动力学方程如式(10)所示,以状态小扰动为新的状态变量,控制小扰动为新的控制变量,
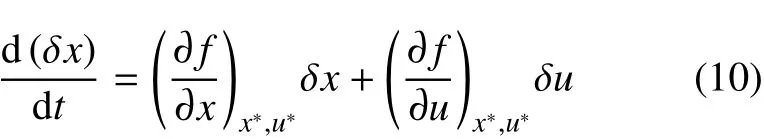
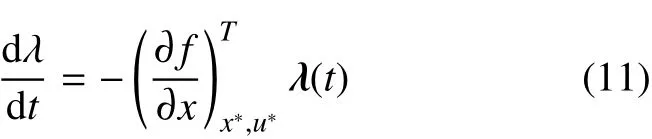
第三步,计算并保存以速度V为自变量的增益系数。
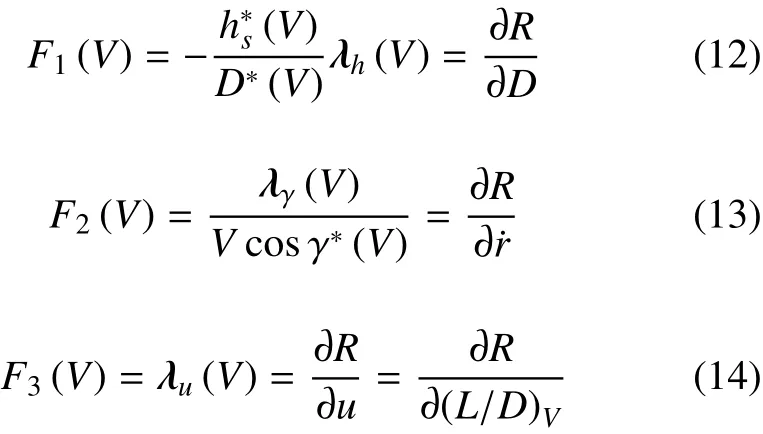
第四步,利用上面增益计算控制量

3.2 横程控制方案
1)横程控制的实现在一次反转后,横程偏差的限制采用速度的线性函数,直至速度降至1 100 m/s。如χc=c1V+c0,这里c1,c0的选取将针对不同的探测器,根据横程偏差的精度要求以及倾侧角反转次数的限制进行调整得到的,如图 3所示。
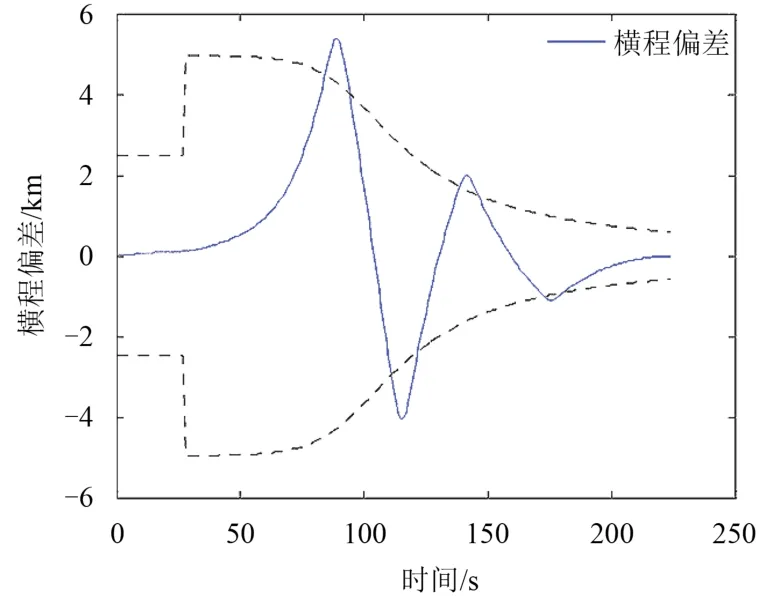
图 3 横程偏差随时间变化Fig. 3 Crossrange error time history
2)当速度小于1 100 m/s,轨迹进入低速段时,即使倾侧角调整为零度,也不能提供足够的升力去抬高飞行路径角以扩大纵程,但仍然可以有效地继续调节方位角的偏差。采用方位角调整逻辑(heading alignment logic)进行控制。
4 算例分析
4.1 六自由度仿真
火星探测器的相关参数参考NASA航天器设计标准《SURFACE MODELS OF MARS(1975)》。
再入点初始位置误差如表 1,以马赫数和动压条件作为开伞条件,仿真次数1 000次。仿真结果如图4~6所示。
为验证该算法的鲁棒性,同时考虑导航偏差完成了1 000种情况的蒙特卡洛仿真,偏差分布情况如表 1所示。图 4为距离理想着陆点的纵程与横程偏差散布情况,偏差3σ椭圆大小约为50 km × 10 km。图 5为各散布仿真开伞点处实际马赫数(这里实际值指真实动力学输出值而非导航值)与动压的关系,散布仿真时将马赫数等于2设定为开伞的判断条件,可见每次开伞点的动压均满足约束条件。同理图 6说明每次开伞时的高度均满足开伞的约束条件。

表 1 偏差分布情况(3σ)Table 1 Statistics of dispersions used in Monte Carlo simulations (3σ)
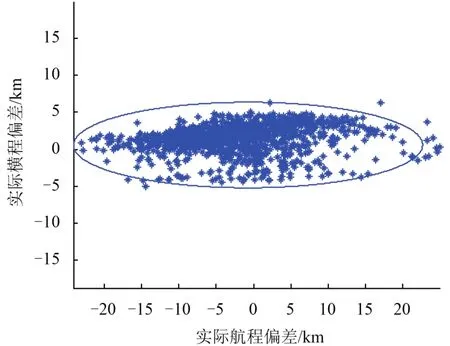
图 4 仿真结束时的实际航程和横程偏差Fig. 4 True value of downrange and crossrange errors at parachute deployment for 1000 cases
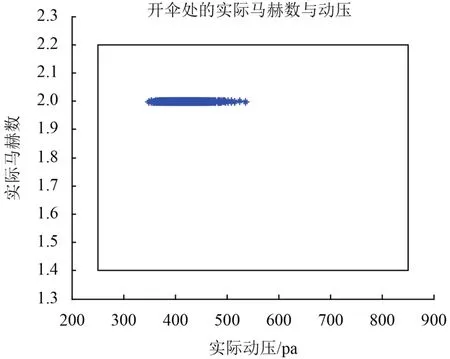
图 5 仿真结束时的实际马赫数与动压Fig. 5 True value of mach number and dynamic pressure at parachute deployment for 1000 cases

图 6 仿真结束时的实际马赫数与高度Fig. 6 True value of mach number and altitude at parachute deployment for 1000 cases
5 结 论
火星大气进入段是火星着陆过程中风险最大的阶段,该阶段的制导性能直接影响着陆任务的成败。本文对火星大气进入过程的制导方法进行了研究,并给出了在考虑各种约束情况下的详细的方案设计过程与原理。通过六自由度的仿真表明,该制导方案能有效地导引火星探测器在理想的开伞高度到达指定的着陆区域上空,且满足其他各开伞约束条件。
[1]崔平远,于正湜,朱圣英. 火星进入段自主导航技术研究现状与展望[J]. 宇航学报,2013. 34(4):447-456.
Cui P Y,Yu Z S,Zhu S Y. Research progress and prospect of autonomous navigation techniques for Mars entry phase[J]. Journal of Astronautics,2013,34(4):447-456.
[2]崔平远,高艾,于正湜. 火星着陆自主导航方案研究进展[J]. 深空探测学报,2014,1(1):18-27.
Cui P Y,Gao A,Yu Z S. Research progress of autonomous navigation scheme for Mars landing[J]. Journal Of Deep Space Exploration,2014,1(1):18-27.
[3]李爽,彭玉明,陆宇平. 火星EDL 导航、制导与控制技术综述与展望[J]. 宇航学报,2010,31(3):621-627.
Li S,Peng Y M,Lu Y P. Review and propect of Mars EDL navigation guidance and control technologies[J]. Journal of Astronautics,2010,31(3):621-627.
[4]Leavitt J A,Mease K D. Feasible trajectory generation for atmospheric entry guidance[J]. Journal of Guidance,Control and Dynamics,2007,30(2):473-481
[5]Thorp N A,Pierson B L. Robust roll modulation guidance for aeroassisted Mars mission[J]. Journal of Guidance,Control,and Dynamics,1995,18(2):298-305.
[6]Rousseau S. An energy controller aerocapture guidance algorithm for the Mars sample return orbiter[R]. Paper AAS 01-104,2001.
[7]Powell R W. Numerical roll reversal predictor corrector aerocapture and precision landing guidance algorithms for the Mars surveyorprogram 2001 missions[R]. AIAA Paper 98-4574,1998.
[8]Dierlam T A. Entry vehicle performance analysis and atmospheric guidance algorithm for precision landing on Mars entry vehicle performance analysis and atmospheric guidance algorithm for precision landing on Mars[D]. Cambridge:Massachusetts Institute of Technology,1990.
[9]赵汉元. 飞行器再入动力学和制导[M]. 长沙:国防科技大学出版社,1997.
[10]Davis J L,Cianciolo A D,Powell R W,et al. guidance and control algorithms for the Mars entry,descent and landing systems analysis[R]. NF1676L-10124,2010.
[11]Hamel J F,Lafontaine J d. Improvement to the analytical predictorcorrector guidance algorithm applied to Mars aerocapture[J]. Journal of Guidance,Control and Dynamics,2006,29(4):1019-1022.
[12]Tu K Y,Munir M S,Mease K D,et al. Drag-based predictive tracking guidance for Mars precision landing[J]. Journal of Guidance,Control,and Dynamics,2000,23(4):620-628.
[13]Kluever C A. Entry guidance performance for Mars precision landing[J]. Journal of Guidance,Control,and Dynamics,2008,31(6):1537-1544.
[14]Joshi A,Sivan K,Amma S S. Predictor-corrector reentry guidance algorithm with path constraints for atomospheric entry vehicles[J]. Journal of Guidance,Control,and Dynamics,2007,30(5):1307-1318.
[15]Kozynchenko A I. Predictive guidance algorithms for maximal downrange maneuvrability with application to low-lift re-entry[J]. Acta Astronautica,2009,64:770-777.
[16]Mendeck G F,Craig L. Mars science laboratory entry guidance[R]. NASA JSC,2011.
[17]Mendeck G F,Carman G L. Guidance design for Mars smart landers using the entry terminal point controller[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. California:AIAA,2002.
[18]Carman G L,Ives D G,Geller D K. Apollo-derived Mars precision lander guidance[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit. Boston:AIAA,1998.
电话:(010)68111192
E-mail: mwguo8500@163.com
On Guidance Algorithm for Martian Atmospheric Entry in Nonconforming Terminal Constraints
Guo Minwen*,Li Maodeng,Huang Xiangyu,Wang Dayi
(Beijing Institute of Control Engineering,Beijing 100190,China)
A method for Martian atmospheric entry guidance is researched in this paper,regarding the problems faced by Mars exploration vehicle with low lift-to-drag ratios. Firstly,with a certain ballistic coefficient and lift-to-drag ratios,the initial reentry angle is designed considering the process variable constrains and the parachute deployment constrains. Then the reference trajectory is developed for providing the sufficient margin to overcome the parameter uncertainties considering the nonconforming terminal constrains and the low control authority. Finally, the tracking guidance law is presented. The six degree of freedom simulation demonstrates the effectiveness of the approach,which provides references to the Mars exploration project.
vehicles with low lift-to-drag ratios;nonconforming terminal constraints;the initial state design;reference trajectory planning;atmospheric entry guidance
V448.2
A
2095-7777(2017)02-0184-06
10.15982/j.issn.2095-7777.2017.02.013
郭敏文(1985–),女,工程师,主要研究方向:航天器导航制导与控制。通信地址:北京海淀区中关村南三街16号(100190)
[责任编辑:宋宏,英文审校:朱鲁青]
郭敏文,李茂登,黄翔宇,等. 非一致终端约束下火星大气进入段制导律设计[J]. 深空探测学报,2017,4(2):184-189.
Reference format: Guo M W,Li M D,Huang X Y,et al. On guidance algorithm for martian atmospheric entry in nonconforming terminal constraints [J]. Journal of Deep Space Exploration,2017,4(2):184-189.
2015-10-06
2015-11-30
国家自然科学基金(61503023,61403030)

