基于Voronoi微观晶粒结构确定Fe-Si合金中硅的晶界扩散系数
徐勇强, 秦宗慧, 周海婷, 陈建钧
(华东理工大学机械与动力工程学院,上海 200237)
基于Voronoi微观晶粒结构确定Fe-Si合金中硅的晶界扩散系数
徐勇强, 秦宗慧, 周海婷, 陈建钧
(华东理工大学机械与动力工程学院,上海 200237)
铁基体中渗硅是生成高硅钢材料的主要方法,但现有的硅扩散过程分析往往只考虑整体的扩散效果,忽略了微观晶粒间与晶粒内的扩散差异。为了研究晶界对于扩散的影响,本文基于Voronoi图建立三维微观模型模拟了晶粒间与晶粒内的硅扩散行为。通过化学气相沉积实验、扫描电镜以及能谱元素分析测量计算得到材料微观结构参数和晶粒内的体扩散系数Dg。通过实验得到晶界宽度、晶粒尺寸等材料微观结构,在此基础上用有限元计算获得微观体积元中晶界的扩散系数Dgb。实验与模拟结果均表明硅在铁晶粒与晶界内的扩散存在明显差异,晶界扩散速率为3.3×10-3mm2/s,大致是体扩散速率的103~104倍,通过晶界扩散入基体的硅通量达到总通量的近三分之一,因此增大晶界体积分数对提高CVD渗硅效率和渗硅量有着重要作用。
晶界扩散; Fe-Si 合金; 有限元; Voronoi图
电工钢板是一种广泛应用于变压器、发电机等电力设备的材料。随着合金中硅质量分数的增加,硅钢片的电磁性能不断提升,具有高的电阻性,低的铁损率以及高磁导率。特别地,硅质量分数达到6.5%的Si-Fe合金具有几乎近于零的磁致伸缩性能。当材料中的硅质量分数增加到3.5%以上时,其延展性将会大幅降低,导致传统的冷轧或者热轧生产方式几乎无法生产[1-4]。因此,工业化高硅钢材料的制备常采用化学气相淀积法(CVD法),该方法在高温下将硅沉积于钢板表面,然后迅速向基板内部扩散[5-7]。硅分别在铁晶粒内部和晶界扩散,但是目前的研究往往不区分两者的差异,仅仅从整体考虑硅在铁中的扩散,尚未有实验将这种综合扩散分别考虑为体扩散和晶界扩散。晶界是最普遍的短途扩散通道,晶界中的扩散速度往往比体扩散速度快成千上万倍,然而,国内外对硅在铁中晶界扩散的研究非常欠缺。晶界扩散在金属和合金中的重要性已经引起了持续性的广泛关注[8-9],第一个晶界扩散定量模型是在1951年由Fisher[10]提出的,假设晶界扩散系数(Dgb)远大于体扩散系数(Dg)。Gibbs[11]发展了Fisher模型,在边界条件中考虑了晶界的线性隔离。如图1(a)所示,假设晶界为分布于晶粒间的具有均一厚度的快速扩散通道,在晶界上,原子可以沿Y轴快速渗入,同时可以沿着垂直于晶界的方向向晶粒内泄漏。晶界内元素往晶粒内的快速扩散将会导致扩散元素在临近晶界和远离晶界(离表面同一深度处)的浓度存在差异,Itckovich等[12]和Prokoshkina等[13]用相似方法研究钴和铁在铜中的晶界扩散,并分析了晶界表面张力梯度对晶界扩散的影响。
本文通过实验观察硅在铁晶粒内和晶界上的扩散差异,利用Voronoi图与有限元分析模拟相结合,研究了低硅钢板中硅的3D晶界扩散,最终计算出硅在铁晶界中的扩散系数。
1 实验过程
1.1 样品制备
当硅质量分数低于2.5%时,容易发生α-Fe和γ-Fe相变,影响渗透效率,所以实验样品选取硅质量分数为3.0%的低硅钢片,其晶粒平均尺寸为41 μm,化学组成成分见表1。裁剪试样为100 mm×60 mm ×0.3 mm,为了消除表面状况对实验的影响,实验前用粒度号W10~W5的砂纸进行抛光处理,然后在200~300 ℃中退火0.5 h以消除表面应力和损坏,随后在电子天平AB135-S上称取质量并记为m0。

表1 硅钢试样化学成分组成
1.2 CVD法渗硅
基于CVD法制备实验扩散偶,反应原理如下:
5Fe+SiCl4↑→Fe3Si+2FeCl2↑
(1)
实验前将样品置于高真空管式炉前端低温区,待中端炉温达到1 100 ℃时,将样品推送入高温区在炉中SiCl4和N2(体积比1∶3)氛围下进行反应150s(确保体扩散距离大于50μm以使测量点大于5个)。根据Mirani等[14]的研究,Fe3Si极薄层快速生成后,表层硅质量分数基本保持不变,而基板内部硅质量分数取决于硅的扩散速率。因此,只要保证反应过程中气氛充足,就可以形成表层硅质量分数为13.3%和基体硅质量分数为3.0%的铁硅扩散偶。达到反应时间后,迅速将样品推入低温区空冷至室温。取出试样在电子天平AB135-S上称量扩散后质量,记为m1。
1.3 EDS能谱测量
截取样品中间部分,沿平行于扩散方向的侧面抛光,然后用体积分数为3%的硝酸酒精溶液侵蚀显现晶界,使用扫描电子显微镜JSM-6360LV的EDS能谱分析对平行于扩散方向的横截面进行硅含量的定量分析,测量点分布如图1(b)所示,晶界上的测量点沿晶界从表面向基体内部延伸,晶粒内部测量点则远离晶界。电子光束的直径约为3 μm,保证了测量的精度。
1.4 体扩散系数
前人的研究表明硅在铁中的扩散符合Fick第二定律[14],把硅元素质量分数随渗透深度的变化曲线在软件Origin中拟合,公式如下:

(2)

图1 Fisher模型(a);EDS测量点分布图(b)Fig.1 Fisher model (a);EDS measuring point distribution (b)
式中,ws为表面硅质量分数,w0为基体初始硅质量分数,n0、n1为拟合常数。
Matano从实验得出的浓度曲线w(x)出发,得到不同浓度下的扩散系数D(w)的计算公式如下:
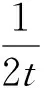
(3)
1.5 晶粒微观结构参数的测量
在材料晶粒图中随机分布10条平行于边界的直线(横向或纵向),计算每条直线上的晶粒平均截距(覆盖在一个晶粒上的测量线段的长度称为截距),取算术平均值作为晶粒平均直径[16]。其中,晶粒平均截距等于长度除以截到的晶粒个数。在图2(a)上随机选取横、纵向各5条直线,统计直线所截的晶粒截距,并计算其算术平均值。
利用金相分析软件JX-2000中的测微距模块在104倍率下的电镜图2(b)中测量晶界宽度,测量多处得到其晶界宽度平均值。
2 计算模拟
2.1 模型的建立
为研究硅通过晶界在铁基体中的扩散,本文基于 Voronoi图构建扩散模型进行有限元模拟。该模型可以实现3种类型的扩散:(1)只在晶体内部进行的体扩散;(2)只沿着无规律的多晶体之间的晶界进行的晶界扩散;(3)以上两种同时进行的更为复杂的扩散。Voronoi于1908年提出N维Voronoi方法的定义[17]:对于空间内的多个核点,某一区域内的点距某核点的欧几里德距离比距其他核点的更近,这一区域就称为该核点的Voronoi区域,空间内多个点的Voronoi区域共同组成了Voronoi空间结构。
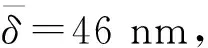
2.2 扩散模拟计算
模型的扩散计算过程是在ABAQUS中实现的,其计算扩散的条件满足如下假设:(1)晶界具有统一的厚度;(2)晶界内原子浓度在垂直于晶界方向上是恒定的,且流动只沿着平行于晶界的方向;(3)晶界扩散系数不随晶界内元素浓度变化而变化,而体扩散系数Dg随晶粒内元素浓度的变化而变化。如果假设平行于自由表面方向为x轴,垂直于自由表面方向为y轴,则在基体和晶界内的扩散方程分别如式(4)和式(5)所示:
(4)

(5)
式中,wb、wg分别为晶界内和晶粒内的硅质量分数;Dgb和Dg分别为晶界扩散系数和体扩散系数;t为时间;δ为晶界厚度;d为晶粒平均直径。
Lacaille等[19]在建立微观扩散体积元研究元素扩散总通量(φ)时发现:φ≈φg+φgb,φg为晶粒内的元素通量,φgb为晶界上的元素通量,当晶粒个数超过50时,该公式的误差将低于2%。建立如图3所示的有限元模型,其中图3(a)为二维Voronoi图,用于建立三维模型;图3(b)为Columnar模型,是由拉伸图3(a)得到的柱状晶结构,渗硅方向平行于模型拉伸方向;图3(c)所示Voronoi模型同样为Voronoi柱状晶结构,渗硅方向垂直于拉伸方向。边界条件设立为:(1)初始基体硅质量分数为3.0%;(2)上下两表面硅质量分数为13.3%。模型尺寸为0.3 mm×0.3 mm×2 mm (模型晶粒数量远超过50),采用稳态分析逐步迭代运算。

图2 微观晶粒结构图(a); SEM电镜下的三角晶界(b); ABAQUS模型中的三角晶界微观结构(c); 二维Voronoi微观结构图(d)Fig.2 Actual sample microstructure (a);Triangular GB by SEM (b);Triangular GB microstructure mesh in the Abaqus (c); 2D Voronoi microstructure(d)

图3 模型中的2D Voronoi图(a); Columnar柱状晶结构模型(b);Voronoi模型(c)Fig.3 2D Voronoi structure in model(a);Columnar crystal structure model(b);Voronoi model(c)
3 结果与讨论
3.1 实验结果
在反应式(1)中,当反应温度超过1 025 ℃时,FeCl2将变成气态随氮气排除,基板中的铁原子被硅原子置换出来,由于铁和硅原子质量的不同,将导致扩散前后基板质量变化。根据反应式(1)前后合金原子质量的关系,可得渗硅试验后基板硅质量分数计算公式如下:
wSi=(0.366m0-0.336m1)/m1
(6)
因为EDS分析的测量区域直径约为3μm,所以测量得到的晶界附近和晶粒内部的硅质量分数均为平均硅质量分数。表2列出了EDS随渗透深度变化的硅质量分数。远离晶界处的基体中硅质量分数几乎不受晶界往晶粒内快速扩散的影响,因此可以看成是硅在基体中体扩散的结果[12],而晶界及其附近由于受到晶界扩散的影响,所以测得的平均硅质量分数不能作为晶界内部的含量。将表2中的数据在Origin9.6软件中拟合,如图4(a)所示,晶粒内硅质量分数随深度变化的规律符合Fick第二定律,晶界附近平均硅质量分数明显高于晶粒内部。
将表2数据代入式(3)~(4),在MATALB中计算得到不同硅质量分数下的扩散系数Dg,变化范围为4.48×10-7~35.4×10-7mm2/s,见图4(b),Batz[20]在硅质量分数4.5%~7.2%范围内得到Dg为8.11×10-7~10.4×10-7mm2/s,Mitani等[14]发现硅质量分数为7%的硅钢中硅的扩散系数为16.3×10-7mm2/s,对比数据可知,以上实验数据与其他文献数据基本在同一数量级。
3.2 模拟结果
如图5(a)模拟结果所示,模型内的硅质量分数随渗透深度增加而降低,同时,在离表面同一深度处,硅质量分数从晶界处至晶粒内部逐渐降低,晶界上的硅质量分数并不远远高于晶粒内部,这表明在晶界扩散速率大的情况下,表面硅原子首先通过晶界纵向扩散,然后大量从晶界边缘向晶粒内部扩散,从而使得晶界内硅的质量分数不至于过大而且并不与深度呈线性关系。
由以上公式可知,清洁机器人的吸附稳定条件为:吸附力系合力P与重力G合力的作用锥δ<θ时,清洁机器人没有下滑趋势;当α≤β时,机器人没有翻倒趋势,或者当α> β时,翻倒力矩小于附着力矩。清洁机器人的吸附稳定条件用公式表示为:θ时,清洁机器人没有下滑趋势;当α≤β时,机器人没有翻倒趋势,或者当α

表2 硅含量在晶界附近和基体中沿渗透方向的分布

硅原子扩散入模型中的总通量φ可以在计算结果中得到,除以模型的总体积可获得模型中的平均硅质量分数。晶界扩散系数Dgb以1×10-4mm2/s的增量逐渐增加直到模型中的最终平均硅质量分数与实验测量值相吻合。如图5(b)所示,随着晶界扩散系数的增加,模型中的平均硅质量分数单调递增,当Dgb=3.3×10-3mm2/s时,模型中的平均硅质量分数达到实验值,此时的模拟晶界扩散系数符合实际扩散情况。最终晶界扩散系数确定为3.3×10-3mm2/s,大约是体扩散系数的103~104倍,表明晶界起到了快速扩散通道作用。

图5 晶界、晶界附近和晶粒内硅质量分数模拟结果(a); 模拟晶界扩散系数与实验中硅平均质量分数(b)Fig.5 Silicon mass fraction of grain boundary,near grain boundary and inner grain(a);Simulation of grain boundary diffusion coefficient and experimental silicon average mass fraction(b)
3.3 硅在铁基体中的扩散机制

3.4 晶界扩散对CVD渗硅的影响
硅原子扩散入模型中的总通量φ、通过基体扩散的通量φg和通过晶界扩散的通量φgb可以通过模拟计算得到,表3分别列出了晶界扩散系数为零和不为零时的模型平均硅质量分数,以及基体和晶界在两种情况下的通量占总通量的百分数。通过对比晶界扩散系数为零和不为零的模型平均硅质量分数可知,当晶界扩散不存在时,平均硅质量分数下降了0.596%;通过晶界扩散的硅通量占总通量的近三分之一。因此,晶界是CVD渗硅中的快速扩散通道,沉积在基体表面的硅元素可以通过晶界迅速向基体晶粒内部扩散。

表3 基体与晶界扩散通量占总通量分数及晶界体积分数
3.5 晶界体积分数对CVD渗硅的影响
晶界体积分数是材料中晶界体积占总体积的百分数,其数值与晶粒大小和晶界宽度有关。如表3所示,虽然晶界体积只占总体积的0.055%,但通过其扩散入基体的硅通量却达到总通量的将近三分之一。因此,增大晶界体积分数可以增多快速扩散通道从而促进元素扩散,减小材料平均晶粒度,增大晶界宽度对促进扩散有着重要意义。Baudouin等[23]运用铜极板快速加热方法,使得硅钢在400~800 ms内达到CVD实验温度而材料晶粒大小却不发生变化。刘刚等[24]和莫成刚等[25]运用异步轧制和表面研磨的工艺使无取向低硅钢表面晶粒大小达到10 nm,运用CVD法进行渗硅实验,样品渗硅深度由17 μm提高到51 μm,极大地提高了渗硅量。进一步的研究可以围绕开发新型工艺以增加材料晶界体积分数的方向开展,并将其应用入CVD增硅实际生产中。
4 结 论
本文将硅在铁基体中的扩散分为晶界扩散和体扩散进行精确分析,在硅扩散实验的基础上,采用基于Voronoi图建立的三维微观晶粒模型对硅扩散过程进行数值模拟。
(1) 硅在铁基体晶粒内部的扩散符合Fick第二定律,体扩散速率大小与硅质量分数有关。
(2) 离基体表面同一深度处,晶界附近硅质量分数明显高于晶粒内部,表明晶界扩散快于体扩散。经计算得到晶界扩散速率为3.3×10-3mm2/s,大致是体扩散速率的103~104倍。
(3) 模型中,晶界体积占总体积的0.055%,通过晶界扩散入模型的硅通量却占总通量的近三分之一,表明晶界是CVD渗硅中的快速扩散通道,增大晶界体积分数对提高渗硅速率和渗硅量有着重要作用。
[1] PHWAY T P P,MOSES A J.Magnetostriction trend of non-oriented 6.5% Si-Fe[J].Journal of Magnetism & Magnetic Materials,2008,320(20):611-613.
[3] SAENGDEEJINNG A,CHEN Y,SUZUKI K,etal.First-principles study on the dilute Si in bcc Fe:Electronic and elastic properties up to 12.5% Si[J].Computational Materials Science,2013,70:100-106.
[4] KASAMA A H,BOLFARINI C,KIMINAMI C S,etal.Magnetic properties evaluation of spray formed and rolled Fe-6.5% Si-1.0% Al alloy[J].Materials Science & Engineering A,2007,449/451(12):375-377.
[5] 杨劲松,谢建新,周成.6.5%Si高硅钢的制备工艺及发展前景[J].功能材料,2003,34(3):244-246.
[6] HAIJI H,OKADA K,HIRATANI T,etal.Magnetic properties and workability of 6.5% Si steel sheet[J].Journal of Magnetism & Magnetic Materials,1996,160(7):109-114.
[7] OK Y W,KIM S H,SONG Y J,etal.Structural properties of nickel silicided Si1-xGex(001) layers[J].Semiconductor Science & Technology,2004,19(2):285-290.
[8] HERZIG C,DIVINSKI S V.Grain boundary diffusion in metals:Recent developments[J].Materials Transactions,2003,44(1):14-27.
[9] DIVINSKI S V,BOKSTEIN B S.Recent advances and unsolved problems of grain boundary diffusion[J]// Defect and Diffusion Forum,2011,309-310:1-8.
[10] FISHER J C.Calculation of diffusion penetration curves for surface and grain boundary diffusion[J].Journal of Applied Physics,1950,22(1):74-77.
[11] GIBBS G B.Grain boundary impurity diffusion[J].Physica Status Solidi,1966,16(1):27-29.
[12] ITCKOVICH A A,BOKSTEIN B S,RODIN A O.Bulk and grain boundary diffusion of Co in Cu[J].Materials Letters,2014,135:241-245.
[13] PROKOSHKINA D,RODIN A O,ESIN V.About Fe diffusion in Cu[J].Defect and Diffusion Forum,2012,313-325:171-176.
[14] MIRANI H V M,MAASKANT P.Diffusion of Si in Fe/Si Containing 8% to 11% Si[J].Physica Status Solidi:A.Applied Research,1972,14(2):521-525.
[15] STRAUMAL B,RABKIN E,GUST W,etal.The influence of an ordering transition on the interdiffusion in Fe-Si alloys[J].Acta Metallurgica Et Materialia,1995,43(5):1817-1823.
[16] RADHAKRISHNAN B,ZACHARIA T.Simulation of curvature-driven grain growth by using a modified monte carlo algorithm[J].Metallurgical and Materials Transactions A,1995,26(1):167-180.
[17] AURENHAMMER F.Voronoi diagrams——A survey of a fundamental geometric data structure[J].Acm Computing Surveys,1991,23(3):345-405.
[18] MISTLER R E,COBLE R L.Grain boundary diffusion and boundary widths in metals and ceramics[J].Journal of Applied Physics,1974,45(4):1507-1509.
[19] LACAILLE V,MOREL C,FEULVARCH E,etal.Finite element analysis of the grain size effect on diffusion in polycrystalline materials[J].Computational Materials Science,2014,95:187-191.
[20] BORG R J,LAI D Y F.Diffusion inα-Fe-Si alloys[J].Journal of Applied Physics,1970,41(13):5193-5200.
[21] HARRISON L G.Influence of dislocations on diffusion kinetics in solids with particular reference to the alkali halides[J].Transactions of the Faraday Society,1961,57(57):1191-1199.
[22] BELOVA I V,MURCH G E.Phenomenological aspects of grain boundary diffusion[J].Defect & Diffusion Forum,2006,258/260:483-490.
[23] BAUDOUIN P,BELHADJ A,HOUBAERT Y.Effect of the rapid heating on the magnetic properties of non-oriented electrical steels[J].Journal of Magnetism & Magnetic Materials,2002,238(2):221-225.
[24] 刘刚,莫成刚,沙玉辉,等.表面纳米化硅钢薄带的低温渗硅与参数的影响[J].材料研究学报,2015,29(5):359-364.
[25] 莫成刚,黄凯,刘刚,等.表面机械研磨/异步轧制无取向硅钢薄带的渗硅行为[J].材料与冶金学报,2011,10(3):216-219.
Determination of Fe-Si Alloy Grain Boundary Diffusivity of Silicon Based on Voronoi Grain Microstructure
XU Yong-qiang, QIN Zong-hui, ZHOU Hai-ting, CHEN Jian-jun
(School of Mechanical and Power Engineering,East China University of Science and Technology,Shanghai 200237,China)
Silicon diffusing into iron base alloy is the main way to generate high silicon steel materials,however,the accurate analysis of silicon diffusion process is often considered as a whole diffusion effect,ignoring the microscopic diffusion differences in the grain and grain boundary(GB).In order to study the effects of grain boundaries for diffusion,a 3D microscopic model based on Voronoi structure is applied to simulate the process of intergranular and GB diffusion.The body diffusion coefficient (Dg) in the inner grain and material microstructural parameters can be provided by chemical vapor deposition(CVD) experiment,scanning electron microscopy(SEM) and energy spectrum analysis(EDS).Based on the material microcosmic parameters including grain boundary width and grain size,grain boundary diffusion coefficient (Dgb) of micro representative volume element can be obtained.The results of the experiment and simulation effectively show Silicon diffusion in Fe grain and grain boundary have obvious differences.TheDgbvalue is 3.3×10-3mm2/s,roughly 103~104times as high asDg.The silicon flux through grain boundary diffusion into alloy is reached nearly a third of total flux,so increasing the volumetric fraction of grain boundary can play an important role in improving efficiency and silicon quantity of CVD siliconizing.
boundary diffusion; Fe-Si alloy; finite element; Voronoi diagram
1006-3080(2017)03-0436-07
10.14135/j.cnki.1006-3080.2017.03.021
2016-10-18
徐勇强(1993-),男,江西丰城人,硕士生,研究方向为高硅钢生产工艺。E-mail:nafengyijiuxuxu@163.com
秦宗慧,E-mail: zhqin@ecust.edu.cn
TG732;TP393
A

