随机斑块饱和孔隙介质模型研究
未 晛
(中国石油天然气股份有限公司勘探开发研究院,北京100083)
随机斑块饱和孔隙介质模型研究
未 晛
(中国石油天然气股份有限公司勘探开发研究院,北京100083)
为研究介观尺度下斑块饱和对地震波传播规律的影响,对随机斑块饱和孔隙介质模型(Continuous Random Model of Patchy Saturation,简称CRM)进行了研究并提出改进模型MCRM。利用MCRM模型研究了介观尺度下气、水两相流体非均匀饱和时纵波速度频散和衰减特征,并对实验测量的数据进行了模拟分析。结果表明:①MCRM与CRM模型的纵波速度高低频极限相同且具有相同的衰减峰值,但前者特征频率增大,衰减曲线收窄;②MCRM与White模型有相同的高、低频极限,但MCRM模型的频散曲线变化相对缓慢、衰减峰值稍小;③利用MCRM模型能够模拟渗透率、含水饱和度、频率等参数对速度频散和衰减的影响,并能解释实验室测量的高、低孔隙度砂岩频散、衰减数据。该研究成果有助于更好地理解岩石的黏弹性行为,提高定量地震解释的精度。
随机斑块饱和;孔隙介质;纵波频散特征;统计特征;敏感参数
岩石孔隙中流体的流动是地震波衰减和速度或弹性模量频散的重要原因,并且其影响随着孔隙流体组分及其在岩石中的分布变化而变化。特别是在部分饱和岩石中斑块分布的流体区域之间,流体的流动会加剧地震波的衰减和速度频散,且该现象常发生在地震 测井频段,进而制约着地震定量解释精度的提高。因此,如何表征部分饱和流体在岩石中的分布状态及其对岩石弹性性质的影响成为地球物理领域的研究重点之一[1-6]。
国内外地球物理学家从理论上对流体的部分饱和如何影响地震波弹性性质做了大量的研究工作,结果表明,介观尺度上斑块分布的流体流动是造成地震波速度频散和衰减的重要原因,而岩石的微观孔隙结构和流体饱和方式严重影响着流体的分布情况[7-11]。WHITE等最先建立了介观尺度下非均匀孔隙岩石的流体流动模型[12-13],该模型是一种内部包含气泡的部分水饱和孔隙模型,被称为斑块饱和模型(Patchy Saturation Model,PSM),展示了部分饱和对于相速度频散和衰减的影响。当地震波通过部分饱和流体岩石时,会在内部气泡和外层水之间产生压力梯度,为达到力学平衡,流体发生流动,进而导致地震波的速度频散和衰减。DUTTA等指出了White模型的低频缺陷并完善了White模型[14]。JOHNSON通过引入斑块的比表面,将斑块模型气体充填于球形孔隙的假设推广到更为一般的孔隙形状下[15]。PRIDE等提出了双孔双渗模型,该模型和JOHNSON模型产生的模拟结果类似[16-17]。巴晶等进一步将此机制发展到包含不同流相和固相物质的部分饱和孔隙介质模型[18]。刘炯等利用不同斑块饱和模型研究了地震波的衰减和频散特征[19]。这些方法在某种意义上都假设流体是规则分布的,而在真实岩石中流体是具有不同形状、尺寸并且按照一定规律进行分布的。实验表明,斑块的形状依赖于实验过程,且与岩石的非均质性密切相关[8,20-22]。为了更准确地刻画斑块分布及其对地震波速度的影响,GUREVICH等首次提出了一维随机分布的流体非均匀饱和孔隙介质模型[23],M LLER等改进了一维随机斑块饱和模型,将此模型从一维扩展到三维[24-26],提出了一种普适的三维随机孔隙介质模型。TOMS等利用该模型研究了随机斑块饱和介质地震波衰减问题[3]。该模型可以较好地刻画孔隙流体在岩石中的赋存状态及其对地震波速度的影响,但是对模型有限性造成的误差以及岩石弹性参量统计特征信息的岩石物理基础有欠考虑。
在前人研究的基础上,本文首先给出随机斑块饱和孔隙介质模型的一种新算法,并对离散波数域中自相关函数计算时生成的误差进行了分析及有效处理;然后通过数值模拟计算,分析了多种不同流体饱和分布状态下的岩石弹性性质;最后对实验测量数据进行了模拟分析。
1 随机斑块饱和孔隙介质模型
1.1 理论基础
非均匀饱和模型通常假设流体具有固定形状和大小(如半径一定的球体),进而计算孔隙流体对地震波弹性性质的影响。而在真实岩石中,流体分布具有不同形状、尺寸,并且有一定规律。图1为某砂岩样品水驱气过程中水随时间变化在岩石中的分布情况,蓝色为背景,浅色代表水。这些形状不同且具有一定范围的区域其弹性性质也存在差异,地震波通过这些区域时会产生压力梯度,进而产生流体流动,造成频散和衰减现象。
为了刻画这些具有不同形状、一定分布范围的孔隙流体对岩石弹性参数的影响,TOMS等[3]、M LLER等[25-26]基于Biot方程、利用统计平滑的方法提出了一种普适的三维随机斑块饱和孔隙模型(简称CRM)。该模型可用于刻画斑块分布的孔隙流体流动诱发的频散和衰减现象。
根据CRM模型,地震波的纵波模量计算公式如下:
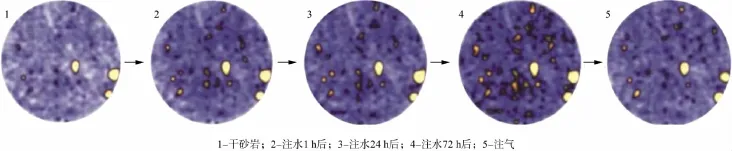
图1 某砂岩样品中孔隙流体在不同时刻的分布情况(修改自文献[8])
式中:H0表示背景介质纵波模量;Δ1和Δ2是无量纲的数,满足,代表Biot慢波的波数;B(r)表示相关函数。其中,Pd和H分别代表背景介质干燥和饱和流体的P波模量;ω为圆频率;κ0为背景渗透率;η为孔隙流体的粘滞系数;σXY为变量X和Y的相关系数,X和Y可取H,C和G。H=Pd+α2M,M=[(α-φ)/Kg+φ/Kf]-1,α=1-Kd/Kg,N=MPd/H,C=αM。α为Biot系数;φ为背景孔隙度;Kg,Kd,Kf和G分别代表固体相的体积模量、干燥岩石体积模量、孔隙流体的体积模量和岩石的剪切模量。
地震波速度的计算公式如下:
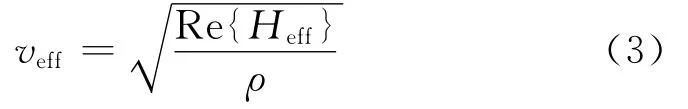
式中:ρ表示岩石密度。
地震波的衰减信息计算公式如下:

Heff中(公式(1))Δ2与频率无关,是随机场H,C和G的加权求和;积分项与频率有关,代表流体流动的作用[2627]。该模型计算过程中需要已知岩石骨架体积模量、颗粒体积模量、岩石剪切模量和孔隙流体体积模量的统计特征(方差或协方差),这些特征往往直接设定。同时,理论上的随机斑块饱和孔隙介质模型统计特征是在连续无限区域推导得到的,而实际模拟和计算必须在有限、离散介质模型中进行,这一矛盾会导致模拟和估计结果不精确。一般而言,在模型尺寸固定的情况下,描述统计特征的自相关长度越大,误差越大。
1.2 随机孔隙介质模型算法改进
基于对CRM模型的分析,本文给出了一种具体的模型参数确定方式:利用x-CT扫描图统计分析出岩石骨架、孔隙的统计性质。先借助阈值分割技术将x-CT灰度图中的孔隙和岩石基质分离,然后用具有一定统计规律的分布函数来描述。图2为某砂岩样品x-CT扫描的灰度图,灰度值范围为0~254,可清晰地分辨出岩石的颗粒和孔隙。图3显示了该砂岩样品孔隙与岩石骨架灰度(对应岩石密度)的概率密度分布。图4为数据回归分析得到的岩石孔隙和骨架灰度直方图,满足正态分布规律。
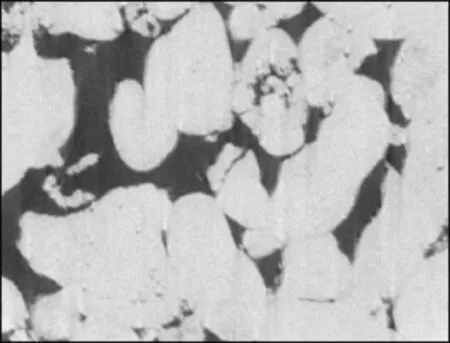
图2 某砂岩样品x-CT灰度扫描结果
x-CT灰度图反映了岩石密度信息,为了说明岩石弹性模量与密度的关系,用常见造岩矿物密度与弹性模量进行交会分析(图5)。由图5可见,密度与岩石的体积模量和剪切模量具有良好的线性关系。所以,由岩石密度的概率密度分布函数可以推导出岩石弹性模量的概率密度分布函数,从而得到岩石骨架和孔隙的统计学特征,这是获得随机斑块饱和孔隙介质模型各弹性参数的物理基础。尽管如此,岩石整体弹性性质仍受胶结、重结晶等地质作用及地区差异的影响,岩石骨架性质与矿物弹性性质仍存在差别,这是CRM模型下一步研究的一个方向。
此外,在CRM模型建立过程中,模型有限性与连续无限介质假设之间的矛盾不可避免,必需考虑这种有限性对计算结果精度的影响。添加锥形函数是
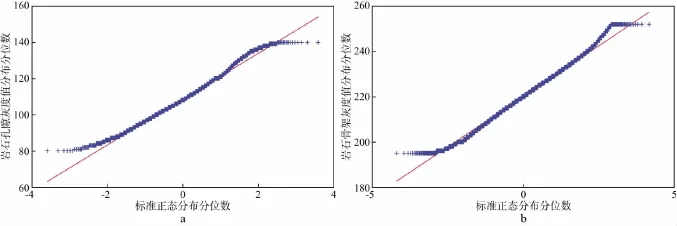
图4 岩石孔隙(a)和岩石骨架(b)灰度值与标准正态分布的回归分析
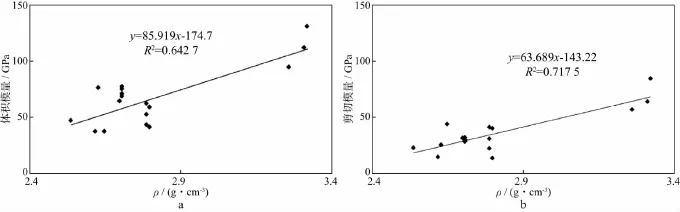
图5 造岩矿物体积模量(a)和剪切模量(b)与密度的关系
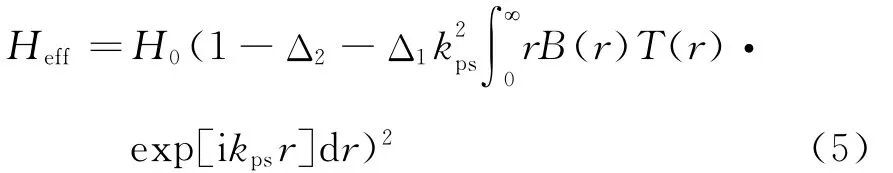
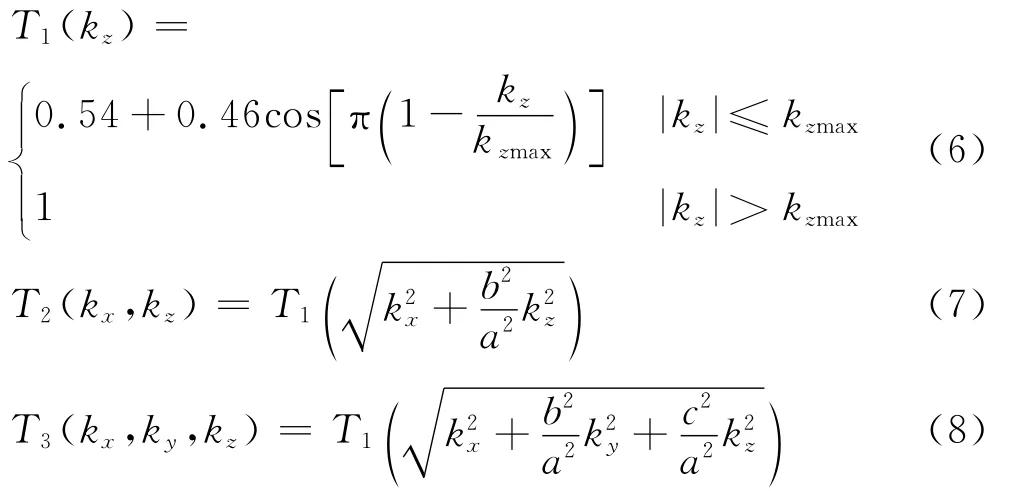
式中:T(r)是为压制模型有限性计算误差进行的修正。T(r)在频率域内一维、二维和三维情况下的表达式分别为:一种有效压制这种有限性计算误差的方法,锥形函数作用在模型各参数的随机场上,能有效压制这种计算误差,确保随机介质模型的可信度[27-29]。
改进后的随机斑块饱和孔隙介质模型(简称MCRM)纵波模量的计算公式如下:
式中:a,b和c分别为自相关长度因子;kzmax表示锥形函数的长度。
图6显示了锥形函数对二维岩石骨架随机模型的压制效果,模型选取500×500网格,岩石骨架平均模量为23GPa。图6a是没有加入锥形函数的二维随机模型,图6b为压制离散误差的结果。由图6可以明显看出锥形函数对剧烈扰动的压制效果,即扰动程度明显降低,模型更为平滑。一维情况下锥形函数对扰动的压制效果参见文献[27-29]。
1.3 MCRM模型计算步骤
本文在前人工作的基础上,结合基于CT扫描的模型参数确定方式,给出了MCRM模型的计算步骤:
1)对岩样进行预处理,由预处理后的岩样分析数据得到岩样的弹性参量统计特征信息,如Kd, Kg,Kf,G的方差和均值K珡,d珡Kg,珡Kf,珚G及其分布规律(如,正态分布、指数分布等);
2)基于岩样弹性参量的统计特征信息,构建Kd,Kg,Kf,G的随机场;
3)基于Kd,Kg,G的统计特征计算出Kd,Kg,G之间的协方差,直接利用相关系数公式进行计算,其中Kd,Kg,G之间完全相关,Kf与Kd,Kg,G均不相关,即固体相参数之间完全相关,流体与固体相参数不相关;
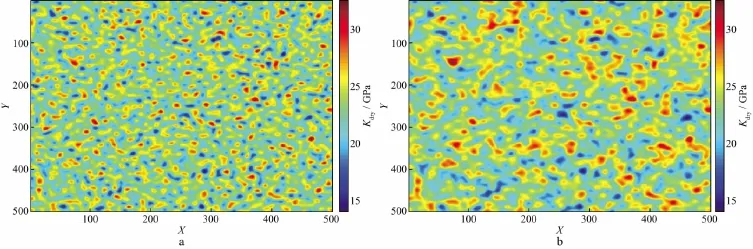
图6 锥形函数对二维岩石骨架随机模型压制的效果
4)利用H,C与Kd,Kg,Kf,G的关系得到H,C的随机场,H=Pd+α2M,C=αM,Pd为干燥岩石的P波模量,Pd=Kd+4G/3,M=[(α-φ)/Kg+φ/Kf]-1,α=1-Kd/Kg;
5)利用H,C和G的随机场得到H,C和G的方差和协方差,代入公式(2)至公式(5)得到岩石的频散和衰减信息。
2 算例及分析
2.1 MCRM与CRM的比较
首先比较CRM和MCRM的差异,模型参数参考文献[2-3],表1给出了CRM和MCRM采用的背景介质和孔隙流体参数。相关函数采用指数函数形式,即B(r)=exp(-|r|/a)。其中a为相关长度,例如非均质体的特征长度。假设干燥岩石骨架模量、颗粒模量和剪切模量的随机扰动都是完全相关的,而孔隙流体体积模量与其完全无关和在二维情况下,MCRM模型和CRM模型数值模拟的对比结果如图7所示,fc为Biot临界频率,自相关长度a=b=0.1m。当锥形函数为T=1时,改进的MCRM模型退化成CRM模型,此时两者的纵波速度和衰减Q值具有相同的结果(图7a和图7b)。考虑模型有限性的影响后(T≈0.17),MCRM和CRM模型的高低频极限速度基本相同,但MCRM临界频率变大,1/Q变窄且向高频方向移动(图7c,图7d)。
2.2 MCRM与White模型的比较
对MCRM和White模型进行了对比分析,表2为采用的孔隙介质和流体参数。孔隙介质为空气 水两相饱和,气体所占比例为0.35,其余为水充填。White模型中规则球体为水包气的圆球体结构,包裹体外径为0.1m。MCRM模型中相关函数采用指数函数形式,B(r)=exp(-|r|/a)。其中a为相关长度,例如非均质体的特征长度。TOMS等建立了相关长度a与流体饱和度S1,S2,体积比sv=r2i/R3c的关系,其中ri,Rc分别是规则球体的内径和外径[3]。
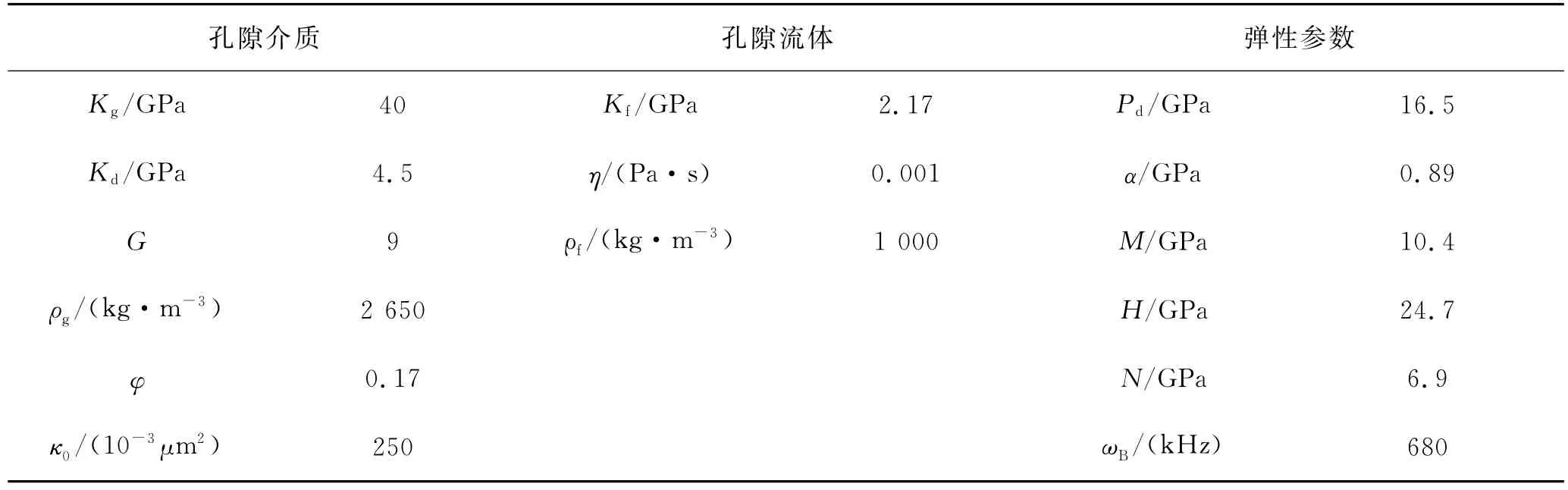
表1 CRM模型和MCRM模型参数[2-3]
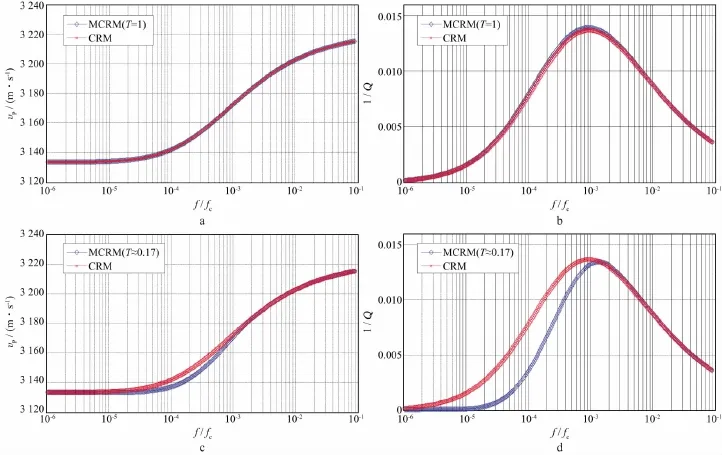
图7 T=1(a,b)和T≈0.17(c,d)时MCRM模型和CRM模型速度频散曲线与衰减(1/Q)对比
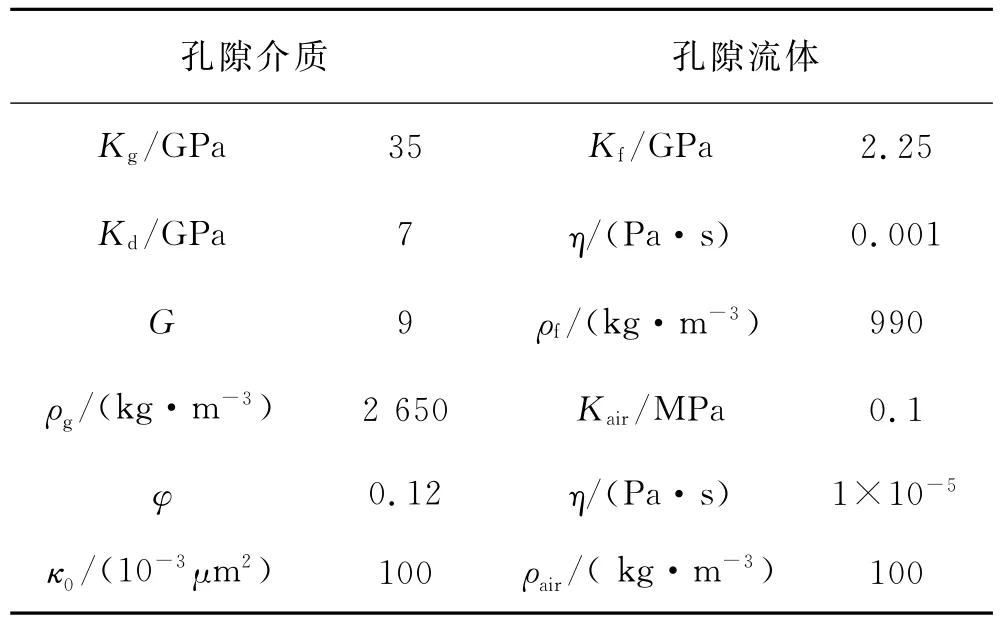
表2 MCRM模型和White模型参数[2-3]
图8为MCRM模型和White模型的速度频散曲线和衰减(1/Q)对比结果。由图8a可见,MCRM模型和White模型计算的频散曲线高、低频极限相同,且临界频率均在100Hz左右,但在从低频到高频极限的过渡区域,White模型的频散曲线更陡,MCRM模型的频散曲线有着更宽的频带过渡范围。衰减1/Q的计算结果表明,MCRM模型与White模型有着相同的衰减量级,但MCRM模型计算的衰减峰值要比White模型小(图8b)。引起上述现象的原因是White模型中孔隙流体均由统一大小的水包气球体构成,在临界频率处,衰减急剧发生;而MCRM模型中的包裹体有一定的分布范围,衰减的发生相对缓慢。图8显示,改进的随机孔隙介质模型中流体的分布更贴近真实岩石样品中孔隙流体的分布(图1)。
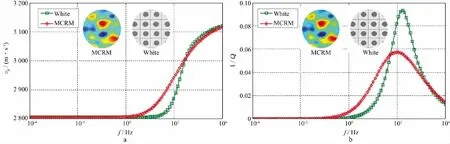
图8 MCRM模型和White模型速度频散曲线(a)和衰减1/Q(b)对比
由上述数值模拟分析可知,在储层流体具有中尺度斑块分布的情况下,在地震频带可能发生较强的频散和衰减现象。纵波速度在10~30Hz频带处于低频状态,在~104Hz频带处于高频状态,即纵波速度在地震频段和声学测井频段的弛豫状态可能不同。因此,在进行流体替换或对测井资料和地震资料进行对比分析时,必须考虑两者之间的差异。
2.3 储层参数对弹性波速度的影响
2.3.1 渗透率对弹性参数的影响
图9为利用MCRM模型计算的纵波速度和衰减随渗透率的变化情况。模型参数如表2所示,只将孔隙度φ改变为0.2。由图9可见渗透率降低并未影响纵波速度的高低频极限,且衰减峰值基本没有变化,但其特征频率随着渗透率的降低向低频方向移动,渗透率降低了2个数量级,特征频率减小,其变化范围基本涵盖了地震频段。这是因为流体流动机制引起的频散和衰减与流体可动性κ/η密切相关[30],减小岩石渗透率降低了流体的可动性,从而造成岩石相速度和衰减峰值向低频方向移动。即当地震波通过部分饱和岩石时,流体流动需要更长的时间达到平衡,这是典型的斑块饱和模型特征。传统的Biot理论特征频率为fc~η/κ,即随着渗透率降低,特征频率向高频方向移动。MCRM模型与Biot机制不同,随着渗透率降低,特征频率向低频方向移动,这与实际观测结果一致,体现的是两相流体斑块分布对地震波弹性性质的影响。
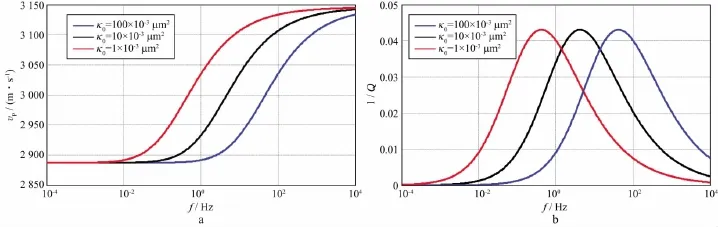
图9 纵波速度(a)和衰减(b)随渗透率的变化曲线
2.3.2 饱和度对弹性参数的影响
图10是利用MCRM模型计算的不同频率下纵波速度随含气饱和度的变化情况。完全饱水情况下,纵波速度最高,随着含气饱和度的增高,纵波速度降低,且降低程度与观测频率相关。不同频率下纵波速度随含气饱和度的变化范围在Gassmann-Wood(GW)和Gassmann-Hill(GH)模型的计算范围内,即弛豫与未弛豫的范围内。高频下(10 000Hz)纵波速度随含气饱和度近似线性降低,且向未弛豫的GH关系靠近;而较低频率(2Hz)下纵波速度随含气饱和度先降低到最大弛豫饱和度处,然后再增大,且变化曲线向弛豫的GW关系靠近。高、低频纵波速度随含气饱和度的变化规律存在差异。
地下气藏没有完全气饱和的情况,因为孔隙介质中总有一部分水附着在岩石颗粒表面,并且是不可动的;而水饱和情况常见,气藏的形成是一种天然气驱替地层水的过程,且总是部分饱和的,一般气藏的含气饱和度在微含气(Sg"10%)到几乎完全饱气(Sg# 95%)之间。基于数值模拟结果,地震频带(30Hz)纵波速度在含气饱和度10%~95%阶段变化范围为0.001%~2.300%,变化曲线相对平坦,这也是能够解释烃类检测具有极大挑战的原因。
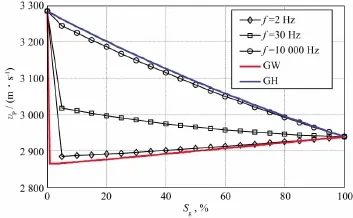
图10 不同频率下纵波速度随含气饱和度变化的情况
为了分析不同频段下纵波速度对含气饱和度的敏感性差异,分别对地震频带(30Hz)和测井频段(~104Hz)下不同含气饱和度的纵波速度和围岩饱水层纵波速度进行了对比,如图11所示。
基于数值模拟结果,在含气饱和度10%~75%段,地震频带下纵波的变化量均大于8%;在含气饱和度10%~40%段,测井纵波速度变化量较小,均小于5%,直到含气饱和度大于40%后变化量才大于5%。两者相比,气藏在地震频带的可探测性更强,但不幸的是,单独利用纵波速度参数判断气藏是否具有工业开采价值存在多解性。因此,在进行油气藏检测时需要利用多种敏感参数进行综合判断。
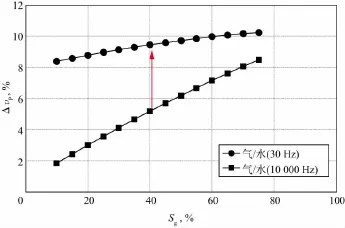
图11 不同频率下纵波速度对含气饱和度的敏感性分析
2.4 数值模拟结果与实验数据对比
图12为MCRM模型估计的衰减与实验数据对比。实验数据是Murphy利用共振棒技术测量一块高孔、高渗砂岩样品(φ=23%,κ=737×10-3μm2)得到的,岩石被空气/水两相饱和,含水饱和度约75%[31]。模型介质背景参数通过干岩石纵横波速度和密度计算得到。数值模拟结果表明,理论估计的衰减峰值与实验测量值在同一个数量级,但大于实验测量数据,其衰减特征频率略大于实验特征频率。出现这一现象一个可能的原因是实验测量数据受到样品边界效应的影响[31]。
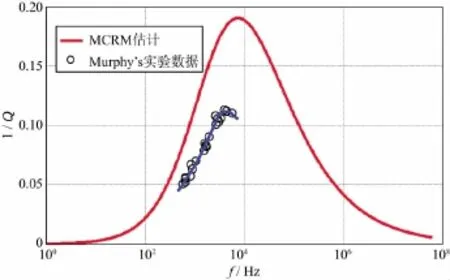
图12 MCRM模型估计的衰减与实验数据对比
此外,利用MCRM模型模拟了一块致密砂岩纵波速度随含水饱和度的变化情况,如图13所示。实验数据是Murphy利用共振棒技术测量一块致密砂岩样品(φ=8.5%)得到的,测量频率在5kHz左右[32]。在含水饱和度0~10%和90%~100%段,可能是由于岩石颗粒表面与流体间的毛细管作用、流体流动机制作用的影响[32],数值模拟结果与实验数据存在差异。在含水饱和度10%~90%段,MCRM模型能较好地模拟纵波速度随含水饱和度的变化情况。而地下气藏含水饱和度往往在5%~90%,因此,MCRM模型具有刻画地下致密储层纵波速度随含水饱和度变化的能力。
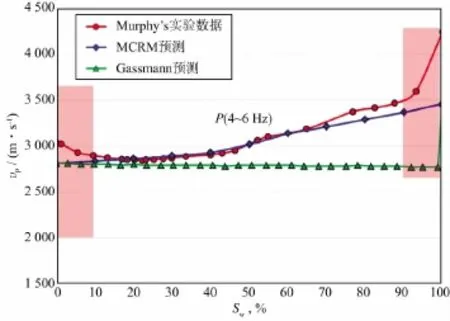
图13 MCRM模型估计的纵波速度随含水饱和度变化与实验数据对比
3 结束语
本文对随机斑块饱和孔隙介质模型(简称CRM)进行了研究并提出了改进模型(简称 MCRM)。MCRM模型改进了随机函数场的物理基础,并考虑了模型计算的有限性与理论假设无限性矛盾导致的计算误差。数值模拟结果表明,MCRM与CRM模型纵波速度的高低频极限相同,MCRM特征频率增大;两者衰减峰值相同,MCRM衰减曲线收窄;MCRM与White模型有相同的高、低频极限,但MCRM模型的频散曲线变化相对缓慢,衰减峰值稍小。
MCRM模型能够模拟渗透率、含水饱和度、频率等参数对速度频散和衰减的影响,并能在一定程度上解释实验室测量的高、低孔隙度砂岩频散和衰减数据。该研究成果可以更好地帮助理解岩石的黏弹性行为,提高定量地震解释的精度。
致谢:本研究基于作者博士论文部分章节,感谢中国石油大学(北京)油气资源与探测国家重点实验室提供的科研平台,感谢中石油勘探开发研究院地震岩石物理实验室提供的帮助。
[1] M LLER M T,GUREVICH B,LEBEDEV M.Seismic wave attenuation and dispersion resulting from waveinduced flow in porous rocks:a review[J].Geophysics,2010,75(5):75A147-75A164
[2] TOMS J,M LLER M T,CIZ R,et al.Comparative review of theoretical models for elastic wave attenuationand dispersion in partially saturated rocks[J].Soil Dynamics and Earthquake Engineering,2006,26(6/7):548-565
[3] TOMS J,M LLER M T,GUREVICH B.3Drandom patchy saturation model for velocity and attenuation in porous rocks[J].Expanded Abstracts of 75thAnnual Internat SEG Mtg,2005:1747-1750
[4] 侯波,陈小宏,李景叶.三相流体非均匀饱和多孔岩石声学模拟与分析[J].中国科学,2012,42(3):259-270
HOU B,CHEN X H,LI J Y.Acoustics simulation and analysis of three phase fluid patchy saturation porous rock[J].Scientia Sinica,2012,42(3):259-270
[5] 未晛,王尚旭,赵建国,等.含流体砂岩地震波频散实验研究[J].地球物理学报,2015,58(9):3380-3388
WEI X,WANG S X,ZHAO J G,et al.Laboratory study of velocity dispersion of seismic wave in fluidsaturated sandstones[J].Chinese Journal of Geophysics,2015,58(9):3380-3388
[6] 未晛,王尚旭,赵建国,等.致密砂岩纵、横波速度影响因素的实验研究[J].石油物探,2015,54(1):9-16
WEI X,WANG S X,ZHAO J G,et al.Laboratory investigation of influence factors on Vp and Vs in tight sandstone[J].Geophysical Prospecting for Petroleum,2015,54(1):9-16
[7] SMITHS C,TINNI A O.Microstructural controls on electric and acoustic properties in tight gas sandstones,some empirical data and observations[J].The Leading Edge,2010,29(12):1470-1474
[8] LEBEDEV M,TOMS-STEWART J,CLENNELL B,et al.Direct laboratory observation of patchy saturation and its effects on ultrasonic velocities[J].The Leading Edge,2009,28(1):24-27
[9] 邓继新,王尚旭,俞军.孔隙流体分布对部分饱和储层砂岩速度实验结果的影响及理论分析[J].石油物探,2005,44(5):495-498
DENG J X,WANG S X,YU J.The effects of pore fluid distribution to the experimental velocity of partially saturated reservoir sandstones[J].Geophysical Prospecting for Petroleum,2005,44(5):495-498
[10] 王大兴,辛可锋,李幼铭,等.地层条件下砂岩含水饱和度对波速及衰减影响的实验研究[J].地球物理学报,2006,49(3):908-914
WANG D X,XIN K F,LI Y M,et al.An experimental study of influence of water saturation on velocity and attenuation in sandstone under stratum conditions[J].Chinese Journal of Geophysics,2006,49(3):908-914
[11] 李晓波,董良国.斑状饱和介质的粘弹特征表征与地震波模拟[J].石油物探,2014,53(3):272-278
LI X B,DONG L G.Viscoelastic representation of patchy saturation media and its seismic wave simulation[J].Geophysical Prospecting for Petroleum,2014,53(3):272-278
[12] WHITE J E.Computed seismic speeds and attenuation in rocks with partial gas saturation[J].Geophysics,1975,40(2):224-232
[13] WHITE J E,MIHAILOVA N,LYAKHOVITSKY F M.Low-frequency seismic waves in fluid-saturated layered rocks[J].Journal of the Acoustical Society of A-merica,1975,57(S1):S30
[14] DUTTA N C,SERIFF A J.On White s model of attenuation in rocks with partial gas saturation[J].Geophysics,1979,44(11):1806-1812
[15] JOHNSON D L.Theory of frequency dependent acoustics in patchy-saturated porous media[J].Journal of the Acoustical Society of America,2001,110(2):682-694
[16] PRIDE S R,BERRYMAN J G.Linear dynamics of double porosity and dual-permeability materials.I.Governing equations and acoustic attenuation[J].Physical Review E,2003,68(3):036603
[17] PRIDE S R,BERRYMAN J G,HARRIS J M.Seismic attenuation due to wave-induced flow[J].Journal of Geophysical Research,2004,109(B1):B10201
[18] 巴晶,Carcione J M,曹宏,等.非饱和岩石中的纵波频散与衰减:双重孔隙介质波传播方程[J].地球物理学报,2012,55(1):219-231
BA J,CARCIONE J M,CAO H,et al.Velocity dispersion and attenuation of P waves in partially-saturated rocks:wave propagation equations in double-porosity medium[J].Chinese Journal of Geophysics,2012,55(1):219-231
[19] 刘炯,巴晶,马坚伟,等.随机孔隙介质中地震波衰减分析[J].中国科学,2010,40(7):858-868
LIU J,BA J,MA J W,et al.Analysis of seismic wave attenuation in random porous medium[J].Scientia Sinica,2010,40(7):858-868
[20] CADORET T,MARION D,ZINSZNER B.Influence of frequency and fluid distribution on elastic wave velocities in partially saturated limestones[J].Journal of Geophysical Research,1995,100(B6):9789-9803
[21] CADORET T,MAVKO G,ZINSZNER B.Fluid distribution effect on sonic attenuation in partially saturated limestones[J].Geophysics,1998,63(1):154-160
[22] KNIGHT R,DVORKIN J,NUR A.Acoustic signaturesof partial saturation[J].Geophysics,1998,63(1):132-138
[23] GUREVICH B,LOPATNIKOV S L.Velocity and attenuation of elastic waves in finely layered porous rocks[J].Geophysical Journal International,1995,121(3):933-947
[24] M LLER M T,GUREVICH B.One-dimensional random patchy saturation model for velocity and attenuation in porous rocks[J].Geophysics,2004,69(5):1166-1172
[25] M LLER M T,GUREVICH B.Wave-induced fluid flow in random porous media:attenuation and dispersion of elastic waves[J].Journal of the Acoustical Society of America,2005,117(5):2732-2741
[26] M LLER M T,GUREVICH B.A first-order statistical smoothing approximation for the coherent wave field in random porous media[J].Journal of the Acoustical Society of America,2005,117(4):1796-1805
[27] 郭乃川,王尚旭,董春辉,等.地震勘探中小尺度非均匀性的描述及长波长理论[J].地球物理学报,2012,55(7):2385-2401
GUO N C,WANG S X,DONG C Y,et al.Description of small scale inhomogeneities in seismic prospecting and long-wavelength theory[J].Chinese Journal of Geophysics,2012,55(7):2385-2401
[28] 徐振旺,安勇,支玲,等.运用分形方法模拟地震勘探中的三维随机介质[J].地球物理学进展,2014,29(3):1319-1325
XU Z W,AN Y,ZHI L,et al.Simulation of 3-D random medium in seismic propecting using fractal method[J].Progress in Geophysics,2014,29(3):1319-1325
[29] 杨帆.地震勘探中的三维随机介质模拟[J].石油化工应用,2016,35(2):72-77
YANG F Simulations and characteristics analysis of 3-D random medium in seismic prospecting[J].Petrochemical Industry Application,2016,35(2):72-77
[30] BATZLE M L,HAN D H,HOFMANN R.Fluid mobility and frequency-dependent seismic velocity:direct measurements[J].Geophysics,2006,71(1):N1-N9
[31] MURPHY III W F.Effects of partial water saturation on attenuation in Massilon sandstone and Vycor porous glass[J].Journal of the Acoustical Society of America,1982,71(6):1458-1468
[32] MURPHY III W F.Acoustic measures of patial gas saturation in tight sandstones[J].Journal of Geophysical Research,1984,89(B13):11549-11559
(编辑:戴春秋)
Study on the continuous random porosity model of patchy saturation
WEI Xian
(Research Institute of Petroleum Exploration and Development,PetroChina,Beijing100083,China)
To study the influence of patchy saturation on seismic wave propagation under mesoscopic scale,we investigate the continuous random model of patchy saturation,usually called CRM for short,and propose modified continuous random model(MCRM).Dispersion and attenuation characteristics of P-wave in inhomogeneous saturated porous media with gas and water are investigated by MCRM.Then,we compared the simulation results of three models with experimental ones and obtained the following conclusions.MCRM and CRM are provided with the same P-wave velocities at low or high frequency limits and the same attenuation peak,while the characteristic frequency of MCRM gets bigger and the attenuation curve of MCRM is narrowed.MCRM and White s model are also with the same P-wave velocities at low or high frequency limits,while dispersion curve of MCRM changes slowly,and attenuation peak of MCRM is slightly smaller.MCRM can simulate the effects of permeability,water saturation and frequency on the dispersion and attenuation and can explain the measured data of sandstone samples with high or low porosity.This study can help to better understand the viscoelastic behavior of rocks and improve the accuracy of quantitative seismic interpretation.
random patchy saturated,porous media,dispersion characteristic of compressional wave,statistical characteristics,sensitive parameter
P631
A
1000-1441(2017)03-0319-09
10.3969/j.issn.1000-1441.2017.03.002
未晛.随机斑块饱和孔隙介质模型研究[J].石油物探,2017,56(3):319-327
WEI Xian.Study on the continuous random porosity model of patchy saturation[J].Geophysical Prospecting for Petroleum,2017,56(3):319-327
2016-06-20;改回日期:2016-09-07。
未晛(1985—),男,博士,主要从事地震岩石物理、储层预测等研究。
国家重点基础研究发展计划(973计划)项目(2014CB239006)和国家科技重大专项课题(2016ZX05046-002)联合资助。
This research is financially supported by the National Key Basic R&D Program of China(973Program)(Grant No.2014CB239006)and the National Science and Technology Major Project of China(Grant No.2016ZX05046-002).

