基于高频金融数据下跳的检测

肖鸿民+李博亚

摘 要：文章基于近年來高频金融数据在跳的检测领域的研究成果，对预平均法下构造的检验统计量以及统计方法进行了介绍，并根据实验结果对预平均法的参数加以固定，使得统计方法更加具有可操作性，以此给出经过优化的金融数据中跳的检验方法，同时文章在最后通过数据模拟检测了这一方法的有效性。

关键词：高频数据；跳；预平均法

中图分类号：F224.13 文献标识码：A 文章编号：1671-2064（2017）09-0219-02

随着科技手段的进步，尤其是对计算机技术的发展，对海量的高频数据的收集和储存成本大幅下降，20世纪末以来高频数据在统计领域得以迅速发展，并且广泛应用到金融市场的实证研究中，极大地拓宽了金融工程等研究领域的方法和视野。

Black-Scholes（1973）期权定价模型提出后，对于资产价格的研究多假设价格服从连续路径，但是真实的市场行为中却常常出现一些极端事件，如政策调整引发的行业震荡、突发事件引起的恐慌情绪等都有可能会导致资产价格发生无法预料的大幅波动，这都体现出假设价格服从连续情况的局限性。 Merton（1976）提出在价格连续过程中引入不连续的跳过程来拟合价格，使得价格过程更加符合金融市场中存在的极端事件的发生，由此引发大量学者对跳的存在与否检测问题的研究热。

目前研究成果采取的资产价格过程是建立在连续时间上的随机微分方程：

其中是一个布朗运动过程，是一个局部有界的可料漂移过程，是波动率过程，则是跳过程。Ait-Sahalia and Jean Jacod（2009b）通过预平均法建立对跳的检验统计量，讨论了在不同噪声类型下该模型对跳的存在性的检测效果。

在本文着眼于金融序列中跳的存在性的检测问题上，在Ait-Sahalia and Jean Jacod（2009b）基于离散观测时间提出的预平均法（pre-averaging）的基础上，讨论了在参数的不同取值下所表现出对跳的检测能力的优劣，并通过固定参数给出更加特殊化和可操作性的检验统计结果。

1 预备知识

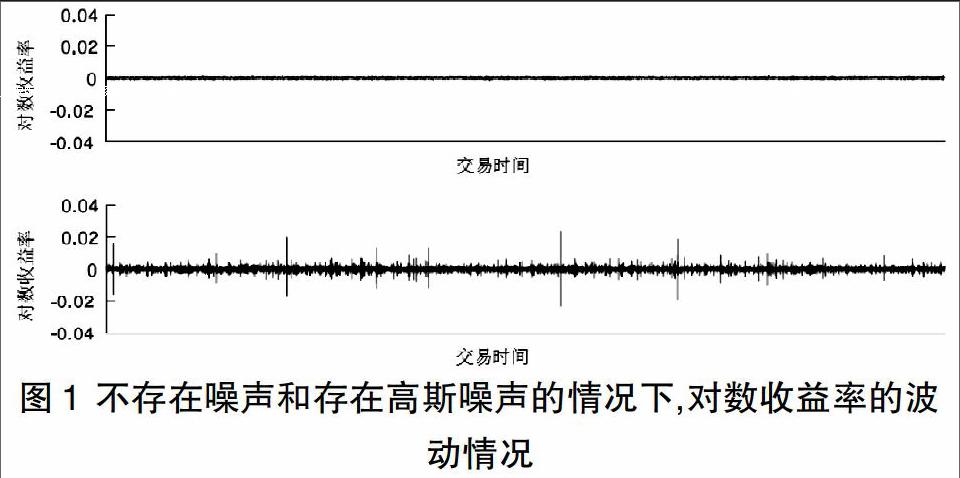
数据方面，本文选择沪深300指数（SH000300）作为研究样本，模拟中我们采取的观测时间长度为5天（），每天观测时长为4小时，并在取为时间间隔，选取区间为2016年4月25日到4月29日内的1200组数据。如图1所示。

贯穿整个模拟过程，我们固定，权重函数，，。特别地，在跳不存在时，统计量收敛于。我们令预平均法中选取的整数个数为，100或120，且，或6。

本文的不足之处在于，实证研究方面所采取数据的时间跨度较小，如果能够对更大时间跨度（比如一年的交易数据）进行实验，将会获得更好的检验结果。

5 结语

本文以预平均法为基础给出了高频金融数据下跳的检验统计量，在考虑高斯噪声的情况下，检验结果显示出对跳不存在这一原假设较为优良的检验结果。但模型就市场噪声类型的细分讨论上还有不足，距离实际应用仍旧存在差距，需要今后的研究中进一步对模型进行优化。

参考文献

[1]Jean Jacod.（2008）. Asymptotic properties of realized power variations and related functionals of semimartingales[J]. Stochastic Process. Appl. 118：517-559.

[2]Ait-Sahalia，Y. and Jean Jacod，Testing for jumps in a discretely observed process[J].The Annals of Statistic. 2009，Vol.37，No.1，184-222.

[3]Jean Jacod，Yingying Li，Per A. Mykland，Mark Podolskij，Mathias Vetterd， Microstructure noise in the continuous case： The pre-averaging approach. Stochastic Processes and their Applications[J].119（2009）2249-2276.

[4]Jacod， J.， Podolskij， M.， Vetter， M.， 2010. Limit theorems for moving averages of discretized processes plus noise[J]. Annals of Statistics 38：1478-1545.

[5]Jacod， J.， Li， Y.， Mykland， P.A.， Podolskij， M.， Vetter， M.， 2009. Microstructure noise in the continuous case： the pre-averaging approach. Stochastic Processes and Their Applications[J]：119， 2249-2276.