非水电解质溶液的状态方程
韩 正
北京 100029
非水电解质溶液的状态方程
韩 正*
北京 100029
以甲醇为溶剂的非水电解质溶液作为研究对象,构造出能够准确描述非水电解质溶液热力学性质的状态方程。本状态方程中包含两个可调节参数,在不改变可调节参数的情况下,该状态方程对于不同温度、摩尔浓度的非水电解质溶液的热力学性质保持着良好的预测能力。状态方程中的亥姆霍斯自由能由微扰理论计算得到,详细阐述非水电解质溶液的蒸汽压、溶剂活度的求解过程。
非水 电解质溶液 状态方程 热力学
根据电解质溶液中溶剂的不同,把以水作为溶剂的电解质溶液称作“水电解质溶液”,而把以其它物质(如甲醇、乙醇等)作为溶剂的电解质溶液称作“非水电解质溶液”。用来描述电解质溶液热力学性质的模型主要有两种:活度系数模型和状态方程模型,而本文论述的模型正是针对以甲醇为溶剂的非水电解质溶液所开发的状态方程模型。状态方程(Equation of State, EOS)是表征流体压强、密度和温度三个热力学参量的函数关系式,在确定了流体的状态方程之后,就可以确定流体在不同温度下的压强和密度值。电解质溶液的状态方程模型法是一种首先利用热力学理论确定电解质溶液体系的亥姆霍兹自由能,然后再将亥姆霍兹自由能与电解质溶液的其它热力学性质进行关联,如:活度系数、渗透系数、蒸汽压和密度等,从而在数值上对电解质溶液热力学性质进行准确描述的模型化处理方法。
电解质溶液在化学工业生产过程中十分常见,深入研究电解质溶液的热力学性质对于化工生产来说具有十分重要的意义。电解质溶液的蒸汽压预测工作在许多领域中扮演着非常重要的角色,这些领域包括:热泵吸附、精馏、有机溶剂循环利用和盐湖中贵金属的萃取等等。在过去的几十年里,电解质溶液热力学性质的测量和模型化处理已经在许多方面取得了很多成果,但是其中绝大多数的研究成果都是局限于水电解质溶液范围之内。到目前为止,非水电解质溶液的研究成果还是屈指可数。尽管对于水电解质溶液来说已经有很多实验数据存在于文献之中以供查阅,但是与之相较而言,可以查阅到的关于非水电解质溶液的实验数据还是少之又少。因此,开发出简单合理的预测性模型来描述非水电解质溶液的热力学性质对化工生产有非常大的指导意义。
1 理论基础
1.1 状态方程简介
本文研究对象是以碱金属卤化物为溶质、以甲醇为溶剂的非水电解质溶液。因为盐溶质是完全解离的,所以溶液中存在三种粒子:(盐)阳离子、(盐)阴离子和甲醇分子。盐离子被看成是带电的Lennard-Jones(LJ) 球体,它们身上具有可与甲醇分子形成氢键的缔合点,一个甲醇分子被看成是带有1个点偶极和3个缔合点的LJ球体。
在一定温度T和体积V条件下,电解质溶液系统由N个粒子组成,第i种物质的粒子数为Ni。运用微扰理论[1]可以将整个电解质溶液系统总的亥姆霍兹自由能A微扰展开成如下形式:
A=Ahs+ALJ+Aelect+Aassoc+Achain
(1)
其中:
Aelect=Acc+Acd+Add
(2)
式中,k为玻尔兹曼常数,上角标hs、LJ、elect、assoc、chain、cc、cd和dd分别代表来自硬球排斥、Lennard-Jones、静电、缔合、成链、离子-离子、离子-偶极和偶极-偶极作用的贡献项。公式(1)中Ahs、ALJ、Aassoc和Achain四项的表达式可以从文献2中查到,公式(2)中Acc、Acd和Add三项的表达式可以从文献3中查到。
利用计算机程序可以将上述各个亥姆霍兹自由能贡献项的数值计算出来,然后再将各个贡献项相加,最终确定电解质溶液系统总的亥姆霍兹自由能。
从压缩因子与密度和亥姆霍兹自由能的关系中可以得到电解质溶液系统的状态方程:
(3)
式中,ρ为粒子数密度。
组分k的化学位由下式得到:
(4)
将上述状态方程运用于非水电解质溶液,就可以计算出非水电解质溶液的蒸汽压、溶剂活度和密度值。
1.2 状态方程的计算功能
1.2.1 溶剂活度的计算
由活度的定义出发可以将溶液中的溶剂活度定义为:
as=fsxs
(5)
式中,下标s代表溶剂;as为溶剂活度;s为溶剂的活度系数;xs为溶剂的摩尔分数。
(6)
式中,下标0表示物质的纯态。
将上式带入式(5)即可得到电解质溶液溶剂活度的表达式:
(7)
1.2.2 蒸汽压的计算
(8)
将P=ρkT带入上式,可得:
(9)
由于溶剂是电解质溶液的主要组成部分,因此可以将溶剂的蒸汽压看做是电解质溶液的蒸汽压,由此可以得到电解质溶液蒸汽压的表达式:
(10)
2 状态方程的确立
本状态方程中包含可调节参数和不可调节参数。
2.1 不可调节参数的确定
不可调节参数主要包括甲醇溶剂的参数和盐溶质的阴阳离子参数。
2.1.1 甲醇溶剂的参数
本次研究所针对的非水电解质溶液的溶剂是甲醇。甲醇分子是一种带有1个点偶极和3个缔合点的LJ球体。通过本状态方程可以确定甲醇的偶极距为2.49D,甲醇的介电常数为32.49,这与298.15K下的实验值32.7非常接近。
对于甲醇来说,除了偶极距以外,在本状态方程中还有4个与温度无关的参数需要确定,这其中包括两个LJ参数(软球直径σ和能量参数ε/k)和两个缔合参数(缔合体积参数κassoc和缔合能量参数εassoc/k)。通过本状态方程可以确定这四个参数的数值,最终结果见表1。

表1 甲醇的状态方程参数和性质数据(298.15K、1bar)
在确定甲醇溶剂的四个参数的同时,本状态方程可以计算出甲醇的饱和液体在不同摩尔浓度下的密度和蒸汽压数值。该计算值与实验值吻合程度高,其温度范围:283.15K~333.15K,密度和压力的平均绝对偏差分别为0.043%和0.087%。计算所得的甲醇在298.15K时的密度为785.7344kg/m3,这与实验值786.24kg/m3非常接近。不同温度下甲醇的蒸汽压和密度分别见图1和图2(点代表实验值,线代表计算值)。

图1 不同温度下甲醇的蒸汽压

图2 不同温度下甲醇的密度
2.1.2 盐溶质的阴阳离子参数
每种盐溶质所包含的阴阳离子有2个LJ参数:离子直径σion和离子能量参数εion/k,其中离子直径σion可以从Pauling离子半径得到[6],离子能量参数εion/k可以通过Mavroyannis和Stephen离散理论计算得到[7]。
(11)
这里αion是从文献中得到的离子极化率[8];ne是离子中的电子数目——所有这些阴阳离子的参数见表2。粒子间所有的LJ相互作用都被考虑了进去,一共包括:甲醇-甲醇,甲醇-离子和离子-离子三种作用。
可以通过离子大小来预测每个离子上的缔合点数S,在通常情况下,离子越大缔合点数就越多。在本工作中,对于阳离子来说,Li+、Na+、K+的缔合点数都取7,Rb+取8,Cs+取10;对于阴离子来说,Cl-、Br-和I-的缔合点数分别取9、10和12。每个离子的缔合体积参数为κii=0.001。
2.2 可调节参数的确定
本状态方程包括两个可调节参数:一个参数是计算式(2)中Acd时所用到的有效平均离子直径σi,它对于所有种类的盐溶质来说都是可调节的;另一个参数就是对于每一种离子来说都不可忽略的离子-甲醇缔合能量参数εassoc/k,这个参数也可以通过本状态方程计算得到。本次忽略阴离子和甲醇的缔合作用,所以在本状态方程中不存在阴离子-甲醇缔合项,只存在两个参数。

表2 阴阳离子参数
注: ① 离子直径σion由鲍林离子半径得到。 ② 离子极化率αion取自文献8。 ③ εion/k由式(11)计算得到。 ④ S是EOS中需要用到的离子缔合点数。
本状态方程通过9种碱金属卤化物的甲醇电解质溶液的测试,溶液的共同状态是1bar、298.15K。计算所得溶液蒸汽压的平均绝对偏差(AAD)和可调节参数分别见表3,用来判断本状态方程的准确度。

表3 本状态方程的可调节参数以及计算所得的蒸汽压(P)和溶剂活度(a)的平均绝对偏差(AAD)(1bar、298.15K)

从表3中可见,本状态方程计算出来的非水电解质溶液的蒸汽压和溶剂活度的数值与实验值的吻合度很高,二者总的平均绝对偏差分别是1.112%和0.106%。因此可以判断:本状态方程能够准确地描述非水电解质溶液的热力学性质。
除了可以计算活度和蒸汽压之外,本状态方程还可以计算非水电解质溶液的密度,与活度系数模型相比这也是本状态方程的另一个优势功能所在。但是由于历史上对于非水电解质溶液的研究工作进行得太少,因此我们暂时还无法在历史文献中查询到相关的密度实验值作为本状态方程所计算出的密度计算值的参照物,所以在此就不再展示计算结果了。
2.3 可调节参数的通用性
本状态方程所包含的两个可调节参数具有很高的通用性:在不改变可调节参数的前提下,本状态方程针对同一种非水电解质溶液可以计算出它在不同温度和浓度下的蒸汽压和溶剂活度数值。举例来说,图3和图4展示本状态方程在使用表3中可调节参数的情况下计算出的相同非水电解质溶液在不同温度下的蒸汽压和溶剂活度数值——所用可调节参数是298.15K时的参数,计算出来的数值是更高温度状态下的数值。显而易见,此时本状态方程依然能够准确地描述非水电解质溶液的热力学性质,其平均绝对偏差见表4。
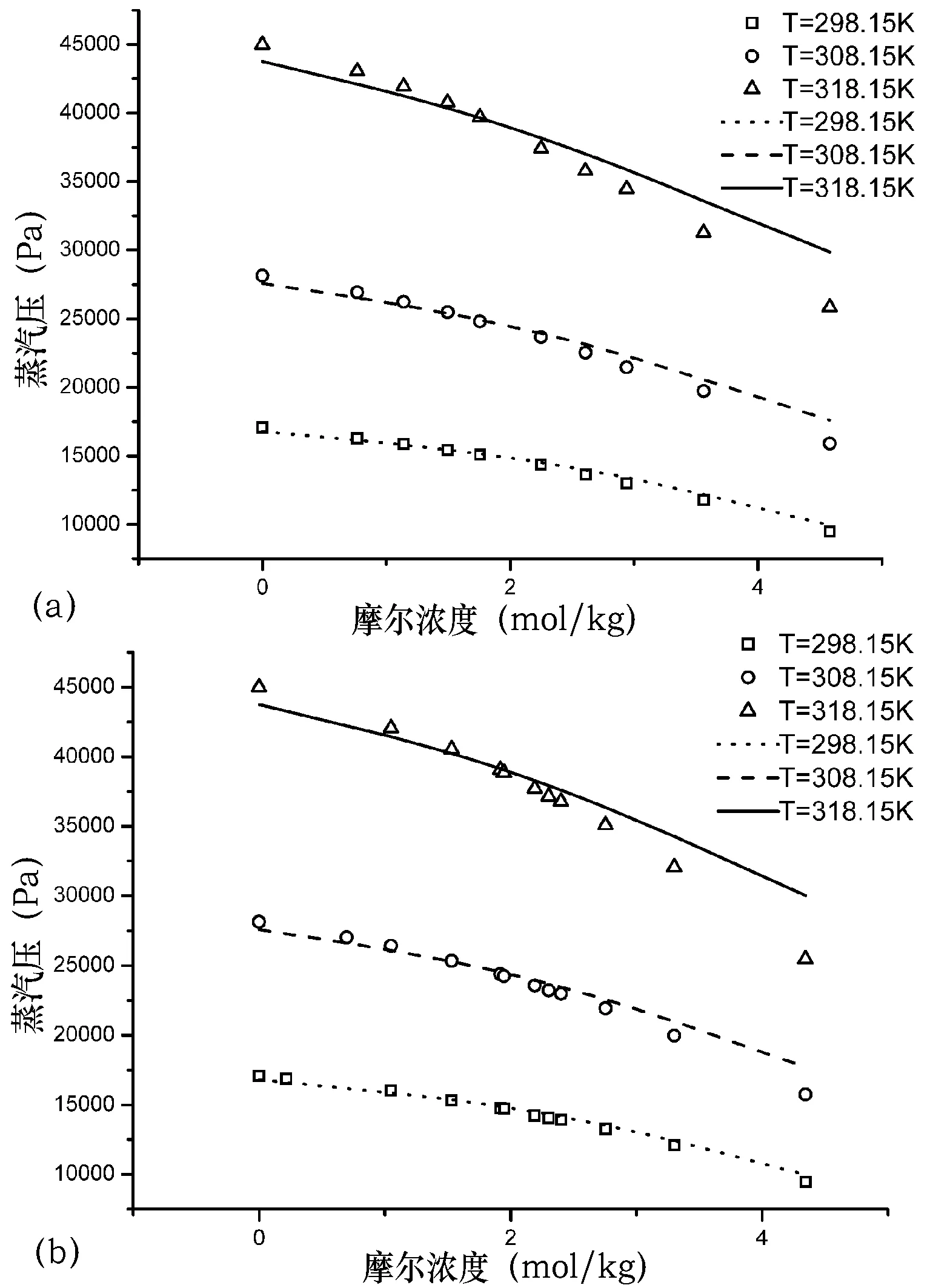
图3 甲醇电解质溶液的预测蒸汽压:(a)LiCl和(b)LiBr
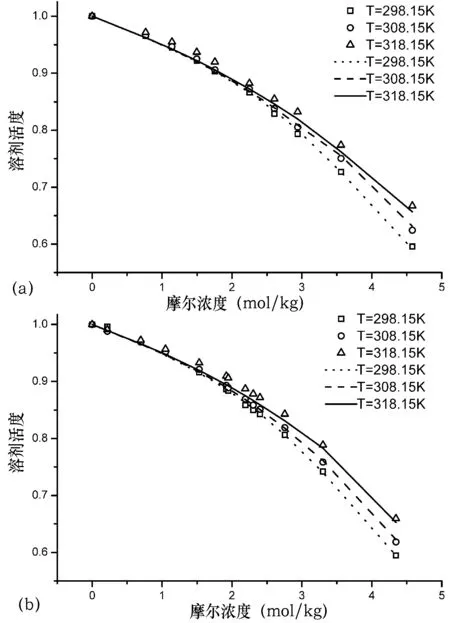
图4 甲醇电解质溶液的预测溶剂活度:(a)LiCl和(b)LiBr
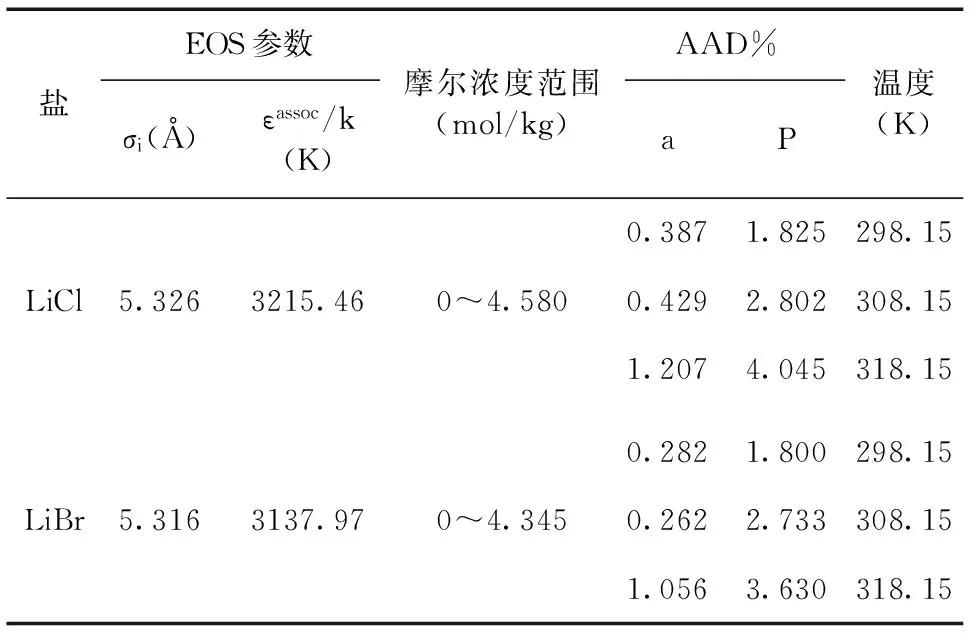
盐EOS参数σi(Å)εassoc/k(K)摩尔浓度范围(mol/kg)AAD%aP温度(K)LiCl5.3263215.460~4.5800.3871.825298.150.4292.802308.151.2074.045318.15LiBr5.3163137.970~4.3450.2821.800298.150.2622.733308.151.0563.630318.15
图3和图4中曲线是由本状态方程计算得到,点代表的是实验数据;状态方程所用的可调节参数同表3,平均绝对偏差参见表4。
值得注意的是,本状态方程的可调节参数的通用性还不仅仅局限于上述情况。在不改变可调节参数的情况下,把某种非水电解质溶液的摩尔浓度提高、甚至将摩尔浓度和溶液温度同时提高,本状态方程对于其溶液压力和溶剂活度的计算值相对于实验值而言依然保持着很高的吻合度。图5展示本状态方程使用表3中NaI—甲醇电解质溶液的可调节参数所计算出来的其在更高的摩尔浓度或者更高的温度和摩尔浓度下的溶剂活度和溶液蒸汽压数值曲线,平均绝对偏差见表4。可调节参数用的是0.024~0.755 mol/kg浓度下的参数,计算结果是0~4.338 mol/kg浓度下的结果。
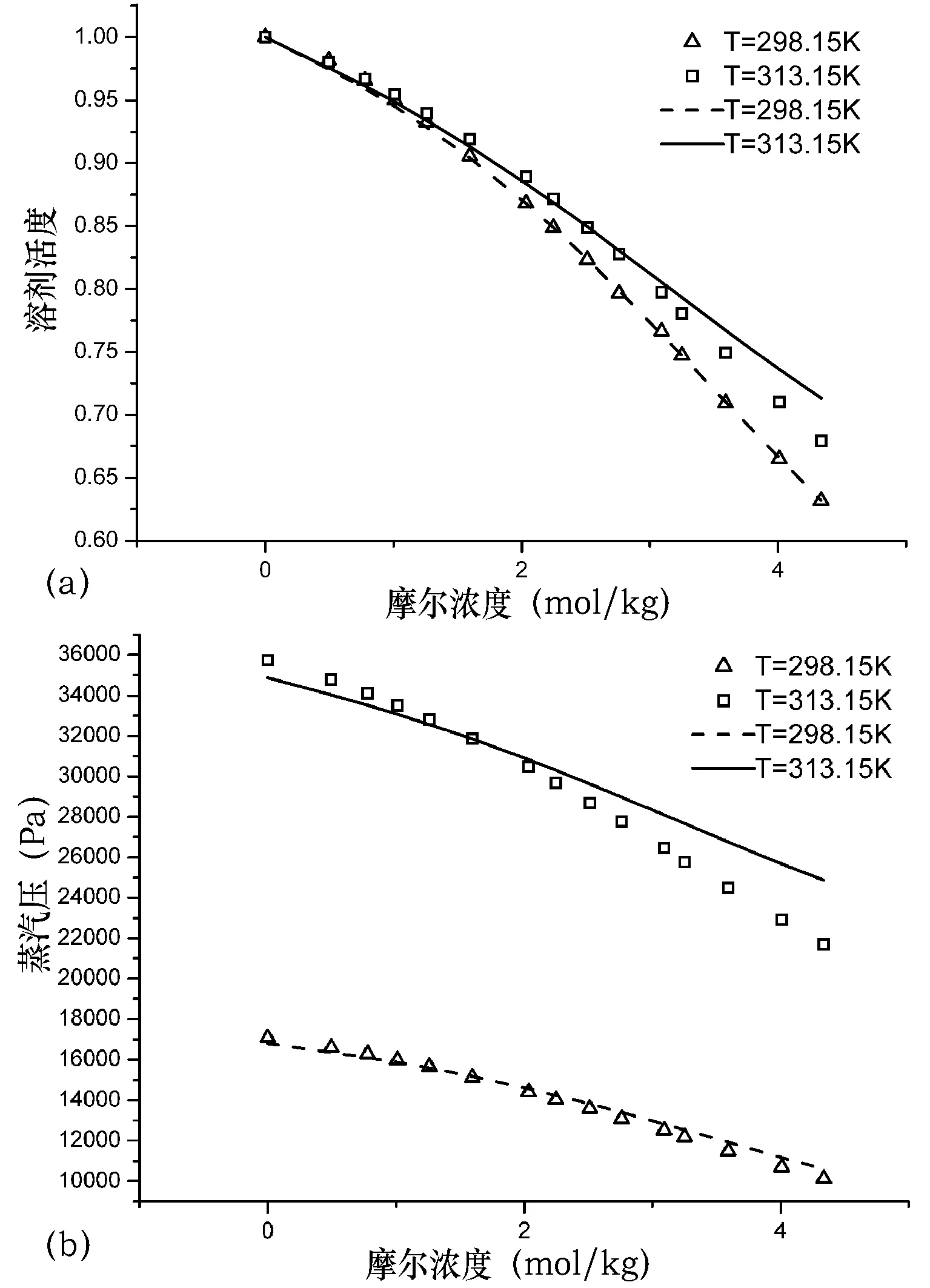
图5 高浓度下的NaI—甲醇电解质溶液的预测溶剂活度和蒸汽压
图5中曲线是由本状态方程计算出来,点代表实验数据;状态方程的所用可调节参数同表3,平均绝对偏差参见表5。

表5 不改变可调节参数,通过本状态方程计算出的蒸汽压(P)和溶剂活度(a)的平均绝对偏差(压力为1bar)
3 结语
目前关于电解质溶液的研究成果有很多,但大多数研究针对的对象都是以水为溶剂的水电解质溶液,而本状态方程所研究的对象是以甲醇为溶剂的非水电解质溶液。因此,本研究对于电解质溶液领域来说具有填补空白的意义。本状态方程包含了两个可调节参数,它能够准确地计算以甲醇为溶剂、以碱金属卤化物为溶质的非水电解质溶液的蒸汽压、密度和溶剂活度等热力学性质数据。该状态方程所包含的两个可调节参数具备很强的通用性——在不改变可调节参数的情况下,本状态方程对于不同温度、摩尔浓度的非水电解质溶液的热力学性质依然具备准确的预测性。
1 Boyle E J,Mcquarrie D A, Perturbation-theory of electrolyte-solutions [J], J Chem Phys, 1985, 83 (6): 3077-3082.
2 Liu Z P, Wang W C, Li Y G, An equation of state for electrolyte solutions by a combination of low-density expansion of non-primitive mean spherical approximation and statistical associating fluid theory [J], Fluid Phase Equilibria, 2005, 227 (2): 147-156.
3 Liu W B, Li Y G, Lu J F, A new equation of state for real aqueous ionic fluids based on electrolyte perturbation theory, mean spherical approximation and statistical associating fluid theory [J], Fluid Phase Equilibria, 1999, 158-160: 595-606.
4 韩 正, 非水电解质溶液系统的状态方程研究[D], 北京:北京化工大学, 2008:79-81.Han Z, The study about equation of state for nonaqueous electrolyte solution systems [D], Beijing: Beijing University of Chemical Technology, 2008: 79-81.
5 韩 正, 非水电解质溶液系统的状态方程研究[D], 北京:北京化工大学, 2008:82-83.Han Z, The study aboutequation of state for nonaqueous electrolyte solution systems [D], Beijing: Beijing University of Chemical Technology, 2008: 82-83.
6 Pauling L. The Nature of Chemical Bond, 3rd ed. Cornell University Press. Ithaca, NY, 1960.
7 Mavroyannis C, Stephen M J, Dispersion forces [J], Mol Phys, 1962, 5 (3): 629-638.
8 Coker H. Empirical free-ion polarizabilities of the alkali metal, alkaline earth metal, and halide ions [J]. The journal of physical chemistry. 1976, 80 (19): 2078-2084.
2017-01-23)
*韩 正:中国化工学会会员,中国化学会会员。2008年毕业于北京化工大学化学工程专业获硕士学位。E-mail:hzps2001@126.com。

