基于PFC-COMSOL联合开展软土固结细观机理研究

倪小东，尹学谦，蔡 钟

基于PFC-COMSOL联合开展软土固结细观机理研究

倪小东1,2，尹学谦1,2，蔡 钟1,2

（1. 河海大学 岩土力学与堤坝工程教育部重点实验室，江苏 南京 210098；2.河海大学 岩土工程研究所，江苏 南京 210098）

基于细观颗粒离散元方法建立土体细观结构性模型， 依据室内试验匹配模型细观参数， 采用COMSOL软件进行土体内部渗流场求解， 实现PFC-COMSOL联合开展软土固结研究， 最终将分析方案与室内固结试验数据进行对比。 研究结果表明： PFC使用聚粒模拟絮凝状软土 能较真实地 再现海相软土的细观结构特性；结构性蠕变对软土固结沉降量有一定影响，软土压缩量应考虑蠕变的影响；软土固结过程中 首先出现不均匀压缩， 超孔压完全消散后， 土体恢复均匀性。

软土固结；细观；PFC-COMSOL；蠕变

软土复杂的微观特性使其具有高孔隙率和低渗透性的特点，从而导致了软土压缩性高、固结缓慢的特性，因此从细观角度研究软土固结是有必要的。国内外众多学者基于不同的研究目的，分别采用不同的概化结构模型分析土体的细观结构[1-5]。但概化结构模型仅仅用于土体细观结构定性分析，为实现土体细观结构的量化研究，李向全等[6]根据土体具有的非线性特征，运用分形几何理论提出了粒度分维、颗粒定向分维等7项定量表征土体微结构状态的分维指标。随着扫描电镜、CT扫描仪的应用及计算机图像分析技术的发展，国内外学者在研究分析土体细观结构特性方面取得了丰富的成果[7-9]。众多学者已认识到土体固结过程中渗透系数及土体孔隙的变化，但目前对此规律的定量研究还比较少。

本文依托于前人的研究，从细观角度出发，开展软土细观结构特性研究，提出新的软土细观模型；开展软土的室内固结压缩试验，深入了解软土固结过程，试验结果作为选取模型参数的依据；根据软土的细观结构特征，利用基于离散元的颗粒流程序PFC2D建立符合软土细观结构特征的软土细观模型，采用测量圆监测土体孔隙变化，同时采用COMSOL软件建立土体内部的渗流场模型，实现PFC-COMSOL联合求解软土固结问题。

1 软土细观结构特征及细观模型的建立

1.1 软土细观结构特征

图1所示为各个地区通过电镜、X光线等扫描得到的软土微观图像[10-13]，各地软土颗粒细观形态虽有差异但以片状为主，而片状颗粒投影至平面近似为长条状，在建立软土细观模型时需体现该特点。

图1 不同地区软土的微观图像Fig.1 Microscopic images of soft soil in different regions

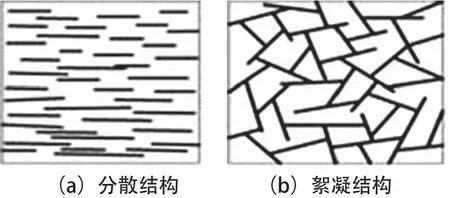
图2 粘土的两种基本结构Fig.2 Two basic structures of clay

图2 所示粘土的分散结构与絮凝结构均为粘土特有结构，分散结构土粒间表现为净斥力，絮凝结构颗粒间表现为净引力，土颗粒间的净斥力和净引力是产生这两种结构特征的根本原因。环渤海天津海岸带，珠三角海积软土区及长三角等地区广泛分布深厚软土，沿海软土细观结构可简化为图2所示絮凝结构，本文根据絮凝结构建立软土细观模型。固结前的软土颗粒通过颗粒搭接形成土体骨架，颗粒间的接触以面-边和面-角接触为主，而固结后这种结构遭到破坏，孔隙减小，颗粒间的接触转变为面-面接触。这种现象充分说明了在软土固结的过程中，土体骨架遭到破坏，土颗粒间的接触形式发生改变，相应的细观模型应能反映这种微结构变化过程。

1.2 软土细观模型建立

根据软土的细观结构特征，本文采用基于离散元的颗粒流程序PFC对软土材料模拟。采用PFC基本单元圆盘或球无法模拟满足软土细观结构特征的模型，但在PFC中可以通过FISH函数创建聚粒（CLUMP），可以将基本的圆盘或球形颗粒粘结在一起，形成各种形状的复杂颗粒，如图3（a）所示。聚粒（CLUMP）是具有固定空间关系的颗粒集合，无论受到多大的外力都不会发生破坏，聚粒内部颗粒间的相互作用也不用考虑。为了使软土细观模型能反映软土真实地细观结构特点，本文基于微观结构中平均方向角、定向角和平面形态系数三种结构定向性的定量评价指标，使用聚粒作为软土颗粒的絮凝结构细观模型，如图3（b）所示。

数值压缩试验还原室内压缩试验，示意如图4所示。初始状态时，模型底边长为6.18 cm，高2 cm，模型孔隙率为0.62，含有6 070个CLUMP单元，组成CLUMP的颗粒共有21 862个，其粒径为0.000 086 m，颗粒间的接触模型为接触黏结模型。

图3 软土细观模型Fig.3 Meso-model of soft soil

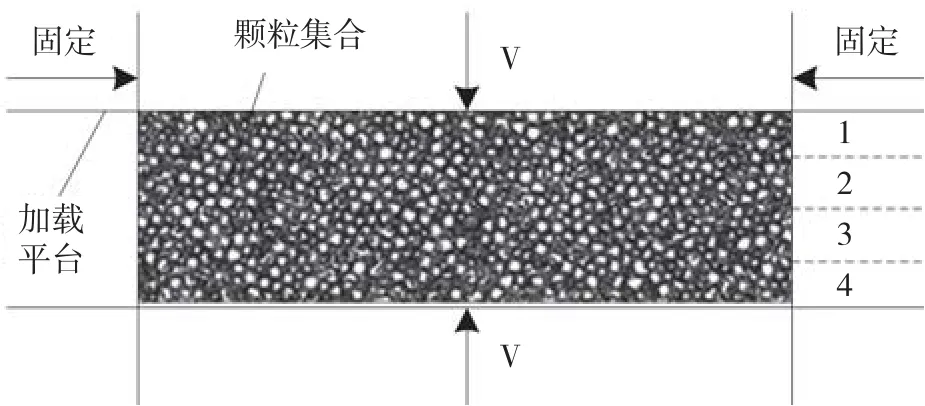
图4 数值压缩试验示意图Fig.4 Schematic diagram of numerical compression test

2 PFC-COMSOL联合求解方案

2.1 联合求解方案

根据固-液两相间的相互作用力计算方程[14-15]，将COMSOL中当前时步的渗流场转换为每一个颗粒受到的渗流力，导入PFC细观模型中，在渗流力与荷载的共同作用下计算至稳定状态，然后将PFC中模型的尺寸信息以及孔隙率变化情况导出，在COMSOL中建立对应尺寸的新模型，将新的孔隙率信息转换为新的渗透系数导入COMSOL中，开始下一轮计算。图5为联合求解数据交换示意图。

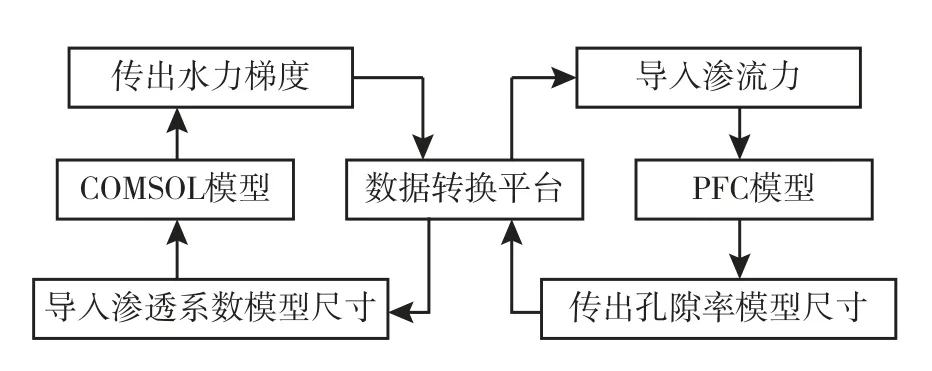
图5 数据交换示意图Fig.5 Data exchange diagram

在软土固结的过程中，随着孔隙率的减小以及土体内部结构的变化，土体的渗透系数也在不断变化，因此在固结过程中必须对土体的渗透系数不断修正。由于土体的固结压缩量并不是随着深度均匀发生的，靠近排水面的土层率先固结，因此在监测细观模型孔隙率变化情况时应选择不同的土层进行监测。

COMSOL软件模拟渗流场时渗透系数设定为常数，但是软土固结过程中，由于软土的结构调整以及孔隙率变化，材料的渗透系数变化较大，所以在固结过程中必须对软土材料的渗透系数进行修正。文献[16-17]给出了软土固结过程中渗透系数与孔隙比的关系式，本文通过此关系式修正渗透系数。

2.2 方案优势

软土固结的本质是土的压缩和水的排出，因此在模拟固结过程时，土体内部渗流场的模拟很重要。PFC虽然模拟颗粒流模型有着独特的优势，但其流场计算功能局限性较大，本文采用COMSOL软件对软土固结过程中的渗流场进行宏观模拟，能有效解决这一问题。

为得到固结过程中模型的孔隙比和渗透系数内部的变化规律，需要对模型的不同土层的孔隙比进行监测，PFC程序中可以利用测量圆有效实现这一功能，传统有限元软件建立的模型不能很好地反映固结过程中软土细观结构调整所引起的宏观参数（弹性模量、渗透系数等）的变化，从而导致模拟结果与实测数据相差较大。此外，测量圆可以监测固结过程中模型任意位置的应力应变及孔隙比，根据测量圆监测的信息，可以得到软土压缩过程e-p曲线，反推压缩系数，从而得到模型不同位置处压缩系数在固结过程中的变化规律。利用传统有限元软件建立的软土固结模型将软土假定为连续均质材料，无法反映软土的细观特点，因此对软土固结过程的模拟结果并不能令人满意，PFC程序可以使用CLUMP聚粒模拟软土絮凝状结构，可较真实地再现海相软土的细观结构特性，数值模拟结果更加准确。

3 室内试验及参数标定

3.1 室内固结试验

本文采用基于离散元的颗粒流程序PFC对软土材料模拟。PFC程序并不是直接给定材料的宏观力学参数，而是通过给定颗粒的细观参数来反映材料的宏观性质。利用PFC模拟软土材料的关键是建立颗粒细观参数与材料宏观参数对应关系。开展室内固结试验目的是提供参数标定需要的宏观参数，同时也用来对比数值模拟结果验证其合理性。

本文所用土样为取自浙江温州的滨海相饱和软土，其天然孔隙比为1.631s。使用三联式固结仪分级加压，加压梯度为1，每一级的荷载分别为：12.5、25、50、100、200 kPa 。图6为固结试验所得压缩量随时间的变化曲线，图7为压缩试验所得孔隙比随荷载的变化曲线（e-p曲线）。从图6中可以发现，在各级荷载作用下试样产生的压缩量主要发生在前100 min，100 min之后试样的压缩速率以及压缩总量均很小，说明前100 min土体内部的超孔压已经消散完毕，在这之后产生的压缩量是由于蠕变产生的。

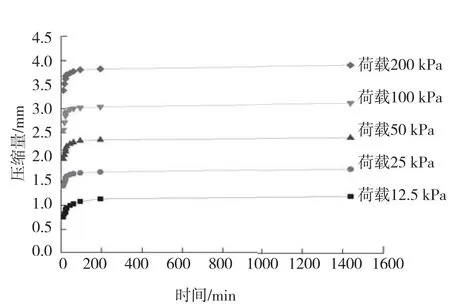
图6 压缩量随时间的变化曲线Fig.6 Curves of compression volume with time

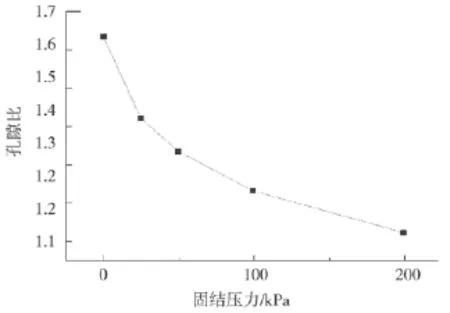
图7 孔隙比随荷载的变化曲线Fig.7 Curve of void ratio with load

由压缩试验得到的压缩量随时间变化的曲线，可以作为数值模拟试验结果是否合理的依据，试验结果与数值模拟压缩量与时间关系接近，则可以说明本文使用的方法是合理的。此外，由试验得到的软土宏观压缩特性是PFC参数标定的依据。

3.2 参数标定

软土细观模型中使用线性接触刚度模型、滑动模型以及接触黏结模型。颗粒接触模型确定之后，需要对各参数进行设置赋值，由于这些细观参数无法直接获取，必须通过建立颗粒细观参数与材料宏观参数对应关系得到，该过程称为参数标定。

软土固结问题，需要标定软土材料的压缩特性，在参数标定时建立颗粒细观参数与软土宏观压缩特性的对应关系。模拟过程采用PFC伺服机制在上下两个表面加压，分别计算模型在12.5、25、50、100以及200 kPa荷载下的压缩量，与前文压缩试验所得实际压缩量进行比较。当数值计算结果与试验结果相差较大时，调整颗粒的细观参数，重新模拟计算，直到模拟结果与试验结果基本一致时为止，此时颗粒的细观参数即为本次参数标定结果。

经过一系列参数调整，当颗粒细观参数为表1所示时，数值压缩试验结果与室内试验结果基本一致，如图8所示。

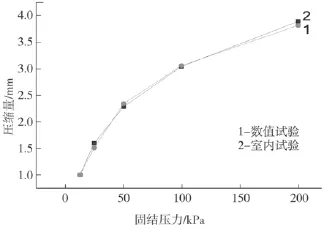
图8 压缩曲线Fig.8 Compression curve

4 数值试验分析

4.1 软土固结数值试验

利用上述联合求解方案对室内固结试验进行模拟，由于固结试验分级加载，此处仅展示第一级荷载（12.5 kPa）下软土的固结模拟过程。

数值试验模型详见图4，所用参数为上文参数标定所得，详见表1。PFC软件中测量圆可以对模型中任一位置变量进行监测，试验分析过程中将模型分成等厚度的四层，利用测量圆监测每层土样孔隙率随时间的变化情况。

在COMSOL达西定律模块中建立与PFC模型尺寸相同的渗流场模型，如图9所示，求解域具体设置见表2。

联合求解时步是指PFC模型与COMSOL模型每次交换数据的时间间隔，在固结试验前期，软土压缩的速度比较快，流场变化也很快，因此联合求解时步必须很小，而固结试验后期，软土压缩速度以及内部流场变化较慢，此阶段的联合求解时步可以适当增大。联合求解时步越小计算越精确，但由于软土固结是一个长时间的过程，时步太小会导致整个模拟过程计算量过大，因此必须选取合适的时步进行计算。分析模型时共进行11次交互运算，数据交换时刻分别为：30 s、1、2、4、10、20、36、64、100、200 min和24 h。

表1 PFC模型细观参数Tab.1 PFC model parameters

表2 求解域参数设置表Tab.2 Solution domain parameter table

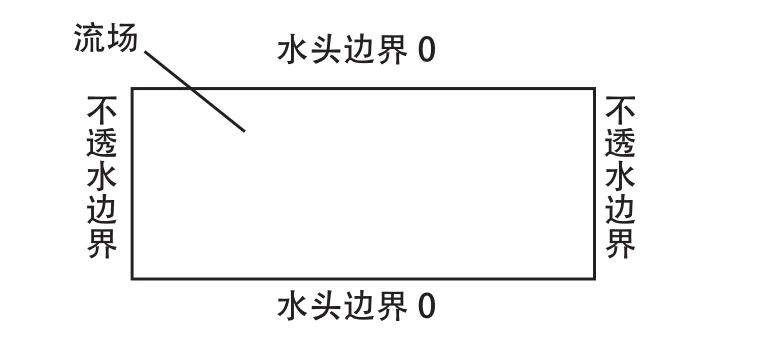
图 9 土体渗流场模型Fig.9 Model of soil seepage field

4.2 固结过程分析

模型建立后，进行联合求解，图10为t =4、64、100 min以及24 h时刻的PFC模型压缩图和COMSOL模型超孔压分布云图。

当t =4 min时，PFC模型产生了0.362 mm的压缩量，室内试验t =4 min时测得的压缩量为0.317 mm，误差为0.045 mm。此时的渗流场上下对称，上边界与下边界出的超孔压显著消散，中间的超孔压的消散程度远小于上下边界处。

当t =64 min时，PFC模型产生了0.929 mm的压缩量，室内试验t =64 min时测得的压缩量为0.837 mm，误差为0.092 mm。此时的渗流场依然上下对称，但超孔压的消散程度大大增加，中间的超孔压为1 260 Pa是整个区域内的最大值，仅为初始状态的十分之一。

当t =100 min时，PFC模型产生了0.991 mm的压缩量，室内试验t =100 min时测得的压缩量为0.887 mm，误差为0.104 mm。此时COMSOL模型中整个流场区域的超孔压已完全消散，模型固结度为100 %。

当t =24 h时，PFC模型产生了0.991 mm的压缩量，与t =100 min时模型产生的压缩量一致，说明在100 min到24 h这段时间内，PFC模型没有被压缩。室内试验t =24 h时测得的压缩量为1.00 2 mm，说明在100 min到24 h这段时间内，软土试样实际产生了0.115 mm的压缩量，模拟结果与试验数据存在一定的差异。

图10 P FC模型压缩与COMSOL模型孔压分布图Fig.10 Model compression and pore pressure distribution

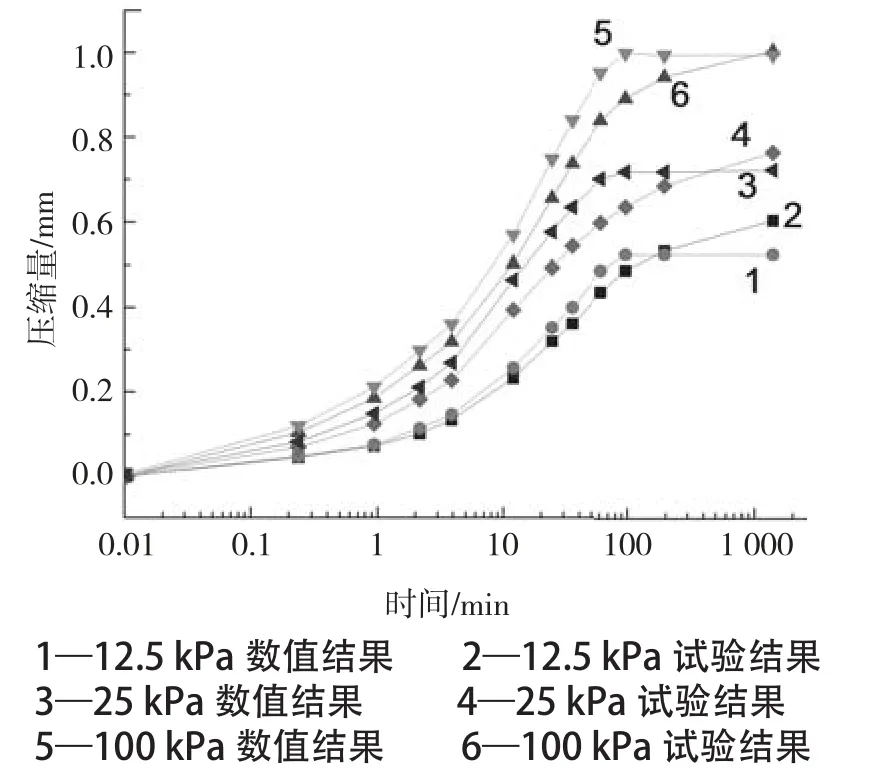
图1 1 压缩量随时间的变化曲线Fig.11 Curves of compression volume with time

图11 为室内固结试验软土试样压缩量随时间的变化曲线以及利用PFC-COMSOL联合求解方案模拟得到的模型压缩量随时间的变化曲线。从图中可以发现，前100 min数值模拟得到的软土压缩量不断增大，但100 min之后就不再变化，而试验测得压缩量始终都在增加。从64 min和100 min时的模型的孔压分布云图中可以看出，64 min时COMSOL模型中的超孔压尚未完全消散，而100 min时COMSOL模型中的超孔压已经完全消散，这一结果与固结试验的分析结论一致。本文的数值模拟的机理是根据COMSOL模型中渗流场的变化计算出颗粒受到的渗流力的变化，从而导致PFC模型的力学平衡破坏，产生新的变形直至进入新的平衡状态，一旦COMSOL模型中渗流场不再变化，PFC模型就不会产生变形，这也是数值模拟结果100 min之后压缩量不再变化的原因。而固结试验中软土试样在超孔压消散完毕后由于蠕变的作用将会继续变形，压缩量不断变大，只是压缩速度远小于超孔压消散之前的阶段。

根据标定得到的细观参数以及PFC-COMSOL联合求解方案模拟软土试样的固结过程，在12.5 kPa的荷载作用下模型的最终压缩量为0.991 mm而参数匹配时对应荷载下模型的压缩量为0.995 mm，误差很小，同时模拟得到的不同时刻模型的压缩量与试验结果差距也不大，说明了本文细观模型的参数标定结果以及联合求解方案是合理的。

软土固结过程中，蠕变始终存在，实际工程中软土地基往往有几米甚至几十米深，在荷载作用下软土地基内部超孔压的消散将是一个漫长的过程，这种情况下超孔压消散阶段的蠕变变形不能忽视。在分析工程实例中软土固结问题标定参数时适当考虑软土蠕变变形可以使模拟结果更加准确。

4.3 监控信息分析

在建立软土压缩细观模型时将模型分为等厚度的四层，随着模型的变形压缩，每一层土的厚度也发生变化。利用测量圆监控每一土层不同时刻的孔隙率变化情况，图12是荷载为12.5 kPa时各土层孔隙率随时间的变化曲线。从图中可以看出，土层1与土层4、土层2与土层3的孔隙率变化曲线基本一致，这是由于固结仪是双面排水，固结过程中土体的压缩量关于固结仪横向中轴线对称。土层1与土层4的孔隙率从固结开始就减小，而土层2与土层3在前1 min内孔隙率基本保持不变。从整个曲线的变化过程来看，土层2与土层3的孔隙率变化滞后于土层1与土层4，但最终四个土层的孔隙率基本一致，说明固结过程中首先出现不均匀压缩，即不同位置的土层压缩程度不一致。

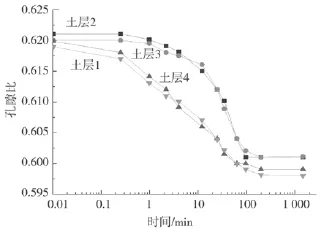
图1 2 孔隙率随时间的变化曲线Fig.12 Curves of porosity with time

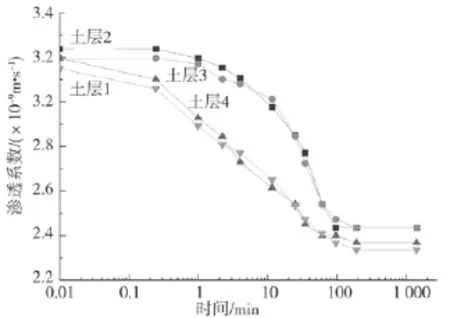
图1 3 渗透系数随时间的变化曲线Fig.13 Curves of permeability coefficient with time

根据PFC导出的不同土层的孔隙率n，转换为孔隙比e，根据文献[16-17]给出的公式可以计算不同土层不同时刻的渗透系数。图13是荷载为12.5 kPa时各土层渗透系数随时间的变化曲线，可以发现其变化趋势与孔隙率随时间变化的曲线几乎一致。初始时刻各土层的渗透系数接近，固结过程基本结束时各土层的渗透系数也接近，但土层2与土层3的渗透系数减小的进程明显滞后于土层1与土层4，这与各土层孔隙率的变化规律是一致的。

目前很多海边高速公路，大面积围垦等工程沉降计算方法假设整个沉降过程渗透系数不变，但是根据本文结论，软土的孔隙比，渗透系数在整个固结过程中是不断减小的，假设渗透系数不变计算出的结果是不准确的，本文得到的结论对软土地基处理具有一定的指导意义。

5 结论

1）采用CLUMP模拟絮凝状软土颗粒模拟软土压缩试验结果与室内试验结果吻合。

2）数值模拟过程中超孔压完全消散后，软土压缩量不再增加，而室内试验超孔压完全消散后压缩量在蠕变作用下继续增大。从压缩量与时间的关系曲线可以看出软土地基中软土蠕变作用不容忽视，软土地基处理工程中需重视软土蠕变作用。

3）软土固结过程中，土体首先出现不均匀压缩，渗透系数也出现不均匀变化，靠近排水边界处压缩量较大，渗透系数减小较快，远离排水边界压缩量较小，渗透系数减小较慢。

[1]彭涛，黄少康.吹填淤泥的工程地质特性研究[J].工程勘察，1999(5)：1-5.

[2]LAMBE T W. The structure of compacted clay[J]. Journal of Soil Mechanics and Foundation Division，ASCE，1958，84(SM2)：1-33.

[3]AYLMORE L A G. The structural status of clay systems[J]. Clays & Clay Minerals，1960，9(1)：104-130.

[4]OLPHEN H V. An introduction to clay colloid chemistry[M]. New York∶ Interscience Publishers，1963：1 59-192.

[5]SMART P. Soil structure，mechanical properties and electronmicroscopy[D]. Cambridge，England∶Cambridge University，1967.

[6]李向全，胡瑞林，张 莉. 软土固结过程中的微结构变化特征[J]. 地学前缘，2000，7(1)：147-152.

[7]王 清，肖树芳，王凤艳.土微观结构特征的定量研究及其在工程中的应用[J]. 成都理工学院学报，2001，28(2)：148-153.

[8]CETIN H. Soil-particle and pore orientations during consolidation of cohesive soils[J]. Engineering Geology，2004，73(Z1-2)：1-11.

[9]NAKAOKA K，YAMAMOTO S，HASEGAWA H，et al. Long-term consolidation mechanisms based on micro-macro behavior and in situ XRD measurement of basal spacing of clay minerals[J]. Applied Clay Science，2004，26(Z1-4)：521-533.

[10]王 婧. 珠海软土固结性质的宏微观试验及机理分析[D]. 广州：华南理工大学，2013.

[11]杨勇超. 宁波软土一维固结特性及微观机理研究[D].杭州：浙江大学，2014.

[12]CHENG X H，NGAN-TILLARD D J M，DEN HAAN E J. The causes of the high friction angle of Dutch organic soils[J]. Engineering geology，2007，93(1)：31-44.

[13]陈嘉鸥，叶 斌，郭素杰，等. 珠江三角洲软土 SEM微结构定量研究[J]. 电子显微学报，2001，20(1)：72-75.

[14]倪小东，王 媛，王 飞. 运用离散元法研究管涌机理[J].辽宁工程技术大学学报：自然科学版， 2010，29(2)：248-251.

[15]倪小东，王媛，陆宇光. 隧洞开挖过程中渗透破坏细观机制研究[J]. 岩石力学与工程学报，2010，29(Z2)：4194-4201.

[16]林 鹏，许镇鸿，徐 鹏，等. 软土压缩过程中固结系数的研究[J].岩土力学，2003，24(1)：106-108.

[17]胡孝彭. 固化淤泥持水与渗透特性试验研究[D]. 南京：河海大学，2013.

（责任编辑 王利君）

Study on the meso-mechanism of consolidation of soft soil based on PFC-COMSOL

NI Xiaodong1,2，YIN Xueqian1,2，CAI Zhong1,2
（1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering, Hohai University，Jiangsu Nanjing 210098 China；2. Geotechnical Research Institute , Hohai University, Jiangsu Nanjing 210098 China）

The mesostructure of soft soil has important influence on the consolidation process，it is of great guiding significance to consider soft soil structure from meso level and reveal the law of consolidation in a large area of reclamation project. In this paper, we establish the soil mesoscale model based on the discrete element method, match mesoscale parameters of the model according to the laboratory test, analyze the distribution of the seepage field in the soil body with COMSOL, realize to solve the consolidation problem of soft soil with PFC-COMSOL, and compare the analysis scheme with the laboratory test. Research results show that simulating flocculation soft soil with poly grain can truly react mesostructure characteristics of soft soil; Creep can influence the decrement in the process of consolidation of soft soil, creep should be considered in calculating the amount of soft soil compression; Uneven compression appears firstly in the process of consolidation of soft soil, after the excess pore pressure is dissipated completely, the soil recovers uniformity.

Soft soil consolidation; Mesoscale; PFC-COMSOL; Creep

TU41

A

1673-9469（2017）02-0030-07

10.3969/j.issn.1673-9469.2017.02.007

2017-01-08

中央高校基本科研业务费资助项目(2016B08114)

尹学谦（1992-），男，江苏宿迁人，硕士，主要从事岩土工程方面研究。