博弈论在社交网络中的应用
代翔
(中国西南电子技术研究所成都610036)
博弈论在社交网络中的应用
代翔
(中国西南电子技术研究所成都610036)
在线社交网络的迅速发展引起了各研究领域的广泛关注。经济学中,研究者们使用博弈论分析网络形成的机制,称为网络形成博弈,用于解释现有网络形成的原因。而在计算机领域,研究者们在社交网络的社团演化,链接预测,推荐系统等方面都提出了很多成熟的算法和模型,其主要是用于学习网络结构并对用户可能感兴趣的其他用户进行推荐。结合博弈论和链接预测,基于效用最大化理论指导链接预测问题的研究具有重要的意义。论文概述了博弈论在社交网络中进行链接预测,社团演化等方面的应用,并提出博弈论在网络演化方向的意义。
社交网络;博弈论;链接预测;网络演化
Class NumberTP311
1 引言
社交网络的发展正改变着我们的生活,它不断地缩短现实世界与网络世界之间的距离,满足了用户社交和获取网络信息的需求,用户可以通过社交网络发布信息、图片,进行交友等行为。根据相关统计,国内2015年11月份的社会化媒体排行榜如表1所示(JiaThis 2015)。以新浪微博为例,自2009年8月开始推出以来,用户数量一直在大规模增长,据微博数据相关统计显示,到2015年9月,微博月活跃用户达到2.22亿人,日活跃用户已达到1亿。可见社交网络用户基数庞大,网络拓扑结构复杂,因而其中蕴含的丰富信息引起了不同领域研究学者的广泛研究。
博弈论是经济学的一个分支,它研究人们的策略互动行为,并认为人人都会在约束条件下最大化自身的利益。经济学中有一个著名的研究方向,网络形成博弈(Network Formation Games,NFG),它研究社交网络的形成机制。在网络形成博弈模型中,每个结点拥有一个收益函数来表征通过当前网络拓扑结构,该结点所做的某项决定或与其他结点建立的某条链接给自身带来的收益[1]。在社交网络中,用户结点之间存在复杂的链接关系,每个用户结点在与其他用户建立链接关系时都希望最大化自身的收益。对于社交群体,都会存在一个稳定状态,即当前群体中的每一个结点的收益都处于最大化[5]。
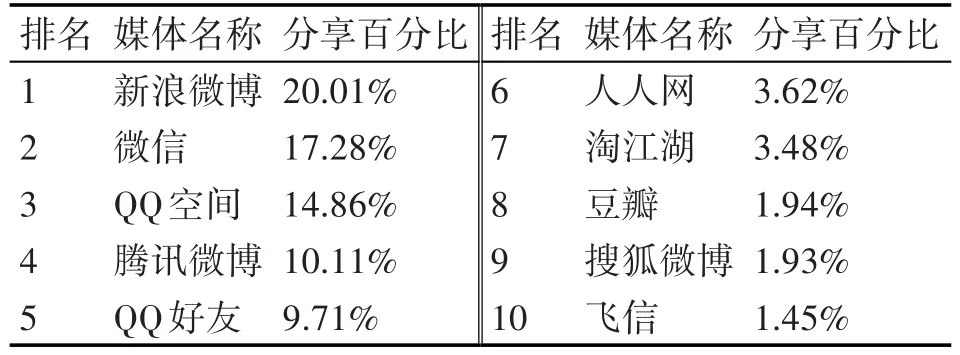
表12015 年11月社会化媒体排行榜
针对在线社交网络衍生出的研究方向十分广泛,比如链接预测、推荐系统、社团演化等,各种模型和算法层出不穷,近年来,有研究提出在传统方法的基础上结合博弈论的思想来提高链接预测和社团演化分析的准确性。
随着社交网络的飞速发展,大量的用户交互数据随之而来,而整个网络也时刻都在动态演变,如何有效地分析用户行为之间的相互影响以及网络的演化过程成为一个新的研究热点。而真实世界的网络普遍具有小世界特性,这种特性最早可以追溯到社会学家Milgram在1967年所做的社会学实验,发现了“六度分离(six degrees of separation)”现象[9]。这种现象表明社会关系网络中人与人之间的距离是很短的。1998年Watts和Strogatz[10~11]首次提出了小世界模型,揭示了小世界特性形成的原因。由于社会网络都具有很强的小世界属性,因此在小世界网络上研究群体博弈行为将更加具有现实意义,因此本文将重点关注博弈论在链接预测和社团演化等方面的应用。
本文主要介绍博弈论在社交网络中链接预测方面的应用,并提出运用博弈论进行网络演化分析的思路。
2 相关背景
博弈论:博弈论亦名“对策论”、“赛局理论”,属应用数学的一个分支,主要研究公式化了的激励结构间的相互作用。它是研究决策主体的行为发生直接相互作用时候如何决策以及决策的均衡问题,是具有斗争或竞争性质现象的数学理论和方法,也是运筹学的一个重要学科。博弈论考虑游戏中的个体的预测行为和实际行为,并研究它们的优化策略。
·纳什平衡:所谓纳什均衡,是指一种策略组合,在该策略组合上,任何参与人单独改变策略都不会得到好处。即如果在一个策略组合上,当其他人都不改变策略时,没有人会改变自己的策略,则该策略组合就是一个纳什均衡。社交网络中的纳什平衡,我们可以直观地理解为:在当前网络中,没有任何一个用户可以通过单方面的改变自身的链接而获得更高的收益[6]。也就是说,在当前网络结构中,所有用户结点的收益都达到最大时,则当前网络处于纳什平衡状态。
·异构信息网络:如果一个网络包含多种类型的结点和链接,那么该网络为异构信息网络。异构社交网络可用G=(V,E)来表示,其中V是一个不同类型结点集合的并集,E是一个异构链接集合的并集。社交网络就是一个典型的异构信息网络。
·小世界网络:小世界网络是一种图的类型,图中大部分结点不与彼此邻接,但大部分结点可以从任一其他点经少数几步就可到达。若将一个小世界网络中的点代表一个人,而点之间的连线代表人与人认识,则这小世界网络可以反映陌生人由彼此共同认识的人而连结的小世界现象[4]。
·网络形成博弈(NFG):NFG通常用来分析用户在社交网络中建立链接时的判断力,它最核心的部分是效益函数,该函数可以解释当前特定网络的形成原因。不同的效益函数构成了不同的网络形成博弈模型,也就使得用户通过彼此之间的链接可以建立不同的网络结构。而网络形成博弈的目的就是通过效益函数分析网络在达到纳什平衡的过程中,其中用户所获得的效益。
3 链接预测中的博弈论
3.1 链接预测与博弈论
链接预测是社交网络研究的热门方向之一。如图1,它描述了6个社会网络用户之间的朋友关系(链接)。实线表示时刻已经存在的朋友关系,虚线表示在区间之间形成的新朋友关系(新链接)。例如时刻,Dave和Bob是朋友,Dave和Cindy不是朋友。但是到了时刻,Dave和Cindy已经成为了朋友,Eric和Alice也成为了朋友。
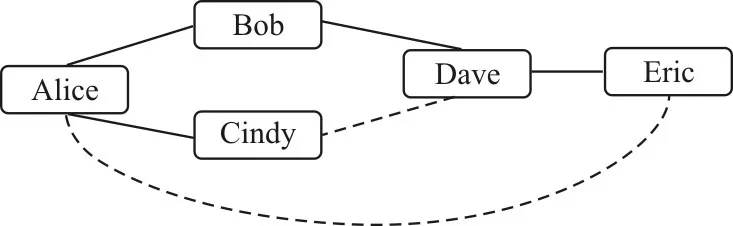
图1 社交网络中的链接预测
传统的链接预测方法认为任意用户之间都可能形成新链接,即在所有时刻未链接的用户都可能在时刻形成链接。它的做法是:计算所有在时刻未链接用户之间的相似性,认为相似性排名前k的用户对在时刻会形成链接。
传统链接预测的研究者们提出了很多优秀的方法和模型,文献[14]利用社交网络的拓扑特征来预测用户间的可信及不可信关系;文献[12]提出通过捕获信任的演化进行链接预测的模型;在文献[13]中作者设计因子图方法针对跨异构网络的用户进行链接预测等等。
然而上述模型和算法几乎都基于相似性分析或传播分析,均没有考虑用户的收益变化,显然这种做法是不合理的,社交网络的用户会自由选择与哪些用户形成链接,他们会考虑与其他用户形成链接是否会为自己带来收益的一系列问题。
在链接预测中引入博弈论的思想,就可以很恰当地解决这一系列问题。基于博弈论的思想,用户会有“条件”地进行选择,他们都是为了自身利益最大化,选择与某些用户形成链接,而拒绝与其他用户形成链接。比如在图1中,Dave在时刻只与Cindy形成链接,而没有与Alice形成链接。
在基于博弈论解决链接预测的方法中,网络形成博弈(NFG)与机器学习模型结合的方式[2],是目前提高链接预测准确度很有效的方法,其中很重要的一种模型是BPRLGT模型。
3.2 BPRLGT模型
文献[2]提出了两个利用网络形成博弈提高链接预测准确度的方法:其一,直接将博弈论结合到机器学习模型中;其二,将网络形成博弈模型结合到贝叶斯排序框架中进行链接预测。两种方法的核心思想都是在现有的链接预测模型基础上,考虑用户自身收益的变化。
现有的链接预测模型及算法基本都基于相似性分析或者传播分析,并以最大化预测准确度为目标。而网络形成博弈是在当前网络中,没有用户可以通过建立新的链接来提高自身收益的假设下,以最大化用户收益为目标。因此在对两个模型进行结合时,存在以下三个问题:第一,大多数网络形成博弈模型基于没有用户可以通过建立新的链接来提高自身收益的假设,分析现有网络的形成,这个假设与链接预测冲突;第二,网络形成博弈分析的目标与链接预测目标不一致;第三,目前没有在训练模型时考虑用户收益的链接预测模型。
为了解决上述三个问题,文献[2]提出了以下解决方案,如图2所示。
首先计算原始网络中各用户结点的收益;然后使用机器学习算法生成为原始网络推荐的链接;最后计算加入推荐链接后的网络中各用户结点的收益。比较初始网络G与加入新链接后的网络G+{eij}中各结点的收益变化,对机器学习算法生成的推荐链接进行重新排序,则得到最终的推荐链接列表。例如,对于用户i,通过计算得到加入新链接后该用户的收益变化为


图2 算法流程图
若Δi≥0,则eij是对用户i有益的链接;若Δi≥0且Δj≥0,则eij为用户i和用户j之间的互惠链接。计算收益变化后,保留有益链接,惩罚推荐链接集合中虽排名在前但无法提高用户收益的链接。通过这样的方式达到向用户推荐既是由链接预测模型推荐又可提高用户收益链接的目的,从而提高了链接预测的准确度。
上述方法将网络形成博弈结合到机器学习模型中,但两者是互相独立的,即在训练机器学习模型时并未考虑网络形成博弈,在机器学习模型进行链接预测时也并未考虑用户收益问题。为了使两者更好的结合,作者[2]将网络形成博弈模型与贝叶斯排序模型结合,提出了使用博弈论进行链接预测的贝叶斯个性化排序模型(Bayesian Personalized Ranking for Link recommendation with Game Theory,BPRLGT)。BPRLGT模型以贝叶斯个性化排序框架为基础,使用博弈理论进行抽样,将生成的训练数据用于模型训练,并考虑网络拓扑的影响。该模型基于用户更倾向于与朋友的朋友建立连接的假设,使用随机梯度下降算法进行学习。该模型选取样本的流程如图3所示。

图3 BPRLGT样本选取流程图
如图3所示BPRLGT采用博弈论的思想进行样本数据选取的核心为如果用户j通过相似性计算推荐给u的概率很高,但是增加链接euj未提高u的收益,则通过最大化puk(u与k建立链接的概率)和puj(u与j建立链接的概率)的方式对j进行惩罚。
在模型的学习过程中,BPRLGT不仅实现了观测链接优先顺序的最大似然,而且考虑了每个用户的收益。
为了验证BPRLGT模型的有效性,文献[2]中作者使用Ciao,Epinions,COL和Facebook四个数据集,对现有的链接预测方法与结合BPRLGT的链接预测方法进行了比较。结果表明,在多个度量标准中,结合BPRLGT模型的链接预测方法比现有的链接预测方法的准确度高。同时,与BPRLGT相比,结合BPR模型的链接预测方法在部分数据集上效果较差,原因是BPR在训练数据的选取时采用的是均值采样,并未考虑网络的拓扑结构。
3.3 小结
文献[2]结合博弈论的思想进行链接预测,为我们提供了一个新的研究方向。无论是链接预测还是好友推荐,或是异构信息网络中的推荐应用,都可以加入博弈论的思想进行分析。
网络形成博弈通常用来分析用户在社交网络中建立链接时的判断力,其最核心的部分是效益函数,该函数可以解释当前网络的形成原因。不同的效益函数构成了不同的网络形成博弈模型,也就使得用户通过彼此之间的链接可以建立不同的网络结构。而网络形成博弈的目的就是通过效益函数分析网络在达到纳什平衡的过程中,其中用户所获得的效益。首先,结合网络形成博弈,可以提出不同的收益函数分析结点收益的变化情况。通过各结点的收益变化情况,我们可以进一步对社交网络结构的变化进行分析。除此之外,结合上下文语义与网络形成模型来进行链接预测也是一个很有意义的研究方向。再进一步,将博弈论与其它机器学习模型,如马尔科夫决策过程,融合也是未来一个有意义的研究点。
4 社团演化中的博弈论
4.1 社团演化
社交网络是一种典型的复杂网络。复杂网络是这样定义的:具有自组织、自相似、吸引子、小世界、无标度中部分或全部性质的网络称之为复杂网络。复杂网络是一种呈现高度复杂性的网络,其特点主要有:
小世界特性:小世界特性被称之为六度空间理论或者是六度分割理论,小世界特性指出:社交网络中任何一个成员和任何一个陌生人之间所间隔的人不会超过六个。
无标度特性:现实世界的大部分网络都不是随机网络,极少数的节点往往拥有大量的连接,大部分的节点连接数都比较稀少,节点度数符合幂律分布。节点度分布符合幂律分布的复杂网络称之为无标度网络。
社团结构特性:社团结构是指整个网络是由若干个“群(Group)”或“团(Cluster)”构成的。例如社会网络中的朋友圈,其中每个成员都认识其他成员。每个群的内部节点之间的连接相对比较紧密,但是各个群之间的连接却比较稀疏[8]。
其中网络社团结构的演化性是社交网络的一个重要特性。用户(网络节点)的兴趣、角色、社会地位等因素随时间不断地变化引起网络结构隐式地变化。与此同时,社团结构的改变也反过来影响着用户的兴趣、角色、社会地位。
社团演化问题的研究由来已久,目前主流的研究方法分为两类:独立聚类和演化聚类。独立聚类是对动态网络按时间取一系列网络状态,每个网络状态就是该时刻网络的一个快照,然后将社团发现算法分别应用于每个网络快照。比较不同时刻的社团,便可以定义并发现社团增长、收缩、合并、分裂、产生和消失等社团演化事件[7]。演化聚类方法通过考虑网络演化的时间信息,确保社团结构在连续时间戳上的平滑性,该方法可以克服社团发现算法或网络噪声带来的随机性问题[15~23]。
4.2 经典博弈论与演化博弈论
经典博弈论基于两个假设:一是参与者完全理性,即参与者对自己和对手的策略以及不同策略组合下的收益函数都有明确的认知;二是参与者有共同的共识,所有的参与者都知道其他参与者是完全理性的。在这两个假设下参与者会追求自身利益的最大化。典型的例子就是囚徒困境博弈。
演化博弈论是基于现实社会中,个体不可能是完全理性的(有限理性)这个前提,它认为个体通过不断吸取经验来调整自己的策略以适应环境。演化博弈论是经典博弈论由完全理性转向有限理性的进化过程中产生的一种研究手段,放宽了经典博弈论中完全理性假设的限制,参与博弈的对象不再是确定的。而且博弈的过程不再是经典博弈论中的一次博弈,而是会发生多次,即动态演化,这也为经典博弈论中出现多个纳什均衡点而无法收敛的情况提供了一种更有效的方法[24]。
4.3 社团演化与博弈论
社团演化是社交网络研究的传统方向,针对这个问题的研究已趋于成熟,但从博弈论的角度,分析用户在社团演化过程中所获利益变化情况的研究还较少。在社团演化领域中融入演化博弈论,思路是将网络中的节点认为是博弈的参与者,节点之间的边看作是参与者之间的关系,博弈发生在有边的参与者(节点)之间。网络演化的过程是:首先,节点随机选择邻居节点进行博弈并获得收益;其次,节点会根据收益值进行博弈学习,同时调整网络结构。不断执行这两个过程,直至达到平衡状态。演化博弈主要涉及三个要素:网络模型,博弈模型和策略更新规则。
一般的网络博弈研究中,网络结构是静态不变的。近年来,人们逐步关注在演化博弈论的影响下,网络结构是如何发生变化的。Zimmermann等提出了一个动态网络囚徒困境博弈模型[25];Li等提出了一种由演化博弈驱动生成的无标度网络型[26];Helbing等提出成功驱动的博弈模型[27]。
文献[3]提出了在异构信息网络中利用博弈论进行社团演化聚类的框架:GHIN,该框架将异构信息网络中结点的不同类型作为博弈论中的一个玩家,将每一个聚类结果作为一个纳什平衡点。经过实验证明,该框架的聚类效果比一些著名的聚类算法都要好,该框架的特点是聚类结果依赖于当前网络结构的回报函数。其算法流程如图4所示。

图4 GHIN算法流程图
4.4 小结
结合博弈论进行社团演化分析,使得演化的发生可以有效地解释。我们认为网络的演化本质上是结点间边的变化,而边的变化必定影响结点的收益,同时假设社交网络中的点都是有限理性的,每个点都以自身利益最大化为目标,基于上述两点,首先要定义衡量结点收益及社团收益的权值函数,以此作为收益,并以网络趋向于利益最大化的方向发展为基本假设,分析网络中链接的变化过程,直至网络到达纳什平衡状态。主要思路如图5所示。
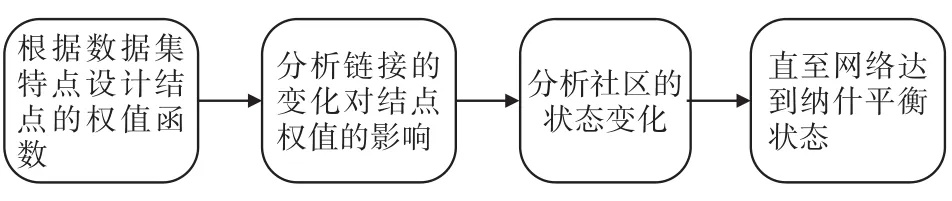
图5 分析流程图
5 结语
博弈论所研究的是理性的决策者之间冲突及合作的理论,可以为实际决策提供理论基础和方向指导。其最终追求结果是使博弈方达到利益最大化的均衡。在生活中,博弈仍然无处不在。博弈论代表着一种全新的分析方法和全新的思想,而我们所在的现实及网络世界,利益分析无处不在,结合博弈论进行社交网络分析是一个合理并新颖的思路。
本文概述了博弈论在链接预测,聚类等方向的应用。在社交网络中博弈论运用的核心为,将用户在社交网络中的行为看做博弈的过程,同时考虑每个用户均以个人利益最大化为目标。因此,无论是链接预测,推荐系统或是社团形成,其本质都是在个体利益最大化过程中达到的寻找博弈过程中达到的整体利益均衡状态,这为我们提供了一个新颖而有潜力的研究新思路。
除了本文介绍的博弈论在链接预测、聚类和网络形成分析的应用,博弈论在异构信息网络中还有其他巨大的价值等待研究者去挖掘与探索。如,在较为成熟的机器学习模型中加入博弈论的思想来提高模型效率或准确率。又如,结合博弈论的思想和传统的网络演化动力学模型来分析异构信息网络的演化过程,进行预测社群演化。综上所述,博弈论在数据挖掘研究领域具有巨大的研究价值,这也为研究者们提供了一个新颖的、有潜力的研究方向。
[1]Jackson M O,Zenou Y.Games on networks[J].Handbook of game theory,2014(4):1-89.
[2]Zhao T,Zhao H V,King I.Exploiting Game Theoretic Analysis for Link Recommendation in Social Networks[C]//ACM International Conference on Information Management,2015:851-860.
[3]Alqadah F,Bhatnagar R.A game theoretic framework for heterogenous information network clustering[C]//ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,2011:795-804.
[4]Yang Z,Chen W.A Game Theoretic Model for the Formation of Navigable Small-World Networks[C]//International Conference on World Wide Web,2015:1329-1339.
[5]Jackson M O.A survey of network formation models:stability and efficiency[J].Group Formation in Economics:Networks,Clubs,and Coalitions,2005,11-49.
[6]吴枝喜,荣智海,王文旭.复杂网络上的博弈[J].力学进展,2008,38(6):794-804.
WU Zhixi,RONG Zhihai,WANG Wenxu.Games on Complex Networks[J].Advances in Mechanics,2008,38(6):794-804.
[7]刘群,易佳.基于演化博弈的社交网络模型演化研究[J].物理学报,2013,(23):463-471.
LIU Qun,YI Jia.The research of the social network evolution based on the evolutionary game theory[J].Acta Physica Sinica,2013,(23):463-471.
[8]王龙,伏锋,陈小杰,等.复杂网络上的演化博弈[J].智能系统学报,2007,(2):1-10.
WANG Long,FU Feng,CHEN Xiaojie,et al.Evolutionary games on complex networks[J].CAAI Transactions on Intelligent Systems,2007,(2):1-10.
[9]Watts D J.Six Degree:The Science of a Connected Age[M].New York:Norton,2003.
[10]WattsDJ,StrogatzSH.Colectivedynamicsof small-world networks[J].Nature,1998,393:440-442.
[11]Watts D J.Small Worlds:The Dynamics of Newtorks Between Order and Randomness[M].New Jersey:Princeton University Press,1999.
[12]J.Tang,H.Gao,H.Liu,A.D.Sarma.eTrust:Understanding trust evolution in an online world[C].New York,NY:ACM.2012.253-261.
[13]Y.Dong,J.Tang,S.Wu,J.Tian,et al.Link prediction and recommendation across heterogenous social networks[C].Piscataway,NJ:IEEE.2012.181-190.
[14]J.Leskovec,D.Huttenlocher,J.Kleinberg.Predicting positive and negative links in online social networks[C].Berlin,German:Springer.2010.
[15]Chakrabarti D,Kumar R,Tomkins A.Evolutionary clustering[C].New York,NY:ACM.2006.554-560.
[16]Chi Y,Song X,Zhou D,et al.Evolutionary spectral clustering by incorporating temporal smoothness[C]. New York,NY:ACM.2007.153-162.
[17]Sarkar P,Moore A W.Dynamic social network analysis using latent space models[J].ACM SIGKDD Explorations Newsletter,2005,7(2):31-40.
[18]Lin Y R,Chi Y,Zhu S,et al.Facetnet:a framework for analyzing communities and their evolutions in dynamic networks[C].New York,NY:ACM.2008.685-694.
[19]Yang T,Chi Y,Zhu S,et al.Detecting communities and their evolutions in dynamic social networks—a Bayesian approach[J].Machine learning,2011,82(2):157-189.
[20]Yang T,Chi Y,Zhu S,et al.A Bayesian Approach Toward Finding Communities and Their Evolutions in Dynamic Social Networks[C].Philadelphia:SIAM.2009. 990-1001.
[21]Lin Y R,Sun J,Cao N,et al.Contextour:Contextual contour visual analysis on dynamic multi-relational clustering[C].Philadelphia:SIAM.2010.418-429.
[22]Tantipathananandh C,Berger-Wolf T,Kempe D.A framework for community identification in dynamic social networks[C].New York,NY:ACM.2007.717-726.
[23]Kim M S,Han J.A particle-and-density based evolutionary clustering method for dynamic networks[J].Proceedings of the VLDB Endowment,2009,2(1):622-633.
[24]侯彩芳.基于偏好的博弈学习与复杂网络的共演化机制的研究[D].长春:吉林大学,2016.
HOU Caifang.The Research of Co-Evolution Mechanism Between Complex Networks and Game Learning Based on Individual Preference[D].Changchun:JILIN University,2016.
[25]Zimmermann M G,Eguíluz V M,San Miguel M.Coevolution of dynamical states and interactions in dynamic networks[J].Physical Review E,2004,69(6):065102.
[26]Li W,Zhang X,Hu G.How scale-free networks and large-scale collective cooperation emerge in complex homogeneous social systems[J].Physical Review E,2007,76(4):045102.
[27]Helbing D,Yu W.The outbreak of cooperation among success-driven individuals under noisy conditions[J]. Proceedings of the National Academy of Sciences,2009,106(10):3680-3685.
Application of Game Theory in Social Networks
DAI Xiang
(Southwest China Institute of Electronic Technology,Chengdu610036)
The rapid development of online social networks has attracted great research interests in different fields.In Economics,researchers use game theory to analyze the mechanism of network formation which explains the reason of network formation,called network formation game.While in computer science,many mature algorithms and models have been proposed by researchers for community formation,link prediction,recommendation system etc.We mainly use these models and algorithms to recommend friends to users.Combing game theory with link prediction is of great significance to research on link prediction based on utility maximization theory.This article summarizes some achievements about the application of game theory in the study of link prediction and community formation in social networks,and demonstrates the meaning of game theory in network evolution.
social networks,game theory,link prediction,network evolution
TP311
10.3969/j.issn.1672-9722.2017.06.024
2016年12月3日,
2017年1月19日
国家自然科学基金项目(编号:61173099,61103043)资助。
代翔,男,博士,工程师,研究方向:自然语言处理、数据挖掘等。
——博弈论

