基于GNSS的飞行器姿态确定算法研究
刘帅赵国荣王元鑫曹唯一
(1.海军航空工程学院研究生管理大队烟台264001)(2.海军航空工程学院控制工程系烟台264001)(3.海军航空工程学院学员一旅烟台264001)
基于GNSS的飞行器姿态确定算法研究
刘帅1赵国荣2王元鑫1曹唯一3
(1.海军航空工程学院研究生管理大队烟台264001)(2.海军航空工程学院控制工程系烟台264001)(3.海军航空工程学院学员一旅烟台264001)
论文对基于GNSS的飞行器姿态测量进行研究。考虑姿态测量系统基线长度固定的特点,建立了单基线测量的载波相位差分姿态方程。在解算姿态方程时,为克服可能出现的载波相位观测值异常情况,提出了基于抗差卡尔曼滤波的飞行器姿态解算算法。仿真结果表明,该算法具有比最小二乘法更高的姿态解算精度和稳定性。
姿态测量;载波相位单差方程;抗差卡尔曼滤波
Class NumberTP301
1 引言
飞行器的姿态测量系统是其飞行控制系统的重要组成部分,姿态测量精度的提高对提高控制系统的稳定性和准确性具有重要意义。传统的姿态测量系统主要包括光学测姿系统、地磁导航系统、惯性导航系统等,都有其各自的局限性[1~2]。基于GNSS(全球导航卫星系统)的姿态测量是近年来发展迅速的研究领域,GNSS测姿具有适用性强、性价比高、无累积误差等优点,既可以作为独立的导航系统应用到飞行器的导航中,也可以与惯性导航系统等组合,进行组合导航的应用,具有广阔的应用前景。
现有的GNSS姿态解算算法主要可以分为三类:直接计算法、最小二乘法和卡尔曼滤波法。直接计算法是一种经典的方法,算法运算简单,已被广泛地应用于GNSS姿态测量系统的设计与研制中[3~4],但该方法在处理多基线系统时不能充分利用多基线提供的冗余信息,且解算结果容易受观测噪声影响。最小二乘法是一种经典的最优估计方法,在利用载波相位信息进行姿态解算时,如果整周模糊度已确定,则观测方程的数量往往大于未知数个数,此时运用最小二乘法可以很好地利用所有观测信息,尽可能地减少测量噪声的影响,得到最优估计[5~7]。卡尔曼滤波法是20世纪最伟大的学术成果之一,已经被广发地应用于导航、定位、信号处理、自动控制等多个领域,基于卡尔曼滤波的姿态解算可以有效地利用载体的运动特性,实现姿态的最优估计,但其结论是在系统噪声统计特性已知的前提下得到的,因而很难有效解决测量过程中可能出现的观测值异常问题。本文将在研究GNSS姿态测量原理的基础上,对传统的卡尔曼滤波算法进行改进,通过引入抗差因子,建立抗差卡尔曼滤波方程对状态向量进行估计,实现动态条件下的载体姿态快速解算。
2 载波相位差分测姿模型的建立
高精度的GNSS姿态测量,需要借助载波相位差分技术来实现。图1为单差载波相位示意图。
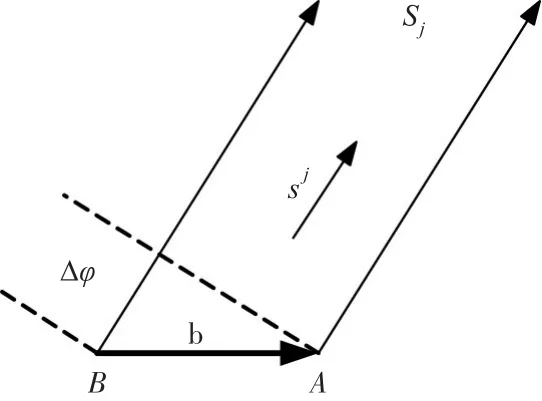
图1 单差载波相位示意图
假设某一时刻A、B两个天线同时接受卫星j的信号,在基线较短的情况下,可认为两天线的对流层延时等效距离误差和电离层延时等效距离误差相等,而接收机钟差引起的误差也可以通过共用接收机等方式加以消除。因此以A、B两个天线为端点的基线关于卫星j的单差载波相位方程可写成下列形式:
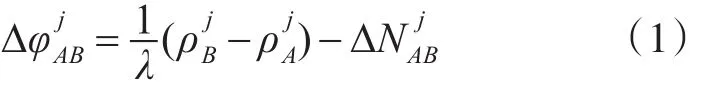
根据图1中的几何关系有:

式中:b为由主天线相位中心指向辅助天线相位中心的基线矢量;sj为卫星Sj的视线矢量。
假设卫星j的方向角和高度角分别为βj和 αj,载体的方位角和抚养角分别为ψ和θ,则有下式成立
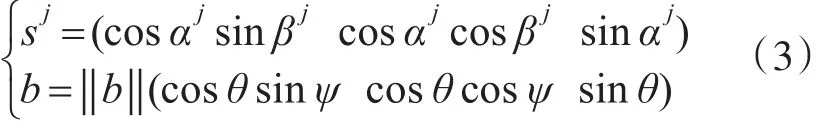
将式(2)、(3)带入式(1)可得单差观测方程的表达式:
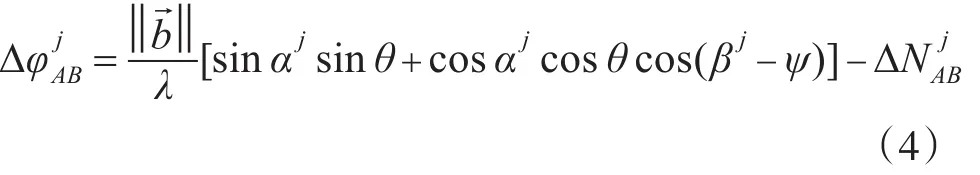
假设姿态角的初值为(ψ0,θ0),应用泰勒展开对式(4)进行线性化,有[8]:
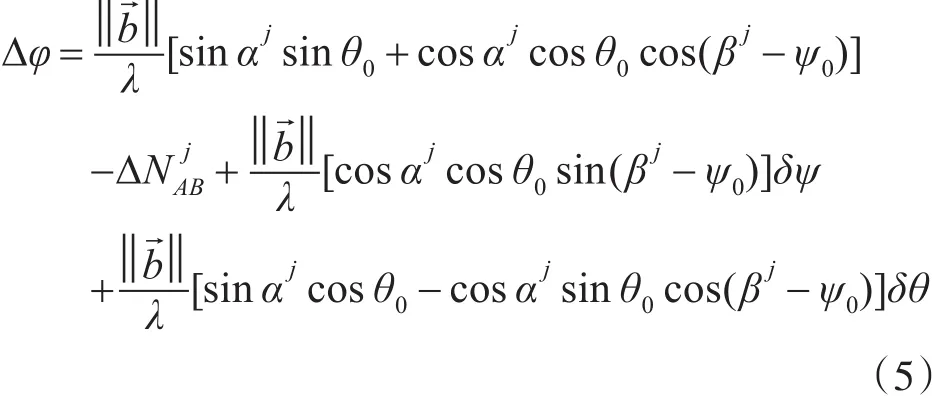
式(5)可以用下列矩阵形式表示:
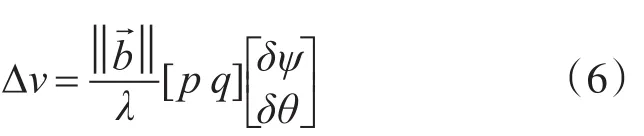
式中:
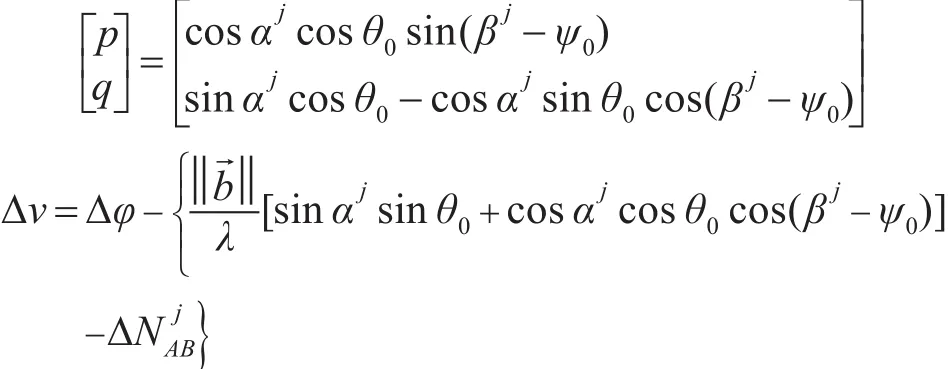
3 基于抗差卡尔曼滤波的姿态解算
3.1 系统状态方程和观测方程的建立
用ψk、θk表示在第k个历元的偏航角和俯仰角,用ψ̇k、θ̇k表示偏航角和俯仰角的变化率,则可构造状态向量矩阵Xk=(ψk,θk,ψ̇k,θ̇k)T。
结合式(6),可以得到如下的观测方程:

式中,Zk为观测矩阵,Vk为测量噪声序列,
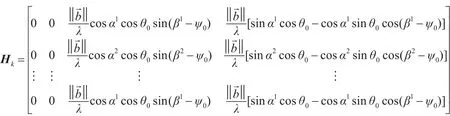
假设采用常速度模型,则状态转移方程为
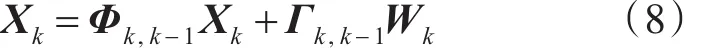
其中,Γk,k-1为系统噪声驱动阵,Wk为系统噪声序列,Φk,k-1为k-1时刻到k时刻的状态转移矩阵,且有:
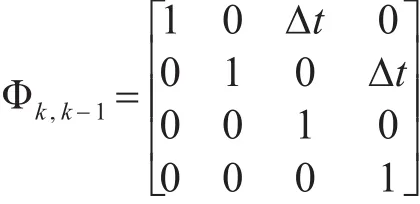
式(7)和式(8)共同组成了GNSS姿态测量系统的滤波方程:
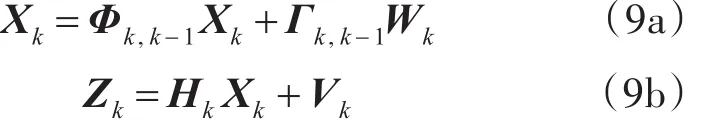
一般情况下,将测量噪声和系统噪声视为不相关的高斯白噪声,即有以下关系成立:
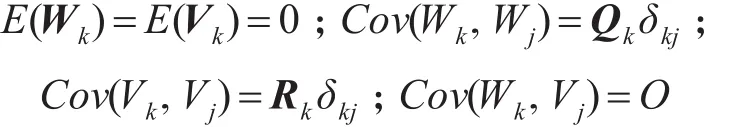
上式中,Qk代表系统噪声序列的方差阵,假设为非负定阵;Rk代表测量噪声序列的方差阵,假设为正定阵[9]。δ为狄拉克函数,k=j时,δkj=1,k≠j时,δkj=0。
3.2 姿态解算过程
滤波方程建立后,若使用经典卡尔曼滤波算法进行姿态解算,算法描述为[9]
状态一步预测:
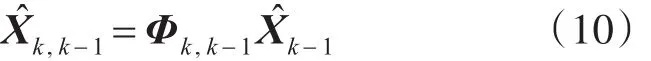
状态估计:
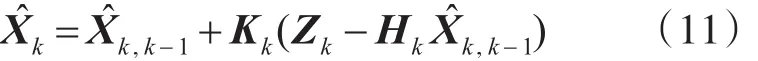
一步预测误差方差阵:
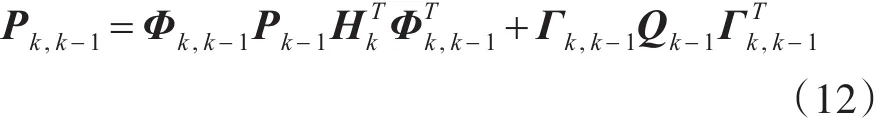
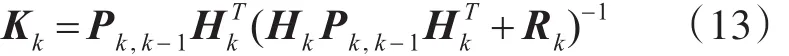
估计误差方差阵:
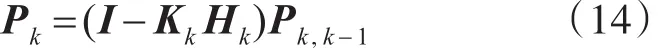
在给定初始值X̂0和P0的情况下,可以通过上述公式递推得到各个时刻的解算结果。
经典的卡尔曼滤波在处理只含有偶然误差的问题时,能够取得很好的效果,但对于存在粗差的情况,则可能出现结果偏离很大的情况。在基于GNSS的姿态测量中,在特定的时间、特定的地点,可能会由于多路径效应等因素导致观测值异常。因此,需要寻找一种能够有效规避异常观测值的方
滤波增益矩阵:法,抗差卡尔曼滤波算法采用抗差估计原理,通过引入降权因子改变了滤波增益矩阵,较好地解决了这一问题。
抗差卡尔曼滤波算法的滤波增益矩阵为
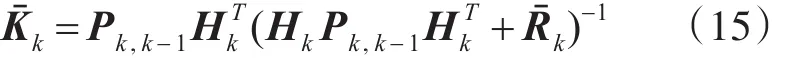
式(15)中的Rˉk为观测序列Zk的抗差等价协方差,假设观测序列的权矩阵为B=diag(b1,b2,…,bn),则Rˉk可以通过以下方法求得:
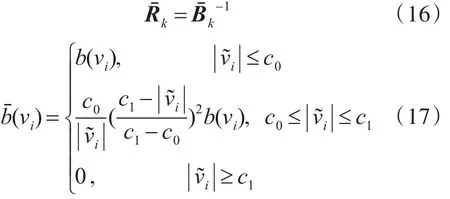
式中,c0和c1为常数,且c0取值范围一般为1.5~2.0,c1的取值范围一般为3.0~8.5,||v͂i为Zk的标准化残差[10]。
根据调整后的滤波增益矩阵抗,可得抗差卡尔曼滤波算法的估计误差方差阵:
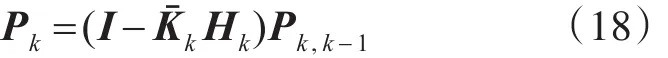
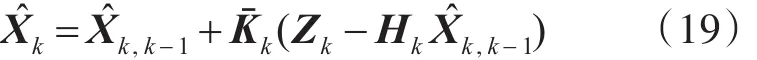
抗差卡尔曼状态估计:联立式(10)、(12)、(15)、(19)和(20),便得到了基于抗差卡尔曼滤波的递推方程,可根据初始值进行各个历元的姿态解算。
4 仿真及结果分析
使用单基线GNSS姿态测量系统对本文提出的算法进行仿真验证,基线长度设为3m,采集200个测量历元的载波相位观测数据,分别用最小二乘法和本文提出的抗差卡尔曼滤波算法进行姿态解算,解算结果如图3和图4所示。
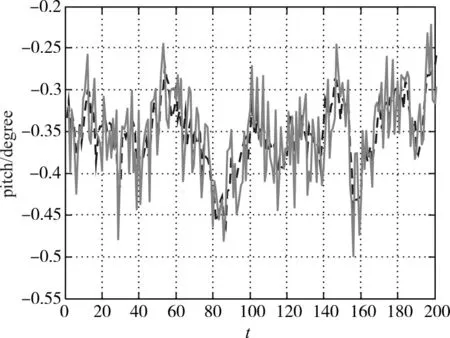
图3 俯仰角测量结果
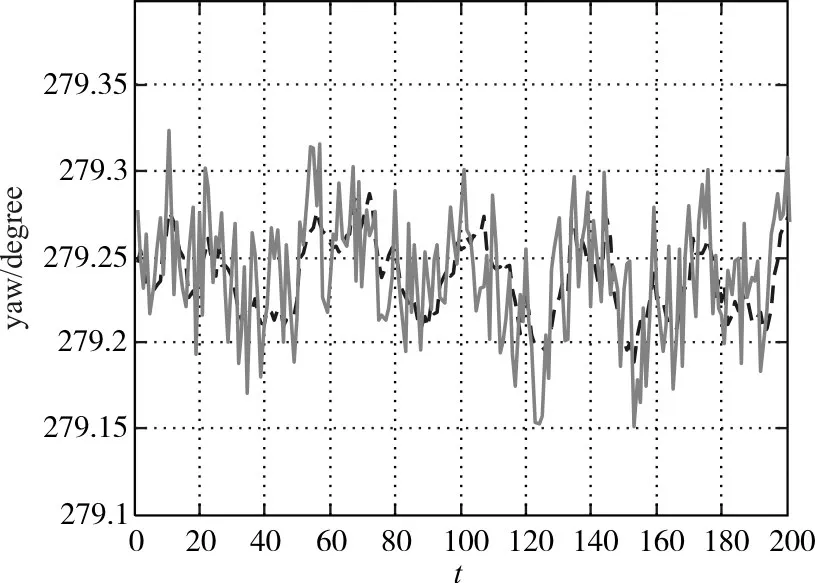
图4 偏航角测量结果
图中浅色线表示最小二乘法的姿态解算结果,深色线表示抗差卡尔曼滤波法的解算结果。从图中可以明显看出抗差卡尔曼滤波算法的解算效果要好于最小二乘法。为了使结果更为直观,对测量结果的最大值、最小值、方差进行统计,结果如表1所示。
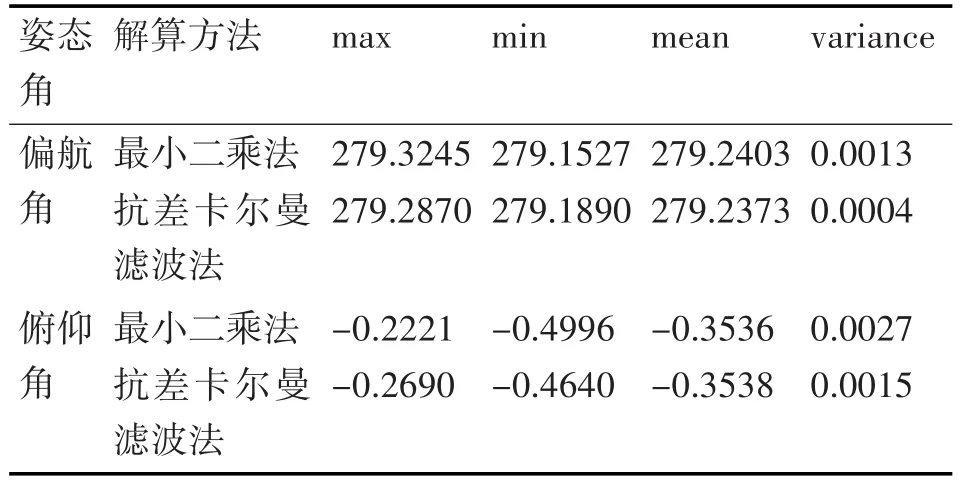
表1 两种方法的姿态解算效果汇总表
5 结语
本文针对基于GNSS的飞行器姿态测量问题,结合载体的运动特点建立系统状态方程和量测方程,采用抗差卡尔曼滤波算法解决测量过程中可能出现的载波相位观测值异常问题,仿真结果表明算法具有较高的解算精度和可靠性,具有较好的工程应用的前景。
[1]许江宁,朱涛,卞鸿巍.GPS姿态测量技术综述[J].海军工程大学学报,2003,15(3):19-20.
XU Jiangning,ZHU Tao,BIAN Hongwei.Review on GPS attitude determination[J].Journal of Naval University of Engineering,2003,15(3):19-20.
[2]李跃,邱致和.导航与定位[M].北京:国防工业出版社,2008.
LI Yue,QIU Zhihe.Navigation and positioning[M].Beijing:National Defense Industry Press,2008.
[3]T.Scatahlini,F.Pagola,J.Cogo and J.G Garcia.Attitude estimation using GPS carrier phase single differences[J].IEEE LATIN AMERICA TRANSACTIONS,2014,12(5):847-853.
[4]郑坤,董绪荣,刘亚涛.GNSS载波相位多天线实时测姿系统的设计与实现[J].测绘科学技术学报,2014,31(2):136-140.
ZHENG Kun,DONG Xurong,LIU Yatao.Attitude Determination with A GNSS Multiple-Antenna System[J].Journal of Geomatics Science and Technology,2014,31(2):136-140.
[5]Teunissen P J G.A general multivariate formulation of the multi-antenna GNSS attitude determination problem[J]. Artificial Satellites,2007,42(2):91-111.
[6]张健.基于GPS的航天器姿态确定研究[D].哈尔滨:哈尔滨工业大学,2009.
ZHANG Jian.Study on attitude determination of spacecraft based on GPS[D].Harbin:Harbin Institute of Technology,2009.
[7]王冰,隋立芬,张清华.利用GPS解算载体测姿的算法研究[J].武汉大学学报(信息科学版),2013,38(12):1392-1396.
WANG Bing,SUI Lifen,ZHANG Qinghua.Research on attitude determination algorithm using GPS[J].Geomatics and Information Science of Wuhan University,2013,38(12):1392-1396.
[8]王永泉.长航时高动态条件下GPS/GLONASS姿态测量研究[D].上海:上海交通大学,2008.
WANG Yong-quan.GPS/GLONASS attitude determination research under long endurance and High Dynamic Conditions[D].Shanghai:Shanghai Jiao Tong University,2008.
[9]卞鸿巍,李安,覃方君,等.现代信息融合技术在组合导航中的应用[M].北京:国防工业出版社,2010:70-77.
BIAN Hongwei,LI An,TAN Fangjun.The use of modern information fusion technology in integrated navigation[M].Beijing:National Defense Industry Press,2010:70-77.
[10]闫欣.基于抗差估计的GPS/MIMU组合导航滤波算法研究[D].哈尔滨:哈尔滨工程大学,2010.
YAN Xin.Research on the filter algorithm of GPS/MIMU integrated navigation based on robust estimation[D]. Harbin:Harbin Engineering University,2010.
Aircraft Attitude Determination Method Based on GNSS
LIU Shuai1ZHAO Guorong2WANG Yuanxin1CAO Weiyi2
(1.Graduate Students'Brigade,Naval Aeronautical and Astronautical University,Yantai264001)(2.Department of Control Engineering,Naval Aeronautical and Astronautical University,Yantai264001)(3.Students'Brigade one,Naval Aeronautical and Astronautical University,Yantai264001)
This paper mainly studies on the attitude determination of aircraft based on GNSS.Considering the fact that the baseline of attitude determination system is fixed,the carrier phase single difference equation is build to compute the attitude.A method based on the robust kalman filtering is presented to solve the problem of gross error in measurement data.The simulation result shows that the precision and reliability of the presented method is better than the least squares method.
attitude determination,carrier phase single difference equation,robust kalman filtering
TP301
10.3969/j.issn.1672-9722.2017.06.014
2016年12月18日,
2017年1月23日
刘帅,男,硕士,研究方向:飞行器综合导航。赵国荣,男,博士,教授,研究方向:导航制导与控制。王元鑫,男,硕士,研究方向:飞行器综合导航。曹唯一,男,研究方向:飞行器导航与控制。

