基于正态分布的轴类零件测量误差数据处理分析

黄 毅，肖明涛

（1.湘西民族职业技术学院，湖南 吉首 416000；2.湖南农业大学，湖南 长沙 410128）

基于正态分布的轴类零件测量误差数据处理分析

黄 毅1，肖明涛2

（1.湘西民族职业技术学院，湖南 吉首 416000；2.湖南农业大学，湖南 长沙 410128）

在零件加工测量过程中，因测量环境、测量人员、测量方法等多方面的原因，总存在测量误差。文章对轴类零件测量误差产生的原因及随机误差的分布规律进行了分析，依据随机误差正态分布规律，分析随机误差与标准偏差的关系，通过对直接测量列的数据处理，得出接近真值的测量结果，提高轴类零件的测量准确度。

随机误差；标准偏差；数据分析

在轴类零件加工测量过程中，因环境等多方面的原因，测量结果不可能绝对准确，只能得到接近真值的数值，总会存在一定的误差，称测量误差，测量误差影响测量结果的精度和准确度。如表1对某轴进行等精度测量，如何求其测量结果，文章依据随机误差的正态分布对测量数据进行分析。

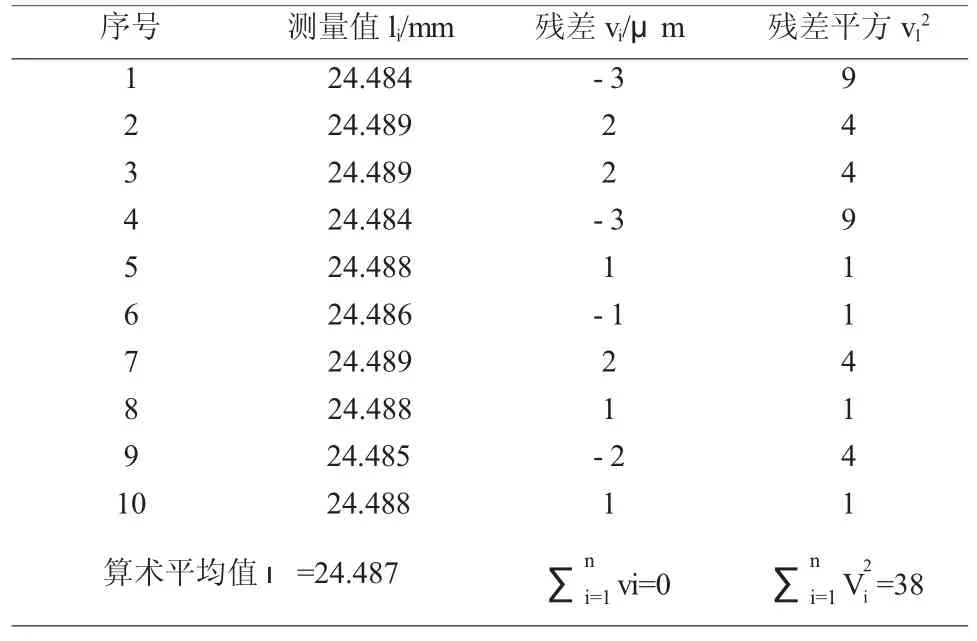
表1 某轴的数据测量表

1 测量误差产生原因分析

很多因素都可以导致测量误差产生，但主要有以下方面的误差产生因素。一是测量环境变化引起的误差。因物体的热胀冷缩属性，温度的变化极易引起测量误差，因此很多高精度的测量和装备都在恒温下完成。二是测量人员因视力、读书不准确、操作技术等主观原因引起的误差。三是测量方法的不

完善、测量手段缺陷和测量仪器的不稳定所引起的测量误差。

2 测量误差分析

测量误差指测量结果与被测量的真值的代数差，它反映测量结果偏离测量真值的大小程度，其表达式为：

式中，δ为测量误差，ι为实测量值，μ被测量真值。由式（1）可知，测量误差δ越接近零，实测量值越ι越接近真值μ，测量所得精度和准确度越高。但在实际加工测量中，真值μ是很难得知的，一般以高精度的测量所得值（算术平均值）为相对真值。

3 随机误差分析

随机误差也称为偶然误差，是由于在测量过程中一系列有关因素微小的随机波动而形成的具有相互抵偿性的误差，它是不可避免和无法消除。为了减小随机误差对测量结果影响，可用概率论和数理统计估计随机误差大小和规律，对数据结果进行处理。对某一轴类零件在同一条件下进行测量测，测量得数据分别为

ι1，ι2，…，ιi，被测量真值为ι，其相应随机误差为：通过大量的数据实验证明，随机误差δi基本上服从正态分布，其概率密度函数为：

式（3）中，y为概率密度；e为自然对数底数；δ为随机偏差；σ为均平方根差（标准偏差），平方根差与随机误差关系如下。

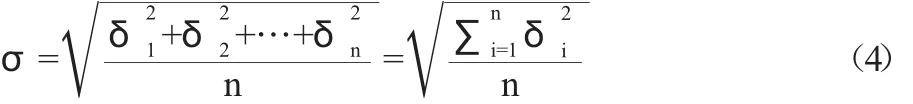
式（4）中，n为测量次数，其正态分布曲线为图1所示。

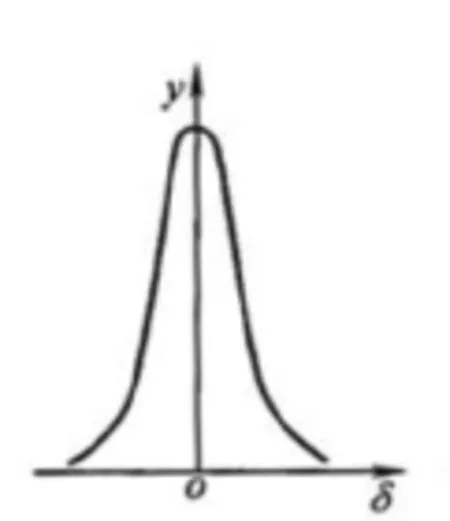
图1 正态分布曲线

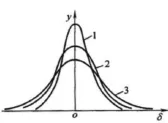
图2 均平方根差对随机误差分布特性影响

由图1、2分析，σ1<σ2<σ3，则y1max>y2max>y3max，标准偏差σ越大，曲线越缓和，随机误差δ越集中，可靠性越低；反之，可靠性越高。

4 随机误差与标准偏差关系分析

基于概率论对图2进行分析，正态分布曲线下所包含的全部面积总和等于随机误差δi出现的概率P总和，即可得

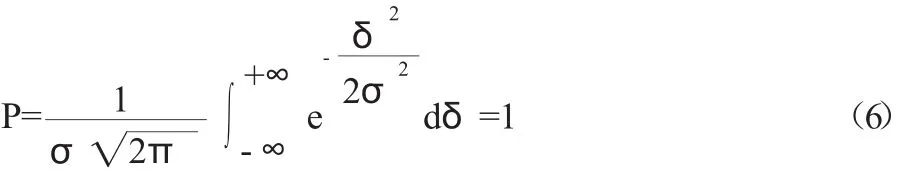
由公式（2）、（5）可得：随机误差落在（+δ，-δ）之间的概率为：

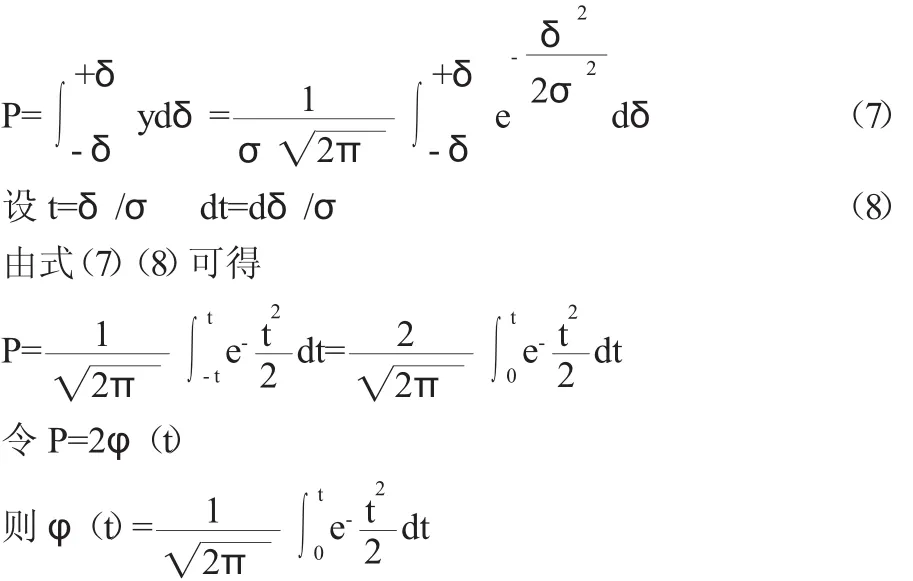
函数φ（t）称为概率积分函数（拉普拉斯函数）

由正态分布积分表得，随机误差落在±1σ的概率为68.26%，落在±2σ，范围内概率为95.44%，落在±3σ范围内的概率为99.73%，因此对于有限次数的测量，通常把±3σ作为单次测量的随机误差的极限值，即

单个测量值表示结果为：算术平均测量值表示结果为：

5 测量数据处理

现对零件进行多次等精度数据测量，测量得数据分别为ι1，ι2，…，ιn，其多次测量的算术平均值为：

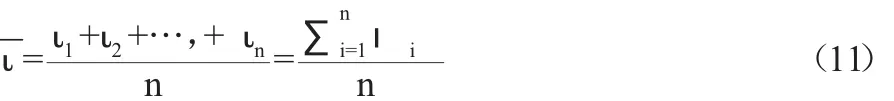
由表1和式（11）得：

随机误差δ1=ι1-ι，δ2=ι2-ι，…，δn=ιn-ι，

误差相加得

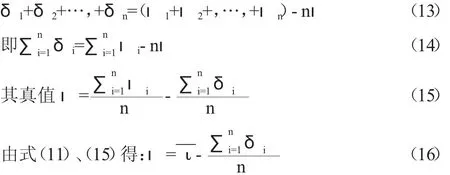
因随机误差存在抵偿性（如表1所示），

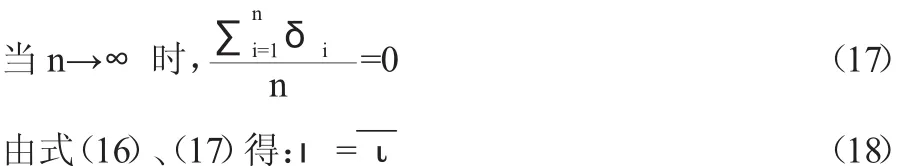
即算术平均值代替真值；在测量中把算术平均值 ι代替真值ι所计算的误差称为残差vi。

即残差代替随机误差

在实际测量中，因真值ι和随机误差δi未知，任一测得值的标准偏差σ估值为各误差平方和的平均数的平方根，标准偏差用残差vi估算，可表示为：

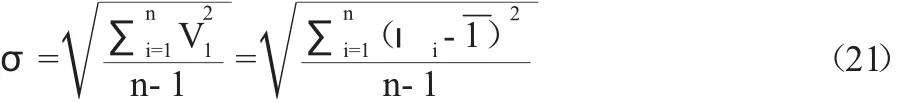
由表1和式（21）得:

而在多次重复测量中，算术平均值1的可靠性要高于单次测量结果ιi，依据误差理论在等精度测量时:

由式（22）（23）算术平均值量标准偏差

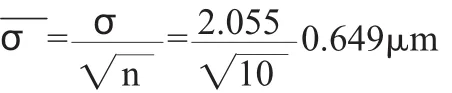
对于有限次测量来说，随机误差超出±3σ的可能性为零，因此将±3σ作为随机误差的极限值，表达为3σ，即单个测量极限误差 σlim=±3σ=±6.165μm。算术平均值测量结果误差为

由式（10）得轴得直径测量结果为：

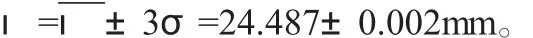
6 结语

在进行轴类零件数据误差处理分析时，首先计算算术平均值，然后通过列表计算残差vi，通过残差计算列单次标准偏差σ，再通过单次标准偏差计算列算术平均值标准偏差最后依据偏差的正态分布特点，确定测量结果。

［1］胡照海.零件集合测量检测［M］.北京：北京理工大学出版社，2015.

［2］机械设计手册［M］.北京：化学工业出版社，2004.

［3］胡照海.零件集合测量检测［M］.北京：北京理工大学出版社，2015.

［4］吴蔚.园零件测量的数据处理［J］.中国：计量学报，1986，（2）.

［5］林玉池，刘治军，吴敬国．轴类零件参数综合检测［J］．中国机械工程，2000，11（3）：295-297．

Data Analysis of Measurement Error of Shaft Parts Based on Normal Distribution

HUANG Yi1，XIAO Min-tao2
（1.Xiangxi National Vocational and Technical College，Jishou，Hunan 416000，China；2.Hunan Agricultural University，Changsha，Hunan 410128，China）

In the process of part processing and measurement,there are always measurement errors due to the measurement environment，the measurement personnel，the measurement method and so on.In this paper，the causes of the measurement errors of the shaft parts and the distribution of the random errors are analyzed.According to the regular distribution of random errors，the relationship between the random error and the standard deviation is analyzed.By analyzing the data of the direct measurement column，value of the measurement results has obtained to improve the accuracy of the measurement of shaft parts.

random error；standard deviation；data analysis

文献标识码：A 文章编号：2095-980X（2017）04-0063-02

2017-04-05

2016年教育厅科学研究项目（16C1590）。

黄毅（1980-），男，湖南龙山人，硕士，教师，主要研究方向：职业教育教学模式改革及农业机械机构创新设计。