基于加权类分数傅立叶变换的变换域通信系统
梅林+房宵杰+沙学军

中图分类号:TN929.5 文献标志码:A 文章编号:1009-6868 (2017) 03-0038-007
摘要:
提出单载波与多载波技术体系的融合将会成为未来通信系统空中接口技术发展的重要趋势,指出对既有系统与技术的兼容性和扩展性是混合单、多载波系统所需重点关注问题。结合扩频、均衡、部分快速傅立叶变换(FFT)解调等技术,论述了干扰平均化思想在混合载波系统抗衰落、抗干扰中的重要作用,并展望了加权类分数傅立叶变换(WFRFT)通信系统相关技术的未来研究重点。
关键词:WFRFT;混合载波体制;时频双弥散信道;低截获概率
Abstract: This paper indicates that the convergence of single carrier and multi-carrier technological system will be the general trend for the air interface of future communications systems, and the compatibility and expansibility should be the crucially focused features. The idea of averaging interference for the hybrid carrier system over fading and interference channels are discussed along with the combinations of hybrid carrier system and other techniques such as spectrum spreading, equalization and partial fast Fourier transform (FFT) demodulation. Future work for the research of weighted-type fractional Fourier transform (WFRFT) communications system and relative technologies are also addressed.
Key words: WFRFT; hybrid carrier scheme; time-frequency doubly dispersive channel; low probability of interception
通信过程中存在的系统、信号、干扰等都已由时、空、频、能量等物理关系抽象出的数学工具和模型来表征、分析。在这些通信过程所依赖的资源中,时间与频率这一对物理量最为人们所熟悉,通信中遇到的许多问题最终都可以归结为时频资源受限以至无法同时满足时、频域约束条件的矛盾。传统通信理论中所孤立使用的数学工具,已经无法简单、准确地描述新需求背景下复杂的时频关系。其中最为典型的就是高速移动环境下的宽带无线接入问题,即在高运动速率、高数据速率背景下进行可靠传输的问题。在此背景下,信道呈现一种“双弥散”的特性,即由多径造成的时间弥散和由多普勒频移造成的频率弥散。在实际操作中,通常很难同时抑制两种干扰。针对移动系统来说,主要问题就是要设计出有效的对抗时频双选择性衰落的相关技术。
传统的理论与方法是基于傅立叶分析,在时频域分别处理,一定程度上联合时频处理的结果。文中,我们所介绍的研究将解决方法从传统的傅立叶变换域扩展到了加权分数傅立叶变换(WFRFT)域。一方面,在理论上傅立叶分析将作为WFRFT的一个特例;另外一个方面,在WFRFT域信号的时频分量将融合为一个整体,为解决这一类“时频联合”或“时频协同”问题,提供了新的理论根据。
1 加权类分数傅立叶变换
归一化的傅立叶变换是一种酉变换,具有周期为4的特点。Hermite-Gauss函数是傅立叶变换的特征函数,其对应的特征值有4个:1、、-1、(表示虚数单位),对应单位圆上角度为0、、和的点。分数傅立叶变换(FRFT)是对传统傅立叶变换的推广,Hermite-Gauss函数同样也是FRFT的特征函数,而其对应的特征值是在单位圆上按照某种规律采样的结果。以作为一个单位,FRFT特征值对应的角度一般不在整数倍的位置上。因而,FRFT之所以被称作“分数”的原因,也可以从傅立叶变换特征值分数化的角度来解释。
不同的特征值分数化方法,对应了不同类型的FRFT。由线性调频信号(或称chirp信号)构成这种FRFT的基函数,所以这种FRFT也被称为“chirp类FRFT”,简称CFRFT。CFRFT出现最早,因而很多时候CFRFT也被直接称作FRFT。
FRFT有很多性质,其中线性、酉性、分数阶可加性、阶数周期性及特征值的周期性、边界性等性质尤为重要,以致于这些性质足以构成对FRFT的完整描述。1995年,C. C. Shih利用傅立叶变换周期为4的特点,通过将函数自身及其反转、函数的傅立叶变换及其反转作为态函数进行加权组合,得到了一种具有上述FRFT重要性质的新变换,后来这种FRFT即被称作WFRFT。C. C. Shih提出的WFRFT定義,无论从形式上还是具体数值计算上都与之前出现的CFRFT不同。至此之后,更多广义形式的FRFT定义被提出,CFRFT与WFRFT之间的关系也逐渐被人们所揭示[2-4]。
由于CFRFT具有形式相对简单的基函数(chirp函数),其物理含义也较明确,故而在光学、信号处理、通信等领域有较多的应用研究。WFRFT提出伊始,由于和CFRFT的显著差异,加之基函数、物理含义不如CFRFT一样易于理解,故而只在图像加密方向上有少许应用研究成果。自2007年起,通过对WFRFT自身特点的研究,以及主流通信系统模型的对比,我们逐渐发现WFRFT在数字通信系统中具有特殊的物理含义,并由此产生了一种新的数字通信系统模型。
2 WFRFT通信系统模型及
其信号特征
2.1 WFRFT在数字通信系统中的
物理意义及其结构
C. C. Shih的原始定义是针对连续函数及其傅立叶变换而提出的,事实上,WFRFT中的加权系数可以用来定义任何一种具有周期特性(或者说“对称特性”)的变换。在提出WFRFT的最初文献中[1],Shih就利用正余弦函数的微分具有周期性的特点,提出了一种针对正余弦的“分数阶微分运算”。由此,利用归一化离散傅立叶变换(DFT)也具有周期为4的特点,可以利用Shih提出的加权系数,直接定义一种“加权DFT”,即序列的WFRFT。
设为任意复数序列,其归一化DFT定义为:
(1)
它可以进一步表示为一种矩阵的形式:
(2)
其中:
称作“ 傅立叶矩阵”或“DFT矩阵”,。
的WFRFT定义为:
(4)
WFRFT的矩阵定义为:
(5)
其中表示阶单位阵,阶反转阵定义为:
(6)
加权系数的定义有很多种不同的形式,公式(7)给出了其中较为广义的一种定义:
其中,是不小于3的整数(当取1或2时FRFT将退化而缺乏实际意义),,,。当、时,公式(7)退化为C. C. Shih所给出的原始加权系数定义。此时WFRFT由4个被加权函数和一个参数所确定,因而也被称作“单参数四项加权分数傅立叶变换”。
需要注意的是:上述定义的对象是无具体物理含义的序列,如利用上述定义计算连续函数的WFRFT则还需满足具有时频对称性的采样条件并采用离散数值算法实现[5]。
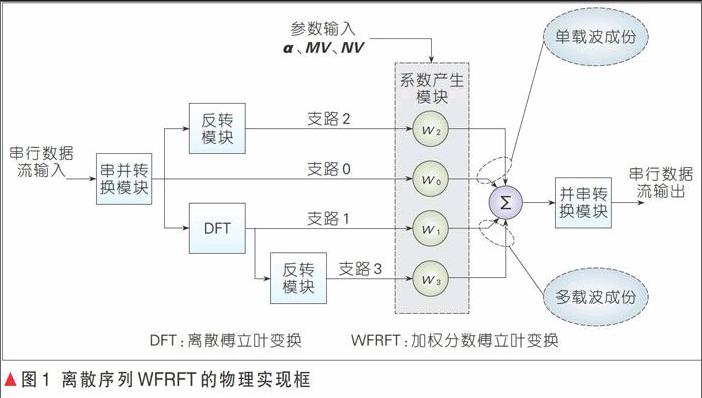
如果将视作完成相移键控(PSK)、正交振幅调制(QAM)基带映射后的信息符号,则WFRFT的物理实现流程如图1所示[6]。对比正交频分复用(OFDM)系统和单载波频域均衡系统的实现结构不难看出:图1中和支路包含有DFT模块,对应了OFDM信号的并行传输方式;而和支路没有DFT模块,实际上是简单的单载波串行传输过程。需要说明的是:DFT与离散傅立叶逆变换(IDFT)在OFDM发射机中的作用是相同的,在提出数字OFDM最初实现方式的文献中[7],发射机端正是使用的DFT而非IDFT。后人用IDFT替换DFT作为OFDM的调制实现方式,使得这一过程的物理意义更加清晰,但二者的本质却是相同的,在具体的工程实现上也是近乎一样的。
基于WFRFT在数字通信中具有的物理意义,文献[5]、[8]提出了“单载波、多载波融合通信系统”或称“混合载波通信系统”的概念。该通信系统模型可以在基于块传输方式的单载波和OFDM系统之间实现平滑过渡:当参数为偶数时系统对应单载波;当参数为奇数时系统对应多载波;当参数为非整数时系统对应单载波和多载波的混合形式。这一方面可以作为沟通传统单载波、多载波体制的桥梁;另一方面,在很多复杂、多变的环境或条件约束下,混合载波通信系统具有较传统载波体制更灵活的应对方式和更好的性能表现。
单载波与多载波在技术体系上的竞争由来已久,但长期演进(LTE)系统在上、下行链路分别采用不同的载波体制这一事实,则印证了两种技术体系可以相互融合的可能。未来通信系统将采用哪种技术体系以及在单载波、多载波之外会否有新的技术体系出现?从目前正展开的5G技术研发和标准制订中,这些问题的答案可见端倪。在5G备选技术热点中,广义频分复用(GFDM)、通用滤波多载波(UFMC)等新型多载波技术都宣称具有了对单载波技术体系的兼容和过渡方式。随着软件定义的、统一的空中接口成为一种趋势,单载波与多载波技术体系的融合与统一也势必成为未来技术的主流。
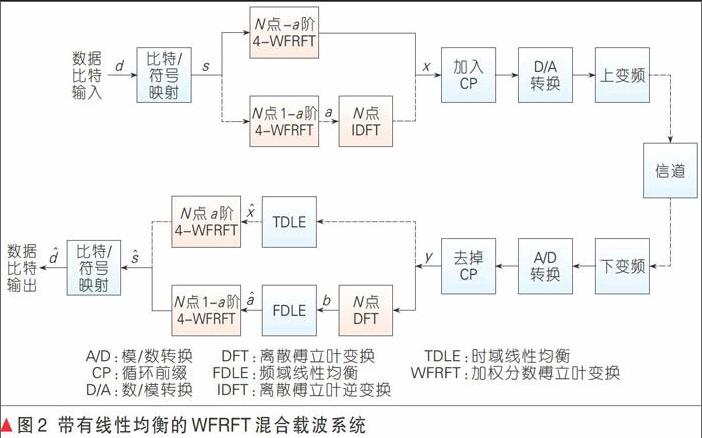
作为一种新型的混合载波通信技术或者融合技术方案,首先需要说明的是对既有技术体系的兼容性或适用性,其次则要提出可能的潜在优势或拓展技术方案。图2给出了WFRFT混合载波系统的线性均衡实施方案。均衡作为抵抗信道衰落的有效手段,其作用在时域还是频域依据的是信道的描述方式,而与信息调制的作用域没有关系。如同OFDM的信息可视作在频域进行调制,而单载波的信息是在时域进行调制,但OFDM与单载波都可以采用频域均衡技术,因为频率选择性衰落信道可以通过信道的频域矩阵进行描述。利用WFRFT的边界性(参数取整数时等效为做次傅立叶变换)和参数可加性()可以很容易地得到图2模型。WFRFT混合载波系统对信道估计与均衡、多址、波形等既有技术具有很好的兼容性[5],[8]。
2.2 WFRFT的信号特征
作为单载波和多载波的混合形式,WFRFT信号同时包含有单载波信号和多载波信号的特点。随着参数的改变,WFRFT的信号特征也在单载波信号与多载波信号之间连续变化。文献[6]、[8]从信息能量的时频分布特性入手,指出WFRFT信号比传统单载波和多载波信号具有更均匀的时频能量分布。这一分布特性有利于信号在复杂多变的场景中,以及时频域同时存在干扰的信道下保持性能鲁棒性。
文献[9-10]则通过信号星座图的描绘,展现了WFRFT信号灵活多变的特点。单参数WFRFT信号的星座圖会随着的改变而呈现发散、旋转、汇聚等变化,星座点分布呈现类高斯特性;多参数WFRFT信号的星座图甚至会出现星座点分裂的现象,使得正交相移键控(QPSK)信号看起来更像一个经过旋转、叠加噪声的16 QAM信号。WFRFT信号星座图的变化,使其对于非目的接收机而言更难检测,进而有利于提高通信信号的抗截获特性。从信号星座图的特点出发,为了进一步研究WFRFT信号与高斯信号的相似性,文献[9-10]对比了WFRFT信号实部/虚部的统计特性与正态分布的趋近程度和趋近条件。文献[11]最终分析得到了WFRFT信号概率密度函数的解析表达式,信号的概率密度函数可以用来推导信道容量、误码率、峰均功率比(PAPR)等指标的闭合表达式,为客观评价信号体制性能,求解最优参数提供理论基础。
此外,文献[12-13]研究了WFRFT信号的PAPR、带外功率抑制以及抗频偏鲁棒性等问题和相关技术,以期在多个不同优化目标的驱动下形成一套WFRFT信号设计、处理与参数优化的技术手段和方法。
3 WFRFT系统的抗衰落与
抗干扰技术
文献[5]和[10]在简化的选择性衰落信道模型下首先论证了WFRFT混合载波信号的优势;但这种信道模型过于抽象和简单,与实际信道和常用信道模型脱离较远。而在更复杂、恶劣的信道环境下过高的误码率会降低系统的实用性,因而后续很多研究试图通过将WFRFT与各种抗干扰技术相结合,以在更贴近实际的场景下获得抗干扰性能的优势。相关研究一方面涉及了混合载波系统的抗干扰技术,更重要的是要解决如何选取WFRFT参数的问题[6],[14-15]。前者可从单载波和多载波系统的相关技术设计方法中得到启发;而后者使得的“干扰平均化”的思想值得借鉴。
3.1 干扰平均化
所谓“干扰平均化”是指:将系统总体干扰能量尽可能平均地分散到各个子载波或判决位置上,以换取系统整体性能的提升。该方法实施的前提是系统总体干扰水平较低,否则该方法会起到相反的效果。干扰平均化思想的示意如图3所示,其中“残余干扰”这里指窄带系统的带外功率辐射。此处考虑的是一个宽窄带系统共存的场景,在其他场景中残余干扰也可以是由信号非正交、时频同步失真、信道估计误差、信道衰落、保护带不足等因素所引起的其他信号失真。使得干扰能量平均化的技术手段包括时频资源重组以及各种变换域手段,例如文献[6]在窄带干扰信道下分析了WFRFT参数的影响,文献[16]中采用了与扩频技术相结合的方式,文献[17]则针对时频双选信道研究了WFRFT系统与均衡技术的结合。
3.2 简化选择性衰落信道模型下
不同载波体制误码率性能比较
本节采用文献[5]和[18]中的“加性高斯白噪声(AWGN)+时/频域陷波”的简化选择性衰落信道模型来说明WFRFT系统在干扰信道下的鲁棒性。该模型在时频域某些点上存在深衰落,而在其他点上保持不变。由此可以建立基于该假设的3个基础模型:有一个时域深衰落点;有一个频域深衰落点;时频域各有一个深衰落点。本节仿真采用二进制相移键控(BPSK)调制,快速傅立叶变换(FFT)点数128,单参数4-WFRFT的参数。3种不同选择性衰落的参数如下:信道A的频域随机点幅度衰减10 dB;信道B的时域随机点幅度衰减10 dB;信道C的时频域各一个随机点,幅度分别衰减10 dB。
在图4 a)—c)中分别给出了单载波、OFDM和WFRFT3种不同载波体制系统在3种典型的简化选择性衰落信道模型下的性能比较。其中,单载波和OFDM系统在某一种信道下具备最优的系统性能,而在另外两种信道条件下都出现了误码平层,这一误码平层产生的原因正是深衰落点处噪声的影响。对于BPSK调制而言,OFDM系统位于频率深衰落点处的子载波误码率为50%;同理,單载波系统位于时域深衰落点处的符号判决错误概率也为50%,根据仿真参数可计算得到误码平层约在410左右。对于不在深衰落点所存在域上进行判决的系统,深衰落点的影响将会被128点“平均化”。当FFT点数足够多,或者深衰落点处影响在被平均化后尚不影响其他位置判决时,进行平均化的系统要比不进行平均化的系统具有更佳的性能;平均化程度越高的系统,系统性能越好。图4 d)将a)—c)中WFRFT系统的曲线绘制在了一起,可以发现WFRFT 系统在3种信道条件下的性能保持稳定。即便信道深衰落点数由1个增加到2个,系统性能也仅仅下降1 dB左右。
以上分析说明了WFRFT系统具备更好的信道适应能力。在复杂多变的信道条件下,特别是时间频率双选择性衰落的条件下,这一性能可以使WFRFT系统以较小的代价来换取相同的系统性能。WFRFT系统性能稳定的特点,适用于那些可以牺牲部分通信质量来换取长时间稳定通信的场合。
3.3 WFRFT与CDMA/直接序列扩频
技术的结合
在WFRFT混合载波系统的想法提出之后,文献[16]、[19-20]首先将其与码分多址(CDMA)/直接序列扩频技术结合在一起,希望通过扩频增益来提升系统整体误码率性能。
混合载波系统与CDMA技术结合可以有两种不同的方案。在混合载波-码分多址(HC-CDMA)传输方法中,在FRFT域进行序列扩展后采用WFRFT将信号变换到时域传输,传输信号均具有混合载波的特征,同时序列扩展进一步起到了符号能量平均化的作用。在这样的条件下,干扰能量被平均分配到更多的码片上,从而起到对多径干扰及单频干扰的抵抗作用。而信道衰落对扩频序列正交性的破坏将导致多用户干扰,为了抑制这种干扰并兼顾混合载波的特性,又提出在时域进行序列扩展的多载波直接序列码分多址(MC-DS-CDMA)方法。
3.4 时频双选择性衰落信道下
WFRFT系统的均衡技术
针对双选信道的时频双弥散特性,以及其在单载波(SC)和多载波(MC)系统中造成的不利影响,近年来的研究工作提出了多种双选信道下采样间/载波间干扰(ISI/ICI)的抑制方案,甚至利用多普勒扩展的信号频域分集特性,以提高系统在这种严苛信道条件下的检测性能。双选信道的干扰抑制方案主要可分为ICI抑制技术、信道均衡技术以及新型的信号调制/解调技术3种。ICI抑制技术包括脉冲成形和时域窗滤波两种方法;信道均衡包括线性均衡和非线性均衡两种形式;针对双选信道提出的新型调制解调技术包括能量扩展变换(EST)调制、部分FFT解调技术等。
文献[21-24]将WFRFT混合载波系统与双选信道下的均衡技术相结合,针对不同时变特性的双选信道,提出了结合时域窗滤波和信道均衡的多种干扰抑制方法,更好地实现了ISI和ICI的有效抑制和系统误码性能的提升。
文献[21]针对小多普勒频移的双选信道,提出了基于WFRFT的混合载波线性均衡方法,与传统单载波和多载波体制下线性均衡相比,这种方法利用WFRFT的能量平均化特性,有效地降低了残余干扰幅度在WFRFT域上的概率峰值,进而降低符号判决时大估计误差的出现概率,从而有效改善了系统的误码性能。文献[22-23]针对大多普勒频移的双选信道,结合WFRFT域先验信息的迭代反馈,提出了WFRFT混合载波体制下的时域迭代最小均方误差均衡方法。考虑到干扰抑制方法的实现开销,文献[24]提出了WFRFT混合载波体制下的频域迭代最小均方误差均衡方法,获得了优于传统载波体制下的误码性能,且与混合载波调制(HCM)下的时域迭代最小均方误差均衡方法相比,实现复杂度有明显的降低。
图5描绘了WFRFT混合载波双选信道下协同分数域均衡方法的设计思路:抗衰落的均衡技术仍旧在传统的时、频域实施,与传统技术不同的是WFRFT混合载波系统在分数域进行信号的判决和解调,并将计算得到的软信息通过域变换再反馈给时域或频域的均衡器进行迭代均衡[25]。
3.5 WFRFT系统与部分FFT的结合
文献[25-27]将WFRFT混合载波系统与部分FFT解调相结合,利用了混合载波系统能够将信号能量和干扰能量均匀分布在时频平面上的特点,以及部分FFT解调可以将来自信道的载波间的干扰分布到许多无用信号上的特征,从而减少了有用信号上的干扰。
文献[28]将部分FFT解调应用到了OFDM系统中,但是由于OFDM在快速时变的双选信道下,会受到由于多普勒影响引起的载波间的干扰的影响,为此文献[26]提出了将部分FFT解调应用到混合载波系统中,性能有了很大的提高,但是复杂度很高,在实际应用中会受到限制。文献[27]进一步将基于带状最小均方误差的信道补偿技术应用到混合载波在部分FFT解调下的系统中。
图6为对接收到的长时域序列进行4个部分的部分快速傅里叶变换(PFFT)解调过程的原理图。每个长序列经过补零后做点的FFT,再对各个部分分别做频域的信道抵消处理(如幅度和相位补偿)后合并,并输出频域估计序列。部分FFT被应用于多普勒影响较为严重的水下声纳信道或存在载波频偏的信道环境下时,可有效提高OFDM系统的性能,且随着时域序列划分区间个数的增加,系统误码性能越好。图7描述了WFRFT混合载波-部分FFT解调系统的设计思路[25]。
4 WFRFT抗截获
从信号波形的角度考虑,信号波形越复杂,则分选和识别的难度越大。文献[5]、[9-10]最初利用了WFRFT信号波形复杂、可控的特点,提出WFRFT在低截获、低检测通信中应用的可行性。针对低检测性能的评估,可以从两个层次进行。
(1)假设非目的接收机已知系统采用WFRFT技术的前提下,通过枚举检测识别WFRFT的参数。文献[5]、[9-10]分析了这种情况下WFRFT参数误差对于接收机解调误码率的影响,并简要分析了这种检测方式所需要付出的复杂度代价。
(2)当非目的接收机未知系统采用WFRFT技术而使用一些盲信号检测和调制识别手段时,一些常用技術手段对于WFRFT信号的识别效果。其中,基于高阶累积量、高阶循环累积量的方法是目前研究较多,理论相对完善,方法相对成熟的一种盲信号检测和调制识别手段。由于高斯信号的高阶累积量和高阶循环累积量恒为零,所以高阶累积量和高阶循环累积量的检测方法对于高斯信号而言是无效的或“盲”的,因此这两种方法即不受高斯噪声的影响又无法适用于类高斯噪声信号的检测。
此外,WFRFT对于通信信号的高斯化程度使得通信信号呈现出类高斯的统计特性,所以选取基于高阶累积量或高阶循环累积量或其两种融合的方式作为定量分析的特征,并在采用相同的调制方式识别器或级联分类器或并联分类器的情况下原有的调制识别方法失效。文献[29]对WFRFT信号高阶累积量特性进行了简要分析。此外,利用WFRFT信号的类高斯特性,文献[5]中设计了一种利用WFRFT信号进行波形搭载隐蔽通信的技术方案并将WFRFT与变换域通信系统(TDCS)结合用于卫星隐蔽通信中。
为了进一步保护WFRFT参数不被检测,文献[30]提出了WFRFT变参数通信方法,而多层变换[31]、并行组合扩[32]以及协作通信[33]等方案则进一步提升了WFRFT的抗截获性能。
5 结束语
文章中我们简要回顾了WFRFT被引入通信系统的发展历程,以及在混合载波通信、低截获/低检测概率通信等两个应用方面的主要研究成果。目前相关研究工作正继续遵循这两条主线渐次展开。随着5G移动通信网络和相关技术研究逐渐成为热点,包括一些单、多载波混合技术方案在内的许多新想法被提出,这些技术与WFRFT的关系与相关性、兼容性等问题都是值得深入研究的。更多样、广泛的信号检测、识别手段,也将应用于对WFRFT的检测与识别特性的评估方面。此外,随着WFRFT系统向实用化方向的推进,包括同步、信道估计等工程问题也是不可回避的。
参考文献
[1] SHIH C C. Fractionalization of Fourier Transform [J]. Optics Communications, 1995(5-6):495-498. DOI: 10-1016/0030-4018(95)00268-D
[2] LIU S, ZHANG J, ZHANG Y. Properties of the Fractionalization of a Fourier Transform [J]. Optics Communications, 1997(133): 50-54. DOI: 10.1016/S0030-4018(96)00478-6
[3] YEUNG D S, RAN Q, TSANG E C, et al. Complete Way to Fractionalize Fourier Transform [J]. Optics Communications, 2004, 230: 55-57. DOI: 10.1016/j.optcom.2003.11.054
[4] RAN Q, YEUNG D S, TSANG E C C, et al. General Multifractional Fourier Transform Method Based on the Generalized Permutation Matrix Group [J]. IEEE Transactions on Signal Processing, 2005, 53(1): 83-98. DOI: 10.1109/TSP.2004.837397
[5] 梅林. 加权类分数傅立叶变换及其在通信系统中的应用 [D]. 哈尔滨: 哈尔滨工业大学, 2010
[6] MEI L, ZHANG Q, SHA X, et al. WFRFT Precoding for Narrowband Interference Suppression in DFT-Based Block Transmission Systems [J]. IEEE Communications Letters, 2013, 17(10):1916-1919. DOI:10.1007/s11432-008-0073-6
[7] WEINSTEIN S, EBERT P. Data Transmission by Frequency-division Multiplexing Using the
Discrete Fourier Transform [J]. IEEE Transactions on Communication Technology, 1971, 19(5): 628-634
[8] MEI L, SHA X, ZHANG N. The Approach to Carrier Scheme Convergence Based on 4-Weighted Fractional Fourier Transform [J]. IEEE Communications Letters, 2010, 14(6): 503-505. DOI:10.1109/LCOMM.2010.06.092413
[9] 梅林, 沙学军, 冉启文, 等. 四项加权分数Fourier变换在通信系统中的应用研究 [J]. 中国科学: 信息科学. 2010, 40(5): 732-741
[10] MEI L, SHA X, RAN Q, et al. Research on the Application of 4-WFRFT in Communication System [J]. Science of China: Information Sciences. 2010, 53(6): 1251-1260
[11] WANG X, MEI L, WANG Z, et al. On the Probability Density Function of the Real and Imaginary Parts in WFRFT Signals [J]. China Communications, 2016, 13(9): 44-52. DOI: 10.1109/CC.2016.7582295
[12] MEI L, SHA X, ZHANG N. PAPR of Hybrid Carrier Scheme based on Weighted-type Fractional Fourier Transform [C]// 6th International ICST Conference on Communications and Networking in China (CHINACOM 2011). USA: IEEE, 2011:237-240
[13] WANG X, MEI L, ZHANG N, et al. PAPR Approximation of Continuous-Time WFRFT Signals [C]//2014 IEEE International Conference on Communication Systems (ICCS). USA: IEEE, 2014: 237-240. DOI:10.1109/ChinaCom.2011.6158155
[14] HUI Y, LI B, ZHANG T. 4-Weighted Fractional Fourier Transform over Doubly Selective Channels and Optimal Order selecting Algorithm [J]. Electronics Letters, 2015 , 51 (2) : 177-179
[15] 程曉霞, 陈相宁, 于爽, 等. 基于WFRFT的抗衰落通信系统性能研究[J]. 电子测量技术, 2015, 38(11): 143-147
[16] 邱昕. 基于分数傅立叶变换的混合载波通信系统性能研究 [D]. 哈尔滨: 哈尔滨工业大学, 2013
[17] 王. 基于加权分数傅立叶变换的双选信道下干扰抑制方法研究[D]. 哈尔滨:哈尔滨工业大学,2014
[18] MEI L, SHA X, ZHANG Q, et al. The Concepts of Hybrid-Carrier Scheme Communication System [C]// 6th International ICST Conference on Communications and Networking. USA:IEEE, 2011. DOI:10.1109/ChinaCom.2011.6158114
[19] QIU X, SHA X, MEI L. Performance of Hybrid Carrier DS-CDMA Communication System [C]// Communications and Networking in China (CHINACOM), 2011 6th International ICST Conference on. USA:IEEE, 2011. DOI: 10.1109/ChinaCom.2011.6158143
[20] QIU X, SHA X, MEI L. Hybrid Carrier Spread Spectrum System Based on 4-Weighted Fractional Fourier Transform [J]. China Communications, 2012, 9(1): 13-19
[21] WANG K, SHA X, MEI L, et al. Performance Analysis of Hybrid Carrier System with MMSE Equalization over Doubly-Dispersive Channels [J]. IEEE Communications Letters, 2012, 16(7): 1048-1051. DOI: 10.1109/LCOMM.2012.050112.120414
[22] WANG K, SHA X, MEI L. On Interference Suppression in Doubly-Dispersive Channels with Hybrid Single-Multi Carrier Modulation and an MMSE Iterative Equalizer [J]. IEEE Wireless Communications letters, 2012, 1(5): 504-507. DOI: 10.1109/WCL.2012.071612.120359
[23] WANG K, SHA X, LI Y. Hybrid Carrier Modulation with Time-Domain Windows and Iterative Equalization over Underwater Acoustic Channels [J]. IEEE Communications Letters, 2013 , 17 (8) : 1489-1492. DOI: 10.1109/LCOMM.2013.070913.130744
[24] WANG K, SHA X, LI Y. Iterative frequency-domain equalization for WFRFT and EST Based Modulation Schemes over Doubly Selective Wireless Fading Channels [C]// 2013 IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC). USA:IEEE,2013. DOI:10.1109/PIMRC.2013.6666371
[25] 李勇. 快速時变信道下基于WFRFT和部分FFT的传输方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2015
[26] LI Y, SHA X ,WANG K. Hybrid Carrier Communication with Partial FFT Demodulation over Underwater Acoustic Channels [J]. IEEE Communications Letters, 2013 , 17 (12) : 2260-2263. DOI: 10.1109/LCOMM.2013.102613.131651
[27] LI Y, SHA X, ZHENG F C, et al. Low Complexity Equalization of HCM Systems with DPFFT Demodulation over Doubly-Selective Channels [J]. IEEE Signal Processing Letters, 2014 , 21 (7) : 862-865.DOI: 10.1109/LSP.2014.2311128
[28] YERRAMALLI S, STOJANOVIC M, MITRA U. Partial FFT Demodulation: A Dection Method for Highly Doppler Distorted OFDM Systems [J]. IEEE Transformation Signal Process, 2012, 60(11): 5906-5918. DOI: 10.1109/TSP.2012.2210547
[29] FENG H, MEI L, SHA X, et al. Modulation Recognition for Hybrid Carrier Scheme Based on Weighted-type Fractional Fourier Transform [C]//6th International ICST Conference on Communications and Networking in China (CHINACOM 2011). USA: IEEE, 2011
[30] DING B, MEI L, SHA X. Secure Communication System Based on Alterable-Parameter 4-Weighted Fractional Fourier Transform [J]. Information Technology Journal, 2010, 9(1): 158-163.
[31] LI T, MEI L, WU X, et al. Anti-Interception Communication System Based on Double Layers Weighted-type Fractional Fourier Transform [C]// 6th International ICST Conference on Communications and Networking in China (CHINACOM 2011). USA:IEEE, 2010. DOI:10.1109/ChinaCom.2011.6158125
[32] FANG X, SHA , LI Y. Secret Communication Using Parallel Combinatory Spreading WFRFT [J]. IEEE Communications Letters, 2015 , 19 (1) : 62-65. DOI: 10.1109/LCOMM.2014.2359200
[33] FANG X, SHA X, MEI L. Guaranteeing Wireless Communication Secrecy Via a WFRFT-Based Cooperative System [J]. China Communications, 2015, 12(9): 76-82. DOI: 10.1109/CC.2015.7275261

