基于小波树和非局部TV的压缩感知MR图像重建
郝王丽+韩猛+胡欣宇


摘 要:核磁成像是一种非侵入式观测病人组织改变的技术,但其速度很慢,因此提高核磁图像的重建速度有着非常重要的意义。压缩感知常用来快速重建核磁图像,且被建模成一个包含数据保真项、稀疏先验项和全变分项的线性组合最小化问题。压缩感知理论表明,图像本身或其在某个变换域内越稀疏,其重建质量就越好。根据结构稀疏理论,一个长度为n的标准K-稀疏数据,若其是树稀疏的,用于重构的采样样本可由O(K+Klogn)减少到O(K+logn)。若经小波树变换后的图像是树稀疏的,便可获得更好的重建图像。全变分项虽然在复原图像结构方面很有效,但其会造成图像的过平滑并为重构图像带来块效应,非局部全变分可以克服其缺陷,并在保持图像边缘和细节信息以及提高信噪比方面很有优势。鉴于此,文中提出了基于小波树稀疏和非局部全变分的压缩感知核磁圖像重建模型。实验结果表明,利用该模型核磁图像可以很快地被重建且其图像细节信息得到了很好的保持。基于小波树稀疏和非局部全变分的压缩感知核磁图像重建模型在核磁图像重建质量和重构时间方面具有良好性能。
关键词:小波树;非局部全变分;压缩感知;核磁共振图像;图像重建
中图分类号:TP301.6 文献标识码:A 文章编号:2095-1302(2017)06-00-03
0 引 言
压缩感知理论领域的研究表明[1],从高度欠采样的k-空间数据中准确重构出核磁图像是可行的,且可以大大缩短核磁图像的扫描时间[2]。Lusting 等人首先将压缩感知理论应用到核磁图像的重建上[2],他们将核磁图像重建建模成如下优化问题:
其中,x为原始图像,b为欠采样k-空间观测到的数据,R为局部傅里叶变换,Φ为小波变换,α和β为两个正参数,用来协调两个约束项的关系。事实表明,小波变换和全变分可以稀疏地表示分段光滑的图像或组织。全变分项通常表示为,和分别表示图像在两个坐标方向上的前向有限差分操作,这种全变分也被称作局部全变分。
文献[2]中采用公式(1)组合小波稀疏和全变分(TV)两个先验约束项,求解压缩感知核磁图像重建问题,且实验表明,在欠采样率约为20%的情况下能获得较好的重建图像[2]。但图像在小波变换域内并不足够稀疏,且全变分很容易造成图像过平滑并引起块效应。为进一步提高图像表示的稀疏性,文献[3]中引入了稀疏性更好的小波树来替换(1)中的小波项,但并未解决全变分带来的图像过平滑以及块效应问题。为克服TV的内在缺陷,非局部全变分(NLTV)作为可以保护图像边缘及细节信息的约束项被引入核磁图像的重建[4]和图像去模糊的求解中[5],获得了很好的实验性能。但在文献[4]中,其稀疏约束项仍然采用小波变换。为了更好地保持图像边缘和细节信息,并进一步提高图像重建质量,本文提出基于小波树和非局部全变分的压缩感知核磁图像重建。
1 相关工作
1.1 基于树的压缩感知
如果一个信号是稀疏的或者能够被稀疏地表示,用于重建该信号所需采样的个数比奈奎斯特定理所需采样的个数少很多。而且若知道原始信号结构的一些先验知识,比如群或图结构,采样数目可以进一步降低[6,7]。一些算法就是利用小波系数的树机构来提高压缩感知重建效果[8-11]。OGL便用一个凸方法来建模树结构[8]:
其中,θ为小波系数集,A代表局部傅里叶变换,b为采样数据。ΦT代表逆小波变换,G代表所有的父亲-孩子组,g为G的一个组,为θ的扩展向量,最后一项是保证数据一致性的惩罚项。当小波系数恢复后,通过逆小波变换可重构图像。
1.2 非局部全变分
在文献[12-17]中,非局部全变分通过在正则化项中采用非局部像素计算梯度来解决全变分所带来的块效应问题,非局部全变分正则化项定义如下:
px(u) 和px(v)分别表示以点u和v为中心的图像块,权重函数用来度量图像块px(u) 和px(v)之间的相似度,Zx为标准化因子, σ为尺度参数,用来控制两图像块px(u) 和px(v)间的相似度。
2 问题模型及其求解
2.1 问题模型
压缩感知重建问题在本文中的建模如下:
为有效求解这个问题,引入变量y来约束有重叠结构的变量x, 使式(6)变为非重叠的凸优化问题。令GΦx=y,则式(6)可被重写为:
公式(7)中,对于y-子问题,我们可通过分组软阈值方法求得闭合形式的解;对于x-子问题,我们可将第一项和最后一项二次惩罚项结合起来;其余项的形式类似FCSA[18], 因此可通过迭代方式有效求解。
2.2 问题求解
如上所述,式(7)中的y-子问题可被写为:
综上,基于小波树稀疏和NLTV的压缩感知核磁图像重建模型的求解分为两大步,即首先利用软阈值方法求解y-子问题,然后再利用FCSA求解x-子问题。
在实际应用中,与传统的TV相比,虽然NLTV正则化项因其权重的计算遍布整个图像域,时间开销大,但它可通过很少的迭代次数获得很好的重建图像[5]。因此在保证重建图像质量的前提下我们采用文献[5]中周期性的更新NLTV正则化项的方法来缩短算法的执行时间。
现给出模型(6)的求解算法,为表示方便,我们将其简记为NLTV-WaTMRI。
公式(12)是将图像的像素值规范化到[l,u]范围内,且u>l≥0,若不执行该操作,则重建图像由于存在负数像素数值而出现伪影。T表示非局部全变分项的更新周期。
3 实验
为验证所提出模型的良好性能,我们将求解算法NLTV-WaTMRI与约束项为TV和小波树的WaTMRI[3]以及约束项为NLTV和小波的NLTV-FCSA[5]进行比较。因WaTMRI和NLTV-FCSA性能都比约束项为TV和小波的FCSA好[18],故此处FCSA不参与比较。公平起见,所有的算法都在Lenovo PC E2323机器上的Matlab2009b环境中运行。
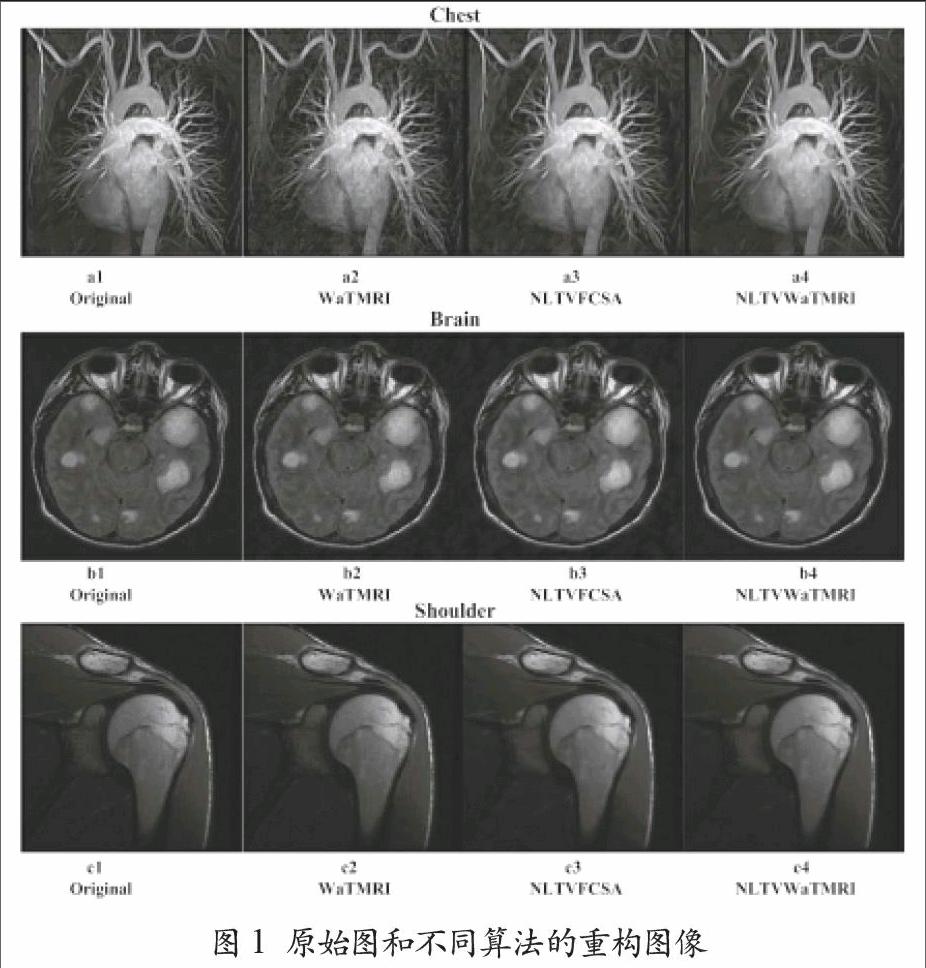
試验数据采用三幅常用的核磁图像Chest、Brain、Shoulder,如图1中的a1,b1,c1所示,均被规范化为256×256。设置欠采样率约为20%,稀疏约束都采用两级分解的Daubechies小波,正则化参数α,β设为0.001和0.035,λ=0.2β,最大迭代次数设为50。为进行试验模拟,k-空间的观测数据b上添加标准差为0.01的高斯白噪声。
图1显示了原始图像和利用不同方法重构的图像,由图可见,与基于NLTV的两种方法NLTVFCSA和NLTVWaTMRI相比,利用基于TV的WaTMRI方法重构图像的噪声比较大,且图像的边缘和细节信息不够清楚。这说明NLTV在抑制噪声和保持图像边缘细节方面比TV好。与基于小波稀疏的NLTVFCSA相比,基于小波树稀疏的NLTVWaTMRI重构图像要更清晰一些,说明图像在小波树变换域内比在小波变换域内更稀疏。
图2展示了三幅核磁图像利用不同重建算法的性能比较,第一排显示了不同重建算法在不同核磁图像上的信噪比(SNR)与迭代次数(Iterations)的关系,第二排显示了信噪比(SNR)与重建时间(CPU Time)的关系。由图2第一排可见,利用NLTVWaTMRI重建的图像有比其他方法更高的SNR,尤其比WaTMRI的高。根据图2中的第二排可知,NLTVWaTMRI的时间性能比NLTVFCSA好,比WaTMRI略差,但却有比WaTMRI高的多的SNR。
综上所述,在重建时间相当的情况下,本文所提模型的求解算法NLTVWaTMRI与其他算法相比,具有更好的图像边缘细节保持能力,可以获得更高的信噪比。
4 结 语
本文提出了基于小波树稀疏和非局部全变分的压缩感知核磁图像重建模型。小波树变换有比小波变换更好的稀疏性,故其重建图像质量更好。NLTV不仅可以避免由TV引起的图像过平滑及块效应问题,还能更好地保持图像边缘和细节信息,抑制噪声,故其重建图像边缘细节更清楚且噪声更小。虽然NLTV权值的计算很耗时,但我们只执行很少次数的权值更新,故重建时间不长。
参考文献
[1] Donoho D. Compressed sensing[J].IEEE Transactions on Information Theory, 2006, 52(4): 1289–1306.
[2] Lustig M, Donoho DJ.Sparse MRI: The application of compressed sensing for rapid MR imaging[J].Journal of the Chemical Fertilizer Industry,2007,58(6):1182-1195.
[3] Huang J,Yang F.Compressed magnetic resonance imaging based on wavelet sparsity and nonlocal total Variation[J].2012 IEEE 9th International Symposium on Biomedical Imaging, 2012,5(1):968-971.
[4] Liang D,Wang H,Chang Y,et al.Sensitivity Encoding Reconstruction With Nonlocal Total Variation Regularization[J].Magnetic Resonance in Medicine official journal, 2011,65(5):1384-1392.
[5] Chen C, Junzhou H.Compressive Sensing MRI with Wavelet Tree Sparsity[C].In Proc. of the 26th Annual Conference on Neural Information Processing Systems (NIPS), 2012,evada, USA, December.
[6] Huang J,Zhang T,Metaxas D.LearningWith Structured Sparsity[J].Journal of Machine Learning Research,2009,12(7):417-424.
[7] Baraniuk R G, Cevher V, Duarte M F, et al.Model-based compressive sensing[J].IEEE Trans on Information Theory,2010, 56(4):1982-2001.
[8] Rao N, Nowak R, Wright S, et al.Convex approaches to model wavelet sparsity patterns[C].In IEEE International Conference On Image Processing, 2011, ICIP11.
[9] He L, Carin L.Exploiting Structure in Wavelet-Based Bayesian Compressive Sensing[J].IEEE Trans. on Signal Processing, 2009, 57(9):3488-3497.
[10] He L, Chen H, Carin L.Tree-Structured Compressive Sensing with Variational Bayesian Analysis[J].IEEE Signal Processing Letters,2009,17(3):233-236.
[11] Som S, Potter L C, Schniter P.Compressive Imaging using Approximate Message Passing and a Markov-Tree Prior[C].In Proceedings of Asilomar Conference on Signals, Systems, and Computers,2010,
[12] Zhang X, Burger M, Bresson X X, et al.Bregmanized nonlocal regularization for deconvolution and sparse reconstruction[J].SIAM Journal of Image Science, 2010,3(3):253-276.
[13] Peyre G, Bougleux S, Cohen L. Non-local regularization of inverse problems[C].in Proceedings of ECCV, 2008.
[14] Mignotte M. A non-local regularization strategy for image deconvolution[J].Pattern Recognition Letter,2008,29(16):2206-2212.
[15] Elmoataz A, Lezoray O, Bougleux S.Nonlocal discrete regularization on weighted graphs: a framework for image and manifold processing[J].IEEE Transaction on Image Processing,2008,17(7):1047-1060.
[16] Lou Y, Zhang X, Osher S,et al.Image recovery via nonlocal operators[J].Journal of Scientific Computing,2010,42(2):185-197.
[17] Gilboa G, Osher S. Nonlocal operators with applications to image processing[J].Multiscale Model Simulation,2008,7(3):1005-1028.
[18] Huang J, Zhang S, Metaxas D.Efficient MR image reconstruction for compressed MR imaging[J].Med. Image Anal, 2011, 15(5):670-679.

