基于自适应场景系数的室内三维定位模型

许 万， 沈伟刚

(湖北工业大学机械工程学院 ， 湖北 武汉 430068)

基于自适应场景系数的室内三维定位模型

许 万， 沈伟刚

(湖北工业大学机械工程学院 ， 湖北 武汉 430068)

基于无线通信基站的室内三维定位的最小二乘迭代模型经常出现迭代发散的问题，从而导致定位失败,通过对比由该模型计算的迭代初值与终端坐标准确值，推断失败原因是由于迭代初值误差过大导致后续迭代发散。提出基于自适应场景系数的室内三维定位模型，使用改进后的模型再次分析试验数据，求解的初始值与迭代值都非常接近准确值。最后通过误差分析，该模型的定位精度可达0.5 m，场景内的相对误差小于0.2%。

室内三维定位； 自适应场景系数； 最小二乘法； 迭代发散

随着无线通信网络和移动互联网的快速发展，提供基于地理位置信息的精确定位服务已经成为信息领域的研究热点之一。目前，商用GPS随着智能手机的发展已经得到了广泛的应用。但是，在诸如室内、地下、高楼林立的市区等障碍物密集的区域，GPS的定位性能较差。在此条件下，基于无线网络基站的定位系统相比GPS存在较大的优势。同时，与通过WIFI设备与手机进行通信相比，手机基站的覆盖范围相对较广。可以通过测量无线电信号在终端到基站之间的时间(TOA)来计算终端的位置，但是大多数情况下测量的TOA数据包含测量误差和系统误差，而且非视距传播(NLOS)对TOA的影响更为显著，所以在测量误差和系统误差不可避免的前提下，如何将LOS和NLOS混合的TOA数据统一，成为精确计算终端位置的关键。

Chan[1]在TOA基础上使用两次加权最小二乘法，对移动终端位置进行了确定。华惊宇[2]采用二次规划的方法，将NLOS误差问题转换成二次规划的问题，然后对目标函数求极值来减少NLOS误差的影响。陈长衍[3]利用散射模型中LOS/NLOS传播的统计特征进行NLOS误差的减弱。崔玮[4]通过数据进行训练W确定高斯混合模型对距离的最佳估计参数来减弱NLOS误差。Wylie M P[5]使用LOS重构，先对测量样本进行平滑，然后通过平移平滑后的曲线进行LOS重构。本文在上述研究的基础上，通过设置自适应场景系数K，将LOS或NLOS的TOA测量数据转化成统一的依赖于环境的TOA数据，然后利用转换后的TOA数据，使用最小二乘法计算初始终端位置，将其作为迭代初始值代入迭代误差模型中，计算出满足收敛条件的终端位置值。使用该方法确定终端的位置，只需要在计算第一个终端的位置坐标时通过给定的方法计算出自适应场景系数即可，再去计算该区域内其他终端的位置时可继续使用该场景系数，即对于固定的场景(基站数目与位置固定)，所有终端共享同一个自适应场景系数。所以在实际应用中，可以在安装基站时就将场景系数测算出来，大大提高了终端定位速度。

1 最小二乘定位模型

根据测量得到的未知终端的TOA，计算无线电信号传播的距离，将此距离作为TOA距离Rj：

Rj=cτj,j= 1, 2, 3, …N

(1)

其中：N为基站总数；c表示光速；τj代表原始TOA测量数据。若测量的TOA均为LOS环境下测量的值，且无误差，则Rj即可表示为终端到基站的真实距离。但是由于实际测量中的NLOS环境不可避免，即式(1)计算的终端位置十分不准确，所以用式(2)代替式(1)，表示终端到基站的位置，以便通过最小二乘法计算终端位置

(2)

式中：xj、yj、zj和x、y、z为第j个基站和终端的三维坐标。展开得

(3)

其中：

kj=(xj)2+(yj)2+(zj)2；

R2=x2+y2+z2

第一个基站到终端的距离平方与其他各个基站到该终端的距离平方之差

(4)

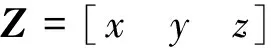
H=GZ

(5)

其中：

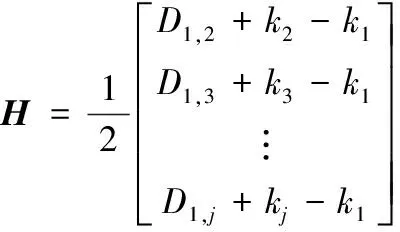
在编程计算时，D1,j中的Rj还是使用式(1)来计算。因为H和G均为N-1行矩阵，所以Z通常无法求出准确解。可以对式5利用最小二乘法求解其近似解，则有：

Z=(GTG)-1GTH

(6)

式(6)计算的Z仍然不够精确，需要进一步缩小终端位置的计算误差。以式(6)计算的坐标为初始参考点，建立该参考点的误差公式

(7)

式中：Rj表示第j个基站到移动终端实际距离。

应用泰勒级数展开进行迭代计算，并且忽略二阶以上分量，将误差转换成矩阵可得：

h=gδ+ξ

(8)

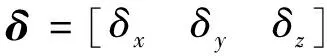
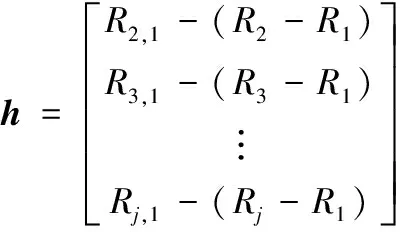
式(8)通常情况下无准确解，继续使用最小二乘估计求解，则有

δ=(gTg)-1gTh

(9)

在第k次迭代后，终端坐标(x,y,z)坐标变成

(10)

直至|δx|+|δy|+|δz|≤δM停止，其中δM表示最大允许误差。

2 基于自适应场景系数的室内三维定位模型

2.1 模型的建立

在实际求解中，往往会发现上述迭代求解的计算结果会有复数，这就说明其经典三维定位模型不稳定，无法适应于情况较复杂的场景。通过试验，比较实际终端位置(或与基站的距离)与上述经典方法计算的终端位置，可以得出迭代计算结果并不准确的结论。在某次试验中，在一个场景内设定30个基站，基站位置随机分布，然后实验人员手持终端在场景中移动，记录不同位置时的TOA数据，然后使用上面的经典三维定位模型进行定位计算。基站位置与终端位置如图1所示。

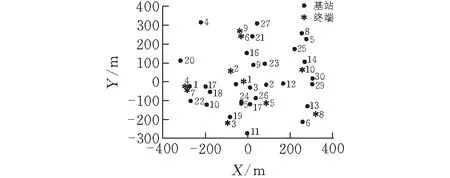
图 1 基站与终端位置

通过计算，发现经典算法的迭代很容易发散，从而导致定位失败。该试验中10个终端的TOA数据经过经典算法计算的初始值如表1所示。

因为在试验中终端相对地面的高度几乎不变，所以在计算时就忽略纵轴，而只是对终端位置进行平面定位。表1中还给出了各个终端位置的准确值。通过分析初始值的横纵坐标，发现两者的差异很大，所以猜测经典算法后续迭代经常发散的原因可能是初始值的计算偏差很大。初始值的计算依赖于D1,j，而D1,j取决于Rj。在实际计算时的Rj值是由TOA数据转换成距离直接计算的，该值带有很大的误差。进一步发现，R与Rj的比值又在常数0.5左右波动，所以对Rj进行线性放缩小，然后再代入式5中计算矩阵H。则式(1)可改进为

Rj=K·cτj

(11)

式中：K即为自适应场景系数。

改进后的模型称为基于自适应场景系数的三维定位模型。

表1 最小二乘定位模型计算结果

2.2 自适应场景系数K值的确定

场景系数K是跟测量TOA的环境有关的系数，通常认为环境中的NLOS越多，无线电传播过程中反射或折射次数越多，K值越小；NLOS越少，无线电传播过程中反射或折射次数越少，K值越接近于1。在初步定位估计中需要使用场景系数将TOA数据转化成环境TOA，所以需要确定场景系数K。由于测量TOA必然大于实际的TOA，所以场景系数必定小于1。将不同的K值计算的Rj代入上述误差迭代修整模型中进行计算，迭代收敛或发散均有发生。所以，确定场景系数K的方法为：K从1开始，以0.01为步长递减，以迭代收敛为终止搜索条件，计算场景系数K的初始值。此时已经计算出一个终端坐标值，计算该值到第一个基站的距离并将其作为计算距离。用计算距离除以给出的同一个终端到第一个基站的测量TOA计算的测量距离，即可得到最终的场景系数K。再利用计算的最终场景系数，代入模型求解，即可得到更为

精确的终端三维坐标。

3 模型验证

利用之前试验的数据(基站位置和终端到基站的TOA)，经过基于自适应场景系数的三维定位模型的计算，忽略终端高度方向的坐标，其迭代求解出的终端位置与准确位置如图2所示(其中场景系数K的计算值为0.705)：

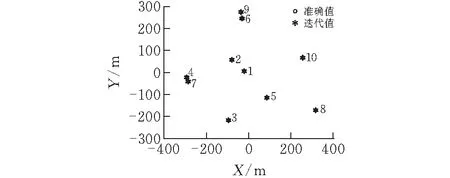
图 2 改进模型计算的终端位置

从图2可见，使用基于自适应场景系数的三维定位模型计算的终端位置坐标与准确值几乎重合，具体的坐标值如表2所示。

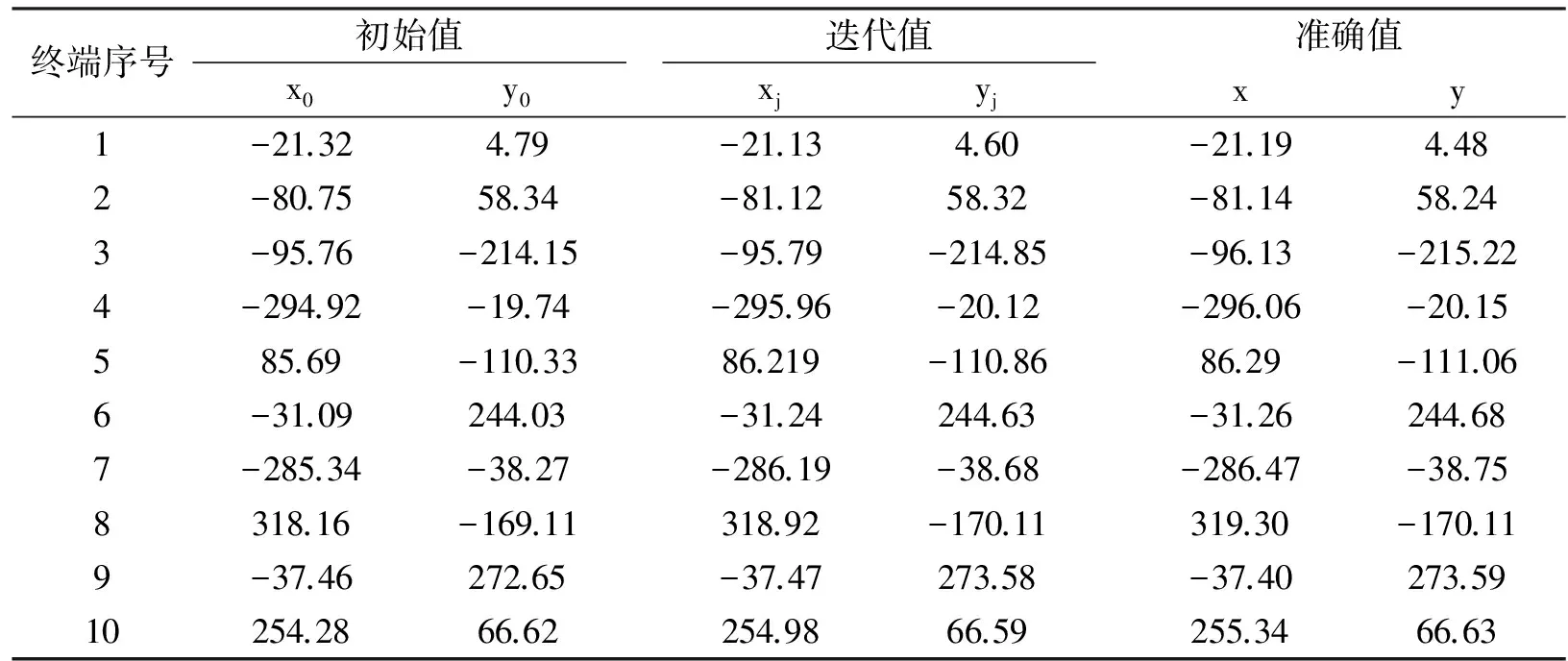
表2 改进模型计算的终端坐标值 m

表2中的初始值表示使用基于自适应场景系数的三维定位模型后计算的迭代初始值，表中的迭代值表示使用初始值迭代后更精确的终端坐标。分析表2中数据可知，改进后的模型计算初始值就已经很接近终端的准确值，这也说明基于自适应场景系数的三维定位模型具有很高的定位精度。

进一步对表2所示数据进行误差分析，模型误差

(12)

计算终端坐标的相对误差

(13)

将数据代入式(12)、(13)中，计算该模型的误差如图3所示，相对误差如图4所示。

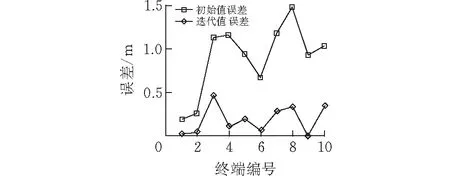
图 3 改进模型求解误差

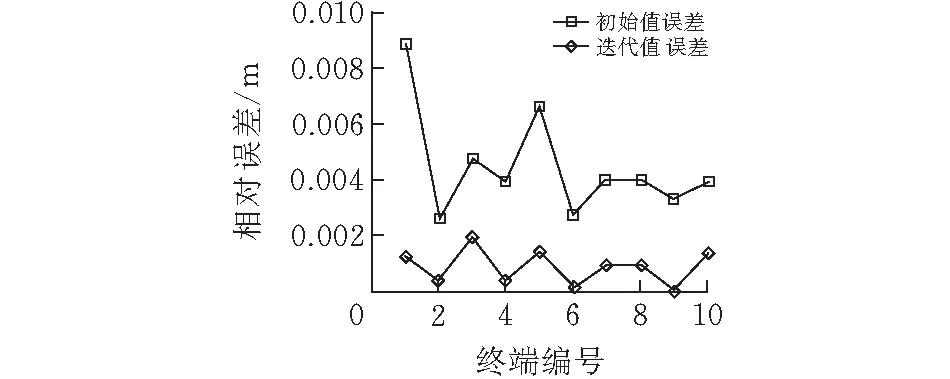
图 4 改进模型求解相对误差

从图3中可知，使用该模型计算的初始值误差小于1.5 m，迭代值误差小于0.5 m，足以说明该模型具有很高的精度。图4中所示的初始值相对误差小于1%，迭代值相对误差小于0.2%也能说明该模型精度很高。

4 结论

1) 通过建立基于自适应场景系数的三维定位模型，很好地克服经典三维定位模型存在的求解精度不高、迭代容易发散的弊端。该模型相对于经典模型的改进很小，但效果却很显著，具有很好的适用性。

2) 使用恒定步长方法搜索计算自适应场景系数，方法简单实用。但是以迭代收敛为搜索终止条件使得自适应场景系数的计算需要一定时间，从而在实际应用中无法做到快速计算。试验发现，通过第一个终端计算的场景系数同样适用于其他终端，说明自适应场景系数与终端的位置无关(研究发现，自适应场景系数与基站位置与数目有关)。所以在实际使用中，事先计算好每一个场景的自适应系数，即可实现快速定位。

3) 通过试验，将基于自适应场景系数的三维定位模型计算的终端位置迭代值与准确值进行对比，得出该模型的定位误差小于0.5 m，相对误差小于0.2%，足以说明该模型的定位精度很高。

[1] Chan Y T, Ho K C. A simple and efficient estimator for hyperbolic location[J]. Signal Processing IEEE Transactions on, 1994, 42(8):1905-1915.

[2] 华惊宇, 郑志龙, 周凯,等. NLOS无线环境中运用最优化原理的定位算法[J]. 浙江工业大学学报, 2014, 42(1):93-98.

[3] 屈保平, 袭著有, 陈长衍. 一种NLOS环境下基于散射模型的TOA定位方法[J]. 火力与指挥控制, 2014(5):27-30.

[4] 崔玮, 吴成东, 张云洲,等. 基于高斯混合模型的非视距定位算法[J]. 通信学报, 2014(1):99-106.

[5] Wylie M P, Holtzman J. The non-line of sight problem in mobile location estimation [C]// IEEE International Conference on Universal Personal Communications. 1996(2):827-831.

[6] 陆音, 王宝全, 丘觐玮. CHAN算法在LOS和NLOS环境下的定位研究[J]. 计算机技术与发展, 2015(9):61-65.

[7] 徐彤阳. NLOS环境下无线传感器网络TOA定位算法[J]. 计算机工程, 2013(12):93-96.

[8] 段凯宇, 张力军. 一种在NLOS环境下提高精度的TDOA定位方法[J]. 南京邮电大学学报(自然科学版), 2005, 25(5):15-19.

[责任编校： 张 众]

Three-Dimension Positioning Model Based on Adaptive Coefficient of Indoor Scene

XU Wan, SHEN Weigang

(SchoolofMechanicalEngin.,HubeiUniv.ofTech.，Wuhan430068，China)

To solve the indoor 3D location problem based on the wireless communication base station, the least square iteration model of Indoor 3D localization was established. Through the practical application, it has found that the problem of iterative divergence the model often arises, which could result in the failed positioning. Analysis of the iterative initial value calculated by this model and the terminal coordinate of the exact value, suggests that the subsequent iteration divergence has been caused by the large iterative initial value error, and then the 3D positioning model based on adaptive coefficient of indoor scene has been put forward. The improved model was used to analyze the test data again, and the initial values and the iteration values were very close to the exact values. And finally through error analysis, the positioning accuracy of the model is 0.5m, and the relative error of the model is less than 0.2%.

indoor 3D location; adaptive coefficient; least square method; iterative divergence

2017-03-02

许 万(1979-)， 男， 湖北武汉人，工学博士，湖北工业大学副教授，研究方向为机械控制方向

沈伟刚(1992-)，男，湖北襄阳人，湖北工业大学硕士研究生，研究方向为机械电子工程

1003-4684(2017)02-0012-04

TP301.6

A