外加驱动控制法在Buck变换器非线性现象控制中应用
房俊龙,靳惠雅,佟殿馨,和雪迪,杨敬然,刘鹏,张环宇
(东北农业大学电气与信息学院,哈尔滨150030)
外加驱动控制法在Buck变换器非线性现象控制中应用
房俊龙,靳惠雅,佟殿馨,和雪迪,杨敬然,刘鹏,张环宇
(东北农业大学电气与信息学院,哈尔滨150030)
针对电压模式控制Buck变换器运行时参数变化导致系统出现分岔和混沌等非线性现象问题,结合Buck变换器电路结构及其精确状态方程模型,运用Matlab/Simulink软件建立仿真模型并加驱动控制信号,通过控制信号幅值及相位调节,使系统达到最优非线性控制结果。仿真结果表明,当系统电路参数变化时,采用外加驱动控制法可有效抑制系统中非线性现象,系统稳定运行,通过搭建电压模式控制Buck变换器实验平台验证该方法对控制非线性现象具有可行性。
Buck变换器;仿真;外加驱动控制;非线性现象
DC-DC Buck变换器是典型非线性系统,具有响应快速、节能及抑制电网谐波电流等优点,在电控设备中应用广泛。由于变换器实际操作过程中经常出现不明噪声、电磁干扰、次谐波振荡等不规则现象,DC-DC变换器易发生非线性动力行为,导致系统运行紊乱、工作性能恶化等[1]。近年来,Buck变换器非线性系统中分岔与混沌现象成为电力电子技术领域研究热点之一。
目前,学者提出多种抑制非线性现象控制方法,如OGY方法[2]、延迟反馈控制方法[3]、自适应控制方法[4]、非线性控制方法[5]等。可有效控制变换器非线性现象,但延迟反馈控制法由于参数选择受限,调整时间较长,控制效果不理想;PID非线性控制方法,对输入信号不超过斜波补偿情况简单实用,但对复杂非线性系统和复杂信号追踪存在局限性[6]。复杂情况使用以上方法需一个已知周期目标轨道,难以控制到预知轨道上,效果不佳。多数研究停留在理论分析和仿真层面,DC-DC变换器分岔和混沌现象实际控制和应用受限。
本文以电压模式控制Buck变换器为例,对其变换器在Matlab/Simulink中仿真研究[7],在该模型基础上外加一个驱动信号作为控制信号,易产生周期信号,使系统处于稳定状态。该模型可精确调整参数,对系统操作稳定性设计具有指导意义[8]。搭建电压模式控制Buck变换器实验平台并对比分析试验仿真结果,为设计Buck变换器电路提供理论基础。
1 Buck变换器电路结构及数学模型
1.1 Buck变换器电路结构及其状态方程
电压模式控制Buck变换器是以电压为控制对象DC-DC变换器,基本电路拓扑结构如图1(a)所示。这是一种典型脉宽调制(PWM)控制系统[9]。图1(a)中G为开关器件;D为续流二极管;iL为电感L上流过电流;V0为输出电压(即电容电压VC),Vref为参考电压,在电压模式控制下,输出电压V0与参考电压Vref误差经放大器得到控制电压:

将这个控制电压信号与锯齿波信号比较,锯齿波信号Vramp定义为:
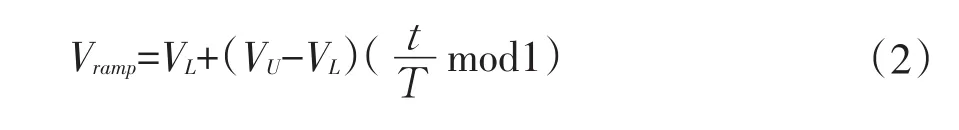
比较器输出用来控制开关脉宽调制信号u,控制开关G,即

当u=1时,开关G导通,则二极管D截止,输入电源E与电感L及RC输出部分串联,电感电流呈近乎线性上升;当u=0时,开关截止,则二极管D导通,电感电流通过二极管和负载呈近乎线性下降,控制波形如图1(b)所示。根据控制电压与锯齿波电压比较产生脉宽调制信号驱动开关G导通和截止。DC-DC变换器可分为两种工作模式:电流连续模式(在开关周期内电感电流iL>0)和电流不连续模式(在开关周期内电感电流iL<0)。本文仅分析Buck变换器工作于电流连续模式下情况[10],根据KCL和KVL定律及变换器工作拓扑结构,变换器状态方程如公式(4)所示:

其中设X为状态变量,X=[VC,iL]T,A和B是系数矩阵:
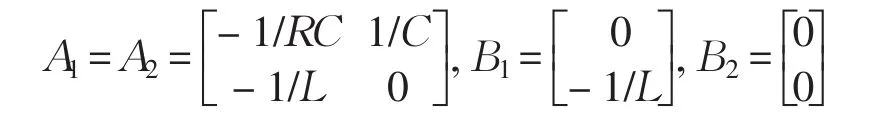
根据方程可以得到包含控制信号u统一方程如公式(5)所示:
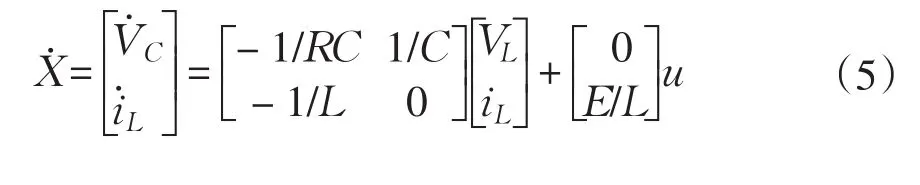
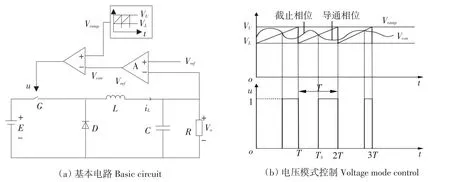
图1 电压模式控制Buck变换器Fig.1Voltage mode controlled Buck converter
1.2 电压模式Buck变换器离散迭代映射模型
由非齐次状态方程求解过程可见,在建立变换器闭环离散时间映射时,根据不同采样方式,分为频闪、同步切换、异步切换映射等。其中频闪映射在DC-DC变换器中是应用最为广泛闭环离散迭代映射[11]。频闪映射通过每个锯齿波周期开始时刻对变换器状态变量一次数据采样,利用数建立变换器数学模型。先确定初值,以该初值作为变量求解下一个周期解,反复迭代过程,最终得到符合要求精确解。因此DC-DC变换器动态情况实际是Xn和Xn+1间关系式:

其中Δt1=t1-tn为模态S1工作时间,Δt2=tn+1-t1= T-Δt1为模态S2工作时间。在研究Buck变换器系统时,通常将导通与关断视为两个独立系统,分析动力学特性及稳定性。当Buck变换器工作在关断状态时,状态轨迹在平衡点附近,如果某一时刻控制电压小于斜坡电压,则开关动作电路拓扑结构发生变化,Buck变换器转化至导通状态工作,当出现跳跃周期时,两个工作时间一个为锯齿波周期,另一个为0。当系统某一参数发生变化时,不稳定周期系统将会分岔至更高周期状态,以此类推,随着周期分岔变化,系统将由一系列周期轨道分岔直至混沌状态,寻找适合此类电路特点混沌控制方法。
2 Buck变换器非线性现象分析
2.1 仿真模型建立
根据公式(5)和图1(a)所示PWM控制方式建立电压控制型Buck变换器仿真模型如图2所示,选取电路参数为:E=23 V,L1=20 mH,R=22 Ω,C= 47 μF,A=8.4,Vref=11.3 V,VL=3.8 V,VU=8.2 V,T= 0.4 ms。对电压模式Buck变换器数值计算求解,并在Matlab软件中Simulink环境下构造分段光滑开关模型,采用龙格-库塔算法仿真,得到电压模式Buck变换器中电感电流和输出电压,控制电压信号和锯齿波信号从稳定、分岔到混沌变化时域分析,根据公式(7)电压模式Buck变换器精确离散迭代映射模型,在Matlab中M文件编写仿真程序得到该变换器电感电流和输出电压离散值。
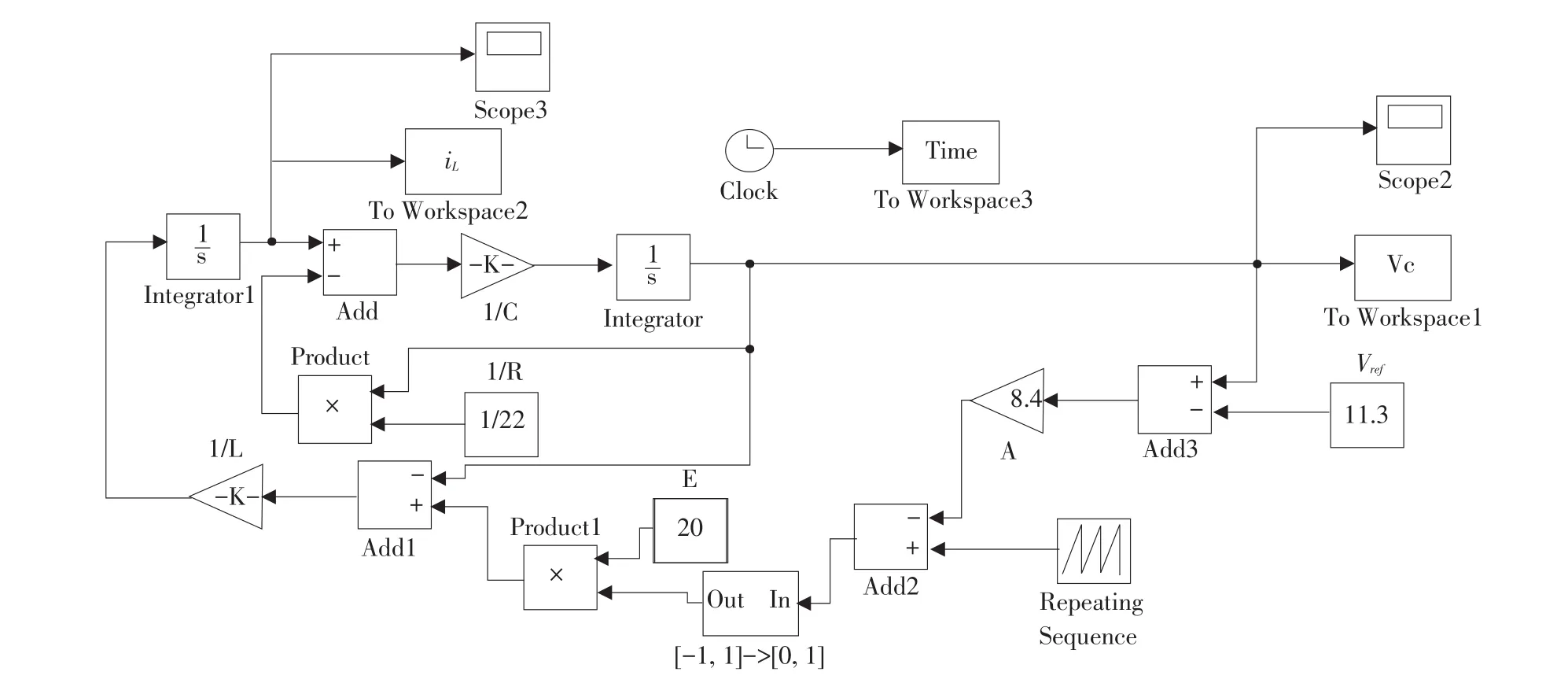
图2 电压控制型Buck变换器仿真模型Fig.2Simulation model of voltage controlled Buck converter
2.2 仿真结果与分析
在Buck变换器中,主要考虑以参考电压Vref为变化量,观察输出电压、电流分岔与混沌相图和时域波形、控制信号与锯齿波信号时域波形,如图3、4、5所示。
由仿真可知电压模式Buck变换器随参考电压Vref逐渐减小,相图中“洞”发生变化,洞口被倍周期分岔、混沌吸引子等规律填充。由图3可见,输出电压和电流相图由稳定状态经2倍周期分岔到紊乱混沌状态过程。当参考电压Vref=6 V时,系统发生首次倍周期分岔,出现2分裂极限环如图3(b)所示,比较图3(b)和图3(c)可知:参考电压Vref=4.5 V时,出现四分裂极限环,即四倍周期分岔。当参考电压Vref=3 V时,电路经历系列分岔,发生激变进入不稳定混沌状态吸引子越来越大,图3(d)所反映即吸引子尺寸增大相图[12]。
由图4可见,输出电压电流随参考电压不断减小而紊乱,进入混沌状态,成为类似随机过程;控制信号和锯齿波信号相交不具规律性,如图5(d)所示,在某些周期内控制信号和锯齿波信号无交点,出现周期跳跃。输出电流和电压在Vref=3 V时通过离散迭代映射取得离散值见图6,每一个采样点对应多个电压电流值,变换器工作紊乱,系统产生非线性现象。
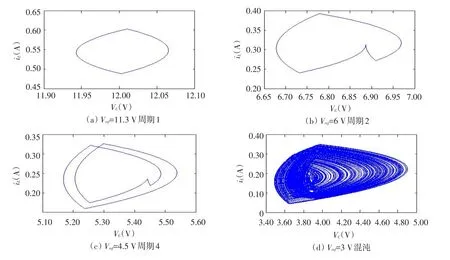
图3 Buck变换器电流-电压相Fig.3Current voltage phase of Buck converter


图4 Buck变换器输出电压与电流时域Fig.4Output voltage and current time domain of Buck converter
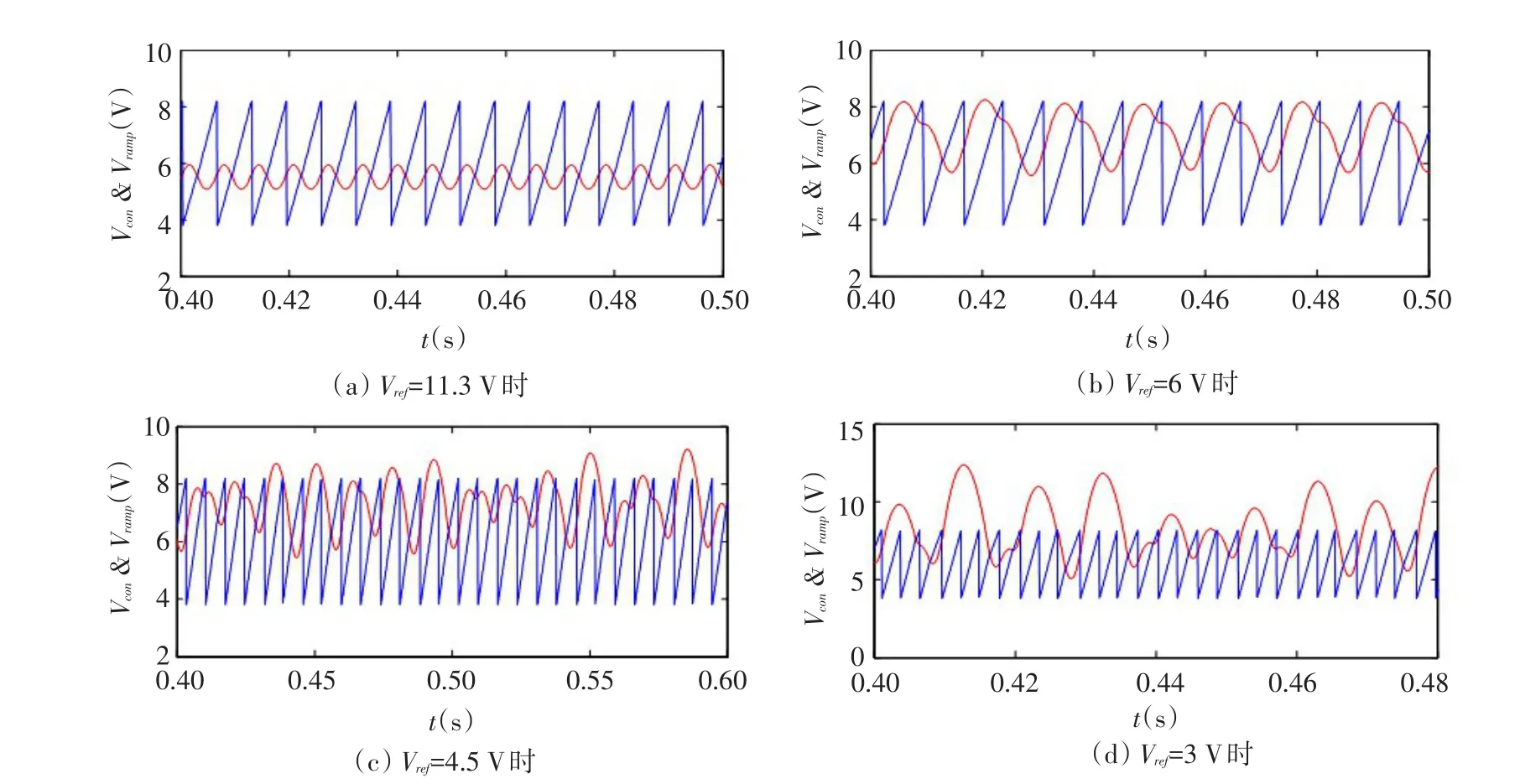
图5 控制信号与锯齿波信号Fig.5Control signal and the sawtooth wave signal
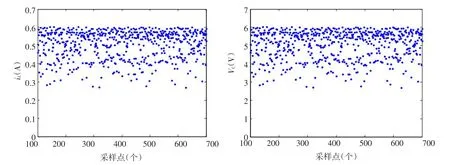
图6 输出电压与电流在混沌时离散值Fig.6Discrete values of output voltage and current in chaos
3 外加驱动控制法对系统稳定性影响
3.1 外加驱动控制法原理
外加驱动控制法是一种非反馈混沌控制方法,其控制机理是施加外部驱动控制信号后,系统从自身无限多不稳定极限环中找到与某个外加驱动信号共振极限环,使系统保持在稳定周期状态。基本特点是其控制信号不受系统变量实际变化影响,可完全避免对系统变量数据持续采集和响应,当混沌现象被控制后,系统实现状态通常不是非控制系统原有轨道,控制信号须保持非零值,方法简单且抗干扰性好,更适于实际操作。
系统外加驱动信号作为控制信号,一般是弱周期信号(即周期性脉冲信号或正弦信号)。在预先设定弱周期信号作用下,开环系统混沌轨道可移动相点使轨道成为闭环,使紊乱混沌运动变为稳定周期运动。对系统参数施加驱动特定频率、相位和幅度干扰,影响系统混沌动力行为。适当相位驱动干扰可使系统稳定在某一周期轨道上[13]。因此,在实际操作中选择对系统稳定性影响较大的易改变参数作激励参数。电压模式Buck变换器在可选择参考电压作激励参数,引入驱动控制信号A,把A用Asin(ωt+θ)代替,该驱动控制信号与变换器开关同频率,当改变正弦波幅值和相位时,可促使系统从混沌状态向周期状态过渡。
3.2 外加驱动控制法对系统稳定性影响分析
对激励参数施加一个微小正弦周期信号,控制电路中出现混沌现象。参考电压为:

αsin(2πfst+θ)为驱动控制信号:α为驱动控制信号强度,θ为驱动控制信号初相,其中fs为扰动频率(fs=f=1/T),构成共振驱动响应。根据已知电压模式Buck变换器随参考电压Vref变化相(见图3),当参考电压Vref=3 V时,变换器处于混沌状态。采用外加驱动控制电压模式Buck变换器中混沌现象,在Simulink中加入一个周期性脉冲或正弦信号,在某个节点里加一个信号源作控制源,设置延迟时间。驱动控制信号有两个可调节改变参数α和θ,为缩减参数范围,本文θ=0,对应不同α值观察电路采样[14]。混沌工作状态如图3(d)所示,控制结果如图7(a)所示,当α≥0.018时,系统受控稳定。在本研究中取较小驱动控制干扰强度作进一步分析,当α=0.018时,对应不同θ∈(0,2π)电路运行状态如图7(b)所示,可知θ≈2时,系统最稳定,使混沌运动稳定在周期1轨道上如图7(c)所示。
通过对图2所示Buck变换器仿真模型中参考电压施加一个驱动控制信号后,系统可在参考电压变化范围内稳定运行如图8所示,从输出电压、电流、控制信号和锯齿波信号仿真波形图可见,波形平滑有序,施加驱动控制后仿真结果与图4(d)和图5(d)比较,当Vref=3V时,系统处于混沌状态,加入一个周期信号后,电感电流iL在[0.16 A,0.5 A]范围内稳定运行,输出电压VC在[4.05 V,5 V]范围内稳定运行,系统不再出现周期跳跃,使Buck变换器规律性稳定在周期1状态。施加驱动控制后输出电流与电压离散值与图6结果相对,输出电压电流根据采样点选取,证明外加驱动控制法可有效抑制电压模式Buck变换器中分岔和混沌等非线性现象。
外加驱动控制法优势在于产生周期微扰信号,利用受控系统自身输出信号反馈控制[15],抑制或消除混沌现象使系统归于稳定有序状态,即将变换器混沌转为稳定周期状态。利用外加驱动控制法可降低电磁干扰,改善电路稳定性能,适于工程电力电子电路中控制实现。

图8 施加驱动控制后仿真波形Fig.8Simulation waveform after driving control
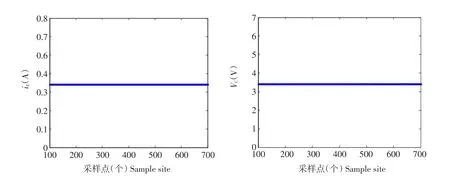
图9 施加驱动控制后输出电流与电压离散值Fig.9Discrete values of output current and voltage after driving control
4 试验验证及对比分析
4.1 试验方案设计
试验研究法是研究DC-DC变换器复杂动力学行为重要方法。数值仿真可直观理解复杂动力学行为,通过理论分析可解释发生复杂动力学行为原因。
Buck变换器电路非线性控制策略与方法主要有反馈控制方法、OGY方法、最优控制方法、脉冲控制方法等[16]。控制系统中分岔和混沌等非线性现象以及降低电磁干扰改善电磁兼容性等问题广受关注,本文在Buck变换器非线性控制基础上提出外加驱动控制方法,为验证该方法在理论分析过程中正确性以及试验可行性,搭建基于电压模式控制Buck变换器电路仿真试验平台,硬件电路所需模块装置(见图10),该试验装置中采用MOSFET作开关元件,其中PWM电压模式比较器采用SG3525芯片,该芯片工作在主从模式,可将输出驱动改为推拉输出形式,增加驱动能力,限制最大占空比。在试验过程中提供一个可访问反向输入和输出全补偿误差放大器,此放大器具有92dB典型直流电压增益特点,用于外部回路补偿。参考电压为工作时电容提供充电电流,参考部分具有短路保护功能并向附加控制电路供电,提供超过20 mA电流。在试验调试过程中,选取电路参数与数值模拟和仿真验证时系统参数一致,由实际运行条件下系统时域波形图可观察电路参数对系统性能影响,验证所选取混沌控制方式可行性和优越性。

图10 硬件电路所需模块装置Fig.10Hardware circuit required module device
4.2 试验仿真结果与对比分析
结合本文建立仿真模型及试验,利用外加驱动控制法分析电压模式Buck变换器因参数发生敏感变化而发生的一系列不稳定变化。经过大量数值仿真试验分析结果可知,当参考电压Vref=3V时,示波器输出电压电流波形结果(见图11、12),由波形结果可见,电路正常运行时,输出电压和电流出现从倍周期分岔再到混沌一系列不稳定变化。
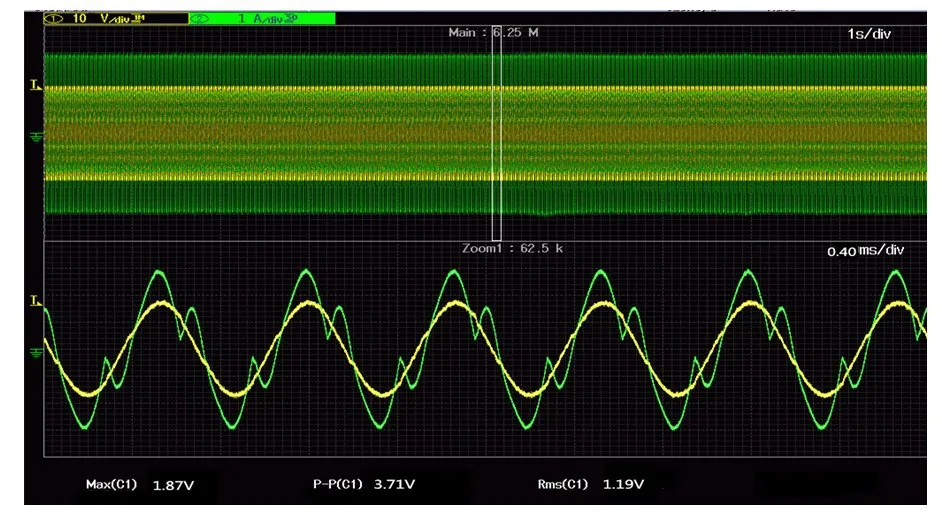
图11 分岔时输出电压与电流试验波形Fig.11Experimental waveforms of output voltage and current in bifurcation
由图12可见,输出电压电流混沌后,波形施加驱动控制法时,通过调节系统驱动控制信号强度α和驱动控制信号初相θ[17],由图13可知,在系统参数发生敏感变化时,仅在每一段时间给反馈变量以一定强度控制,可使输出电压电流波形稳定平缓并具有一定规则[18],使噪声对电路分岔混沌结构影响减小,电压模式Buck变换器输出电压电流分岔和混沌波形图可继续保持原轮廓,达到稳定周期状态及理想仿真波形,证明外加驱动控制方法有效性和优越性,使整个Buck变换器系统实现相关性能指标,并可推广到其他相关电路非线性研究,为电力电子电路稳定性设计提供可靠理论保障[19]。
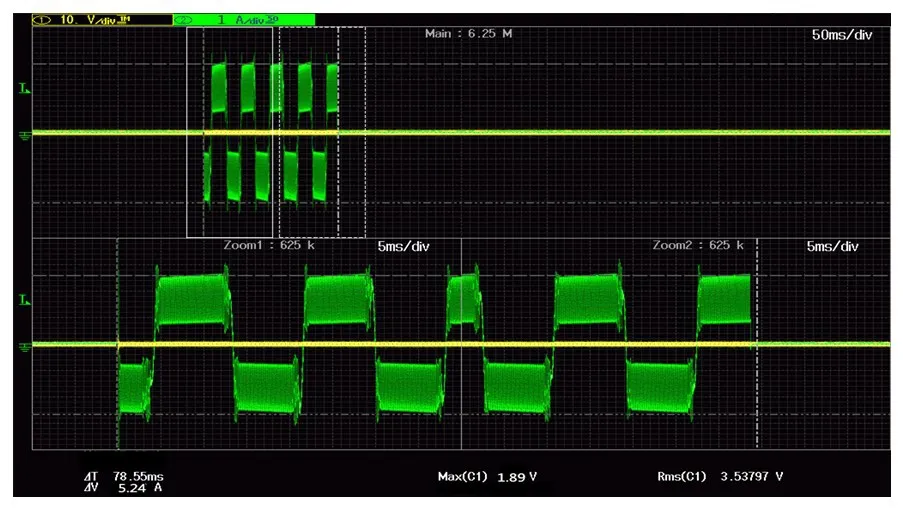
图12 混沌时输出电压与电流试验波形Fig.12Experimental waveforms of output voltage and current in chaos

图13 外加驱动控制后输出电压与电流试验波形Fig.13Output voltage and current experimental waveforms after driving control
5 结论
基于电压模式Buck变换器因参数不同取值对系统稳定性影响,本文提出外加驱动控制法抑制系统非线性现象。
a.运用Matlab/Simulink仿真软件综合分析电压模式Buck变换器电路结构及其精确数学模型,可见随着参数变化系统由稳定向混沌产生非线性现象演化。
b.在此模型基础上,对其参考电压施加一个驱动控制信号,通过调节该控制信号幅值及相位对系统优化,使电路稳定性不受参数变化影响,改善电磁兼容性能。
c.仿真结果表明,本文提出方法可抑制系统非线性现象,使系统稳定运行,保持在稳定周期1状态。该方法对DC-DC Buck变换器非线性控制策略具有一定优越性。
d.试验结果与仿真结果一致,证明外加驱动控制法可行性,非线性控制方法对电源设计和开发具有现实意义。
[1]袁雷,沈建清,肖飞.电流模式控制Buck-Boost变换器建模及非线性现象仿真[J].中南大学学报:自然科学版,2012,43(3):972-979.
[2]杨志红,姚琼荟,杨昌宏.OGY法控制混沌研究[J].海军工程大学学报,2003,15(5):60-64.
[3]卢伟国,周雒维,罗全明.电压模式BUCK变换器输出延迟反馈混沌控制[J].物理学报,2007,56(10):5648-5654.
[4]卢伟国,何启晨,周雒维,等.前馈型电压模式控制Buck变换器[J].电力自动化设备,2012,32(9):75-79.
[5]薛花,范月,王育飞.基于李雅普诺夫函数的并联型混合有源电力滤波器非线性控制方法[J].电工技术学报,2016,31(21): 133-141.
[6]匡经国,刘跃,张仁红.基于新型模糊PID控制的DC-DC变换器仿真研究[J].现代机械,2012(4):66-70.
[7]Zhou Y,Tse C K,Qiu S S,et al.Applying resonant parametric perturbation to control chaos in the Buck dc/dc converter with phase shift and frequency mismatch considerations[J].International Journal of Bifurcation and Chaos,2003,13(11):3459-3471.
[8]柴玉华,孙影,刘洪臣,等.基于随机扩频的Boost变换器非线性现象研究[J].电测与仪表,2013,50(3):81-85.
[9]王树文,王世龙,张洋.储能型光伏Quasi-TZ源逆变器研究[J].东北农业大学学报,2016,47(6):97-106.
[10]王开艳,王春芳,张玲丽.CCM和DCM模式Buck变换器建模与混沌现象仿真[J].系统仿真学报,2008,20(14):3881-3884.
[11]张波,曲颖.BUCK DC/DC变换器分岔和混沌精确离散模型及实验研究[J].中国电机工程学报,2003,23(12):99-103.
[12]周宇飞,姜丹丹,黄家成.DC-DC变换器中负载阻抗特性及其对稳定性的影响[J].中国电机工程学报,2010,30(6):15-21.
[13]刘宏新,房俊龙,陈海涛.汽车复合驱动系统中的自动控制[J].东北农业大学学报,2004,35(5):600-603.
[14]汪敏,周宇飞,江伟,等.参数共振微扰法在Buck变换器混沌反控制中的应用[J].电测与仪表,2009,46(11):32-36.
[15]房俊龙,杨平平,傅瑜,等.基于电压相角正反馈法的主动式光伏并网孤岛检测[J].东北农业大学学报,2015,46(3):103-108.
[16]罗辞勇,肖发福,唐书窗.电压模式Buck变换器混沌建模与控制研究[J].计算机仿真,2014,31(9):151-155.
[17]占萌萌,周宇飞,陈军宁.基于参数共振微扰法的直流电机混沌运动控制[J].机电工程,2012,29(11):1299-1302.
[18]Fang C C,Abed E H.Robust feedback stabilization of limit cycles in PWM DC-DC converters[J].Nonlinear Dynamics,2002,27(3): 295-309.
[19]张波.电力电子变换器非线性混沌现象及其应用研究[J].电工技术学报,2005,20(12):1-6.
Application of external drive control method in the control of nonlinear phenomenon of Buck converter
/FAN Junlong,JIN Huiya,TONG Dianxin,HE Xuedi,YANG Jingran,LIU Peng,ZHANG Huanyu(School of Electrical and Information,Northeast Agriculture University,Harbin 150030,China)
For variation of parameters when voltage mode control Buck converter in operation, which resulted in nonlinear phenomena such as bifurcation and chaos problem.With the circuit structure of Buck converter and its exact state equation model,Matlab/Simulink simulation software was used to establish the simulation model,and the simulation model has added driving control signal, through adjusting the control signal amplitude and phase,the system achieved an optimal nonlinear control results.Simulation results showed that the nonlinear phenomena in the system could be effectively suppressed by using external drive control method and the system stable operation,when the system circuit parameters changed.Verify feasibility of the method in controlling nonlinear phenomena by building a voltage mode control Buck converter experiment platform.
Buck converter;simulation;external drive control;nonlinear phenomena
TM773
A
1005-9369(2017)05-0072-10
时间2017-5-23 13:19:06[URL]http://kns.cnki.net/kcms/detail/23.1391.S.20170523.1319.020.html
房俊龙,靳惠雅,佟殿馨,等.外加驱动控制法在Buck变换器非线性现象控制中应用[J].东北农业大学学报,2017,48(5):72-81. Fan Junlong,Jin Huiya,Tong Dianxin,et al.Application of external drive control method in the control of nonlinear phenomenon of Buck converter[J].Journal of Northeast Agricultural University,2017,48(5):72-81.(in Chinese with English abstract)
2017-03-15
国家科技支撑计划课题子课题项目(2014BAD06B04-1-09)
房俊龙(1971-),男,教授,博士生导师,研究方向为电力系统自动化。E-mail:junlongfang@126.com

