有限差分法模拟多绳摩擦提升系统钢丝绳纵向振动特性

高鑫宇，吴 娟，张启顺(1.太原理工大学机械工程学院，山西 太原 030024；2.山西省矿山流体控制工程实验室，山西 太原 030024；3.矿山流体控制国家地方联合工程实验室，山西 太原 030024)

有限差分法模拟多绳摩擦提升系统钢丝绳纵向振动特性

高鑫宇1，2，3，吴 娟1，2，3，张启顺1，2，3
(1.太原理工大学机械工程学院，山西 太原 030024；2.山西省矿山流体控制工程实验室，山西 太原 030024；3.矿山流体控制国家地方联合工程实验室，山西 太原 030024)

考虑平衡钢丝绳对矿井提升系统的影响，利用Hamilton原理建立变长度提升钢丝绳纵向振动动力学模型。应用有限差分法离散化偏微分方程，并以某煤矿副立井塔式多绳摩擦提升系统为例，分析矿井提升系统运行过程中提升钢丝绳纵向振动的特性，绘制了Hilbert边际谱图以及系统能量图。数值结果表明：矿井提升系统下行过程中提升钢丝绳的伸长量不断增大，造成的是不可恢复的变形；整个运行过程中，频率为2 Hz的所占比重最大，结合多绳摩擦提升系统的参数可知，此过程不会产生共振现象；在矿井提升系统过程中，下行时能量几乎为0，上行过程中，提升系统的能量随着时间的增大逐渐增大，在井口出增大最为剧烈。因此，可以为多绳摩擦提升系统运行过程中的能量分析、动张力等分析提供一个思路。

Hamilton原理；平衡钢丝绳；纵向振动；有限差分法；Hilbert边际谱

钢丝绳是一种柔性空间螺旋结构钢制品，具有抗拉强度高、质量轻和阻尼小的特点，被广泛地应用于各种提升设备，如电梯、起重机、吊船和矿井摩擦提升机等。摩擦提升钢丝绳和电梯用钢丝绳是一种典型轴向运动弦线。电梯提升钢丝绳系统与矿井提升钢丝绳类似，电梯提升系统中横向振动和弦线与其它部件的耦合振动问题研究较多，通常采用Galerkin方法离散控制方程[1-2]。王文等[3]则采用了直接数值方法-有限差分法等来分析电梯悬挂系统变长度绳索横向振动。寇保福等[4-5]建立了提升钢丝绳和换绳过程中钢丝绳横向振动控制方程，利用多尺度法对轴向运动弦线的数值模型进行了求解。本文在上述研究基础上，采用连续弹性体建模的思想，利用有限差分法建立摩擦提升钢丝绳横向振动方程，分析不同运行阶段提升钢丝绳纵向振动规律，以及提升钢丝绳在运行过程中由于纵向振动引起的能量的变化。

1 变长度塔式摩擦提升系统纵向振动方程

本文中的模型建立和求解，始终以下面几条假设为基础[6]：①多根钢丝绳视为具有等效截面的单根钢丝绳，钢丝绳的物理参数在运动过程中始终保持恒值；② 假设提升钢丝绳由于纵向振动产生的微小弹性变形量远远小于整个弦线的长度；③不考虑钢丝绳横向和扭转对于形变量的影响。

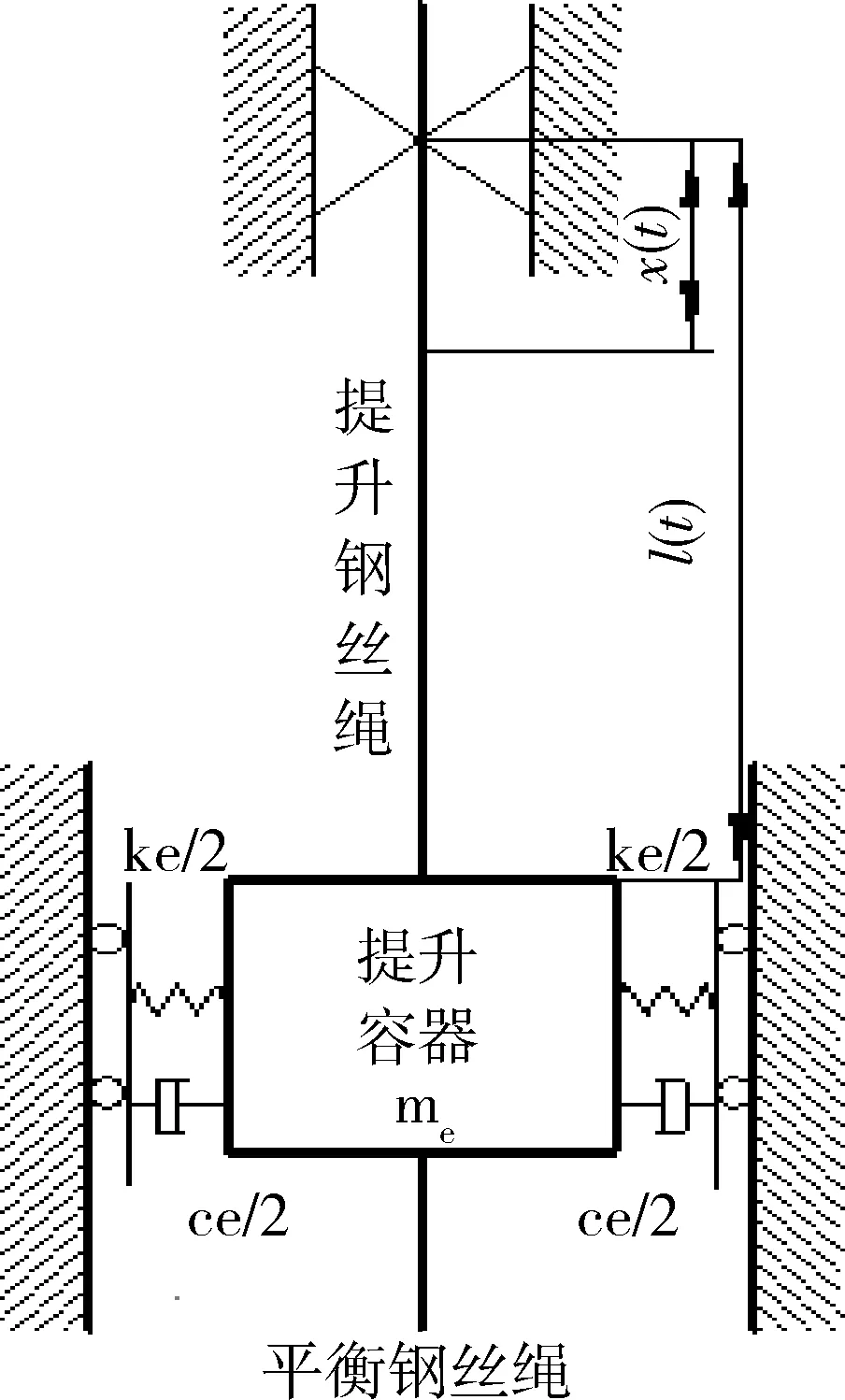
图1 摩擦提升系统模型简化示意图

系统的总动能表示为式(1)和式(2)。

(1)

me=m +(H-l(t))ρ2

(2)

式中:Vc为提升容器的绝对速度，m/s;m为提升容器总质量，kg；ρ2为提升钢丝绳密度，kg/m。

系统的弹性势能表示为式(3)。

(3)

重力势能表示为式(4)。

(4)

式中：Egs为初始重力势能，J；wc(l，t)为提升容器的纵向振动位移，mm。

利用哈密顿原理(式(5))推导出摩擦提升系统的运动方程和边界条件，可得提升钢丝绳的振动控制微分方程，见式(6)。边界条件z=l(t)，见式(7)，与纵向振动相关的能量方程见式(8)。

(5)

-ρ(g-a)-EAwzz=0，0

(6)

(7)

(8)

2 有限差分法离散

(9)

(10)

式中，i=1，2，…，n-1。

(11)

将式(9)、式(10)和式(11)代入式(6)和式(7)中，联立可得到如式(12)所示的常微分方程。

(12)

为了编辑方便与简化，定义式(13)～(15)。

(13)

(14)

(15)

矩阵M，C，K及向量F中的元素由下列各式确定，矩阵中的其他元素均为0。

M(i，i)=ρ，i=1，2，…，n-1；

M(n，n)=mehl(2EA-hρl2)；

K(i，i)=-2Φ2(ξi)，i=1，2，…，n-1；

K(i，i+1)=Φ2(ξi)+Φ1(ξi)-Φ3(ξi)，

i=1，2，…，n-1；

K(i+1，i)=Φ2(ξi)-Φ1(ξi)+Φ3(ξi)，

i=1，2，…，n-2；

K(n，n-1)=-2meE2A2；

K(n，n)=2meE2A2；

3 仿真分析

以某煤矿塔式多绳摩擦提升系统的运行参数为例。摩擦提升系统运行状态参数分别为：lmax=263 m，vmax=6 m/s，amax=0.25 m/s2。提升容器质量m=50 000 kg，EA=80 000 MPa。提升钢丝绳线密度51.12 kg/m。平衡钢丝绳线密度50.4 kg/m。提升系统的运行曲线如图2所示。

结合提升系统运行曲线以及上述系统参数，通过Matlab逐步积分法解常微分方程可以得到提升钢丝绳纵向实时振动位移与时间的关系，结果如图3所示。

图2 提升系统运行曲线

图3 纵向振动时程曲线图

由图3可知，矿井提升系统下行过程中提升钢丝绳的伸长量不断增大，由于钢丝绳提升重物的拉力引起钢丝绳的扭转，造成了提升钢丝绳上部的松捻与下部的紧捻，产生如图所示的波动的变形量，但是整体来说伸长量是增大的，与物体的塑性变形有所区别。结论与文献[2]相符合，同时也验证了有限差分法的正确性。

由于考虑了平衡钢丝绳的影响，因此多绳摩擦提升系统的频率是不断变化的，普通的傅里叶变换已经无法满足研究要求。

图4是将钢丝绳振动信号作为输入，进行EMD变换后求得Hilbert边际谱图，从图4中可以看出整个运行过程中，频率为2 Hz的所占比重最大，结合多绳摩擦提升系统的参数可知，此过程不会产生共振现象。此方法也为钢丝绳故障诊断提供了新思路。

对能量方程式(8)通过Simpson算法，可以求解得到提升钢丝绳在运行过程中产生的能量变化情况，结果如图5所示。

图4 Hilbert边际谱图

图5 提升钢丝绳振动能量图

由图5可知，在矿井提升系统过程中，下行时能量几乎为0。上行过程中，提升系统的能量随着时间的增大逐渐增大，在井口处增大最为剧烈。可以为多绳摩擦提升系统运行过程中的能量分析提供一个思路。从图5(b)可以看出，矿井提升系统启动时会有能量的急剧变化，这也为提升系统在制动、受冲击时的动张力、动位移变化提供理论研究基础。

4 结 论

1)本文针对矿井提升系统变长度提升钢丝绳时变特性，利用Hamilton原理建立了提升钢丝绳纵向振动偏微分方程。利用有限差分法将连续的空间变量离散化得到变系数的常微分方程组，通过Matlab软件数值仿真得到纵向振动响应曲线图。与参考文献[2]进行了比较，验证了本文方法的有效性。

2)将钢丝绳振动信号作为输入，进行EMD变换后求得Hilbert边际谱图，可以看出整个运行过程中频率为2Hz的所占比重最大，结合多绳摩擦提升系统的参数可知，此过程不会产生共振现象。此方法也为钢丝绳故障诊断提供了新思路。

3)通过Simpson算法，运用Matlab进行仿真分析，得到了矿井提升系统运行过程中的能量变化曲线，可以为多绳摩擦提升系统运行过程中的能量分析提供一个思路。下行矿井提升系统启动时会有能量的急剧变化，这也为提升系统在制动、受冲击时的动张力，动位移变化提供理论研究基础。

4)本文所研究的提升钢丝绳纵向振动特性分析的内容，为多绳摩擦提升系统提升钢丝绳振动特性提供理论依据，并且对多绳摩擦提升机势能驱动快速换绳装置的进一步研究具有一定的参考价值。

[1] 梁敏,寇子明. 立井提升系统卡罐时钢丝绳的横向振动分析[J]. 煤炭技术,2015,34(1):289-291.

[2] 张敏,梁敏. 矿井提升系统首绳的纵向振动分析[J]. 煤矿机械,2015，36(5):137-139.

[3] 王文,钱江.有限差分法模拟电梯悬挂系统横向受迫振动[J].振动工程学报,2014,27(2):180-185.

[4] 寇保福,刘邱祖,刘春洋，等.矿井柔性提升系统运行过程中钢丝绳横向振动的特性研究[J].煤炭学报,2015,40(5):1194-1198.

[5] 寇保福,刘邱祖,李为浩，等.提升系统换绳过程中钢丝绳横向振动行为分析[J].煤炭学报，2015,40(S1):247-251.

[6] 包继虎,张鹏,朱昌明.变长度提升系统钢丝绳纵向振动特性[J].振动与冲击,2013(15):173-177.

Longitudinal vibration characteristics of multi-rope friction hoisting system by the finite difference method

GAO Xinyu1，2，3，WU Juan1，2，3，ZHANG Qishun1，2，3

(1.College of Mechanical Engineering，Taiyuan University of Technology，Taiyuan 030024，China；2.Shanxi Province Mineral Fluid Controlling Engineering Laboratory，Taiyuan 030024，China；3.National-local Joint Engineering Laboratory of Mining Fluid Control，Taiyuan 030024，China)

Considering the impact of the balance of wire rope to the mine hoisting system and using Hamilton principle to establish the variable length of steel rope longitudinal vibration dynamic model of mine hoisting system.The finite difference method was used to discretize the partial differential equation to ordinary differential equation.The mine hoisting system was used to the example to analysis the regular of the longitudinal vibration of wire rope，the Hilbert marginal spectrum and the energy diagram of the system are plotted.The simulation results showed that the elongation of mine hoisting rope system is increasing in the descending process of mine hoisting system，which is unrecoverable deformation；during the whole process of operation，the frequency of 2Hz is the largest，according to the parameters of the multi rope friction hoisting system，it cannot produce resonance phenomenon；in the process of mine hoist system，the energy is almost 0 in downlink，while in the uplink process，the energy of the system increases with the time increasing，the most dramatic increase in pithead.Therefore，it can provide an idea for energy analysis and dynamic tension analysis of multi rope friction hoisting system.

Hamilton principle；balanced wire rope；longitudinal vibration；finite difference method；Hilbert marginal spectrum

2017-03-02 责任编辑：宋菲

山西省科技创新项目资助(编号：2014101001)

高鑫宇(1994-)，内蒙古乌兰察布人，硕士研究生，研究方向为机电液一体化，E-mail：gaoxy8623@163.com。

TD532

A

1004-4051(2017)06-0157-04