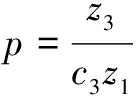基于自适应步长ADMM的直流配电网分布式最优潮流

韩禹歆 陈来军 王召健 刘 炜 梅生伟

(1.电力系统及发电设备控制和国家重点实验室(清华大学电机系) 北京 100084 2.陕西省地方电力集团有限公司 西安 710061)



基于自适应步长ADMM的直流配电网分布式最优潮流

韩禹歆1陈来军1王召健1刘 炜2梅生伟1

(1.电力系统及发电设备控制和国家重点实验室(清华大学电机系) 北京 100084 2.陕西省地方电力集团有限公司 西安 710061)

直流配电网的发展前景广阔，其最优潮流(OPF)问题关系到电网经济运行，具有重要的工程意义。针对放射状直流配电网，以二阶锥规划(SOCP)凸松弛理论为基础，建立了考虑电压、电流、功率约束的SOCP-OPF凸规划模型，并提出一种基于交替方向乘子法(ADMM)的分布式最优潮流计算方法，以解决传统集中式优化方式面临的诸多难题。相比已有研究，该方法在各节点配置计算单元，无需全局协调或分层分区，利用相邻主体间少量的信息传递即可通过并行计算得出全局最优解；优化模型中考虑了配电线路传输电流限制，约束条件更全面；计算方法中设计了自适应步长调整机制，计算效率较高。IEEE 33节点和IEEE 123节点的算例分析验证了所提算法的准确性和良好的收敛性。

直流配电网 分布式优化 最优潮流 交替方向乘子法 自适应步长

0 引言

随着分布式发电(Distributed Generation，DG)技术及电力电子技术的发展，直流配电网已在诸多方面具备一定的经济与技术优势。以光伏、燃料电池等为代表的DG在直流配电网接入时可省去DC-AC环节，有效降低成本和损耗[1]。此外，直流配电网还具有传输容量大、线路成本低、配电损耗小、供电可靠性高等多方面优势[2]，已逐渐成为热点研究领域。其中，直流配电网的最优潮流(Optimal Power Flow，OPF)问题，由于对其经济高效运行乃至分布式电源技术发展的重要意义，更是受到了广泛的关注[3]。

最优潮流问题作为电力系统中的经典问题，其求解方法层出不穷，包括基于数学规划理论的继承式线性/二次规划法[4]、置信域法[5]、拉格朗日-牛顿法[6]、内点法[7]等，以及各类智能算法如量子免疫算法[8]、粒子群算法[9]等。需要提出的是，以上优化方法大多基于集中式优化方法，在实际应用中需通过调度中心收集并处理全局信息，经过集中计算后下达调控指令。随着DG以及其他各类可控设备的大量接入，集中式优化对通信的要求将很难满足，同时中控单元对计算和存储资源的需求量也将急剧增加[10]。此外，在DG与配电网归属于不同利益主体的情况下，集中式优化将难以有效保护DG主体的信息隐私[11]。在此背景下，分布式优化方法应运而生，其特点是以并行计算和局部通信克服了传统集中式优化方法的瓶颈，无需全局协调，且对分布式电源接入具有较强的适应性[12]。在主动配电网技术发展的驱动下，分布式优化有望成为未来配电网优化调度运行的重要方式[13]。

目前分布式优化的研究主要集中在交流配电网场景下。文献[14，15]将配电网划分成多个区域，提出的区域内集中式、区域间分布式的优化策略。文献[16，17] 提出了以节点为主体的完全分布式优化方法，无需考虑区域划分问题。文献[18]考虑了三相配电网不平衡的特点，采用半正定规划(Semidefinite Program，SDP)凸松弛方法将OPF模型凸化后进行分布式求解。在直流配电网研究方面，文献[19]提出了直流配电网OPF模型的二阶锥规划(Second-Order Cone Programming，SOCP)凸松弛理论，为OPF问题的全局寻优求解打下重要理论基础。但总体而言，目前对直流配电网分布式OPF求解的研究相对较少。如前文所述，分布式电源接入便捷是直流配电网的优势之一，多DG配电网也将是未来直流配电网的重要应用场景。随着未来分布式电源数量的不断增多，传统集中式直流配电网优化调度将受到挑战。因此，直流配电网分布式优化问题的研究对其未来发展和分布式电源应用具有重要前瞻性意义[20，21]。

本文在SOCP凸松弛理论的基础上，考虑了电压、电流以及功率约束建立了SOCP-OPF优化模型，并提出一种基于交替方向乘子法(Alternating Direction Method of Multipliers，ADMM)的自适应步长分布式OPF高效算法，通过临近节点的信息传递，实现了放射状直流配电网OPF问题的分布式求解。与已有分布式优化算法相比，本文方法无需全局协调或分层分区，属于完全分布式优化算法；OPF模型考虑了线路最大传输电流约束，实用性较强；算法内部无需再调用优化迭代子过程，且设计有自适应步长调节机制，计算效率较高。最后用算例证明了本文算法具有良好的收敛性和准确性。

1 优化模型与SOCP凸松弛

首先，将放射状直流配电网建模为一个如图1所示的树状有向图T=(N,E)，有向图中的顶点代表配电网中的节点，边代表配电网中的线路。其中N={1,2,…,n}为节点的集合，令根节点编号为1，N+=N{1}表示除根节点外所有节点的集合；E为线路的集合，规定线路方向总是由根节点指向末端节点。设图中节点i与节点j由线路相连，则i，j称为相邻节点，记为i～j；若线路方向由i指向j，则节点j称为节点i的子节点，记为j∈Ci，其中Ci为节点i子节点的集合，作为数值时表示节点i的子节点数；节点i为节点j唯一的母节点，记为i∈Aj，其中Aj代表节点j母节点的单元素集合。规定母节点编号总是小于子节点编号。

基于上述定义，典型的直流配电网OPF模型可表示为[22]

(1)

系统目标函数为发电总成本时，令功率输入节点pi为正值，输出节点为负值，则有

(2)

式中，ai为各节点的发电成本系数，一般在公共耦合点(PointofCommonCoupling，PCC)和DG接入节点为大于0的常数，在负荷节点处为0。令系统任意节点ai=1，则式(2)表示系统网损。

约束条件方面，考虑到实际配电网中配电线路的最大传输电流限制，本文除常规潮流平衡约束、节点注入功率约束和节点电压上下限约束之外，也考虑了支路电流上下限约束。相对于交流配电网，直流配电网中的OPF无需考虑有功功率和无功功率之间的耦合，有利于提升计算效率，实现快速乃至实时的优化调度。

由于潮流平衡方程的非线性，模型式(1)为非凸规划问题，一般的优化算法无法保证其求解的收敛性与最优性。凸松弛理论可将式(1)中的潮流平衡约束松弛成为凸约束，从而将式(1)转化成凸规划，进行求解[23-25]。其中二阶锥规划凸松弛是常见的凸松弛方法，具有模型复杂度低、计算速度快等优势，在放射状配电网中具有良好的适用性。根据文献[19]的SOCP凸松弛理论，令k∈Ai，可将式(1)转换为式(3)所示的凸规划问题(SOCP-OPF)。

(3)

若凸松弛后的优化模型最优解与原模型相同，称其为精确的。对于放射状电网，在满足微弱条件的情况下可保证SOCP凸松弛的精确性[22]，因此不妨设SOCP-OPF模型式(3)精确，可通过凸规划式(3)完成直流配电网OPF问题的求解。为克服前文所述的常规集中式优化方式在未来主动配电网中应用的弊端，接下来本文将基于ADMM方法提出一种分布式优化算法对式(3)进行求解。

2 分布式OPF算法

2.1 交替方向乘子算法

ADMM方法结合了对偶分解法解耦的思想和乘子法收敛速度快的特点，具有收敛性好，鲁棒性强等优点，在分布式优化中较为适用[16]。传统的ADMM方法可用于求解如下优化问题

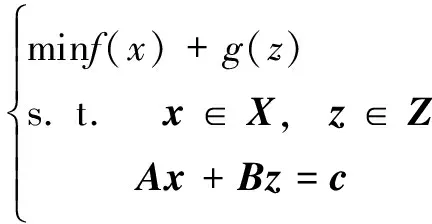
(4)

式中，X、Z为凸集，模型式(4)为凸规划。令λ为其中等式约束的拉格朗日乘子，则增广拉格朗日算子为

Lρ(x,z,λ)=f(x)+g(z)+λT(Ax+Bz-c)+

(5)

式中，ρ为常数，ρ≥0。

ADMM方法迭代过程分为x迭代、z迭代和λ迭代，各迭代过程的具体表达式为

xk+1=argminx∈XLρ(x,zk,λk)

(6)

zk+1=argminz∈ZLρ(xk+1,z,λk)

(7)

λk+1=λk+ρ(Axk+1+Bzk+1-c)

(8)

迭代计算中的原始残差和对偶残差分别为

rk=‖Axk+Bzk-c‖

(9)

sk=ρ‖ATB(zk-zk-1)‖

(10)

凸规划问题采用ADMM方法计算可保证收敛至最优解[26]。

本文提出的分布式ADMM算法主要包括3步：首先将OPF模型处理为ADMM方法可以求解的形式，并根据分布化计算的要求设计各个节点的本地变量集；然后将迭代过程分解为各节点的本地计算过程；最后设计一种自适应步长调节机制提升算法的效率。

2.2 分布式OPF建模

式(3)的OPF问题可简化为

(11)

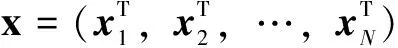
(12)

通过引入影子变量z，上述步骤将式(11)中的等式约束和不等式约束进行了解耦，使原变量x和影子变量z分别只受一部分条件的约束，在每个迭代周期中分别进行更新，最后由等式约束x-z=0对二者值进行统一。此方法减少了变量分布式迭代过程中子优化问题的约束条件，使其具有解析解，从而令各分布式计算单元无需运行复杂的优化迭代算法即可完成迭代计算，降低了计算复杂性。这一点将在后续章节中有所体现。

值得注意的是，式(12)中的x-z=0是作为形如式(4)中Ax+Bz=c的等式约束条件存在，并不代表x和z在任何时刻完全相等。ADMM作为一种数值优化解法，变量x和z将分别通过不同的迭代更新过程共同逼近最优解，因此在采用ADMM求解式(12)过程中，x和z数值上可能存在差异。

循此思路可将式(3)转换为式(4)的形式。对于节点i∈N，令式(3)中全部本地电气量组成变量x及变量z，即

(13)

(14)

同时对于优化模型中涉及的母节点相关量，建立一个变量表示子节点j对母节点i相关信息的估计，即

xi,j=(vi,j,Pij,j)Tj∈Ci

(15)

式中，vi,j、Pij,j为子节点j对其母节点i的vi、Pij值的估计值。为方便后续计算，定义变量z的子变量为

(16)

令k∈Ai，可建立如下所示的优化模型：

(17)

(18)

Pik+Pki,i=zkilkii∈N+

(19)

vi-vk,i+zki(Pki,i-Pik)=0i∈N+

(20)

(21)

(22)

(23)

(24)

xi-zi=0i∈N

(25)

(26)

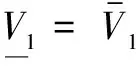
(27)

2.3 分布式OPF求解

式(17)～式(26)的增广拉格朗日算子可写为以下两种完全等价的形式

Lρ(x,z,λ,μ)

(28)

Lρ(x,z,λ,μ)

(29)

对于任意节点i，式(28)关注其与母节点k之间的关系，涉及到式(17)～式(26)中x约束的母节点相关电气量，因此x迭代过程采用式(28)的表达形式；而式(29)关注节点与其子节点j之间关系，各变量均来自本地，无需与相邻节点进行通讯，对于仅考虑z约束的z迭代过程较为适用。下面将分别介绍x迭代、z迭代和λ迭代过程的分布化。

1)分布式x迭代。

结合式(6)和式(28)可将x迭代过程表示为

xk+1=argminLρ(x,zk,λk,μk)

(30)

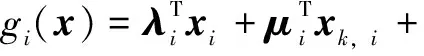
(31)

因此，节点i的x迭代子过程求解的子优化问题如式(32)所示，其中以xi、xk,i为优化变量，其余变量z、λ、μ固定为常数。节点i的计算单元对式(32)进行优化求解后，更新xi、xk,i的数值，即完成了一次x迭代。

(32)

进一步，式(32)可抽象为优化问题式(33)，它有解析解，并可通过式(34)计算得出。

(33)

(34)

需要说明的是，每次x迭代前节点i需要与其母节点k通信获取xk,i、zk、μi的数值，x迭代完成后再将新的xk,i值返回母节点k，这也将是整个x-z-λ迭代周期中所需唯一的一次节点间通信。设k∈Ai，则通信机制如图2所示。

图2 x迭代前后通信机制示意图Fig.2 Schematic diagram of communication before and after x-iteration

图2 x迭代前后通信机制示意图Fig.2 Schematic diagram of communication before and after x-iteration

2)分布式z迭代。

z约束均为本地约束，采用式(29)的拉式乘子表达形式，可无需与相邻节点进行通信。结合式(7)，节点i的本地z迭代过程可表示为

zk+1=argminLρ(xk,z,λk,μk)

(35)

(36)

(37)

此过程以zi为优化变量，其它变量为常数进行迭代更新，所需参数均可从本地获取。节点1的子问题容易求解，而对于节点i∈N+，可令

(38)

则式(37)可表示为

(39)

式中，y3,y5,…,y4+Ci可直接通过式(40)求解；其他变量值通过求解优化问题式(41)获得。

(y3,y5,y6,…,y4+Ci)

(40)

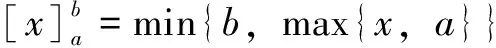
(41)

式(41)通过分情况讨论具有解析解，具体解法见附录。

3)分布式λ迭代。

结合式(8)，节点i的λ迭代过程同样仅需本地信息计算，即

λi=λi+ρ(xi-zi)

(42)

(43)

综上所述，本文算法中整个x-z-λ迭代周期内的运算均具有解析形式，各计算单元无需运行任何优化算法，计算效率较高；同时各计算单元仅需每个周期内与母节点进行一次数据的收发即可独立完成迭代过程，因此本文方法属于完全分布式优化算法。

2.4 步长自适应调节机制

在ADMM方法中，步长ρ的选取对算法收敛速度有较大的影响，其选取不当可能导致原始及对偶残差中某一项收敛速度远慢于另一项，延长算法的计算时间。因此本文提出一种自适应步长调节机制，即

(44)

上述自适应调节机制的基本思路是平衡原始残差及对偶残差收敛速度，避免因二者其一收敛过慢。当原始残差rk相对较大时，增大步长，即可增大式(28)和式(29)中范数项比重，促进x与z的接近，由此加快rk收敛；当原始残差rk相对较小时，减小步长可减少目标函数的震荡，促进z变量的收敛。本文以rk、sk之间比值的对数作为调整步长的参照量，根据残差大小对比灵活调整步长的同时，可利用对数函数的饱和性有效避免步长调节幅度过大导致算法迭代过程的振荡。

3 算例分析

3.1IEEE33节点算例(算例1)分析

相对于集中式优化中计算单元能够掌握全局信息，分布式优化中各相邻主体间仅有少量数据的传递，因此能否保证算法在较少迭代次数内收敛至最优解是分布式优化的主要难点。本文将图3所示的标准IEEE33节点配电网系统修改为直流配电网，并进行分布式OPF仿真测试以验证算法求解过程的收敛性及最优性。

图3 算例1的拓扑结构Fig.3 Topology of case 1

各节点电压上、下限分别设置为1.07(pu)和0.93(pu)，系统中接入5个分布式电源，根节点1为平衡节点，电压固定为1.05(pu)。同时按照配电网常用的LGJ-70型号线路，支路电流上限设置为275A。算例分析采用的仿真环境为Intel(R)Core(TM)i5-2 540MCPU，2.60GHz，8GB内存，仿真平台为Matlab2012b。

为验证结果的准确性，本文同时将采用CVX优化工具中的SDPT3算法进行集中式优化计算，将其结果与本文算法进行比较。

首先，令目标函数为系统网损，即各节点成本系数均为1进行仿真测试，系统网损以及残差随迭代过程的变化曲线如图4和图5所示。

图4 算例1网损迭代变化曲线Fig.4 Power loss during iteration in case 1

图5 以网损为目标时残差迭代变化曲线Fig.5 Residual with minimization of power loss during iteration

在ADMM法中，原始残差体现了模型的不可行度，对偶残差则可用于判断迭代是否收敛至最优解，两者的变化趋势反映算法的收敛特性。从图4和图5可以看到，本文所提算法通过67次迭代计算收敛至最优解，具有良好的收敛性，且目标函数最终收敛至与集中式优化相同的结果12.09kW。本文算法计算结果与集中式优化结果比较见表1。

表1 IEEE 33节点算例计算结果对比

由表1可见，在误差允许的范围内，本文所提的分布式算法计算结果与集中式算法相比计算结果完全一致，验证了本文算法具有较好的准确性。

计算效率方面，本文算法计算时间为1.20 s，考虑到本文算法在单个计算机上为串行仿真，故单节点平均计算时间为1 200/33=36.36 ms，而集中式优化计算时间为2.46 s，本文算法具有明显优势。

保持其他参数不变，改变仿真的目标函数，令大电网的成本系数为1，DG的成本系数为0.5，负荷节点的成本系数为0，则有

(45)式中，G为DG接入节点的集合。此时目标函数代表当大电网发电成本为DG的两倍时系统的总发电成本。

目标函数及残差随迭代过程的变化曲线如图6和图7所示。可见，在以发电成本为目标函数的情况下，本文算法同样展现了良好的收敛性。同时本文算法与集中式优化结果一致，均为5台DG满发，目标函数最小值为1 715 kW。与以网损为目标函数时的仿真结果相比较，由于本次仿真DG的发电成本低于大电网的发电成本，因此系统偏向于消纳DG发出的电能，体现了实际配电网中优先消纳清洁能源，避免弃风、弃光的原则。本次分布式计算总时间2.14 s，节点平均耗时2140/33=64.85 ms，而集中式优化计算耗时2.45 s。受条件限制本文算例中不是多台电脑独立计算再相互通信，而是在一台电脑上串行计算后再交换信息，此时所需的计算时间比集中式长。然而，在实际运行时，每个节点各自计算，是并行过程，且单个节点的计算量较小，因而单个节点的计算时间较集中式优化短。

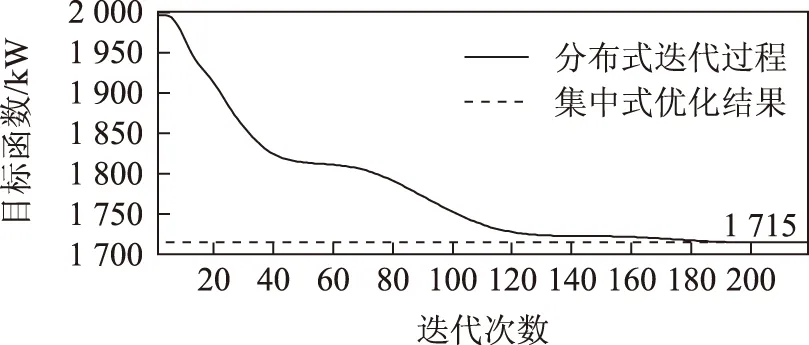
图6 算例1发电总成本迭代变化曲线Fig.6 Generation cost during iteration in case 1

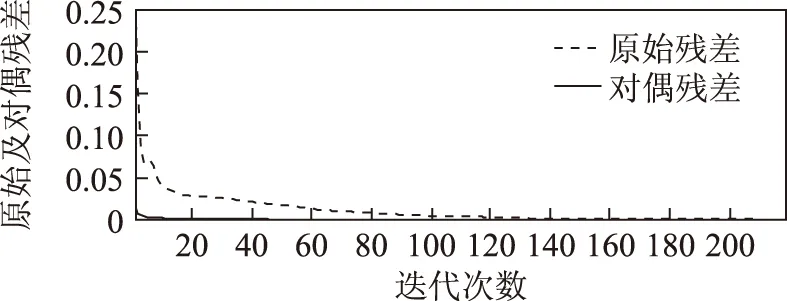
图7 以发电总成本为目标时残差迭代变化曲线Fig.7 Residual with minimization of generation cost during iteration

为验证本文提出的自适应步长调节机制的有效性，以网损为目标函数，其他参数不变，考察有无自适应步长调节机制的迭代次数，结果对比如图8所示。引入自适应步长调节机制前，算法迭代过程中原始残差收敛较慢，导致算法迭代110次后才能收敛；引入自适应调节机制后，原始残差收敛速度明显加快，迭代次数减少至67次。

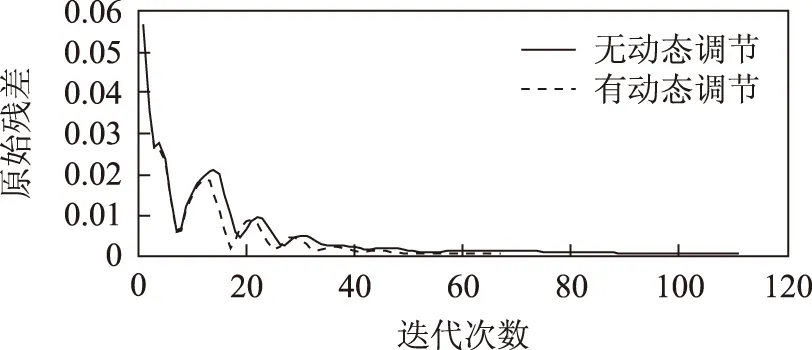
图8 自适应步长调节对算例1收敛性的影响Fig.8 Comparasion of iteration with and without self-adaptation in case 1

3.2 IEEE 123节点算例(算例2)分析

为进一步验证本文所提方法的有效性，以下将以IEEE 123节点配电网系统为例，进行分布式OPF仿真。修改后的IEEE 123节点配电网系统如图9所示。主要的修改为在系统中接入7个分布式电源，分别位于节点11、34、33、83、96、85、114。各节点电压上、下限分别设置为1.07(pu)和0.93(pu)。

图9 算例2的拓扑结构Fig.9 Topology of case 2

以网损为目标的仿真结果如图10和表2所示。其中，图10给出了求解过程中网损的变化，表2比较了集中式优化结果与本文算法结果。

图10 算例2网损迭代变化曲线Fig.10 Power loss during iteration in case 2

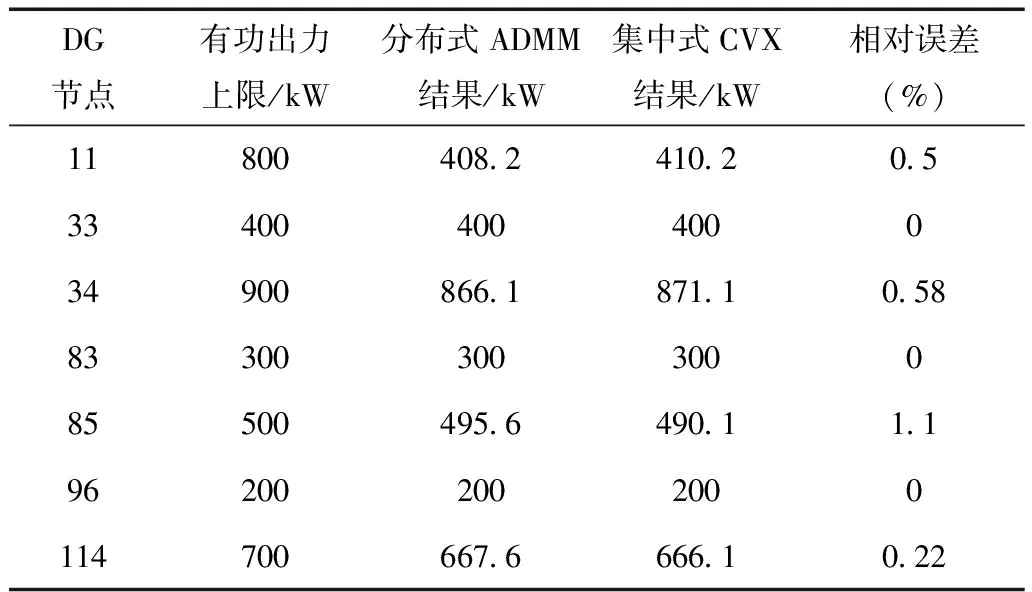
DG节点有功出力上限/kW分布式ADMM结果/kW集中式CVX结果/kW相对误差(%)11800408 2410 20 533400400400034900866 1871 10 5883300300300085500495 6490 11 1962002002000114700667 6666 10 22

由图10可知，本文算法通过1 130次迭代计算即可收敛至最优解。

由表2可知，本文算法所得结果与集中式优化结果的相对误差小于1.2%，证明了本文算法具有较好的准确性。

计算效率方面，本文算法计算时间为119 s，考虑到本文算法在单个计算机上为串行仿真，故单节点平均计算时间为119 s/123=0.963 s，而集中式优化计算时间为5.27 s，本文算法具有明显优势。较高的计算效率也有助于本算法未来在配电网中实现在线优化和实时调度。

保持其他参数不变，改变仿真的目标函数，令大电网的成本系数为1，DG的成本系数为0.5，负荷节点的成本系数为0。总发电成本随迭代过程的变化曲线如图11所示。

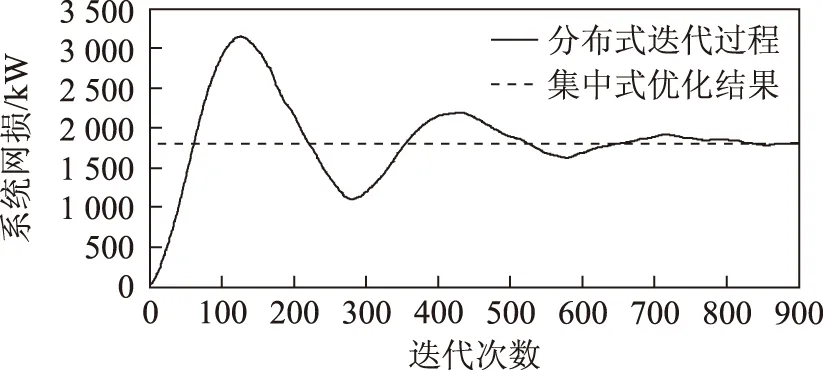
图11 算例2发电总成本迭代变化曲线Fig.11 Generation cost during iteration in case 2

由图11可知，在以发电成本为目标函数的情况下，本文所提算法通过900次迭代计算收敛至最优解。同时本文算法与集中式优化结果一致，目标函数最小值为1 805 kW。本次分布式计算总时间109 s，节点平均耗时109 s/123=0.886 s，而集中式优化计算耗时9 s。由此可见，本文所提的分布式算法与集中式优化相比具有明显的计算效率优势。

由图12可知，未引入步长自适应调节机制时，算法迭代900次后才能收敛；而引入自适应调节机制后，原始残差收敛速度明显加快，迭代次数减少至460次。

图12 自适应步长调节对算例2收敛性的影响Fig.12 Comparasion of iteration with and without self-adaptation in case 2

4 结论

本文针对放射状直流配电网的最优潮流问题，建立了考虑支路电流约束的SOCP-OPF凸规划模型，并提出了一种基于ADMM可自适应调节步长的分布式OPF求解方法。相比于传统集中式优化方法，该算法仅需节点间局部通信即可通过并行计算求出全局最优解，无需全局协调或分层分区，且具有通信要求低、计算量分散、适应性强、保证数据隐私等优势。本方法在子优化问题求解中无需调用优化迭代过程，且具备自适应步长调节机制，计算效率较高，在实时优化调度方面具有一定应用前景。算例分析也验证了其较好的收敛性及准确性。

附 录

式(41)可简化为

(A1)

其拉格朗日算子为

λ1(z1-z1max)-λ2(z1-z1min)+

γ1(z2-z2max)-γ2(z2-z2min)

(A2)

根据KKT条件，式(A1)的最优解满足如下最优性条件

(A3)

由于式(A1)为凸规划，且问题存在可行解，因此当z1max≥z1min≥0、z2max≥z2min≥0时，式(A3)存在唯一最优解，下面分情况讨论最优解。

情况1：若μ=0，则式(A3)可化为

(A4)

若忽略式(A4)中最后一个不等式约束，则其的解为

(A5)

情况2：若μ>0，则式(A3)可化为

(A6)

2z2+c2-k2μ+γ1-γ2=0

(A7)

(A8)

λ1(z1-z1max)=0λ1≥0z1≤z1max

(A9)

λ2(z1min-z1)=0λ2≥0z1≥z1min

(A10)

γ1(z2-z2max)=0γ1≥0z2≤z2max

(A11)

γ2(z2min-z2)=0γ2≥0z2≥z2min

(A12)

(A13)

将式(A13)代入式(A7)可得

(A14)

将式(A14)代入式(A6)与式(A8)得

(A15)

(A16)

为求出最优解，按顺序考虑如下4种情况：

1)若z1、z2均达到上限值或下限值。

不妨设z1、z2均为上限值即z1=z1max,z2=z2max，可知λ2=γ2=0，由式(A13)的正根可求出z3值。将结果代入式(A14)～式(A16)可得出μ、λ1、γ1，若μ、λ1、γ1值均非负，则结果为式(A1)的最优解，否则进入下一情况。其他z1,z2均达到限值情况以此类推。

2)若z1达到上限值或下限值且z2min

不妨设z1=z1max，有λ2=γ1=γ2=0。将z1值代入式(A16)得出

(A17)

式(A17)若存在正实根z3，可由式(A15)、式(A13)与(A14)先后求出λ1、z2、μ，若μ、λ1非负，则该解为式(A1)的最优解，否则考虑下一情况。z1=z1min情况类似。

3)若z2达到上限值或下限值且z1min

不妨设z2=z2max，有λ1=λ2=γ2=0。将式(A13)代入式(A15)和式(A16)中，得

(A18)

(A19)

式(A18)和式(A19)消去(c2+γ1)可得

(A20)

式(A20)若存在正实根z3，可由式(A18)、式(A19)、式(A13)、式(A14)分别求出γ1、z1、μ，若μ、γ1非负，则该解为式(A1)的最优解，否则考虑下一情况。z2=z2min情况类似。

4)若z1min

(A21)

(A22)

式(A21)与式(A22)的两端分别相除，得

(A23)

化简得

(A24)

将式(A24)代入式(A22)有

(A25)

求解出式(A25)的正实根代入式(A24)得出z1，随之由式(A13)计算出z3、z2，再利用式(A14)求出μ，若其非负，则该解为问题式(A14)的最优解。

[1] 周逢权，黄伟.直流配电网系统关键技术探讨[J].电力系统保护与控制，2014，42(22)：62-67.ZhouFengquan，HuangWei.StudyonthekeytechnologyofDCdistributionpowernetwork[J].PowerSystemProtectionandControl，2014，42(22)：62-67.

[2] 吴翔宇，沈沉，赵敏，等.基于公共母线电压的微电网孤网运行下垂控制策略[J].电工技术学报，2015，30(24)：135-141.WuXiangyu，ShenChen，ZhaoMin，etal.AdroopcontrolmethodbasedonPCCbusvoltageinislandedmicrogrid[J].TransactionsofChinaElectrotechnicalSociety，2015，30(24)：135-141.

[3] 徐殿国，刘瑜超，武健.多端直流输电系统控制研究综述[J].电工技术学报，2015，30(17)：1-12.XuDianguo，LiuYuchao，WuJian.Reviewoncontrolstrategiesofmulti-terminaldirectcurrenttransmissionsystem[J].TransactionsofChinaElectrotechnicalSociety，2015，30(17)：1-12.

[4]ContaxisGC，DelkisC，KorresG.Decoupledoptimalloadflowusinglinearorquadraticprogramming[J].IEEETransactionsonPowerSystems，1986，1(2)：1-7.

[5]WangMin，LiuShengsong.Atrustregioninteriorpointalgorithmforoptimalpowerflowproblems[J].InternationalJournalofElectricalPower&EnergySystems，2005，27(4)：293-300.

[6]BaptistaEC，BelatiEA，daCostaGRM.Logarithmicbarrier-augmentedLagrangianfunctiontotheoptimalpowerflowproblem[J].InternationalJournalofElectricalPower&EnergySystems，2005，27(7)：528-532.

[7]TorresGL，QuintanaVH.Aninterior-pointmethodfornonlinearoptimalpowerflowusingvoltagerectangularcoordinates[J].IEEETransactionsonPowerSystems，1998，13(4)：1211-1218.

[8]VanajaB，HemamaliniS，SimonSP.ArtificialImmunebasedEconomicLoadDispatchwithvalve-pointeffect[C]//TENCON2008，Hyderabad，India，2008：1-5.

[9] 黄飞腾，南余荣，翁国庆，等.计及监测可信度的扰动源定位粒子群算法[J].电工技术学报，2016，31(16)：215-222.HuangFeiteng，NanYurong，WengGuoqing，etal.Particleswarmoptimizationofdisturbancesourcelocationwithmonitoringreliability[J].TransactionsofChinaElectrotechnicalSociety，2016，31(16)：215-222.

[10]吕林，王佳佳，刘俊勇，等.基于多粒子群分层分布式优化的配电网重构[J].电力系统保护与控制，2009，37(19)：56-68.LüLin，WangJiajia，LiuJunyong，etal.Adistributedhierarchicalstructureoptimizationalgorithmbasedpoly-particleswarmforreconfigurationofdistributionnetwork[J].PowerSystemProtectionandControl，2009，37(19)：56-68.

[11]洪奕光，翟超.多智能体系统动态协调与分布式控制设计[J].控制理论与应用，2011，28(10)：1506-1512.HongYiguang，ZhaiChao.Dynamiccoordinationanddistributedcontroldesignofmulti-agentsystems[J].ControlTheory&Applications，2011，28(10)：1506-1512.

[12]郝雨辰，窦晓波，吴在军，等.微电网分层分布式能量优化管理[J].电力自动化设备，2014，34(1)：154-162.HaoYuchen，DouXiaobo，WuZaijun，etal.Hierarchicalanddistributedoptimizationofenergymanagementformicrogrid[J].ElectricPowerAutomationEquipment，2014，34(1)：154-162.

[13]张丽，徐玉琴，王增平，等.包含分布式电源的配电网无功优化[J].电工技术学报，2011，26(3)：168-174.ZhangLi，XuYuqin，WangZengping，etal.Reactivepoweroptimizationfordistributionsystemwithdistributedgenerators[J].TransactionsofChinaElectrotechnicalSociety，2011，26(3)：168-174.

[14]ErsegheT.DistributedoptimalpowerflowusingADMM[J].IEEETransactionsonPowerSystems，2014，29(5)：2370-2380.

[15]ZhengWeiye，WuWenchuan，ZhangBoming.Afullydistributedreactivepoweroptimizationandcontrolmethodforactivedistributionnetworks[J].IEEETransactionsonSmartGrid，2015，7(2)：1021-1033.

[16]PengQiuyu，LowSH.Distributedoptimalpowerflowalgorithmforbalancedradialdistributionnetworks[J].DOI:10.119/TSG.2016.2546305.

[17]SulcP，BackhausS，ChertkovM.Optimaldistributedcontrolofreactivepowerviathealternatingdirectionmethodofmultipliers[J].IEEETransactionsonEnergyConversion，2014，29(4)：968-977.

[18]Dall′AneseE，ZhuHao，GiannakisGB.Distributedoptimalpowerflowforsmartmicrogrids[J].IEEETransactionsonPowerSystems，2012，4(3)：1464-1475.

[19]GanLingwen，LiNa，TopcuU.Exactconvexrelaxationofoptimalpowerflowinradialnetworks[J].IEEETransactionsonAutomaticControl，2015，60(1)：72-87.

[20]李佩杰，陆镛，白晓清，等.基于交替方向乘子法的动态经济调度分散式优化[J].中国电机工程学报，2015，35(10)：2428-2435.LiPeijie，LuYong，BaiXiaoqing，etal.Decentralizedoptimizationfordynamiceconomicdispatchbasedonalternatingdirectionmethodofmultipliers[J].ProceedingsoftheCSEE，2015，35(10)：2428-2435.

[21]刘斌，刘锋，梅生伟，等.基于二阶锥优化的含有载调压变压器主动配电网最优潮流[J].电力系统自动化，2015，39(19)：40-47.LiuBin，LiuFeng，MeiShengwei，etal.Optimalpowerflowinactivedistributionnetworkswithon-loadtapchangerbasedonsecond-orderconeprogramming[J].AutomationofElectricPowerSystems，2015，39(19)：40-47.

[22]GanLingwen，LowSH.Optimalpowerflowindirectcurrentnetworks[J].IEEETransactionsonPowerSystems，2014，29(6)：2892-2904.

[23]李佩杰，罗翠云，白晓清，等.一种求解多相混合配电网潮流的扩展序分量法[J].电力系统保护与控制，2016，44(3)：15-23.LiPeijie，LuoCuiyun，BaiXiaoqing，etal.Anextendedsequencecomponentsmethodforsolvingmultiphasepowerflowindistributionnetworks[J].PowerSystemProtectionandControl，2016，44(3)：15-23.

[24]LowSH.Convexrelaxationofoptimalpowerflow—partII：exactness[J].IEEETransactionsonControlofNetworkSystems，2014，1(2)：177-189.

[25]欧阳逸风，刘明波.暂态电压安全多目标混合整数最优控制模型及凸松弛方法[J].中国电机工程学报，2015，35(23)：6018-6027.OuyangYifeng，LiuMingbo.Multi-objective/mixed-integeroptimalcontrolmodelandconvexrelaxationmethodfortransientvoltagesecurity[J].ProceedingsoftheCSEE，2015，35(23)：6018-6027.

[26]BoydS，ParikhN，ChuE.Distributedoptimizationandstatisticallearningviathealternatingdirectionmethodofmultipliers[J].FoundationsandTrendsinMachineLearning，2011，3(1)：1-122.

[27]PengQiuyu，LowSH.Distributedalgorithmforoptimalpowerflowonaradialnetwork[C]//53rdIEEEConferenceonDecisionandControl，LosAngeles，USA，2014：167-172.

(编辑 张玉荣)

Distributed Optimal Power Flow in Direct Current Distribution Network Based on Alternative Direction Method of Multipliers with Dynamic Step Size

HanYuxin1ChenLaijun1WangZhaojian1LiuWei2MeiShengwei1

(1.State Key Lab of Control and Simulation of Power Systems and Generation Equipments Department of Electrical Engineering Tsinghua University Beijing 100084 China 2.Shaanxi Regional Electric Power Group Co.Ltd. Xi′an 710061 China)

Direct current distribution network has broad prospects，and its optimal power flow(OPF)problem has important significance to economical operation.Following the advances in second-order cone programming(SOCP)convex optimization，this paper establishes the SOCP-OPF model in which the constraints of voltages，currents and power are considered for direct current distribution network in redial topology.In addition，a distributed OPF calculating method based on alternating direction method of multipliers(ADMM)is proposed to overcome many difficulties faced by traditional centralized dispatch method.Compared with existed researches，each bus is equipped with a computing agent and the agents exchange simple information with neighbors in every iteration，then solve the optimization problem in a parallel pattern without centralized global coordination.The SOCP-OPF model takes the current limits on the lines into consideration，which makes the model more practical.The proposed method also has a dynamic step size adjusting strategy to improve the efficiency of calculating.Numerical simulations on typical system show the good convergence and accuracy of the algorithm.

DC distribution network，distributed optimization，optimal power flow(OPF)，alternating direction method of multipliers(ADMM)，dynamic step size

国家自然科学基金创新研究群体项目(51321005)。

2016-05-12 改稿日期2016-10-04

TM744

韩禹歆 男，1992年生，硕士，研究方向为电力系统分布式优化。

E-mail：hanyuxin1992@126.com

陈来军 男，1984年生，副教授，研究方向为新能源发电与储能技术。

E-mail：chenlaijun@tsinghua.edu.cn(通信作者)