为有源头活水来
康鑫
[摘 要]数学概念的建立是解决数学问题的前提,学生在运用数学概念进行推理、判断后要得出正确的结论,首先要正确地掌握概念、理解概念。以北师大版数学六年级下册“正比例”的教学为例,通过体会概念的发生之源、探究抽象的经验之源、解决问题的应用之源,让学生对数学概念既知其然,又知其所以然。
[关键词]整体认知;丰厚情境;过程抽象;应用之源
[中图分类号] G623.5 [文献标识码] A [文章编号] 1007-9068(2017)17-0025-02
正确理解并灵活运用数学概念,是掌握数学基础知识和运算技能、发展逻辑论证和空间想象能力的前提。而忽略了概念的背景或源头,学生的概念学习如无源之水、无本之木。如何才能从“源头”出发,帮助学生理解数学概念?下面就从北师大版六年级下册“正比例”的教学说起。
一、忌空中楼阁,重知识源头
所谓源头,就是指教学的起源。正、反比例是重要的函数关系,要让学生能够体会函数思想,就需要丰富的教学情境。为此,教材在“正比例”之前安排了“变化的量”,意在拓宽学生理解正、反比例的背景。“正比例”这一课时,教材首先给出了正方形的周长与边长以及面积与边长的表格,让学生研究面积与边长以及周长与边长变化中的相同和不同后,再结合对路程与时间的变量关系的研究,抽象出正比例的意义。不难看出,对于前一课时“变化的量”,学生虽然体会到生活中存在着大量的相互依存的变化的量,但没有对变化量的变化方向进行研究与分类,而“正比例”这一课呈现的只是变化方向一致的变量,没能很好地让学生明晰知识的源头,这样就会对学生后续学习反比例有一定的影响。为了让学生从整体上认知正、反比例,让学生体会知识发生之源是很有必要的。
【片断一】研究变化的量,找相同与不同
课件呈现五个表格的信息。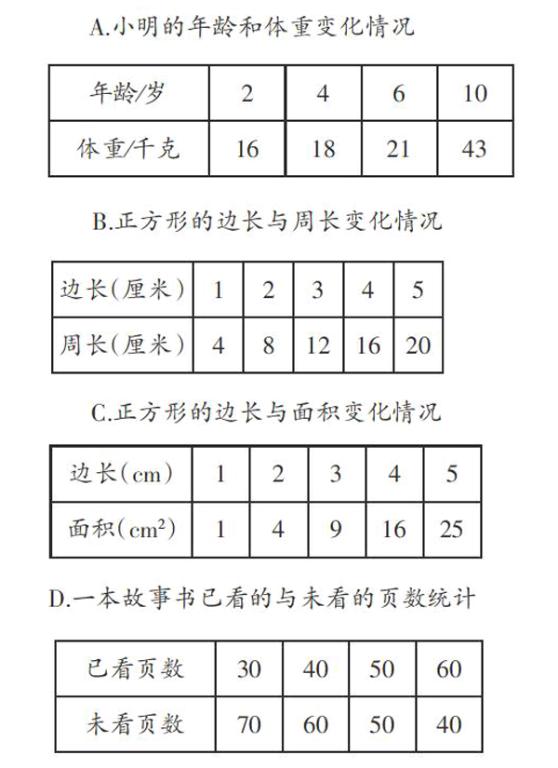
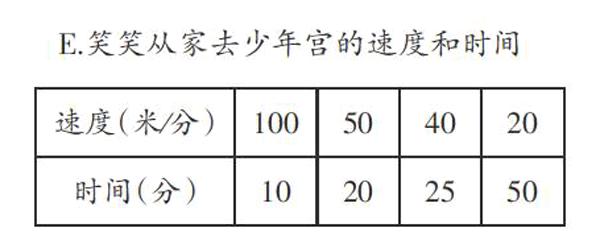
师:上节课我们学习了变化的量,知道研究变化的量可以从三个方面入手,请说说是哪三个方面?
生1:有哪些变化的量。
生2:是怎么变化的。
生3:是怎么描述的。
师:老师又给大家带来了一些变化的量,请你们从这三个方面思考,然后在小组内说一说这些表格中的量有什么相同的地方,又有什么不同的地方。
学生思考后得出:
相同:都有两个变量,一个量变化,另一个量也变化。
不同:变化的情况有的相同,有的不相同。
问题:你能根据变量的变化情况将表A、B、C、D、E进行分类吗?
生4:我们分了三类。一类是表A、B、C,每个表中的两个变量都是“一个量增加,另一个量也随着增加,一个量减少,另一个量也随着减少”;第二类是表D、E,每个表中的变量都是“一个量增加,另一个量反而减少,一个量减少,另一个量反而增加”。
师:大家的意见老师也同意,可以说表A、B、C中两个量的变化方向都是一致的,表D、E中两个量的变化方向都是相反的。今天这节课,我们先来研究变化方向一致的两个量的关系。
学生借助研究“变化的量”获得的经验,在研究五个有代表性的表格信息后,明晰了互相依赖的变化量的变化方向有的是一致的,有的是相反的,体会到变化的量多而复杂,但有规律,体会到本课学习内容源自生活中变化的量,体会到探究的方法来自之前习得的研究经验。
二、忌形式抽象,重过程抽象
概念形成的过程就是抽象的过程。教师要引导学生在操作活动或分析、比较等思维活动中,体会不同材料的共性变化,逐层抽象出概念的共同属性,再通过解释、思辨等学习活动掌握概念的本质。教材在研究“正方形周长与边长、面积与边长的变化规律”后,并未揭示正比例的意义,而是在研究了“路程与时间的变化规律”后,才描述正比例的意义。可见,让学生经历抽象过程的意图是明显的,路径是清晰的,即通过在相同中找不同、不同中找相同,归纳正比例的意义,学习路径是直线形的。为此,教师可在把握正、反比例的整体上,引导学生经历找相同与不同、找不同与相同的数学化过程,进而抽象出正比例的意义。这样的抽象过程更丰厚,更利于学生理解所学概念的本质。与此同时,通过反思总结,学生更能深刻体会到,探究知识的经验之源能为学习后续知识积累丰富的活动经验。
【片断二】研究变化的量,找不同与相同
1.深入分析,找出不同
師:表A、B、C中的两个量变化方向都是一致的,它们的变化有什么不同吗?
学生讨论后得到:
表A中两个量的变化好像没有规律。
表B中周长总是边长的4倍。
表C中面积除以边长的得数不一样。
师(追问):表B中,周长为什么总是边长的4倍?表C中,面积除以边长的得数为什么不固定?
生1:正方形周长等于边长乘4,所以周长与边长的比值一定,而正方形面积等于边长乘边长,面积除以边长等于边长,因为边长在变,所以得数不固定。
2.研究中再感知
一辆汽车以90千米/时的速度行驶,行驶的路程与时间如下所示。把下表填写完整,你能从表中发现什么?
F.汽车行驶的路程与时间的变化情况
学生独立填表后交流。
生2:路程随时间变化而变化,变化方向相同,而且路程与时间的比值一定,也就是速度一定。
3.比较中找相同,揭示意义
师:比较表F和表B中变量的变化情况,有什么相同的地方?
生3:都有两个变量,变化方向一致,两个变量的比值都是一定的(不变的)。
师:像这样的两个量的关系就是正比例关系,这样的两个量成正比例。
4.解释变化的量,建构意义
师:周长和边长成正比例吗?为什么?表F的路程和时间成正比例吗?为什么?正方形面积和边长成正比例吗?为什么?怎样的两个量成正比例?
师(归纳):两个变量如果变化方向一致,比值一定,它们就是正比例关系。
师:你是怎样理解这里“正”的意思的?这里的“比例”在哪能找到?
生4:“正”就是变化方向一致,比例有很多,比如表B中,4∶1=8∶2,8∶2=16∶4,1∶4=2∶8,1∶2=4∶8。
5.回顾反思,积累研究经验
师:我们是怎样研究正比例关系的?
生5:先分析变量的变化规律,然后通过比较找出它们的相同之处。
学生通过研究变化方向一致的变量的变化规律,经历了五个层次的学习思维活动后,逐步抽象出正比例的意义,体会到概念的抽象性。
三、忌偏重技能,重内化理解
数学概念形成的核心是理解。教材的第一课时安排了两道练习题,这两道练习题都是通过表格呈现两个变量的几组对应的数据,让学生判断两个量是否成正比例,并说出原因。其用意是让学生通过在具体情境中的判断进一步理解正比例的意义,而不是急于落实技能目标。由于正比例知识属于主观性知识范畴,让学生经历知识的形成过程、理解知识的本质尤为重要,但体会知识产生的必要性不可或缺。只有明白了知识在哪里用、怎么用,学生对概念的本质才能做到真正理解,才有利于学生数学素养的形成与发展。因此,概念课的教學既要设计帮助学生内化理解的练习,也要设计源自生活的问题,让学生切实体会学习的价值。
【片断三】练习应用,内化本质
师:我们已经理解了正比例关系,现在来解决一些问题吧!
1.学校科学小组在同一时间、同一地点进行观察实验,测得竹竿的高与竹竿的影长如下表所示:
(1)说一说竹竿的影长与竹竿的高的变化关系。
(2)写出竹竿的影长与竹竿的高的比,有什么发现?
(3)竹竿的高与竹竿的影长是不是成正比例?为什么?
2.出示PPT:
学生阅读、思考、讨论、交流。
学生观察后能够发现同时同地竹竿的高和竹竿的影长的关系,再次理解了正比例的意义,为反比例的学习与研究打下了坚实的基础。在解释与探究测量金字塔高度的原理与方法的过程中,学生能感悟学习正比例的必要性,体会数学知识的应用之源,达到了对正比例既知其然,更知其所以然的教学效果。
(责编 童 夏)

