极化调制在卫星通信中的应用

张晓凯，郭道省，张邦宁，刘芳君，王耀文

(解放军理工大学 通信工程学院，江苏 南京 210007)



极化调制在卫星通信中的应用

张晓凯，郭道省，张邦宁，刘芳君，王耀文

(解放军理工大学 通信工程学院，江苏 南京 210007)

通过对电磁波极化特性的分析，提出基于极化调制的卫星通信体制，并针对极化调制特点设计出相应的收发信机，推导了高斯信道下极化调制的误符号率理论公式，并使用蒙特卡洛仿真进行了验证。同时，证明了极化调制不受高功放的非线性影响且不需要严格载波同步，在无精确载波同步的条件下极化调制误符号率性能优于DPSK非相干解调的性能，得出极化调制更适用于高频窄带或者高动态等卫星通信系统。

极化特性；极化调制；DPSK；载波不同步；卫星通信

0 引言

随着卫星通信的发展，卫星的数量急剧增加，只有不断开发更高频段[1]以避免相互干扰。但随着载波频率提高，同步复杂度越来越高，建立时间也越来越长。在传统的窄带高频或者高动态卫星通信中，建立精确的载波同步所需代价非常高，因而采用差分相位调制(DPSK)及其非相干解调来满足非精确载波同步情况下的通信需求[2]。

极化作为电磁波的重要特征已被广泛应用于雷达[3]、光纤[4-5]和卫星通信中，对电磁波极化特性的充分利用可以为无线网络容量提升[6]、能耗降低[7]、异构网络共存[8]等问题提供新思路。例如在传统卫星通信中，利用正交的两路极化状态将频带利用率提升一倍[9]。在光纤通信中，通过光的不同偏振状态来承载信息[4-5]，称为偏正键控调制(Polarization Shift Keying, PolSK)。随着极化理论的不断发展，国内外很多学者受PolSK调制的启发，已经将极化状态用于承载信息，称为极化调制(Polarization Modulation, PM)。例如Cao Bin[10]受雷达信号处理启发，最先提出在视距传输(Line of Sight，LoS)下的极化调制的可行性，但并未给出合理的系统设计以及理论误码率的推导。Wei Dong[6-7,11-12]提出一种极化幅度联合(Polarization Amplitude Modulation, PAM)调制的方法，该方法从能效角度分析，将极化调制与传统调制联合实现功率利用率的提升。Li Ruomeng[13]以提升频谱效率为目标提出一种连续极化调制的方法。目前极化调制主要研究集中于地面无线通信，且处于起步阶段。

在卫星通信系统中，由于其信道环境相对较好，天线系统具有非常好的方向性和极化识别特性，加之星上数字信号处理能力的提高，都为极化调制在卫星上的应用提供了基础。

1 星通信中极化调制方案

卫星信道与地面无线信道具有较大的差别，其主要的特点是白噪声信道、长延时、功率和频带受限。

1.1 极化的表征以及快速变极化信号产生

从极化角度出发，电磁波可以分为完全极化波、部分极化波和未极化波。一般在无线电传输过程中，由于去极化效应，通常为部分极化波，为了便于表示，采用完全极化波表示[10]。对于完全极化波通常的极化描述[14]有电磁波的Jones电场矢量E、复极化比ρ、极化椭圆几何描述子(ε,τ)、极化相位描述子(δ,φ)以及Stokes矢量J。Jones矢量选定任意一组正交的极化(H,V)作为一组基，用电场表示交变电磁场即可，所以有E=EhH+EvV，E=[Eh,Ev]T,则Jones矢量与极化相位描述子表示为[15]：

(1)

图1 在Poincare上相位描述子与几何描述子

其中，δ称为极化辅角，取值范围为[-π/2,π/2]，φ称为极化相位差，取值范围为[-π,π]。George Stokes引入Stokes矢量更加形象地描述极化状态，在功率密度一定时，选择g1、g2和g3作为一组三维的正交基。为了在球坐标下便于描述，采用方位角和仰角表示极化椭圆几何描述(ε,τ)。在归一化功率下，Jones矢量、Stokes矢量和几何描述子通过坐标变换都可以映射在Poincare极化球面上，如图1所示。

目前主要的快速变极化技术主要有变更馈线内电磁波模式的变极化装置天线的基于硬件的变极化和虚拟极化自适应技术[14](Virtual Polarization Adaptive, VPA)。VPA技术利用双正交极化通道，对两个通道进行幅度和相位加权的数字信号处理，然后分别馈给极化正交天线或者一根双极化天线，即可在空间中形成任意极化状态的电磁波。由于VPA技术具有较高的灵活性，其为任意状态的极化电磁波的快速实现提供了基础。

1.2 星座图映射

由于极化状态分布在Poincare球表面，所以将极化调制推广至高阶时，考虑到抗衰落和提升频谱效率的前提下，高阶调制必须满足恒包络、星座之间等间距且中心对称分布，则2、4、8和16进制星座图如图2所示。

图2 PM星座图

1.3 极化调制收发信机设计

在传统的收发信机的基础上，利用功分和相移单元将极化信息调制到相互正交极化天线上。PM发射机原理如图3所示。

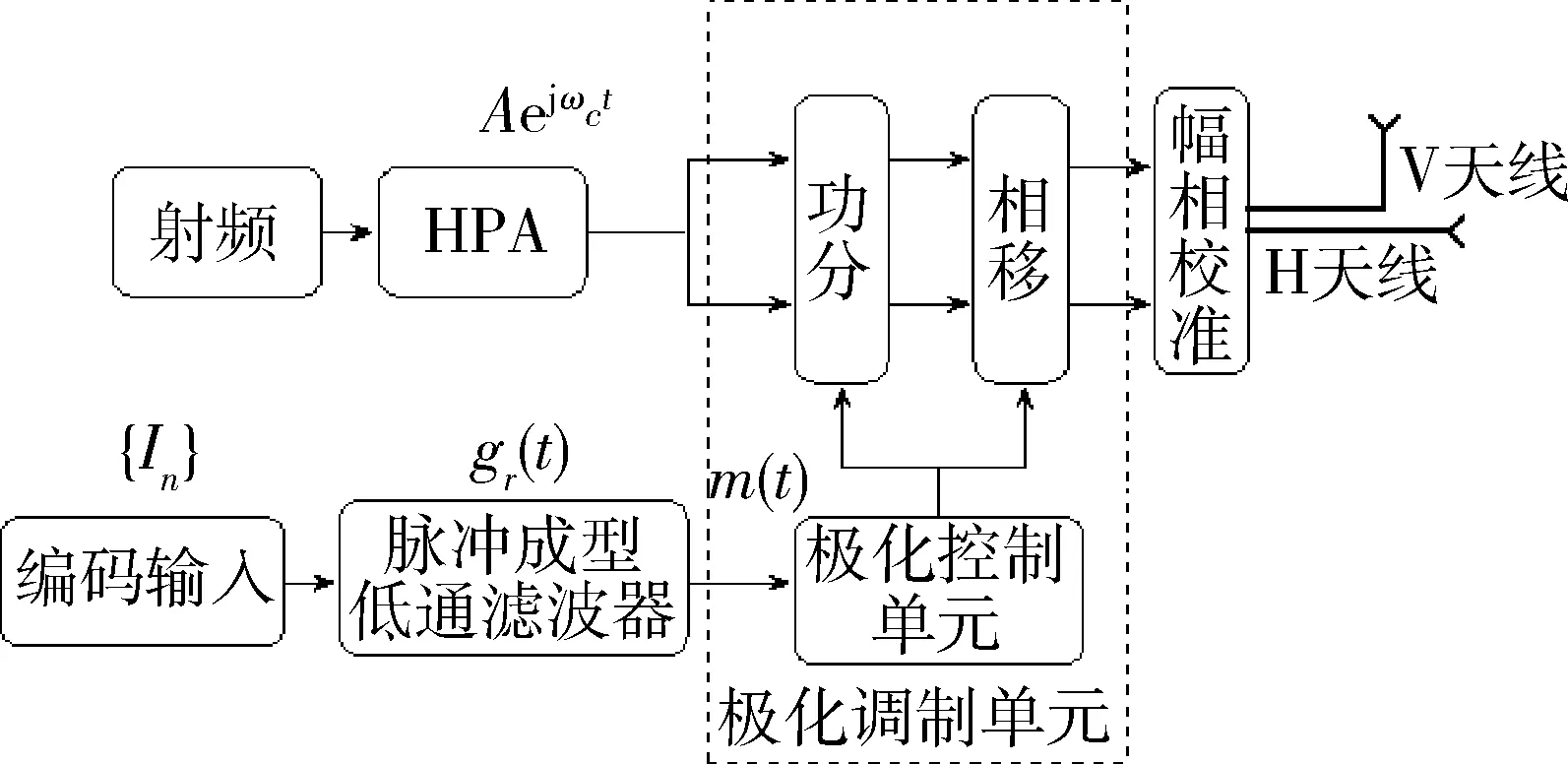
图3 极化发射机

在信息比特序列经过脉冲成型滤波之后，极化映射单元根据极化星座图映射，产生对应的符号映射为极化描述子(δi,φi)，其功分单元系数为G=[cosδi0; 0 sinδi], 相移单元系数为：F=[1 0; 0 ejφi]，经过变换后的信号为：

(2)

调制后的信号经过幅相校准后，使用双正交将信号发出，在卫星信道下，通常选取相互正交的左旋和右旋圆极化状态或者垂直和水平极化。

为了从载波中恢复出发射信息，设计基于Stocks矢量的PM接收机，如图4所示。

图4 极化接收机

两路天线信号经过下变频、采样和幅相校准之后，利用ERH和ERV，得到接收极化信号ER的Stocks矢量：

(3)

其中φR=φRV-φRH，将stocks矢量归一化到单位Poincare球面上，通过最大似然判决(Maximum Likelihood Decision, ML)，即计算接收到极化状态ER与原始星座点Ei(i=1,2，…，M)距离之间的球面距离li，最小球面距离对应的原始星座点即判决为发送信息。如图5所示，在4PM判决中，l1要小于l2,l3,l4，则该符号判决为E1。

图5 PM最大似然判决示意图

1.4 卫星通信信道模型

在卫星信道下， LoS为信号主要成分，对于卫星通信系统有ER=H·E+η,其中ER代表接收信号，E为发射信号，H表示信道参数，η为高斯白噪声。

VPA采用双正交天线实现，则该卫星信道等效为2x2MIMO信道，则极化对角信道模型为[16]：

1.5 AWGN信道下PM性能

在AWGN信道下，高斯噪声使得极化状态在Poincare球上所对应的点上发生偏移，所以在判决时，将按照各星座点为中心，平均将Poincare球分割成若干判决区域，在某一个点的判决域如图6所示，其为8PM某一星座点正视图，其中dis0为相邻星座点的一半，disij为第i个星座点与其判决区域中第j个端点之间的球面距离。其中，α(dis,θ)=2arccos(tandis/tanθ)。

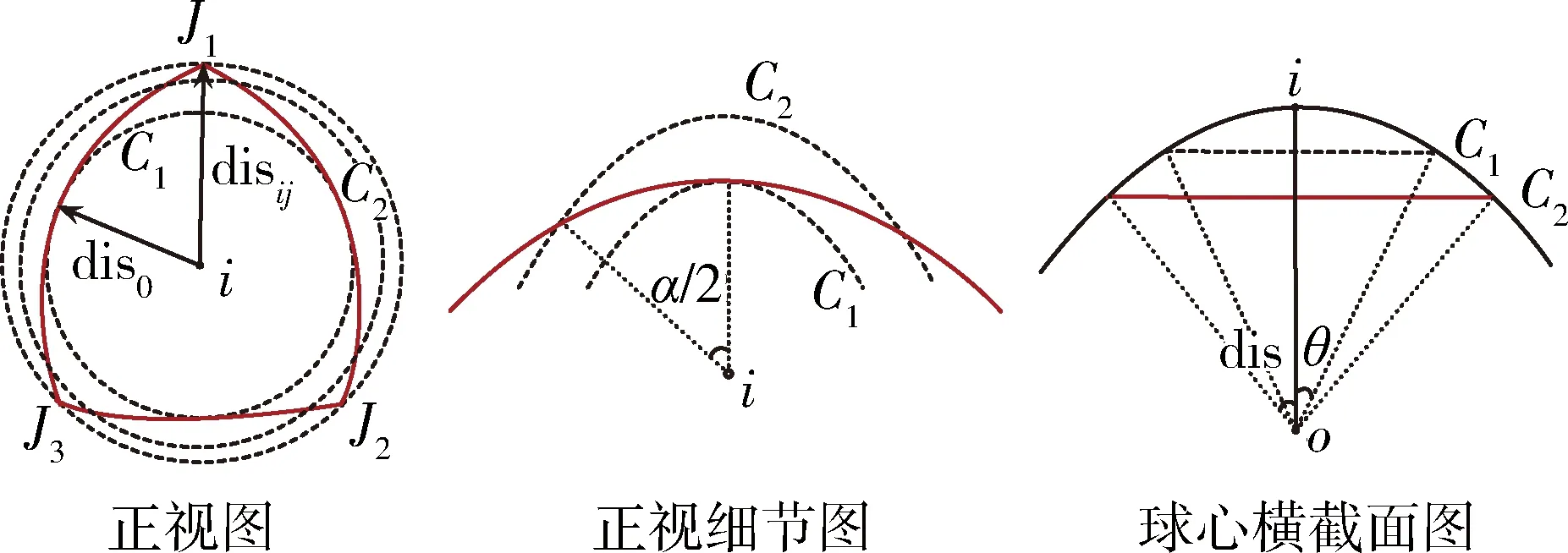
图6 8PM某星座点判决域

定义PM信号的接收信噪比(Receive Signal to Noise Radio, RSNR)为RSNR=P/σ2，P为接收功率，σ2为高斯噪声平均功率，则接收信号在Poincare球上关于RSNR的几何极化描述子的联合分布为[4]:

(5)

(6)

2 极化调制仿真结果与分析

PM理论误符号率由式(6)可知，使用MATLAB软件对2PM、4PM、8PM和16PM的理论误符号率进行仿真，如图7所示。

图7 MPM与DPSK非相干解调误符号率

在AWGN信道条件下，对4PM进行蒙特卡洛仿真。在MATLAB软件中，发送比特序列长度设置为1 000 000，将每2 bit映射为一个符号，经过AWGN信道，采用最大似然接收的方式，统计RSNR在10～20 dB条件下误符号率如图8所示。

图8 4PM理论误符号率与蒙特卡洛仿真

通过与4PM理论值进行比较，蒙特卡洛仿真曲线与理论曲线在一定误差范围内保持一致。误差主要是由于在文献[4]中，接收的概率分布将一阶贝塞尔函数进行了近似。图7充分说明PM中对误码率的推导在实际中具有指导意义。然而单纯的极化调制与传统的PSK、FSK相比，在相同的接收信噪比条件下，其误码率性能并没有明显的优势。但PM通信系统中，由于计算接收Stocks矢量gR1，gR2和gR3采用的是两路信号的幅度和相对相位，下变频时，并不需要精确估计出载波频率，只要信号能够通过下变频之后的滤波器即可。所以极化调制适用于载波同步较为困难的场景，例如高频窄带卫星通信系统或者高动态等。所以将PM与2DPSK非相干解调的误符号曲线进行比较，如图7所示。

由图7可以看出2PM与2DPSK误符号率几乎一致；4PM与4DPSK相比，在相同的误符号概率下，信噪比需要高3 dB左右；当调制的阶数增加，8PM和16PM的误码率性能明显优于8DPSK和16DPSK。

卫星通信系统中，在射频前端会经过一个高功率放大器(High Power Amplifier, HPA)，由于放大器非线性，在DPSK等传统调制方式下需要进行功率回退。

卫星下行链路的表达式为：

(7)

其中C/N0为载噪比，EIRP为卫星有效全向辐射功率，G/T为接收端天线的增益噪声比，L为传输损耗，BO为发射端为满足信号非线性失真设置的功率回退。

在图3设计极化调制发射机中，极化调制可以直接在HPA之后。功放的非线性会产生交调干扰分量，可能会出现多阶交调，交调分量之间又产生相互交调，产生更多的交调信号，所以基带信号经过放大器之后可以表示为：

(8)

其中，E为多个交调分量和原始分量的混合信号，每个信号都经历过不同的幅度和相位失真，N为E的分量数，Ak、θk分别为每个fk频率分量的幅值和相位。其通过极化映射单元F、G之后，有:

(9)

在接收端ER的相位描述子(δE,φE)为：

(10)

由式(10)可以得出，带有极化信息的信号，在经过非线性放大器交调的前后不发生改变，所以PM承载的信息不受功放的非线性影响。则采用PM该卫星通信系统中，在卫星本身功率允许的条件下，可以不需要设置功率回退。

当DPSK与PM系统在相同的噪声环境下，DPSK需要设置功率回退(在卫星放大器中BO一般为6 dB)，而极化调制不设置。在星上功率允许的条件下，由图7可以看出，2PM误码率性能将比2DPSK优大约6 dB。4PM在高斯白噪声下，只比4DPSK性能差约3 dB，从这个角度出发， PM的调制性能远远优于DPSK。另外，在接收端φE是通过两正交信号相位差，这也使得PM调制能够很好地克服相位噪声的影响。

3 结论

本文提出了一种极化调制的方法，由于其不受卫星放大器的非线性影响，不需要严格的载波同步，所以可以有效克服相位噪声而更加适用于高频窄带卫星系统、高动态等卫星通信系统。但是由于调制在HPA之后，对硬件的要求较高,另外由于采用VPA技术，正交的两种极化状态在传输过程中会出现极化模式色散和极化相关损耗等去极化效应，所以在下一步研究中，需要加以考虑。

[1] AREND L, SPERBER R, MARSO M, et al. Implementing polarization shift keying over satellite-system design and measurement results[J]. International Journal of Satellite Communications and Networking, 2016, 34(2):211-229.

[2] LEIB H. Data-aided noncoherent demodulation of DPSK[J]. Communications IEEE Transactions on, 1995, 43(234):722-725.

[3] 贺峰. 宽带/超宽带雷达运动人体目标检测与特征提取关键技术研究[D]. 长沙：国防科学技术大学, 2011.

[4] BENEDETTO S, POGGIOLINI P. Theory of polarization shift keying modulation[J]. IEEE Transactions on Communications, 1992, 40(4):708-721.

[5] BENEDETTO S, POGGIOLINI P T. Multilevel polarization shift keying: optimum receiver structure and performance evaluation[J]. Communications IEEE Transactions on, 1994, 42(234):1174-1186.

[6] Wei Dong, Feng Chunyan, Guo Caili. An optimal pre-compensation based joint polarization-amplitude-phase modulation scheme for the power amplifier energy efficiency improvement[C]. IEEE International Conference on Communications. IEEE, 2013:4137-4142.

[7] Wei Dong, Feng Chunyan, Guo Caili. An energy efficient subcarrier-power allocation scheme for polarization-amplitude-phase modulation in channel with polarization mode dispersion[C]. Wireless Communications and Networking Conference, IEEE, 2013:580-585.

[8] Guo Caili, Wu Xiaobin, Feng Chunyan, et al. Spectrum sensing for cognitive radios based on directional statistics of polarization vectors [J]. IEEE Journal on Selected Areas in Communications, 2013, 31(3): 379-393.

[9] WU J, WU M C. Dual-polarization frequency reuse with frequency band shifting allocation[J]. IEEE Transactions on Vehicular Technology, 2000, 49(6):2244-2256.

[10] Cao Bin, Zhang Qinyu, Lin Jin. Polarization division multiple access with polarization modulation for LOS wireless communications[J]. EURASIP Journal on Wireless Communications and Networking, 2011, 2011(1):1-9.

[11] Wei Dong, Zhang Meng, Fan Wei, et al. A spectrum efficient polarized OFDM scheme for wireless depolarized channel[C]. IEEE Computer Society, 2015:649-656.

[12] Wei Dong, Feng Chunyan, Guo Caili, et al. A power amplifier energy efficient polarization modulation scheme based on the optimal pre-compensation[J]. IEEE Communications Letters, 2013, 17(3):513-516.

[13] Li Ruomeng, Liu Fangfang, Zeng Zhimin. A m-continuous polarization modulation scheme for improving the bandwidth efficiency[C]. 17th International Symposium on Wireless Personal Multimedia Communications(WPMC2014), 2014: 253-258.

[14] Guo Caili, Liu Fangfan, Chen Shuo, et al. Advances on exploiting polarization in wireless communications: channels, technologies, and applications[J]. IEEE Commun. Surveys and Tutorials, 2017, 19(1):125-166.

[15] 王雪松.宽带极化信息处理的研究[D].长沙：国防科学技术大学,1999.

[16] LIOLIS K P, VILARDEBO J G, CASINI E. Statistical modeling of dual-polarized MIMO land mobile satellite channels[J]. IEEE Transactions on Communications, 2010, 58(11):3077-3083.

[17] DEGLI-ESPOSTI V, KOLMONEN V, VITUCCI E M, et al. Analysis and modeling on co- and cross-polarized urban radio propagation for dual-polarized MIMO wireless systems[J]. IEEE Transactions on Antennas & Propagation, 2011, 59(11):4247-4256.

[18] 代大海, 王雪松, 肖顺平,等. 电磁波极化变换的数学原理及其性质[J]. 中国科学，2008, 38(10):1301-1311.

The application of polarization modulation in satellite communication

Zhang Xiaokai, Guo Daoxing, Zhang Bangning, Liu Fangjun, Wang Yaowen

(College of Communication Engineering, PLA University of Science and Technology, Nanjing 210007, China)

Based on the analysis of electromagnetic wave polarization characteristics, the polarization modulation (PM) scheme is proposed and the PM transceiver is designed in the satellite communication in this paper. The symbol error rate of the polarization modulation is deduced and verified by the Monte Carlo simulation in the AWGN channel. It is proved that the polarization modulation does not require accurate carrier synchronization and transmit signals are immune to nonlinearity of the high power amplifier. Comparing with the DPSK non-coherent demodulation, PM scheme is more suitable in no carrier recovery systems, such as high frequency narrow-band or high dynamic satellite communication.

polarization feature; polarization modulation; DPSK; no carrier synchronization; satellite communication

TN927

A

10.19358/j.issn.1674- 7720.2017.11.020

张晓凯，郭道省，张邦宁，等.极化调制在卫星通信中的应用[J].微型机与应用，2017,36(11)：66-70.

2016-12-06)

张晓凯(1992-)，男，硕士研究生，主要研究方向：电磁波极化信息处理。

郭道省(1973-)，男，博士，教授，主要研究方向：卫星通信、通信抗干扰。

张邦宁(1963-)，通信作者，男，硕士，教授，主要研究方向：卫星通信、通信抗干扰。E-mail:rgsc2014@126.com。