大跨度拱桥静动力试验与结构识别的实践

周云，张军凯，陈松柏，易伟建,2

(1.湖南大学 土木工程学院, 湖南 长沙 410082; 2. 工程结构损伤诊断湖南省重点实验室 湖南大学，湖南 长沙 410082)



大跨度拱桥静动力试验与结构识别的实践

由于有限元建模中存在不确定性因素的影响，大跨度拱桥初始设计模型的理论分析结果与现场测试数据之间存在一定差异.为了消除模型校验技术中的认知不确定性和随机不确定性，从而更好地进行结构识别，本文以来华大桥和巴溪洲大桥为例，对其中若干关键问题进行了讨论.通过合理地现场勘察与精确的有限元模拟相结合，基于灵敏度分析方法进行不确定性参数筛选，并最终采用最小二乘法进行参数优化，实现了可靠的结构工作状况评估与响应预测.研究包括现场静动力试验、有限元模拟、模型校验、响应预测和校验合理性评估等.基于精确建模和模态参数的校验技术可以有效地减小有限元模型与现场静动力试验结果之间的误差，使用未经试验结果校验的设计模型，进行两座桥梁校验系数的评估，分别存在着21%和23%的误差．

模型校验；大跨度拱桥；静动力试验；工作模态分析；结构识别

在大跨度桥梁结构中，拱桥具有跨越能力大、自重轻、外形美观等优点[1].然而，由于拱桥是以推力为主的结构，其施工质量难以控制，且构件的性能变化难以观测[2].大跨度拱桥的构件参数存在一定的不确定性，对其进行状态评估的难度较大.通过结构识别技术确定其真实工作状况，对桥梁的使用、维护、评估以及决策支持具有重要意义.随着结构识别理论在工程领域应用的进展，国内外许多学者对大跨度拱桥的静动力试验和结构识别进行了大量的研究工作.

1997年，Nazmy等[3]探讨了不同设计参数下钢拱桥结构性能的变化，分析参数变化对拱桥的强度和稳定性的影响，并提出了拱桥的结构设计优化建议.2004年，Ren等[4]对田纳西河桥进行了环境振动测试，并分别使用峰值提取法(PP)和随机子空间识别法(SSI)进行了参数识别.2006年，Giovanna等[5]对比进行了MRWA bridge no.3014 使用碳纤维复合材料加固前后的模态测试，在工作模态分析的基础上通过模型修正对结构工作状况进行了评估.2008年，Filipe[6]研究了一种“多通道动态监测系统”，该系统能够实现桥梁的固有频率与频率域分解方法的在线自动识别.2008年，Song等[7]使用密布的无线传感器完成了厦门五缘大桥的模态试验和工作模态分析.2011年，Wei等[8]对一座5跨连续拱桥进行了环境振动测试，结合车桥耦合振动试验以及静载测试的结果，对桥梁的健康状况进行了评估.2011年，Qin等[9]研究了结构识别中各种不确定性因素的来源，并且通过对Henry Hudson桥的结构识别和模型校验实例说明了如何减小不确定性因素对识别结果的影响.2013年，李晰等[10]利用设置在一座钢管混凝土拱桥上的健康监测系统，对实际结构的工作模态进行识别并采用零阶近似法对初始有限元模型进行了修正.2014年，胡志坚等[11]针对九江长江大桥主桥三联拱桥部分开展大缩尺比的静动力模型试验研究，通过各类构件不同的损伤模拟方法研究了结构动力特性的变化.2014年，Costa等[12]对比了路易斯一世桥加固前后随机振动试验的模态分析结果.结合有限元模型结构识别，论证了桥梁刚度、模态参数和边界条件之间的关系.2014年，陈清军等[13]以一座经历地震后的框架结构为研究对象，通过环境振动测试，采用小波变换的方法进行了损伤识别研究.2015年，周云等[14]通过对一块钢-混凝土组合板进行静动力试验，基于脉冲锤击测试的模态柔度理论进行了结构损伤的识别.

基于灵敏度分析的模型校验是依据有限元模型解析解和实验数据之间差异建立目标函数，通过目标函数的优化实现参数识别.由于不确定性参数和模态参数之间的非线性关系，参数修正通常采用迭代算法，识别结果可以保证模型单元的连续性和系统矩阵的物理意义[15-16].

本文以两座新建的大跨度拱桥为研究对象，依据工作模态分析测试结果和有限元计算模态分析结果建立目标函数.通过模型校验技术，最终得到能够真实准确地反映结构状况的有限元校验模型.静载试验结果和校验系数表明，经过现场观测、环境振动试验和模型校验，校验模型能够更准确地模拟实际结构，其响应预测结果更加准确可靠.

1 桥梁结构识别

结构识别理论的提出始于20世纪60年代末.结构识别的范式最早于1977年被Hart和Yao[17]提出.自1978年，Liu和Yao[18]将其引入到土木工程领域后，结构识别成为了工程力学界和土木工程界的一个富有活力的研究方向.2005年，结构识别的概念被ASCE St-Id of Constructed Systems Committee所接受，其范式被描述为“理论-试验-决策”的6步综合圆[19]，如图1所示.

为保证研究工作的缜密和完善，本文的大跨度桥梁结构识别严格按照6步圆的顺序开展.具体工作内容划分如下：

图1 结构识别6步圆

1)观察和概念.详细查阅结构的图纸记录，并结合现场观测结果确定结构的建筑材料、结构形式等，明确结构当前状况和可能出现的损伤.

2)先验模型.基于已知信息建立初始的有限元模型.先验模型相对于实际结构的准确程度可以通过对比其预测结果和现场测试数据来判定.通常可取用设计单位出具的设计模型作为先验模型.

3)控制试验.根据校验目标选定合适的测试方案.对于初始建成的大跨度拱桥，在通车之前对其进行静载试验和随机振动模态试验是有效评定其工作状况的方法之一.静载卡车试验按照预先设定的加载工况使用卡车施加荷载，待加载稳定，观测桥面和拱肋控制截面的应力与变形来判断桥梁结构的受力性能是否满足要求.随机振动试验以环境振动作为激励，通过安放于结构上的单轴加速度传感器拾取结构振动的时域信号.试验测点分为参考点与移动测点，并假定参考点输入信号为高斯白噪声.

4)数据分析与阐述.静载试验[18]主要测试桥梁控制截面的应变、应力和挠度，通过结构在外荷载作用下的反应来评估结构能否达到正常使用的要求.模态试验中，根据各测点的加速度时程信号，经由快速傅里叶变换转换为频域信号.分别计算参考点的自功率谱以及参考点关于各移动测点的互功率谱，最终由PolyMax方法求解结构的模态频率、阻尼与振型.

5)模型校验与参数识别，也称模型-试验匹配.在结构识别的第5步模型校验前，首先要判断有限元模型的准确性，在精确建模并消除有限元模型不合理的模拟方式引入的误差的基础上进行参数识别[20].基于灵敏度分析的参数校验有助于明确对结构响应较为敏感的建模不确定参数并通过目标函数迭代寻优的方法实现参数校验[21].其中，目标函数和不确定参数的选取决定了修正的方向，本文选取了基于模态频率误差的目标函数：

(1)

式中：fai为有限元模型计算所得到的模态频率；fei为实际测试分析得到的模态频率；x为有限元模型中的建模不确定参数；i为所选取的参与目标函数的第i阶模态.

其中，试验模态分析与理论模态分析通过模态置信准则(MAC)匹配(如式(2)所示).MAC值接近于1说明两种振型匹配良好.

(2)

式中：φai和φei分别表示有限元理论模态分析和环境振动测试工作模态分析得到的振型向量；i为进行分析的第i阶模态.

6)结构响应预测.在结构识别第6步，校验系数η[22]是评定结构工作状态和变形性能的一个重要指标，可以由其判定有限元模型的准确程度.η由静载试验数据(应力、挠度)与有限元模型预测结果(应力、挠度)的比值得到，如式(3)所示．

(3)

式中：De,Dr分别表示有限元模型预测的理论挠度与实际结构现场测试挠度.通常，η≤1说明有限元计算结果偏于安全，实际结构工作状况良好并有一定的安全储备.η=1则说明有限元计算结果与试验结果十分接近，模型较为准确地模拟了真实结构.

2 来华大桥结构识别的研究

2.1 桥梁概况

广西来华大桥位于广西省来宾市，是一座中承式钢管混凝土拱桥.大桥全长465 m，桥面宽36 m，主跨拱肋为双肋悬链线无铰拱，计算跨径为220 m，计算拱高60 m，矢跨比为1/3.5.每片拱肋由4根直径750 mm，厚度为20 mm的Q345C钢管组成，内部灌注C50微膨胀混凝土.拱肋之间由水平联通钢管和斜腹钢管连接，整体结构形成桁架式拱肋.桥面板与钢管混凝土拱由立柱和吊杆连接，桥面上下游方向各有8根立柱，21根吊杆，实际结构照片见图2.湖南大学土木工程结构健康监测研究团队(www.hnutest.com)于2013年6月对该桥进行了系统的静动力试验.

图2 来华大桥照片

2.2 静载试验

在各种不同的荷载组合作用下，钢管混凝土拱和主跨桥面竖向变形及应变是本次静载试验的主要内容.加载的位置主要集中在主跨1/2位置和主跨1/4位置.按照不同的车辆数分别设置沿桥梁纵轴对称加载和偏心加载的两种加载形式，每台加载车辆的重量均为300 kN.来华大桥静载试验共预设了20个加载工况，其中主跨1/4位置加载10台车的工况如图3所示.

图3 静载试验加载布置图

桥面测点布置在沿桥面均匀分布的8等分点上，位于桥面防撞护栏内侧平坦处.测试过程采用电子水准仪和光学人工水准仪分别进行测量读数，并相互校核测试结果.在进行钢管拱的静载卡车试验前，预先将全站仪棱镜安放在钢管拱上各个8等分点位置，分别在上下游河滩安置全站仪测量各个测点的位移结果.

2.3 模态试验

本文使用LMS Cadax-8系统进行数据采集，3个参考点(第4#，11#和16#测点，可见图4的传感器固定布置，每次测试移动其余5个传感器所测试的位置.测试过程：首先将传感器竖直放置，拾取竖向的加速度时程响应，然后将传感器水平放置，完成桥梁横向振动测试．数据采集时间为10～20 min，采样频率为512 Hz．由随机子空间识别法获得的桥面竖向振动稳态图见图5.

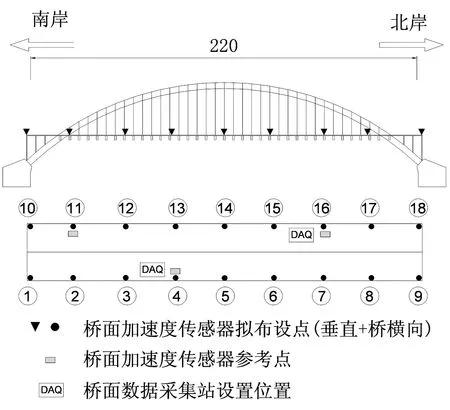
图4 来华大桥模态测试测点布置图

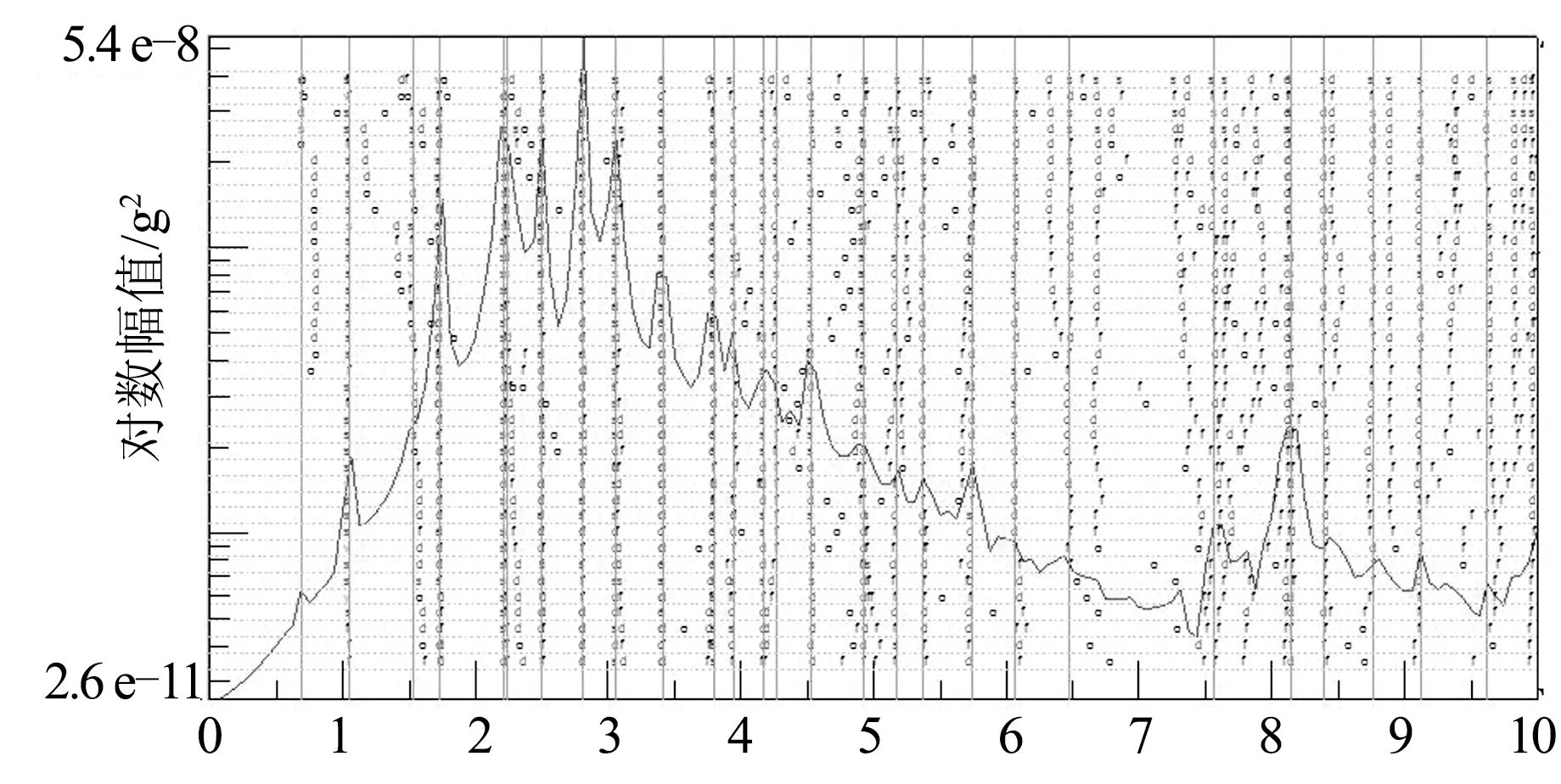
频率/Hz

2.4 有限元建模及分析

根据来华大桥在设计和成桥试验的两个阶段的研究目的，笔者分别使用有限元软件Midas Civil和Strand7建立了来华大桥的空间有限元模型(后文分别以设计模型和校验模型指代)，从模型校验前后所得到的不同结果可以预测实际结构和计算模型在性能方面的差异.

来华大桥设计模型通过Midas建立(图6)，根据其进行全桥施工过程控制，各个施工阶段的线型和应力都在合理的范围内.主要控制参数能直观地反映实际工作状况，相应的有限元计算结果可以作为成桥静动力试验的有力参考.

在完成静载控制试验和模态测试后，笔者使用Strand7建立了来华大桥校验模型(图7).所有单元的几何特征和物理参数都详细按照现场勘测结果确定.拱肋、纵梁和横梁、K型横撑、立柱等均使用两节点的beam单元模拟；拉索的模拟使用仅承受拉力的三维cable单元；桥面板、人行道板和人行道扶手由plate单元模拟.桥面板两端与引桥部分通过伸缩缝隔开，其边界条件在有限元模型中被模拟为理想铰支座(限制相应节点的纵、横向和竖向平动位移).钢拱的两端边界条件假定为固定约束(限制相应位置节点的全部平动及转动位移).

3）提升设施设备维修维护水平。实验室设施设备是保护人、财、物、数据、环境等的重要屏障，提升维修维护水平，有利于大大降低安全风险。可以通过以下方式：第一，单位自己组建专业化的运维团队；第二，招标专业化公司统一代为运维，可采取全包和部分外包的形式；第三，按照谁使用谁负责的原则，由使用方运维管理。不论采取何种方式还需单位指定部门做好监督工作，保证实验室设施设备及时得到维修维护，且工况良好。

图7 经过校验的有限元模型

灵敏度分析反映模型输出的分析结果对各建模参数的敏感程度.通常，在有限元模型中选取主要单元的弹性模量、几何尺寸以及边界条件为不确定性参数.不确定参数是模型校验中的自变量，校验结果通过改变参数的数值实现，每个不确定性参数的上下限定义了修正参数的变化范围，即模型校验的约束条件.校验结果在缩小模型与真实结构之间误差的前提下，首先应保证校验后的不确定性参数具备现实物理意义[23].另外参数变化范围也根据工程经验、施工工艺和相关参考文献的常用取值范围选取[24]，本文对每个不确定性参数选取的合理约束界限统计见表1.来华大桥部分不确定性参数的基于模态参数的灵敏度分析结果见图8.其中，横轴为不确定性参数的标准化弹性模量，竖轴为基于7阶模态频率的目标函数值，见式(2).根据灵敏度分析结果，选取4个对模态分析结果有显著影响的关键不确定性参数为目标函数中待修正的自变量，将工作模态分析结果最可靠的前7阶模态频率选为修正参数(即n=7)，通过调整不确定参数的取值寻找有限元模态分析结果与工作模态分析结果前7阶频率相对误差的迭代寻优.目标函数迭代优化过程中，通过式(3)实现有限元计算模态与试验模态振型的匹配，并定义自变量的约束条件为：

lb≤x≤ub

(4)

式中：x,lb,ub分别表示不确定参数、变量下限和变量上限.本文采用有限元软件Strand7的API模块实现其与Matlab的交互访问，并使用最小二乘迭代优化算法lsqnonlin进行校验，收敛准则为：

abs(fi+1-fi)≤1.0×10-3或iter≥50

(5)

abs(fi+1-fi)与iter分别表示相邻两次迭代运算目标函数的差值和当前迭代次数，所有参数的校验结果统计见表1.

标准化弹性模量

参数设计参数/104变量下界变量上界校验结果/104混凝土拱弹性模量/MPa4.400.60E11.50E13.06钢拱弹性模量/MPa20.60.60E21.50E220.6人行道板密度/(kg·m-3)0.241.80×1032.80×1030.24支座竖向刚度/(N·mm-1)+∞104+∞1012

2.5 校验结果合理性评估

本文选取加载挠曲变形最大的主跨1/4位置加载10台车的工况，对现场试验结果、设计模型和校验模型预测的结果进行对比.桥梁钢拱和桥面板的竖向变形见图9，图10.

测点沿桥纵向坐标/m

测点沿桥纵向坐标/m

位置拱肋桥面主跨1/4主跨3/4主跨1/4主跨3/4实测挠度/mm20.00-27.0020.00-51.00设计模型挠度/mm27.00-38.0026.00-55.00校验模型挠度/mm22.00-30.0020.00-53.00校验前η0.740.710.770.92校验后η0.910.901.000.96

表3 前三阶有限元软件计算模态振型与实测结果对比

3 巴溪州大桥结构识别的研究

3.1 桥梁概述

巴溪洲景观桥位于长沙市坪塘，全桥长280 m，主跨部分为180 m.拱肋结构为全焊提篮式钢箱拱，钢拱肋的拱轴线在空间上为悬链线形式，拱轴系数1.8，跨径142 m，矢高24.89 m，拱肋截面内倾角为8°.箱型截面尺寸为1.0 m×1.8 m，两片拱肋通过5道钢箱横撑连为整体.拱肋沿纵向分3种节段类型：钢筋混凝土结合段、钢拱肋A段和钢拱肋B段.吊索直接承受来自桥面主梁的荷载，间距为6.25 m，沿桥梁纵向布设，全桥共设23对，桥梁照片见图11.

图11 巴溪洲桥照片

3.2 静载试验

静载试验记录了巴溪洲桥在载重卡车荷载作用下各个控制截面的应力、应变等数据，全面反映了结构的工作状况.试验共设置14个工况，分为桥梁纵向1/2位置和1/4位置加载.加载车辆平均重量为270 kN，加载稳定后通过全站仪读取桥面和钢拱的变形.在后续的校验模型评估阶段，本文选取了桥面挠曲变形最大的1/2位置加载4台车工况，如图12所示.

图12 静载试验加载布置图

3.3 模态试验

为准确模拟桥梁实际工作状况，巴溪洲桥模态测试通过环境振动(风、水波冲击、行人荷载和地脉动等)激励结构的响应.工作模态分析结果通过随机子空间识别法提取，测点布设如图13所示.

图13 模态测试测点布置图

其中，第11#点和44#点被设为参考点，其余为移动测点，数据采集工作由LMS Cadax-8系统完成.测试过程先后测取桥梁的竖向模态以及横向弯曲模态，每次采集时间为15 min，采样频率为256 Hz.竖向模态的测试中，经过信号处理和频谱分析所得到的模态提取图如图14所示.

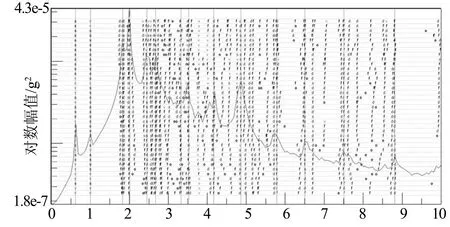
频率/Hz

3.4 有限元建模及分析

巴溪洲桥的设计模型通过有限元软件Midas建立(如图15所示)，所有构件都使用空间梁单元模拟，设计模型采用的建模方法基本满足施工控制和结构工作状况评估的要求.

校验模型的建立综合采用了梁单元、桁架单元、实体单元等.桥面系通过梁格法[25]建立，利用等效的梁格代替桥梁上部结构，将分散在梁、板每一区段内的弯曲刚度和扭转刚度集中于最邻近的等效梁格内，每一梁格内的弯矩、剪力和扭矩均等于该梁格所代表的实际结构的内力.校验模型中，拱肋两端的大体积混凝土由实体单元模拟；吊索采用仅承受拉力的桁架单元模拟；刚性吊杆采用梁单元模拟，并且释放梁端的约束.桥头支座被模拟为简单支撑，支座节点沿x轴、z轴的转动位移和沿x,y和z3个方向平动位移均被限制，模型示意见图16.

图15 巴溪洲桥设计模型

图16 巴溪洲桥校验模型

对于校验模型，根据环境振动测试的工作模态分析和有限元模型理论模态分析的频率相对误差建立目标函数.根据工程经验选取部分不确定性较高的灵敏度参数及其相应的变化范围.C40混凝土容重的灵敏度分析曲线如图17所示.其中，横轴表示混凝土容重相对于初始设计值的变化过程，E为初始设计值，竖轴为前3阶模态频率的相对误差之和.参数校验基于最小二乘法原理，所选取的3个待修正的不确定性参数可见于表4.目标函数选取如公式(2)所示.其中，n=3，即模型校验的目标是实现有限元模态分析前3阶模态频率与工作模态分析结果的契合.修正过程的自变量个数为3，每次修正均固定其余两个自变量，在当前修正自变量的界限内寻找满足目标函数极小值的最优点，并将其确定为校验结果.

3.5 校验结果合理性评估

为了评估模型校验结果的合理性，本文选取加载变形最大的主跨1/2位置加载4台车工况下结构的变形进行研究.钢拱测点布置在其四等分点上，桥面板的边跨测点布设在其跨中，主跨测点布置在所有的八等分点上，挠曲变形数据结果见图18，图19.对比试验和两种有限元模型的计算结果，钢拱和桥面测点的变形与模型预测结果一致，且大部分测点位移小于相应的有限元解析解.

混凝土容重

参数参数设计值变量下界变量上界校验结果钢拱弹性模量/MPa2.06×1050.88E01.04E01.87×105C40混凝土容重/(kN·m-3)25.0022.5030.0026.30桥面铺装重量/(kN·m-1)37.6030.0056.4040.30

为了更加清晰地反映巴溪洲大桥在加载时的工作状况，部分关键位置的校验系数见表5.对比两种模型的校验系数，设计模型能够完成结构在外部荷载作用下承载变形性能的初步预测，而经过精确的现场勘验和单元模拟，以及由模态参数目标函数完成参数校验的校验模型对结构工作状况的评估和响应预测更为准确可靠，其控制测点的校验系数均高于设计模型的相应结果.

测点沿桥纵向坐标/m

测点沿桥纵向坐标/m

巴溪洲桥的工作模态分析和计算模态分析结果

见表6.相比于设计模型，校验模型的静载变形结果和模态分析结果均更加符合巴溪洲桥的现场试验数据，真实全面地模拟了实际结构，验证了有限元模型校验的合理性.

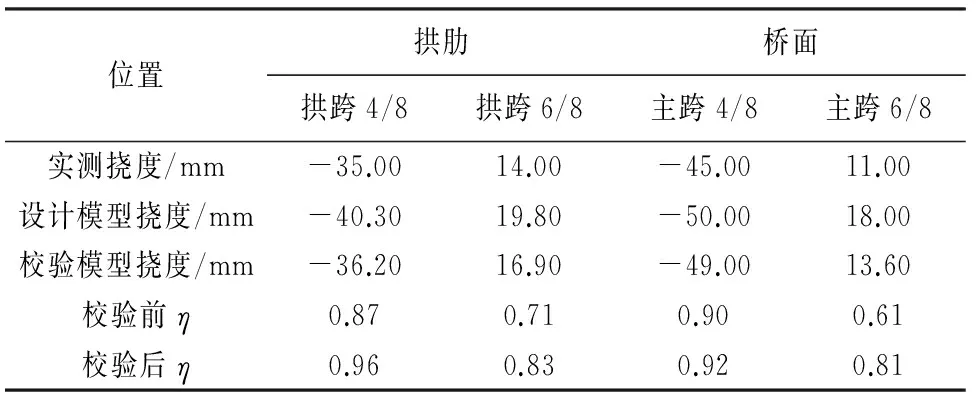
表5 挠度校验系数对比

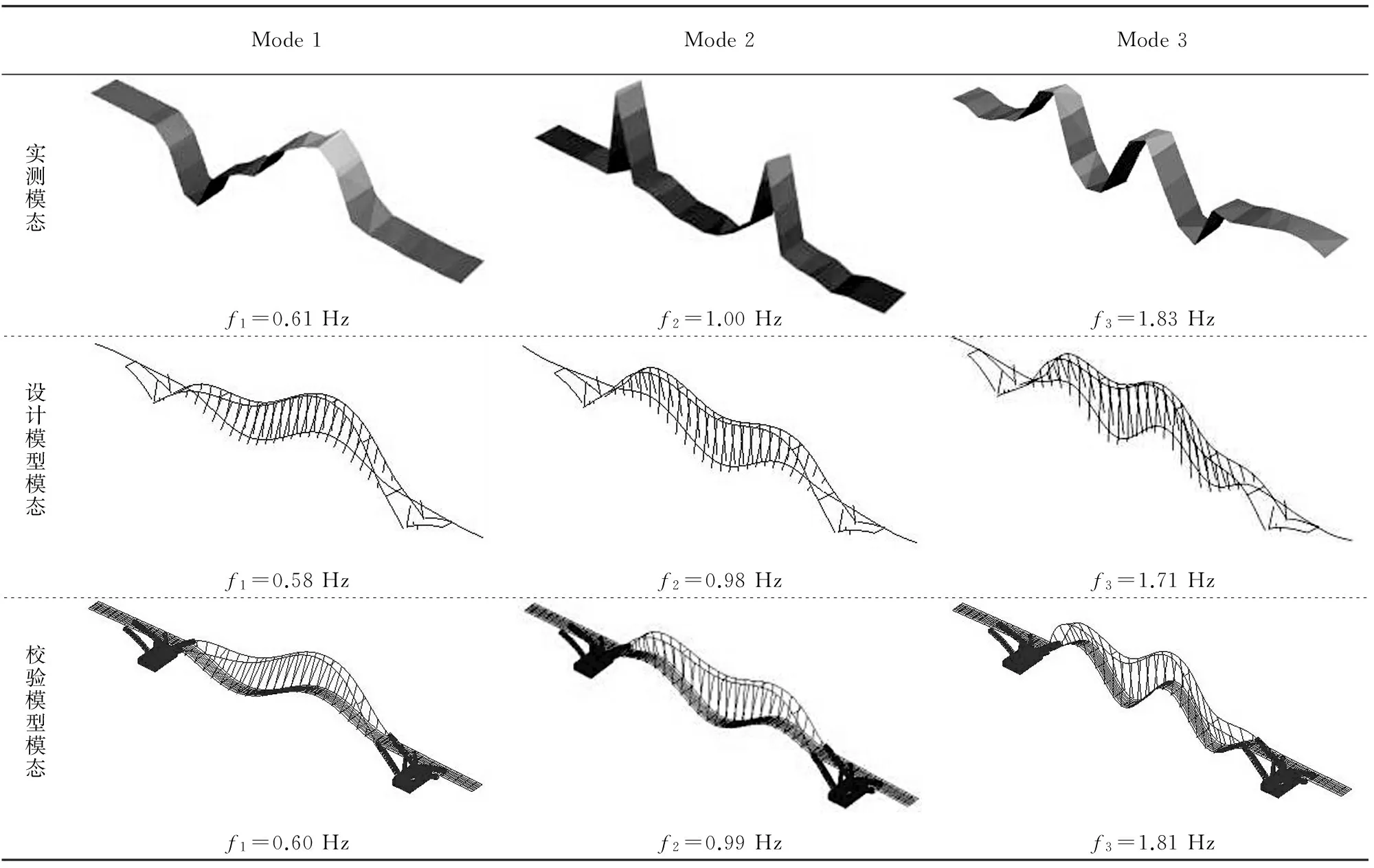
表6 前三阶有限元软件计算模态振型与实测结果对比

4 结 论

大跨度拱桥是以推力为主的结构，其施工质量控制难度大，且构件的性能变化难以观测.构件的物理参数存在一定的不确定性，传统方法难以实现准确的状态评估.本文以团队测试过的两座大跨度拱桥为研究对象，按照初始设计模型、现场试验、模型校验、校验结果评估等步骤完成了两座大跨度拱桥的结构识别.

1)大跨度拱桥结构中构件与材料性质复杂，使用有限元方法对其模拟的过程引入了大量的物理参数和几何参数不确定性.通过对比两座大桥的初始设计模型和其工作模态分析的结果，使用仅基于设计图纸建立的设计模型进行两座桥梁校验系数的评估分别存在着21%和23%的误差，设计模型仅能作为实际结构的先验与近似.

2)综合考虑大跨度拱桥模态频率匹配的目标函数配合最小二乘优化算法可以有效地减小有限元模型与真实结构的参数误差.其中，灵敏度分析可以迅速筛选重要的不确定性参数.完成参数的迭代优化计算后，来华大桥与巴溪洲桥有限元模型的计算模态分析误差分别缩小了16.24%和3.25%.

3)基于现场勘测的真实结构细节模拟和基于模态参数目标函数的重要不确定性参数校验过程，大幅降低了初始有限元模型中的几何参数与物理参数不确定性.校验模型的变形数据和现场静载试验结果更为一致，为进行准确可靠的大跨度拱桥工作状况评估和响应预测奠定了基础.

[1] 钟善桐. 钢管混凝土结构[M]. 北京：清华大学出版社, 2003:73-83.

ZHONG Shantong. The concrete-filled steel tubular bridge structures [M]. Beijing: Tsinghua University Press, 2003:73-83. (In Chinese)

[2] 张跃红. 钢管混凝土拱桥的损伤识别研究[D].大连:大连理工大学土木工程学院, 2006:1-3.

ZHANG Yuehong. Study on damage detection of the concrete-filled steel tube arch bridge [D]. Dalian: College of Civil Engineering Dalian University of Technology, 2006:1-3. (In Chinese)

[3] NAZMY A S. Stability and load-carrying capacity of three-dimensional long-span steel arch bridges [J]. Journal of Computers and Structures, 1997,65(6):857-868.

[4] REN W X, ZHAO T, HARIK I. Experimental and analytical modal analysis of steel arch bridge [J]. Journal of Structural Engineering, 2004, 130(7):1022-1031.

[5] GIOVANNA Z, HONG H, YONG X,etal. Stiffness assessment through modal analysis of an RC slab bridge before and after strengthening [J]. Journal of Bridge Engineering, 2006, 11(5):590-601.

[6] FILIPE M, CUNHA A, CAETANO E. Dynamic monitoring of a long span arch bridge [J]. Engineering Structures, 2008, 30(11):3034-3044.

[7] SONG Y, LEI Y. Application of wireless sensing system for the wuyuan steel arch bridge [C]// Earth and Space． Long Beach， California．United States:ISBN,2008:1-6.

[8] WEI L, HE Q. Health state evaluation for multi-span double-curvature arch bridge based on static-dynamic load testing [C]// ZHANG Jiajie,China． Curran Associates Inc,2011:17-24.

[9] QIN P, GRIMMELSMAN K, MOON F,etal, Mitigating epistemic uncertainty in structural identification：case study for a long-span steel arch bridge [J].Journal of Structural Engineering,2011,137(1):1-13.

[10]李晰,张德义,闫维明,等. 基于环境激励的钢管混凝土拱桥工作模态识别及修正[J].工程力学,2013,30(9):81-94.

LI Xi, ZHANG Deyi, YAN Weiming,etal. Operational model identification and calibration of CFST arch bridge based on ambient excitation [J]. Engineering Mechanics,2013,30(9):81-94. (In Chinese)

[11]胡志坚, 张明辉, 孔祥韶, 等. 大跨度钢桁架拱桥静动力相似模型[J]. 中国公路学报,2014,27(9):82-89.

HU Zhijian, ZHANG Minghui, KONG Xiangshao,etal. Static and dynamic experimental model for long-span steel-truss arch bridges[J]. China Journal of Highway and Transport, 2014, 27(9):82-89. (In Chinese)

[12]COSTA B, MAGALHAES F, CUNHA A,etal. Modal analysis for the rehabilitation assessment of the Luiz I bridge [J]. Journal of Bridge Engineering，2014,19(12)：554-564.

[13]陈清军，周成杰，杨永胜. 基于环境振动信号的框架结构震后损伤识别[J]. 湖南大学学报:自然科学版,2014,41(9):20-26.

CHEN Qingjun, ZHOU Chengjie, YANG Yongsheng. Damage identification of frame structure after earthquakes based on environmental vibration records [J]. Journal of Hunan University: Natural Sciences，2014,41(9):20-26. (In Chinese)

[14]周云,蒋运忠,易伟建,等. 基于模态柔度理论的结构损伤诊断试验研究[J]. 湖南大学学报:自然科学版,2015,42(5):36-45.

ZHOU Yun, JIANG Yunzhong, YI Weijian,etal. Experimental research on structural damage detection based on modal flexibility theory [J]. Journal of Hunan University: Natural Sciences， 2015,42(5):36-45. (In Chinese)

[15]FRISWELL M I, MOTTERSHEAD J E. Finite element model updating in structural dynamics [M]. Netherlands: Kluwer Academic Publishers,1995:98-125.

[16]MOTTERSHEAD J E, FRISWELL M I. Model updating in structural dynamics: a survey [J].Journal of Sound and Vibration, 1993,167(2):347-375.

[17]HART G C, YAO J T P. System identification in structural dynamics [J]. Journal of the Engineering Mechanics Division,1977,103(6):1089-1104.

[18]LIU S C, YAO J T P.Structural identification concept [J].Journal of Structural Division,1978,104(10):1845-1858.

[19]CATBAS F N, KIJEWSKI-CORREA T, AKTAN A E. Americal society of civil engineers． structural identification (St-Id) of constructed facilities: Approaches, methods and technologies for effective practice of St-Id [R]. United States,2011:102-106.

[20]SMITH I, SAITTA S. Improving knowledge of structural system behavior through multiple models [J]. Journal of Structural Engineering,2008,134(4):553-561.

[21]JAISHI B, WEIXIN R. Structural finite element model updating using ambient vibration test results [J]. Journal of Structural Engineering, 2005,131(4):617-628.

[22]谌润水, 胡钊芳. 公路桥梁荷载试验与结构评定 [M]. 北京:人民交通出版社, 2003:8-12.

CHEN Runshui, HU Zhaofang. Load test and structure evaluation of highway bridge[M]. Beijing: China Communication Press, 2003:8-12. (In Chinese)

[23]董小军. 基于灵敏度分析的结构动力模型修正及损伤识别研究[D].兰州:兰州理工大学土木工程学院,2009:35-36.

DONG Xiaojun. Study on structural dynamic model updating and damage detecting based on sensitivity analysis [D]. Lanzhou: College of Civil Engineering, Lanzhou University of Technology,2009:35-36. (In Chinese)

[24]AKTAN E, ÇATBA N, TÜRER A,etal. Structural identification: analytical aspects [J]. Journal of Structural Engineering, 1998,124(7):817-829.

[25][英]汉勃利 Y E C. 桥梁上部构造性能[M]. 郭文辉,译.北京:人民交通出版社,1982:56-68.

HAMBLY E C. Bridge deck behavior[M]. GUO Wenhui, Translated. Beijing: China Communication Press, 1982: 56-68. (In Chinese)

Practice of Static and Dynamic Experiments and Structural Identification of Long-span Arch Bridges

ZHOU Yun1,2†, ZHANG Junkai1, CHEN Songbai1, YI Weijian1,2

(1. College of Civil Engineering, Hunan University, Changsha 410082, China;2. Hunan Provincial Key Laboratory on Damage Diagnosis for Engineering Structures, Hunan University, Changsha 410082, China)

Various uncertainties of the FE modeling may have significant impact on structural identification and result in obvious discrepancy between FE model analysis and field test results. In order to eliminate epistemic uncertainty and aleatory uncertainty during model calibration procedure, which contributes to achieve reliable condition assessment and response prediction, two long-span bridges were taken for examples, and several critical issues were discussed. By means of field inspection and blueprint review, simultaneously combined with the precise modeling, uncertain parameter selection was carried out based on sensitivity analysis, and parameter optimization was eventually performed by the least square method to complete the working condition assessment and response prediction. Research in this paper consists of in-situ experiments, precise finite element modeling, model calibration, and model admissibility check. Discrepancies between FE model and field test results can be mitigated by efficient model calibration method, and initial design model generally shows 20% and 23% relative difference.

model checking; long-span bridge; static and dynamic test; operational modal analysis; structural identification

1674-2974(2017)05-0010-10

10．16339/j．cnki．hdxbzkb．2017．05．002

2016-03-07 基金项目：国家重点研发计划专项资助项目(2016YFC0701400，2016YFE0127900)，National Key Research and Development Program of China(2016YFC0701400，2016YFE0127900)；国家自然科学基金青年基金资助项目(51208190)，National Natural Science Foundation of China(51208190) 作者简介：周云(1979-)，男，湖南长沙人，湖南大学副教授，博士 †通讯联系人，E-mail:zhouyun05@126.com

周云1,2†，张军凯1，陈松柏1，易伟建1,2

(1.湖南大学 土木工程学院, 湖南 长沙 410082; 2. 工程结构损伤诊断湖南省重点实验室 湖南大学，湖南 长沙 410082)

U446.1

A