针对大功率脉动负荷的混合储能系统容量优化配置方法研究
王慧娟,张建成
(华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)
针对大功率脉动负荷的混合储能系统容量优化配置方法研究
王慧娟,张建成
(华北电力大学 新能源电力系统国家重点实验室,河北 保定 071003)
大功率脉动负载日益增多,为满足短时冲击负载的用电质量要求,电源需要按最大功率配置,而在低负荷情况下则会造成电源资源浪费,特别是对于一些特殊供电电源还会造成环境污染。储能系统的参与可以缓解这一问题,其容量的合理配置则是治理效果和经济性的决定因素。提出一种针对大功率脉动负荷情况的蓄电池-超级电容器混合储能系统容量优化配置方法,该方法采用经验模态分解方法求出分界频率来确定蓄电池和超级电容器之间的功率分配;以全生命周期成本最低为目标函数,考虑能量损失率和负荷缺电率等约束条件,利用遗传算法进行求解。编制了混合储能系统容量优化配置计算软件,最后利用编制的软件对某钻井机工作系统进行混合储能系统容量优化配置计算,结果验证了所提方法的有效性。
混合储能;脉动负荷;分界频率;能量损失率;负荷缺电率
0 引 言
目前,功率具有脉动性的负载日益增多,如移动数字设备、电动汽车和定向能武器等,其典型特征是峰值功率很高,但平均功率较低[1-2]。当驱动脉动负荷时,需要具有较高功率输出能力的电源。石油钻井机作为大功率脉动负载,绞车下钻时处于轻负荷状态,而起钻时其功率出现短时的冲击峰值,这就使得功率分布不均匀。利用储能装置将下钻时多余能量存储起来,来补充起钻时的冲击负荷,这样不但能实现能源的回收利用,同时可降低柴油机的功率配置,达到 “降本增效,节能减排”的目的。
蓄电池技术成熟、性能可靠,被广泛使用,但蓄电池存在一些缺点,如功率密度小、寿命短等[3]。超级电容器具有功率密度大、容量小、循环寿命长的特点[3],与蓄电池相结合组成混合储能系统,可以实现蓄电池和超级电容器的优势互补运行方式,在避免电能浪费的同时,提高了储能系统的整体性能、延长了储能系统运行年限,降低了经济成本。
蓄电池-超级电容器混合储能系统亟需解决的问题之一是,蓄电池和超级电容器两者之间的功率如何分配。目前相关研究大致有以下几方面:利用低通滤波的方法平滑功率的波动[4-5],但是滤波器的时间常数会影响滤波效果和储能系统的优化配置;建立多目标函数,利用粒子群算法对目标函数求最优,同时采用变时间常数功率分配等方法[6-8],此方法中蓄电池和超级电容器的充放电次数会随波动强弱而变化,对储能设备寿命不利;采用离散傅里叶变换确定分界频率,从而进行功率分配[9],此方法是从技术层面进行考虑,没有考虑昂贵的成本问题;利用小波分解来确定超级电容器和蓄电池各自的充放电范围[10-11],此方法中小波分解需要基波作为参考,所以基波的选择会影响配置结果;利用滑动平均法来处理功率[12];通过控制装置的设计来使得容量得到优化[13-14],此方法更多地考虑功率平抑效果,忽略配置经济性;采用经验模态分解的方法来确定功率的分配[15],克服小波分解的缺点,对蓄电池和超级电容器的工作状态进行了优化。
本文将混合储能的应用扩展到含有大功率脉动负荷的传统供电系统,不仅限于光伏、风电等新能源系统。在上述混合储能容量优化方法的研究基础上,本文首先将经验模态和希尔伯特频谱相结合确定出分界频率,根据分界频率确定蓄电池和超级电容器的功率分配;建立全生命周期成本最低的目标函数,考虑能量损失率和能量缺失率等条件的约束,通过遗传算法进行求解。
1 脉动负荷系统一般工作特性
很多工业大功率脉动负荷一般具有周期性大幅度波动特性,为了满足负荷最大功率需求,电源长期存在“大马拉小车或空车”的恶劣现象,严重影响供电电源的运行经济性,甚至带来较大的环境污染问题。图1为某行业大功率脉动负荷一个周期的功率变化情况。

图1 某海上钻井机一个周期内的功率变化情况Fig.1 Power change in a cycle of an offshore drill rig
在图1中,0~160 s为下钻时的功率变化情况,161~411 s为起钻时的功率变化情况。海上钻井平台采用柴油发电机供电,在下钻和起钻过程中,周期性的载荷急剧变化对供电电源平稳运行极为不利,按照最大负荷配置的柴油发电机在功率波动过程中排烟污染增大、运行经济性大幅降低。为了改善柴油发电机的运行状况,可以考虑适量配置储能系统,特别是由蓄电池和超级电容器构成的混合储能系统。通过混合储能系统的充放电运行控制,平衡负荷波动状况、降低柴油发电机的出力波动性和环境污染状况,提高柴油发电机的运行稳定性。
2 蓄电池-超级电容器混合储能系统一般构成及工作原理
图2为蓄电池—超级电容器混合储能系统一般构成图,(a)为混合储能系统直流应用一般构成图,(b)为混合储能系统交流应用一般构成图。大功率脉动负荷有短时的峰值,功率分布不均,利用储能装置在轻负荷时将能量存储起来,在冲击负荷到来时释放能量。混合储能装置中超级电容器负责不平衡功率Pub(发电机和负荷的差值)中频繁波动(高频)部分,蓄电池负责波动平缓(低频)部分。此配置原则上避免了蓄电池频繁充放电,延长了蓄电池的寿命,超级电容器的参与使得充放电速度加快,提高了储能装置的综合性能,使得电能保持平稳。同时减轻了发电机的压力,优化了供电电源的工作状态。
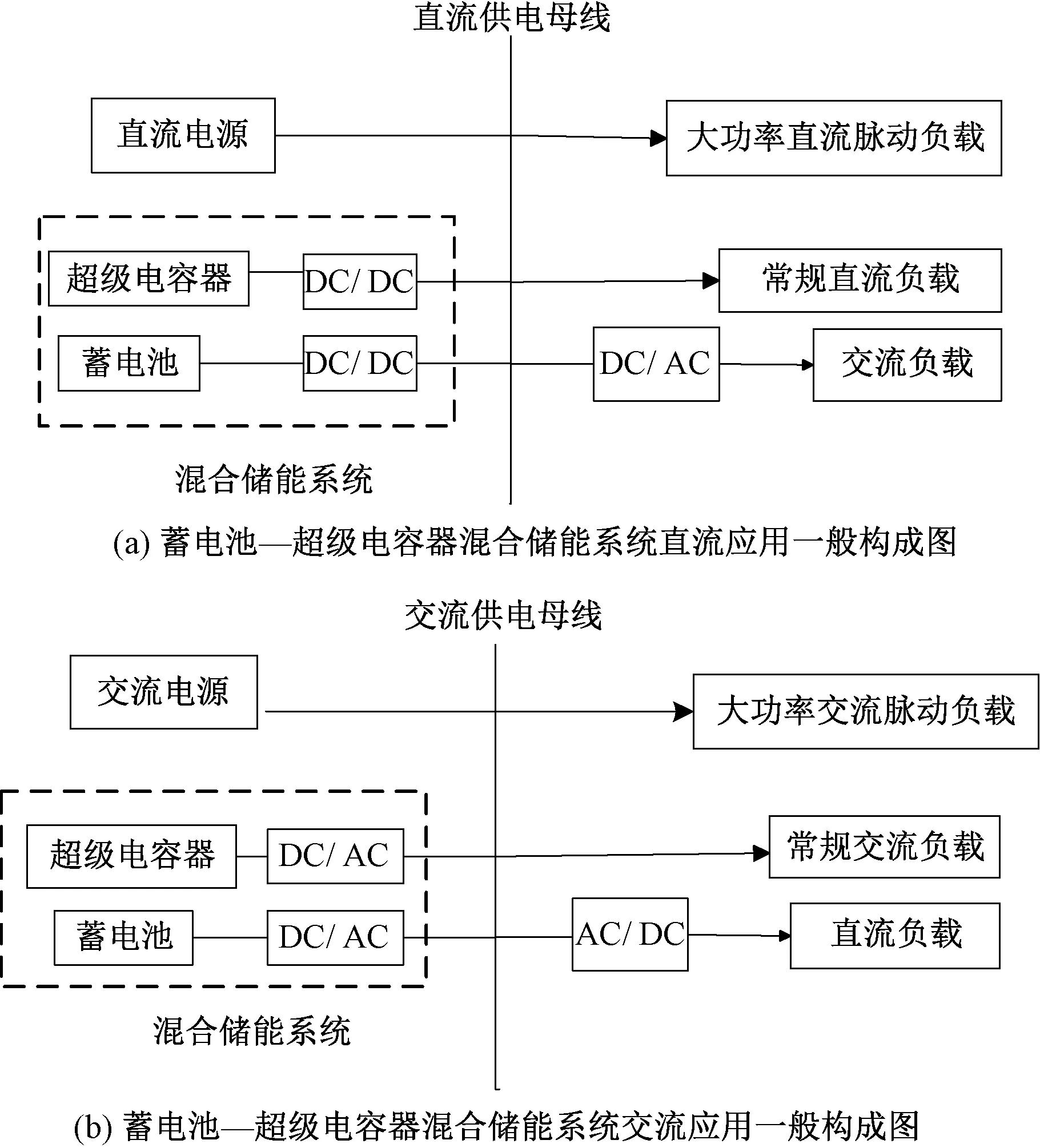
图2 混合储能系统一般构成图Fig.2 Structure of hybrid energy storage system
3 混合储能容量优化
3.1 分界频率的确定
经验模态分解(EMD)和希尔伯特频谱分析相结合对非平稳非线性信号分析能达到不错的效果。EMD不同于傅里叶分解法和小波分解法,EMD根据自身的时间尺度进行信号分解,无需预先设定任何基函数。
经过EMD分解,不平衡功率被分解为一系列固有模态函数ci,并且ci的频率随i的增加是逐渐降低的,利用希尔伯特频谱得到瞬时频率—时间曲线,从这些曲线中寻找分界频率fg,将Pub分为高频和低频两部分。频率高于fg的高频功率分量记为PH,频率低于fg的低频分量记为PL。所以计算公式为
(1)
(2)
选择分界频率的原则是fg与紧邻的两个模态重叠少[13]。
取出ci和ci+1作为例子,在一个周期内进行分析,如图3所示。
假设的分界频率为fg,fi+1和fi分别为ci+1和ci的频率线,从图3可以看出,按PH和PL的计算原则,ci+1应该属于低频部分,ci属于高频部分,但fg与fi+1和fi都相交。即若以fg分界,则fg以上需要超级电容器来负责平抑,本需要由蓄电池来平抑的ci+1的某一部分功率超过了fg,所以超出的这部分也要由超级电容器负责,给超级电容器的储能密度造成压力;同样,fg以下部分需要蓄电池平抑,但是ci有一部分低于fg,由超级电容器来负责变为蓄电池负责,增加蓄电池充放电次数。
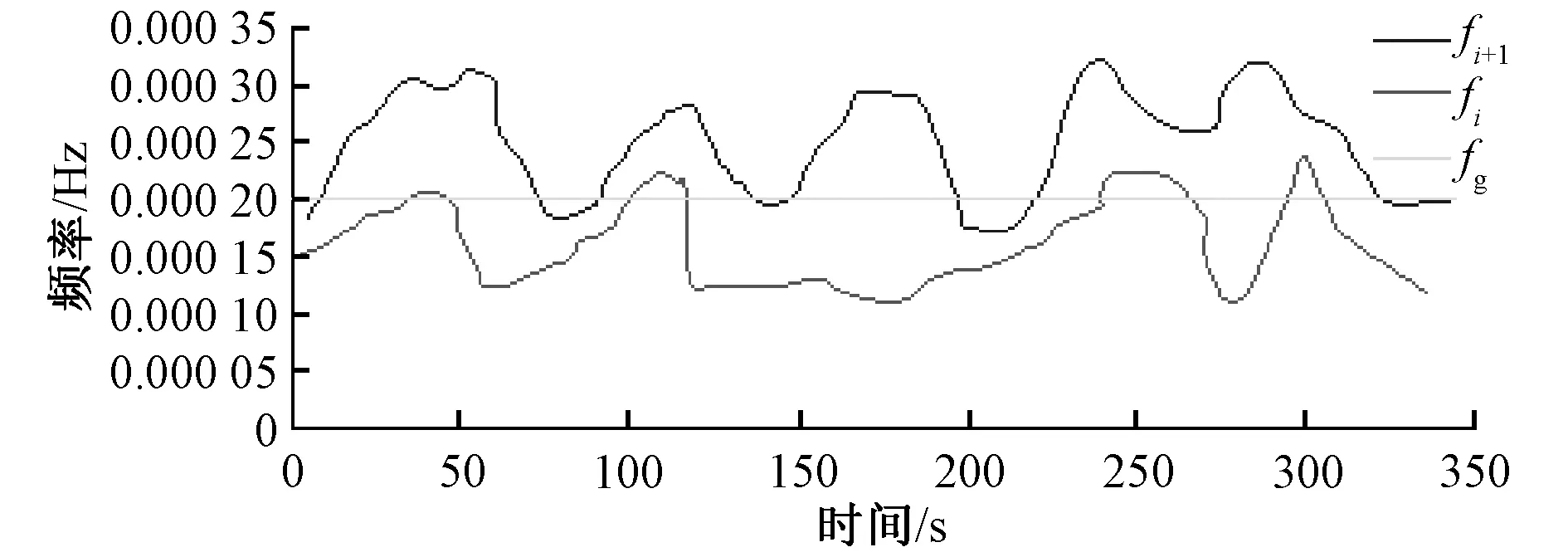
图3 ci和ci+1的频率-时间曲线Fig.3 Frequency-time curves of ci and ci+1
所以要寻求fg低于fi部分和高于fi+1的部分总和最小的分界频率。
3.2 约束条件能量损失率和负荷缺电率计算
本文采用能量损失率(RLPPP)和负荷缺电率(RLPSP)作为运行指标。负荷缺电率为负荷需求EL和供应EG的差ELPSP与需求EL的比值;能量损失率为系统损失的电能ELPPP和发电机发电总量EG的比值[16]。计算如式(3)所示。
(3)
ELPPP的计算流程如图4所示。从图4中可以看出计算ELPPP一共有8种情况,每一种的具体情况分析和计算过程如下:
Q1:不平衡功率Pub经过分解后,高频功率PH大于超级电容器的最大功率Pucmax,低频功率PL大于蓄电池的额定功率Pban,所以超级电容器以最大功率充电Puc=Pucmax,蓄电池以额定功率充电Pba=Pban,并且超级电容器的容量没有达到Eucmax。这种情况计算公式如(4)所示,系统产生的能量损失包括储能系统充电效率产生的损失、因为两者充电功率不足产生的损失。
(4)
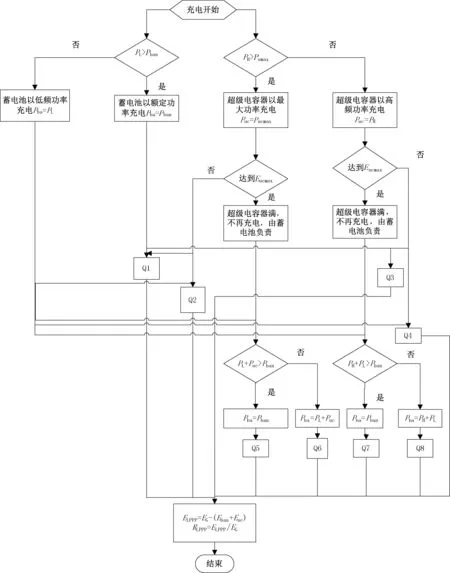
图4 能量损失率的计算Fig.4 Calculation of the loss of produced power probability
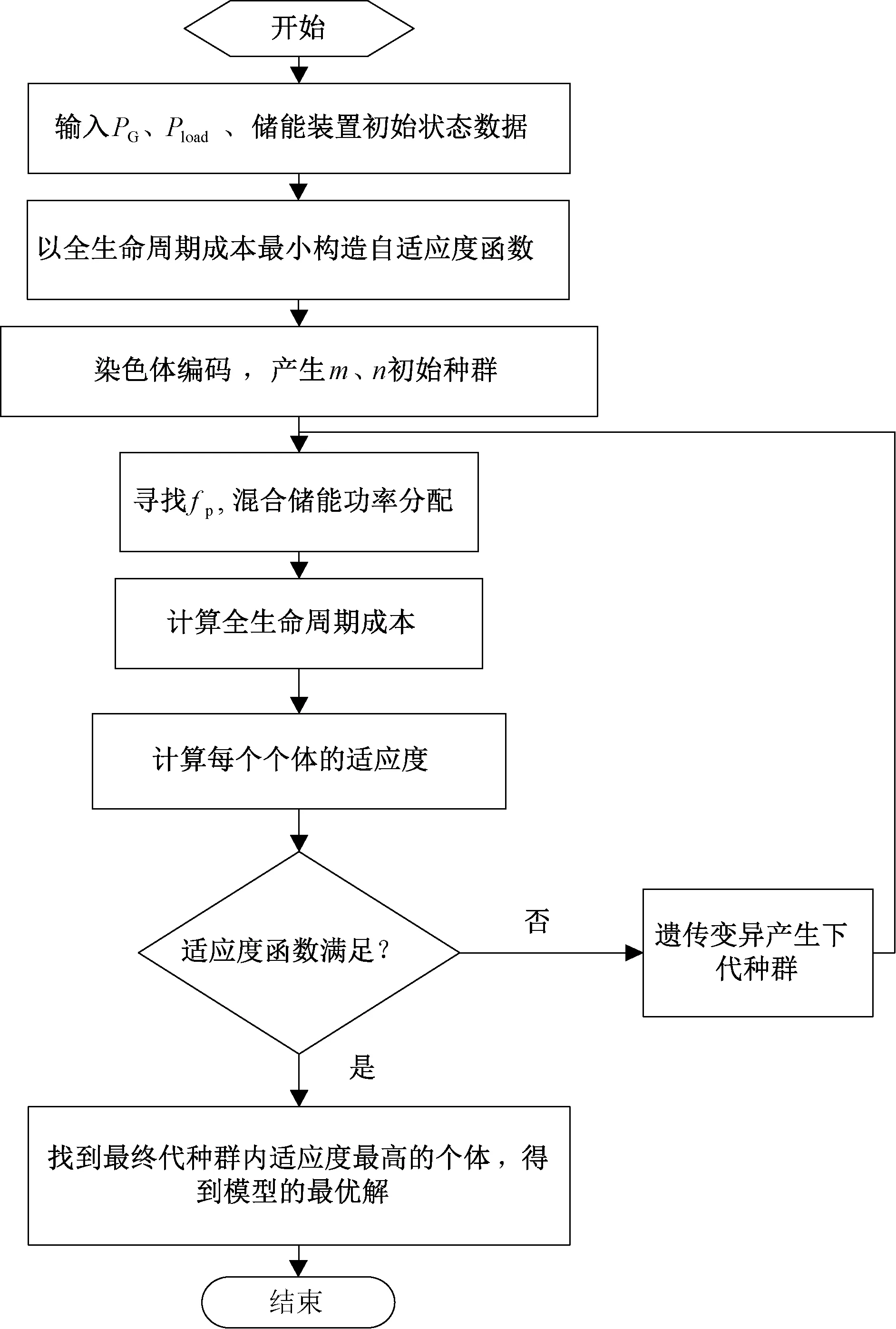
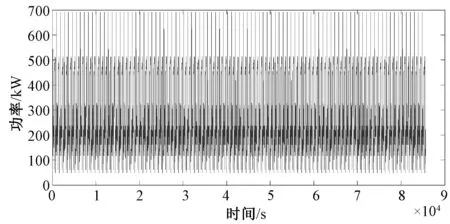
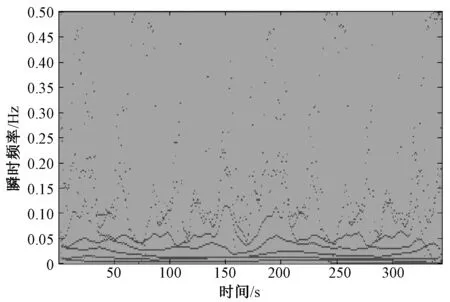
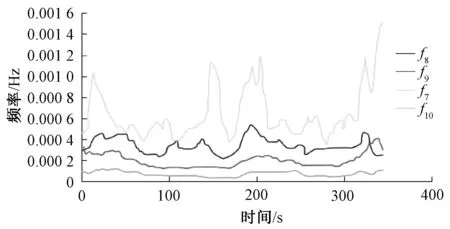
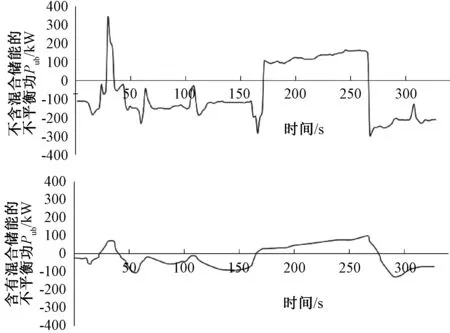
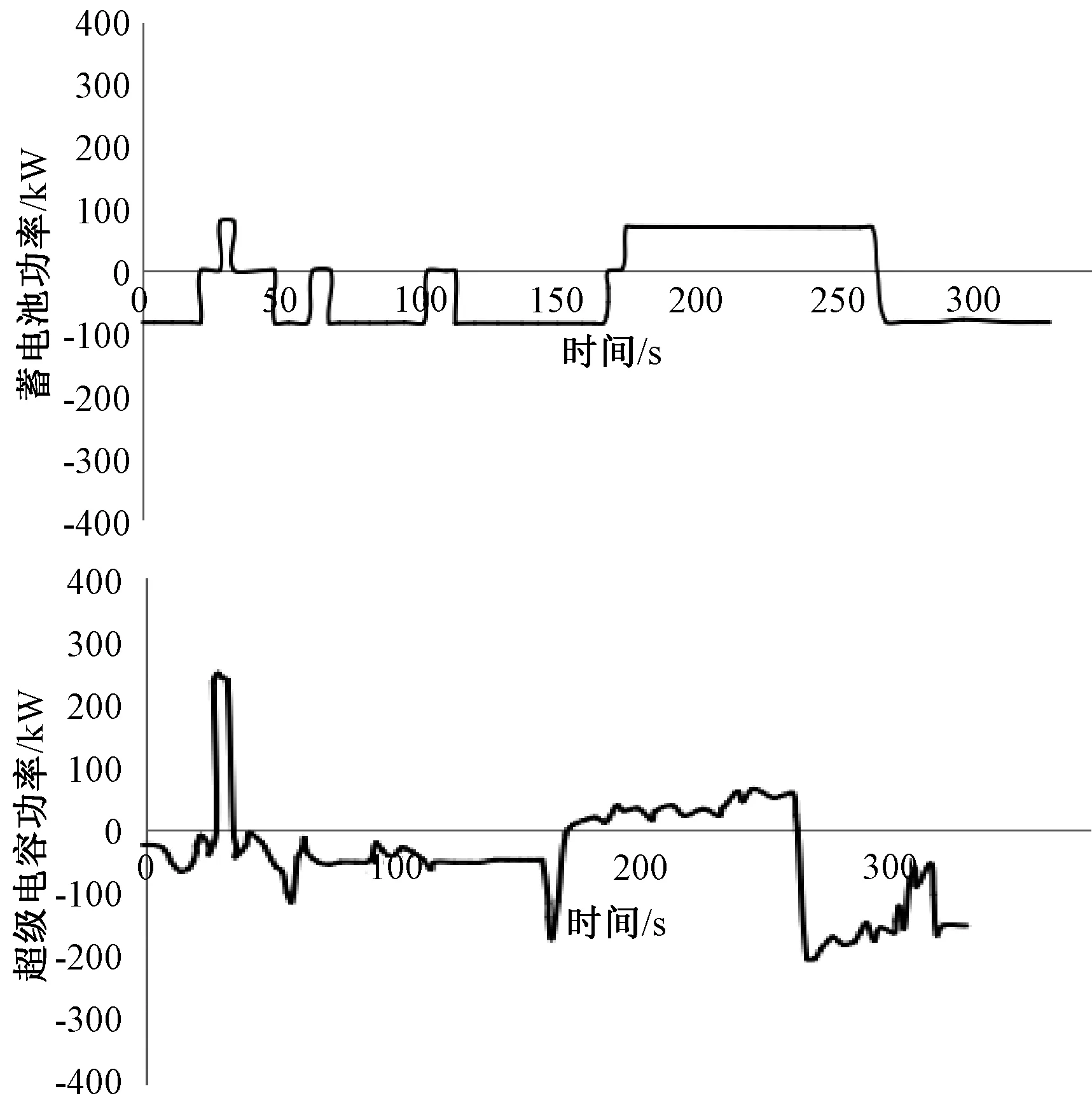
Q2:与第一种情况不同之处在于,PL (5) Q3:与第一种情况不同之处在于,PH (6) Q4:超级电容器的充电功率是Puc=PH,蓄电池的充电功率为Pba=PL。所以能量损失为两种设备由于充电效率产生的部分,如式(7)所示。 (7) Q5:以Q4方式充电到某一时刻t1,超级电容器达到了最大容量Eucmax,在t1时刻后由蓄电池代替超级电容器继续充电,并且PH+PL>Pban,所以Pba=Pban,能量损失包括充电效率和两者充电功率不足产生的两部分,如式(8)所示。 (8) Q6:不同于Q5,t1时刻之后,PH+PL (9) Q7:在t1时刻前,Puc=PH,Pba=PL,t1时刻后超级电容器达到Eucmax,且PH+PL>Pban,此时,Pba=Pban。能量损失为充电效率产生和t1时刻后蓄电池充电功率不足产生,计算如(10)式所示。 (10) Q8:与Q7不同之处是t1时刻后PH+PL (11) 同能量损失率,负荷缺电率ELPSP的计算如图5所示。8种情况下ELPSP计算公式如式(12)~(19)所示。 (12) (13) (14) (15) (16) (17) (18) (19) 式中:κba,κuc为蓄电池和超级电容器的放电效率。 图5 负荷缺电率的计算Fig.5 Calculation of the loss of power supply probability 3.3 容量优化模型 本文以全周期成本最小为目标函数,综合考虑功率平衡、能量损失率、负荷缺电率、储能系统的效率、储能装置特性等,建立蓄电池-超级电容器的混合储能容量优化模型如下: 目标函数: (20) 约束条件如式(21): (21) 式中:Cm为购买设备的费用;Cy为系统运行成本;Cw为维护系统的费用;Cc为装置处置成本。 其中装置的购置成本为 (22) 式中:pba、puc分别为蓄电池组和超级电容器组的单价;m、n分别为蓄电池组和超级电容器组的个数;kdeba、kdeuc分别为蓄电池组和超级电容器组的年折旧值;运行成本为 (23) 式中:koba、kouc分别为蓄电池和超级电容器的运行成本系数;维护成本为 (24) 式中:kmba为蓄电池维护成本系数,超级电容器不用维护;处置成本为 (25) 式中:kdba、kduc分别为蓄电池和超级电容器处置成本系数。 3.4 模型求解 本文采用遗传算法对模型的求解。计算流程如图6所示。 根据输入的发电机发电功率PG和负荷用电功率Pload,构造自适应度函数,经过染色体编码,产生蓄电池和超级电容器组数的初始种群,对不平衡功率进行经验模态分解,寻找分界频率fg,根据fg分配功率,计算全生命周期成本,计算每个m、n的自适应度,这是第一代计算。通过遗传变异产生多代,直到满足自适应度函数为止,最后一代的m、n便是模型的最优解。 图6 模型计算流程Fig.6 Flow chart of mode 以某海上5 000 m石油钻井机工况进行分析计算,发电机组发出的平均功率为350 kW,负荷波动情况为100~800 kW。配置储能装置的参数如下图所示(本文分别以100个和50个串并联构成蓄电池组和超级电容器组)。储能设备参数如表1所示。 负荷功率在24 h内具体变化情况如下图7所示。 不平衡功率经过EMD分解,得到11个固有模态函数,选取一段时间的分解后结果如图8所示。 在这里仅分析c7-c10的频率-时间曲线,如图9所示。从图中可以看出f9和f10几乎没有重叠,所以选择分界频率为fg=0.000 2 Hz,确定分界频率后就可以对混合储能系统进行功率分配,本文采样周期为Ts=344 s (钻井机下钻和起钻一个周期),即蓄电池补偿0~0.000 2 Hz的低频分量,由超级电容器补偿0.000 2~0.001 4 Hz。从分配结果来看,充分利用了超级电容器功率大的优势。 表1 储能系统装置参数 图7 一日内功率变化Fig.7 Power in a day 图8 不平衡功率分解后的瞬时频率—时间曲线Fig.8 Frequency-time curves of resolve imbalanced power 图9 c7-c10的频率-时间曲线Fig.9 Frequency-time curves of c7-c10 根据得到的分界频率,将储能设备参数等带入编制的软件中对蓄电池和超级电容器最优组数进行计算。软件中遗传算法的相关参数如下:交叉概率为0.1,变异概率0.01,最大代数为50,种群大小为200。求得蓄电池的组数为8,超级电容器的组数为2,蓄电池和超级电容器的折旧率分别为0.244 3和0.038 4,在这种情况下,求得全寿命周期成本为32万元。 系统的不平衡功率如图10所示: 图10 不含有混合储能及含有混合储能的不平衡功率Fig.10 Pub and smoothed by hybrid energy storage system 由图10可以看出,加入混合储能系统避免了电能的大量浪费。在冲击负荷出现时,储能系统释放电能,因此供电电源不必以负荷最大功率进行配置,降低了成本;轻负荷时,储能系统吸收电能,使得供电电源燃料能够充分燃烧,减轻了环境污染。 图11 蓄电池及超级电容器功率变化Fig.11 Power change of battery and super capacitor 图11为蓄电池和超级电容器在充放电过程中的功率变化情况,由于超级电容器补偿了不平衡功率中的高频分量,蓄电池深度充放电次数减少,延长了寿命,提高混合储能系统的整体性能。 本文根据超级电容器和蓄电池的储能特性寻找分界频率,合理分配功率;研究了系统能量损失率和负荷缺电率的计算方法与流程;建立了以全生命周期费用理论为基础的储能容量配置优化目标函数,并运用遗传算法对函数进行求解。该方法可以有效降低电源冗余容量配置,降低了系统综合运行成本,最后通过算例验证了所提方法的有效性。 [1] 王琪, 孙玉坤, 黄永红. 应用于脉冲电流负载的复合电源设计[J]. 浙江大学学报(工学版), 2015,49(8):1537-1543. [2] 唐西胜. 超级电容器储能应用于分布式发电系统的能量管理及稳定性研究[D]. 北京: 中国科学院, 2006. [3] 张国驹, 唐西胜, 齐智平. 平抑间歇式电源功率波动的混合储能系统设计[J]. 电力系统自动化,2011,35(20):24-28. [4] 李军徽. 抑制风电对电网影响的储能系统优化配置及控制研究[D].保定:华北电力大学,2012. [5] 文艺. 风力发电系统中储能容量优化配置[D]. 武汉:华中科技大学,2013. [6] 钟永. 微电网储能系统容量优化与控制策略研究[D]. 上海:上海电力学院,2014. [7] 吴云亮, 孙元章,许箭. 基于饱和控制理论的储能装置容量配置方法[J].中国电机工程学报, 2011, 31(22): 32-39. [8] 候世英,房勇,孙韬. 混合储能系统在独立光伏发电系统功率平衡中的应用[J]. 电网技术,2011, 35(5): 183-187. [9] 王成山, 肖俊. 平滑可再生能源发电系统输出波动的储能系统容量优化方法[J]. 中国电机工程学报,2012,32(16):1-8. [10] 肖俊,张泽群,张磐. 用于优化微网联络线功率的混合储能容量优化方法[J]. 电力系统自动化,2014,38(12):19-26. [11] 江海生. 应用于平抑风电功率波动的多类型储能系统容量配置与协调控制研究[D]. 浙江:浙江大学,2013. [12] 韩晓娟,陈跃燕,张浩,等. 基于小波包分解的混合储能技术在平抑风电场功率波动中的应用[J]. 中国电机工程学报,2013, 33(19): 8-13. [13] 马苏良,蒋小平,马会萌,等. 平抑风电波动的混合储能系统的容量配置[J]. 电力系统保护与控制,2014, 42(8): 108-114. [14] 戚艳. 微网广义储能系统协调控制策略及容量优化配置方法研究[D]. 天津:天津大学, 2013. [15] 孙承晨,袁越,San Shing CHOI,等. 基于经验模态分解和神经网络的微网混合储能容量优化配置[J]. 电力系统自动化, 2015, 39(8):19-26. [16] 杨珺,张建成,鲍雪娜. 针对独立风光发电中混合储能容量优化配置研究[J]. 电力系统保护与控制,2013, 41(4): 38-44. [17] 田军. 分布式发电系统储优化配置[D]. 保定:华北电力大学,2011. [18] 谢世骁. 混合储能系统控制策略与容量配置研究[D]. 浙江:浙江大学,2012. [19] 胡烈良. 可再生能源接入直流微网的运行控制分析[D]. 广州:华南理工大学,2011. [20] 李嘉琛. 并网光伏电站中混合储能的控制与容量优化策略的研究[D]. 太原:太原理工大学,2011. [21] 朱向芬.基于粒子群算法的混合储能系统容量优化配置[D]. 宁夏:宁夏大学,2014. [22] 谭兴国. 微电网复合储能柔性控制技术与容量优化配置[D]. 济南:山东大学,2014. [23] LI Wei, JOOS G, BELANGER J. Real-time simulation of a wind turbine generator coupled with a battery super capacitor energy storage system [J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): l137-1145. [24] ALLEGRE A L, BOUSCAYROL A, TRIGUI R. Influence of control strategies on battery/super capacitor hybrid Energy Storage Systems for traction applications [A]. Vehicle Power and Propulsion Conference[C]. Dearborn: IEEE, 2009: 2l3-220. [25] ZHANG Yu, JIANG Zhenhua, YU Xunwei. Small-signal modeling and analysis of battery-super capacitor hybrid energy storage systems [C]. Power & Energy Society General Meeting. Calgary: IEEE, 2009: 1-8. Research on Capacity Optimization of Hybrid Energy Storage System with High-power Pulsating Load WANG Huijuan,ZHANG Jiancheng (State Key Laboratory of Alternate Electrical Power System with Renewable Energy Sources,North China Electric Power University,Baoding 071003,China) Maximum power of power supply will meet the demand of electricity quality for short-term impact load as the high-power pulsating load increases day by day. However, under the circumstance of low load, it will cause the waste of power resources or pollute environment for some special power supply. Energy storage system can deal with the problem and the treating effect and economic performance are mainly determined by reasonable capacity allocation of the storage system. The paper presents a capacity optimization method of hybrid energy storage system for high-power pulsating load. Empirical mode decomposition (EMD) is used to calculate the dividing frequency so as to allocate power between the battery and the super capacitor. Lowest life cycle cost is the objective function. Genetic algorithm is used to calculate when taking constraint conditions like the loss of produced power probability (LPPP) and the loss of power supply probability (LPSP) into account. Software for optimal allocation of the capacity of the hybrid energy storage system is programmed. Finally, capacity optimization of hybrid energy storage system for a drilling rig working system is done by the above software and the result verifies the effectiveness of the proposed method. hybrid energy storage system; pulsating load; dividing frequency; loss of produced power probability; loss of power supply probability 10.3969/j.ISSN.1007-2691.2017.03.05 2016-07-21. 国家自然科学基金资助项目(51177047);河北省科技支撑项目(16214504D). TM731 A 1007-2691(2017)03-0030-09 王慧娟(1990-),女,硕士研究生,研究方向为混合储能容量优化;张建成(1965 -),男,教授,博士生导师,研究方向为新型能量储存技术、电能质量控制技术和新能源发电控制技术等。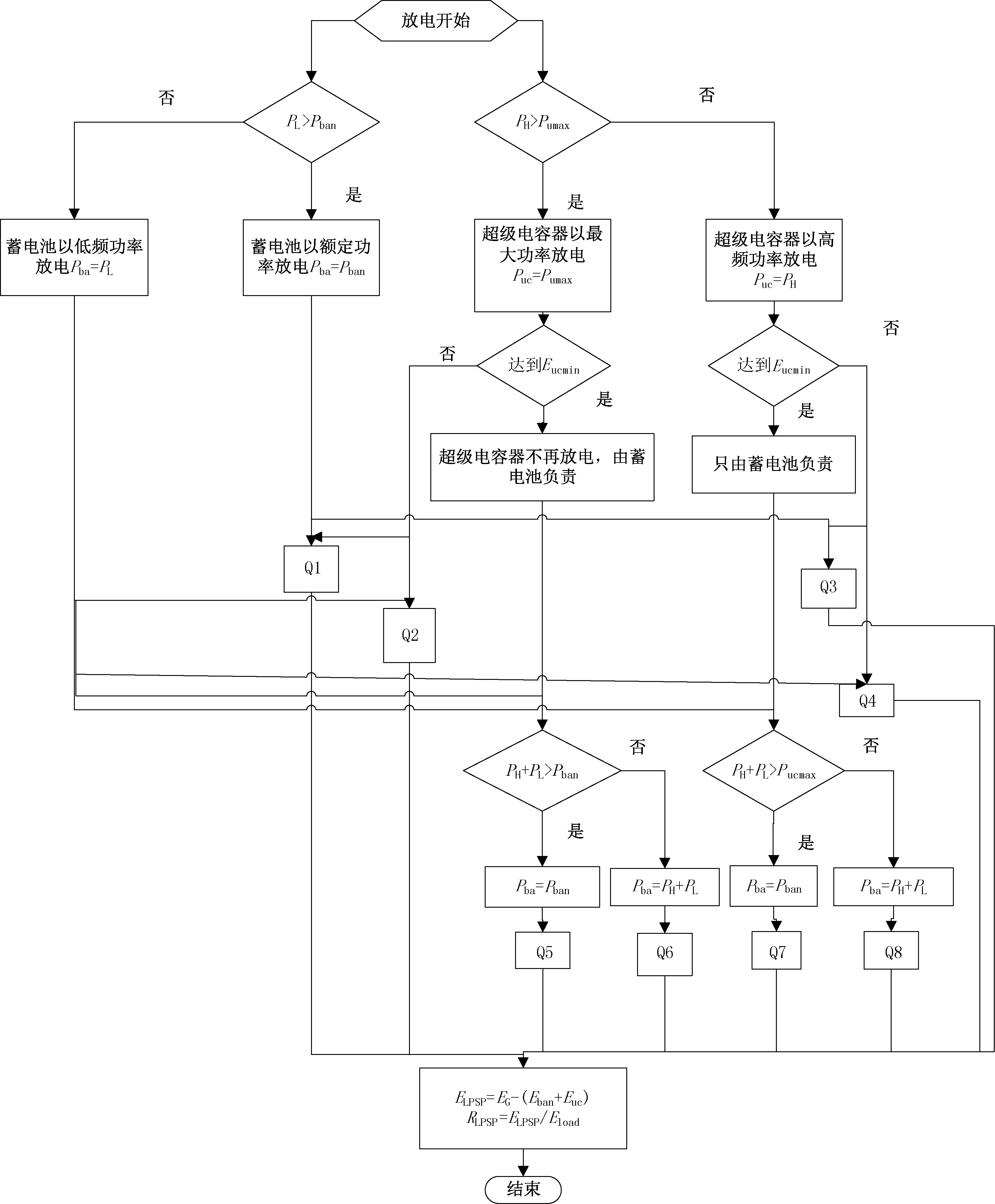
4 实例验证

5 结 论

