分数阶元件伴生模型的建立及其仿真计算研究

梁贵书，单栋清

(华北电力大学 电气与电子工程学院，河北 保定 071003)



分数阶元件伴生模型的建立及其仿真计算研究

梁贵书，单栋清

(华北电力大学 电气与电子工程学院，河北 保定 071003)

通过对比多种分数阶元件实现方法，选取L1插值逼近法建立分数阶元件的伴生模型，并通过仿真计算验证了该分数阶元件伴生模型的可行性及准确性。采用稀疏表格法编写分析分数阶电路的通用程序，实现了任意线性分数阶电路和部分非线性分数阶电路的自动求解，可作为分析分数阶电路的辅助工具，弥补了 现有电路分析软件不能对分数阶电路仿真的不足。

分数阶元件；伴生模型；分数阶电路；稀疏表格法；自动求解

0 引 言

分数阶微积分理论具有全局记忆特性，近些年在诸多领域得到了越来越广泛的应用，如电气工程、力学、信号学、生物学、控制领域、经济学等[1-4]。

整数阶微积分理论只能描述整数阶电容，为了更加准确地描述电容器的一些特有性质，R.Martin等人提出了电容器的分数阶模型[5]。文献[6,7]实现了0.59阶、0.42阶的分数阶电容，而Tenreiro Machado等人基于集肤效应制造出了任意阶次的电感[8]。以上研究表明电容和电感在本质上均为分数阶元件。

PSpice、Multisim等传统的电路分析软件对储能电路的仿真都基于储能元件的离散伴生模型，伴生模型可以将电路微分方程转化为代数方程进行求解[9]。这些传统的电路仿真软件中没有涉及到分数阶元件，不能分析分数阶电路。

目前，简单分数阶电路一般采用频域方法或手动列写电路状态方程的方法进行分析，这些方法不适用于结构复杂的电路。为了分析任意分数阶电路，有必要建立分数阶元件的离散伴生模型，它是分数阶电路仿真分析的基础。本文采用Caputo分数阶导数的L1插值逼近方法[10]建立分数阶元件的离散伴生模型，并通过仿真验证了模型的可行性与精确性。

1 分数阶元件的离散伴生模型

1.1 分数阶元件

分数阶元件包括分数阶电容和分数阶电感，其频域内阻抗表达式为

(1)

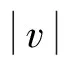
(2)

(3)

式中：α和β分别为分数阶电容、电感的阶次；Cα、Lβ分别为表示分数阶电容、电感，其单位分别为F/s1-α、H/s1-β。

1.2 分数阶导数离散逼近方法比较

分数阶导数的离散逼近方法有：电路实现的算法逼近[12]，R-L分数阶导数的G-L逼近[13]、位移G-L定义逼近[14]，Caputo分数阶导数的Alikhanov超收敛插值逼近[15]，Caputo分数阶导数的L1插值逼近等，本文将Caputo分数阶导数的L1插值逼近简称为L1插值逼近。

采用电路实现的算法逼近具有诸多缺点：电路实现条件严格、电路设计复杂、实现阶次相对固定，经常涉及到网络综合，而网络综合不满足正实条件时会产生负元件，不能保证电路的稳定性，实现误差大等，这些缺点使通用程序的编写相当困难。

G-L逼近或者位移G-L逼近这两种算法的精度具有一阶精度[16]，对于某些问题在某些区域内其离散误差可能会很大，用这两个公式去离散分数阶微分方程可能会产生一个完全不相容的差分格式，因而差分解不一定完全收敛，所以此法也不适用于建立分数阶元件的伴生模型。而Alikhanov超收敛插值逼近利用二次插值进行离散逼近，算法复杂度比L1插值法高，计算量大，计算时间长。L1插值逼近法算法稳定性、收敛性好，可以满足精度要求。通过比较与分析以上几种方法，本文选取L1插值逼近法建立分数阶元件的离散伴生模型。

1.3 分数阶元件的离散伴生模型

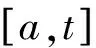
(4)

其中n=[α]+1，Γ(·)为Gamma函数。当0<α<1且a=0时，式(4)变为

(5)

对式(5)进行L1插值离散逼近得

(6)

式中

(7)

式(6)即为Caputo分数阶导数的L1插值逼近公式，该式表明：求解tn时刻的f(t)分数阶导数值，仿真程序中需要存储和调用t0、t1、…、tn所有时刻的值，算法的时间复杂度为Ο(n2)，计算时间与采样点数的平方成正比。文献[17]证明了此方法的稳定性和收敛性，离散逼近的误差为

(8)

式中：c1为常数，可知随着步长Δt的减小，误差也逐渐减小，因此L1插值离散逼近方法是收敛的。式(2)和(6)联立得

(9)

i(tn)=i(t)|t=tn，有

(10)

式中令

(11)

(12)

式(10)可表示为

(13)

式(13)即为分数阶电容的离散伴生数学模型，据此建立图1所示分数阶电容的离散伴生模型。分数阶电容在tn时刻可以等效为一个值为Geq的电导和一个值为i(tn-1)的电流源并联，等效电流源的电流i(tn-1)与tn-1及其之前所有时刻的电压都有关系。

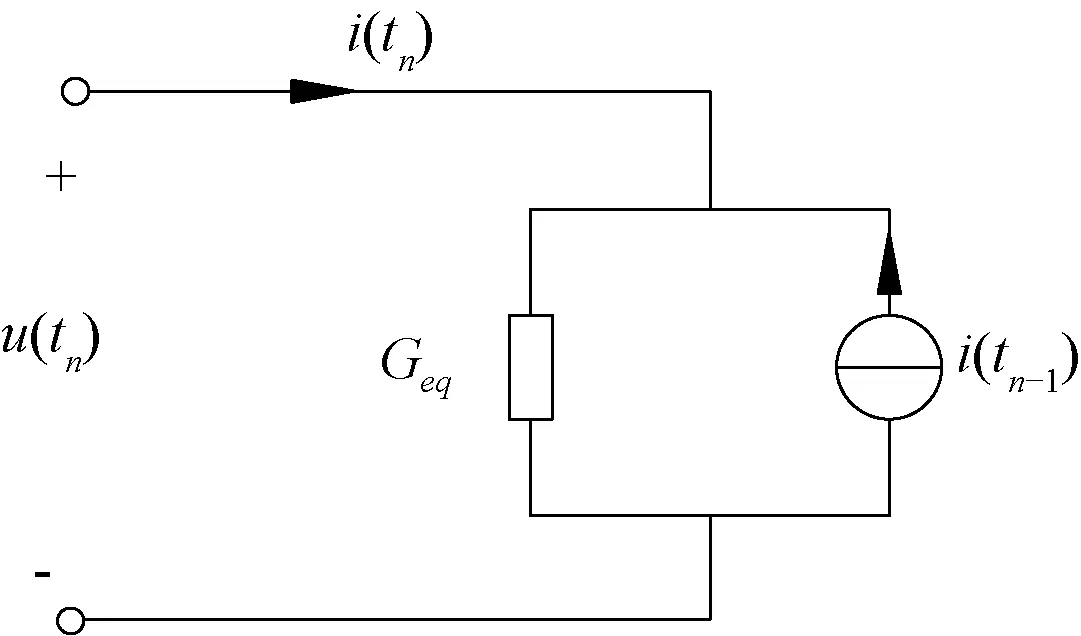
图1 分数阶电容的伴生模型Fig.1 The adjoint model of fractional order capacitance

同理，可得分数阶电感的离散伴生模型，其数学表达式为

(14)

2 分数阶电路实例分析

2.1 实例1

2.1.1 暂态分析

图2所示电路，已知电阻R1=R2=R3=1 Ω，电容值C=0.1 F，电感值L=0.1 H，分数阶电容值和阶次分别为Cα=0.1F/s0.5、α=0.5，分数阶电感值和阶次分别为Lβ=0.1H/s0.6、β=0.4。给定不同的电压源激励信号，0时刻将开关S合上，求各支路电压、电流。

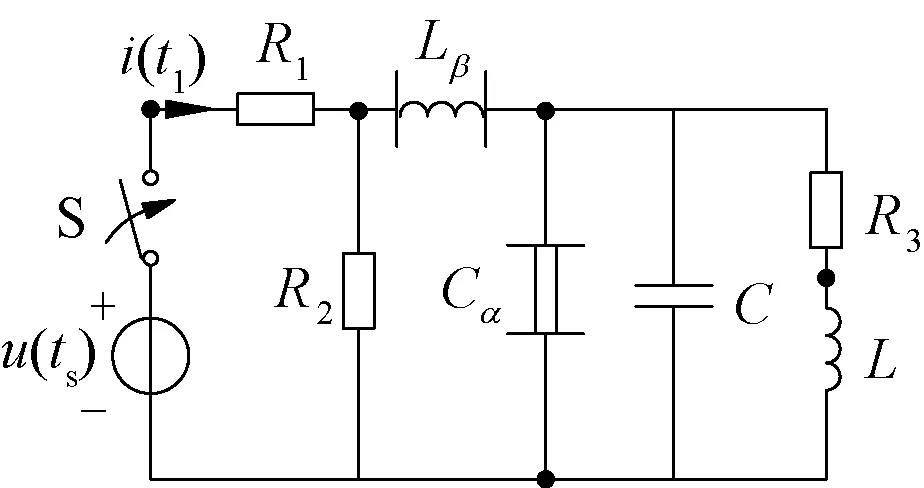
图2 实例1电路图Fig.2 The fractional order circuit of example 1

实例1电路的手工求解相当复杂，利用频域解进行分数阶数值逆拉式变换作为电路方程的精确解。步长Δt≤(5/k)×10-3s，k为信号变化最大斜率。

(1)当us(t)=10 V时，Δt=5×10-5s，分数阶电容两端的电压及其误差如图3所示。

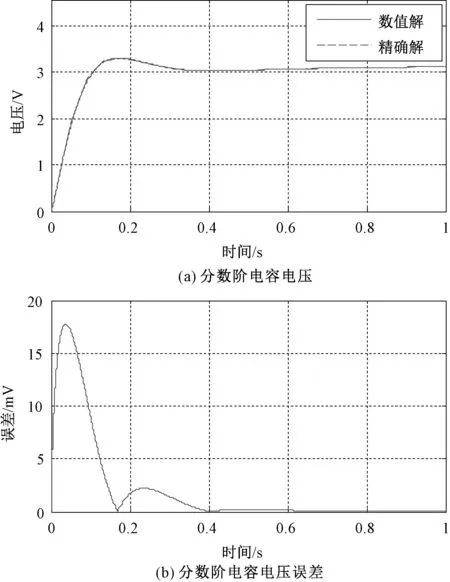
图3 分数阶电容电压及误差Fig.3 Voltage and its error of fractional order capacitance

(2)当us(t)=10sin(50t) V时，步长Δt=10-5s，分数阶电容电压及其误差如图4所示。

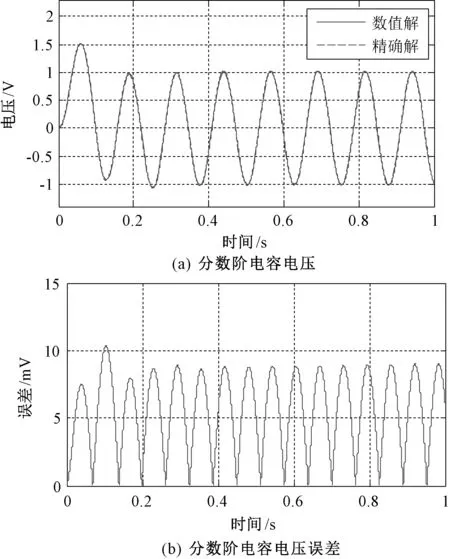
图4 分数阶电容电压及误差Fig.4 Voltage and its error of fractional order capacitance

(3)令R1=R2=R3=1 kΩ，C=0.1 μF，L=0.1 μH，Cα=0.1 μF/s0.5、α=0.5，Lβ=0.1 μH/s0.6、β=0.4。电压源为图5所示的单位阶跃信号，上升沿为1 ns，下降沿为0.5 ns，宽度为1 ns，其表达式为

(15)

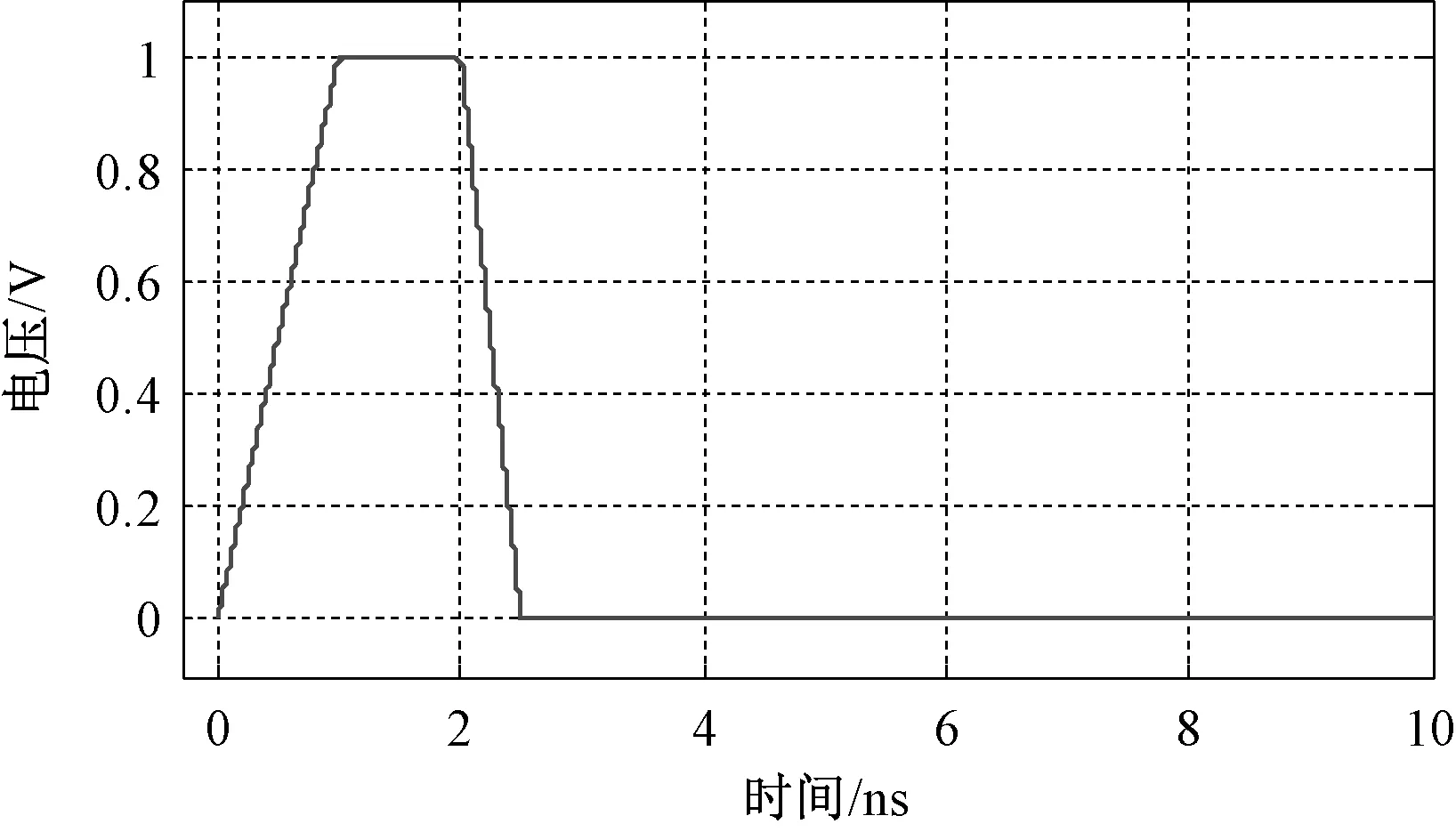
图5 单位阶跃信号波形Fig.5 The waveform of unit step signal

步长Δt=5×10-13s，分数阶电容电压及其误差如图6所示。

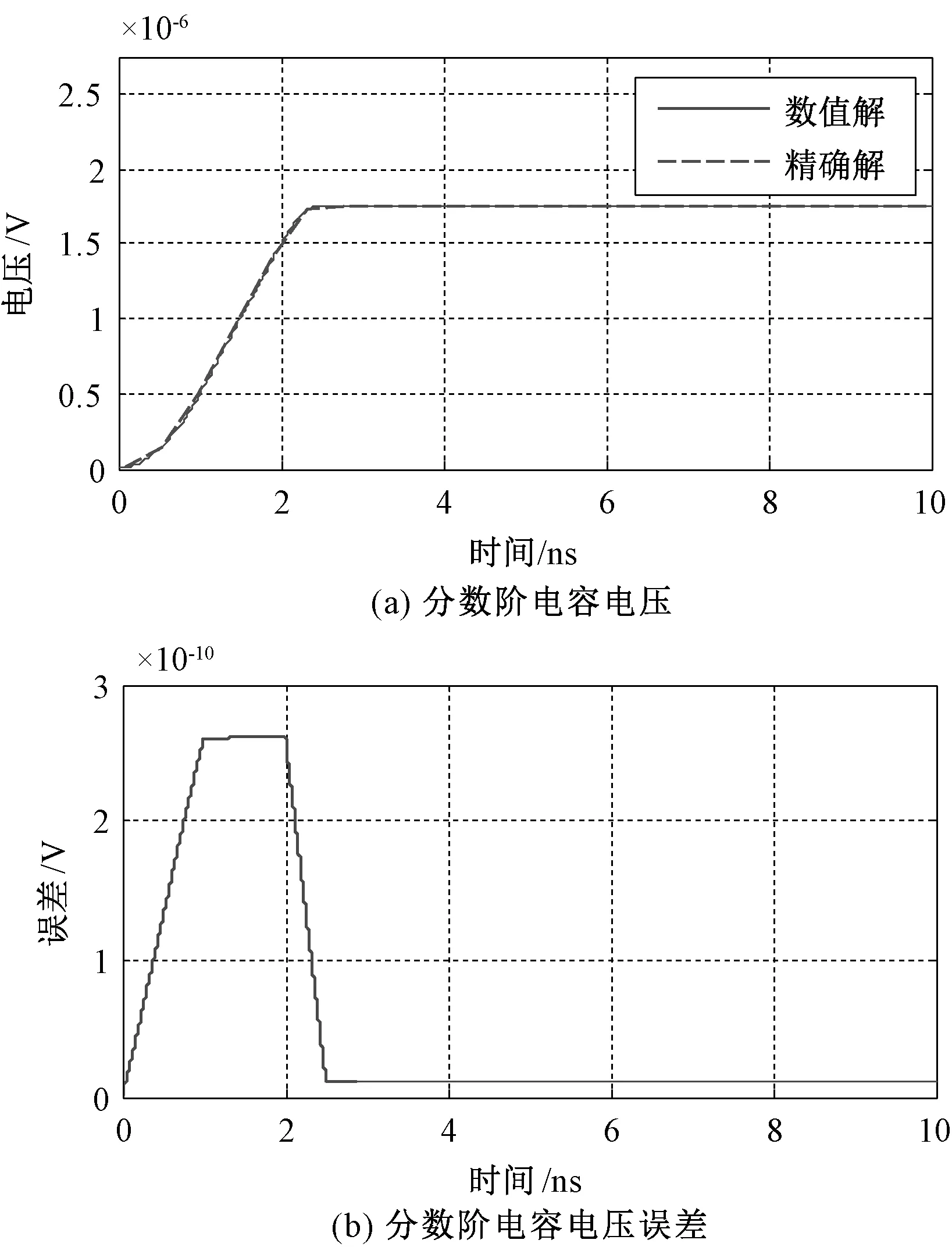
图6 分数阶电容电压及误差Fig.6 Voltage and its error of fractional order capacitance

(4)电压源为图7所示的复杂信号，其上升沿斜率k为6.199×1010，上升时间为3.161 ns。

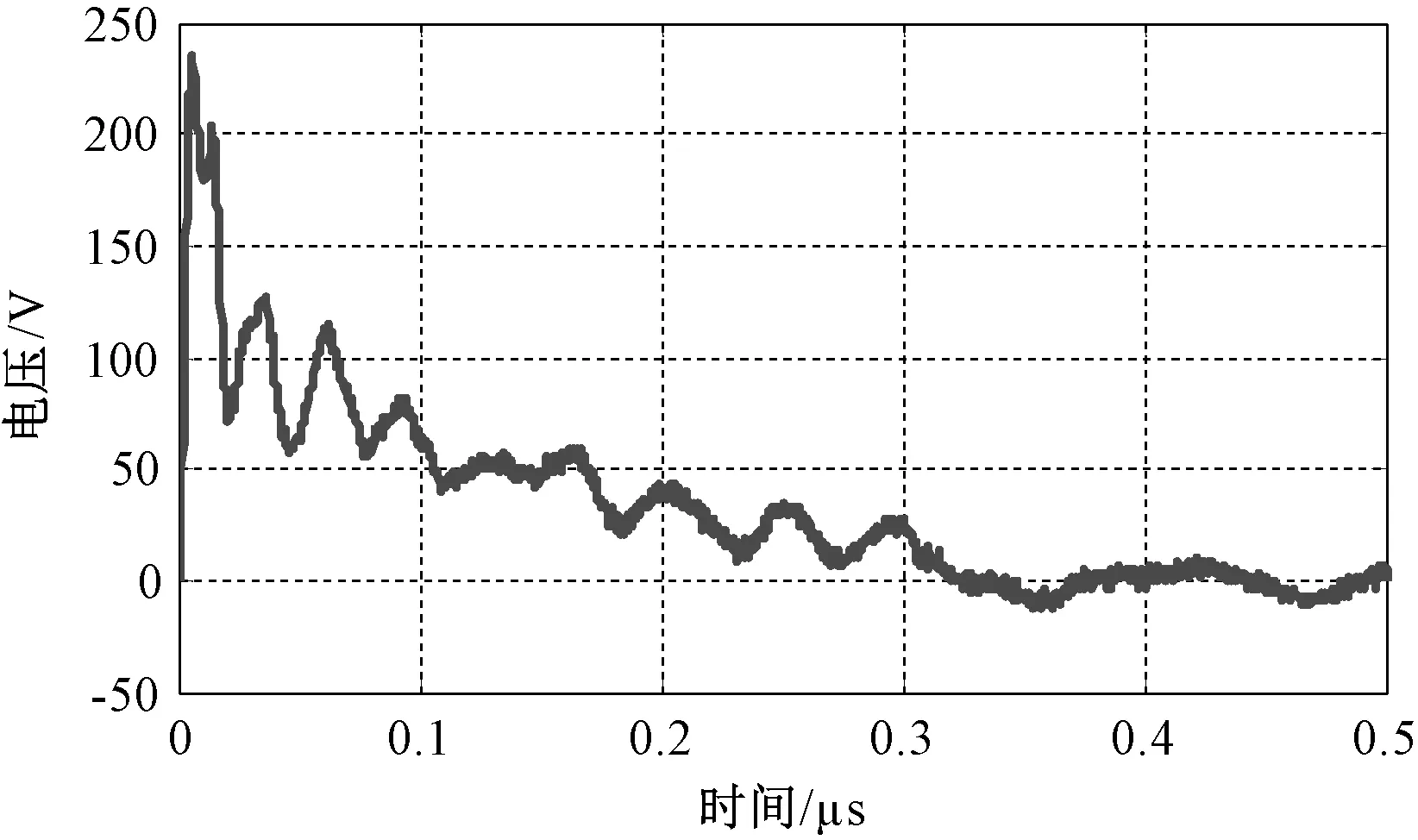
图7 复杂信号波形Fig.7 The waveform of complex signal

步长Δt=8×10-15s，电流i1(t)及其误差如图8所示，图中红色虚线为FFT所求精确解。

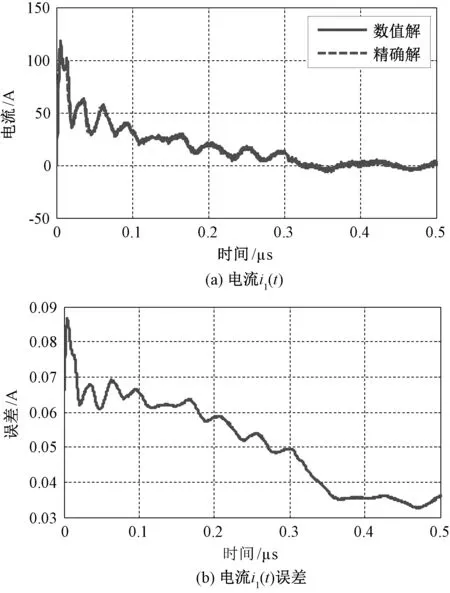
图8 电流i1(t)及误差Fig.8 Current and its error

2.1.2 稳态分析

图2所示电路各参数保持不变，开关S闭合后电路达到稳态，通用程序对稳态电路进行直流分析、交流分析。电压源为us(t)=10 V时，求得分数阶电容电压为3.333V。当us(t)=10sin(50t)V时，各支路电压、电流如图9所示，1～8为支路编号。

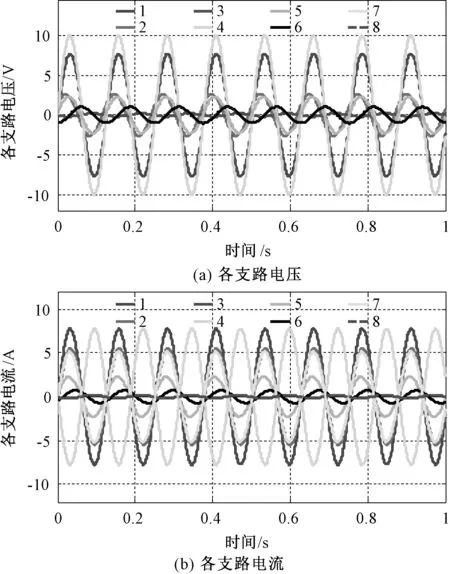
图9 各支路电压和电流Fig.9 Voltage and current of each branch

2.2 实例2

分数阶蔡氏电路[18,19]如图10所示，其中RN为非线性电阻，其电压、电流关系为

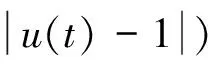
(16)

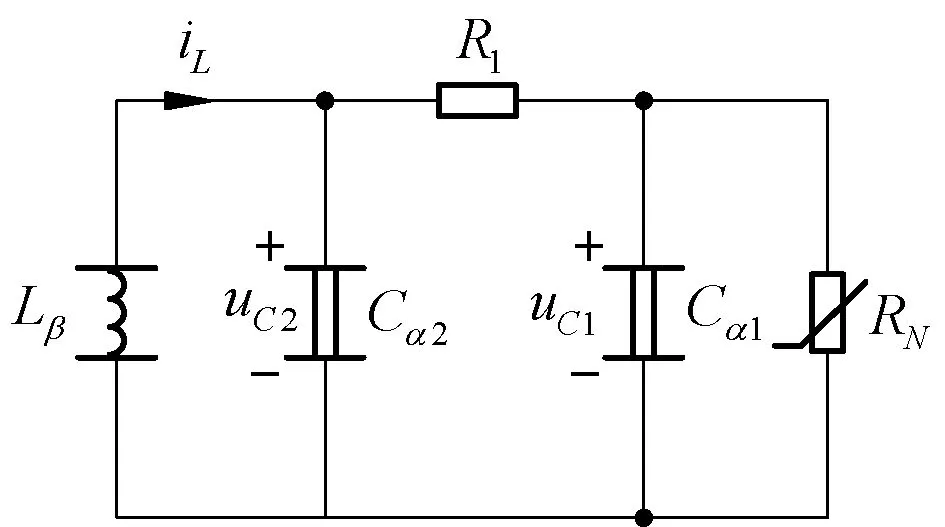
图10 分数阶蔡氏电路Fig.10 The fractional Chua’s circuit

已知α1=0.93，α2=0.99，β=0.92，R1=1 Ω，Cα1=1/10.725 F/s0.07，Cα2=1 F/s0.01，Lβ=1/10.593 H/s0.08，m0=-1.172 6，m1=-0.787 2，令x(t)=uC1(t)，y(t)=uC2(t)，z(t)=iL(t)，步长Δt=5×10-4，假设系统初始条件为：(x(0),y(0),z(0))=(0.2,-0.1,0.1)，此时会出现混沌现象，x(t)时域解及x(t)误差如图11所示。

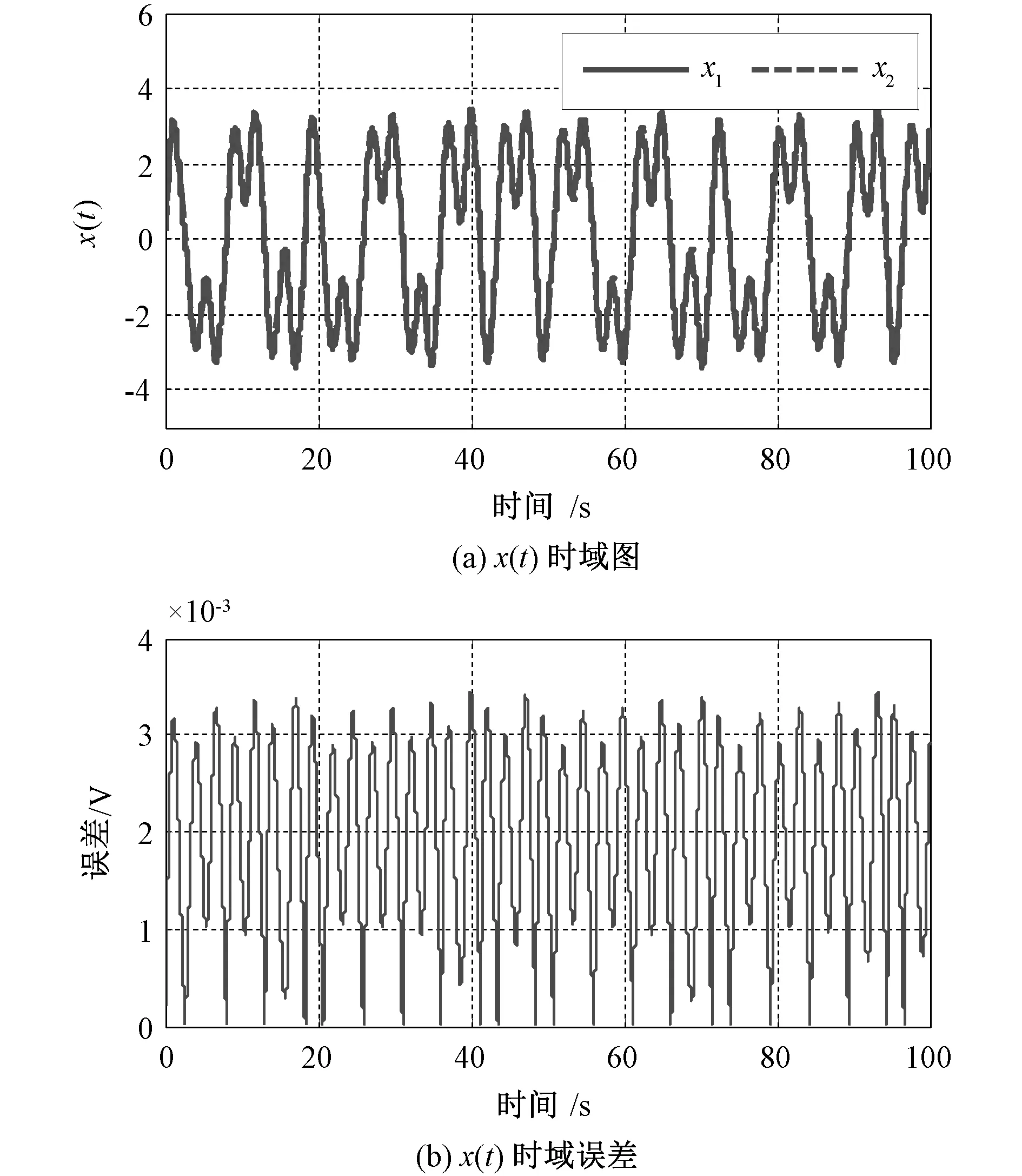
图11 x(t), y(t), z(t) 时域图及其误差Fig.11 Time domain waveform and its error of x(t)

图11(a)中x1和x2分别为本文程序和状态方程法所得x(t)时域波形，两波形基本吻合，分数阶蔡氏电路的吸引子如图12所示。

在一定参数条件下，分数阶蔡氏电路会产生双吸引子的混沌现象。本文程序所得波形与状态方程法的波形保持一致，因此可以分析含有非线性电阻的分数阶电路。

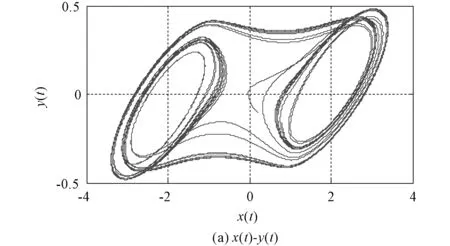
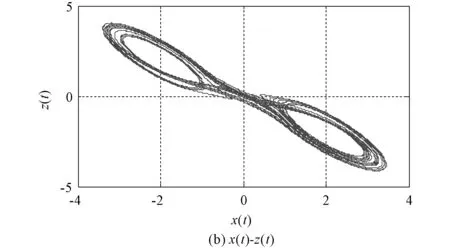
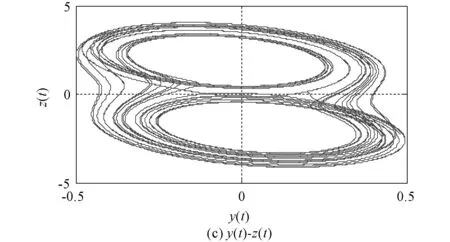
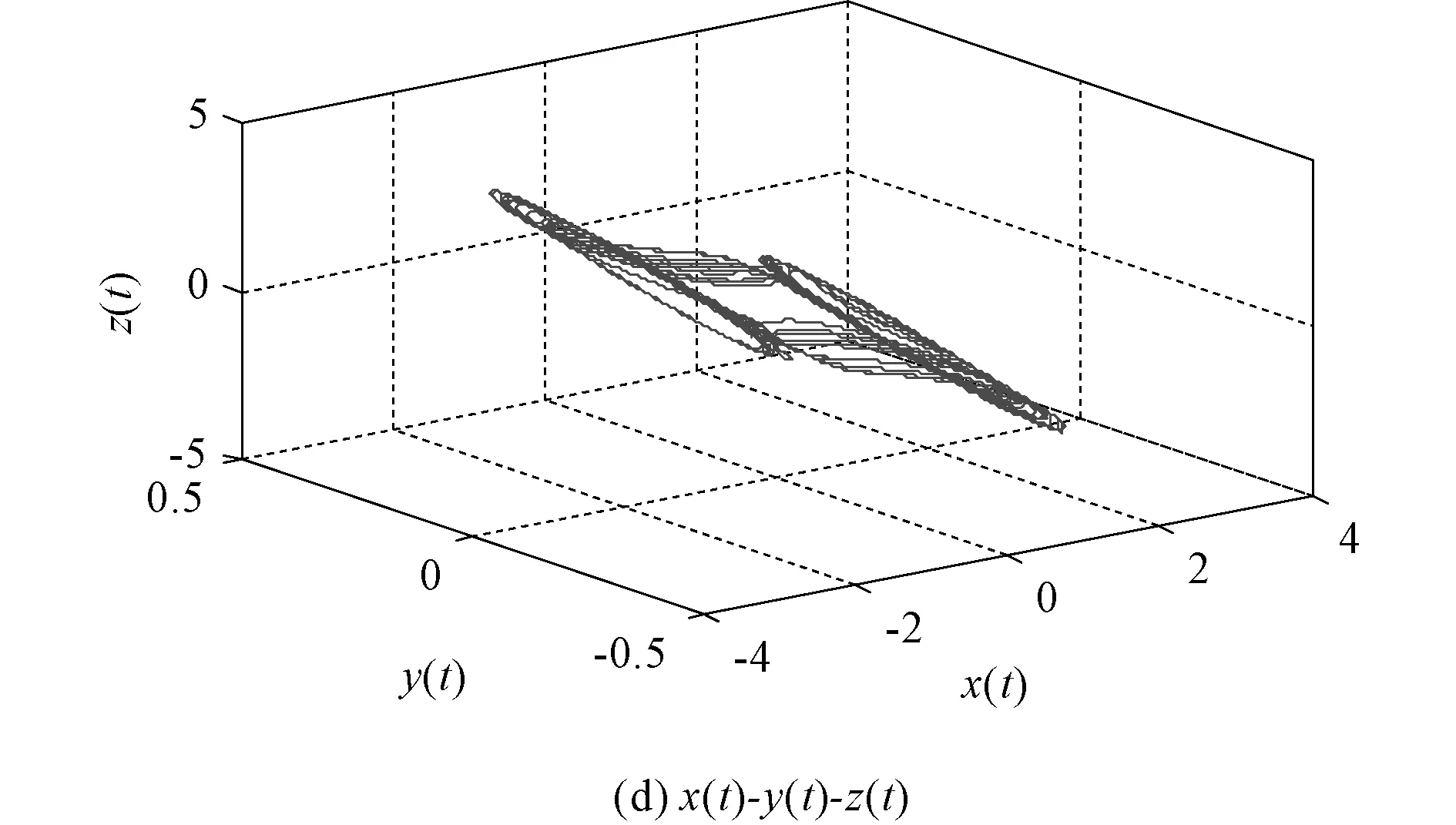
图12 分数阶蔡氏电路的吸引子图Fig.12 The attractors of fractional order Chua′s circuit

3 误差分析

实例1中，电压源为直流电压源时，Δt1=10-4，Δt2=5×10-5；电压源为正弦电压时，Δt1=2×10-5，Δt2=1×10-5；电压源为单位阶跃信号时，Δt1=10-12，Δt2=5×10-13。对三种电路分别取分数阶电容电压最大误差，如表1所示。

表1 分数阶电容电压最大误差

Tab.1 Maximum error of fractional order capacitance’s voltage

步长/s误差1/V误差2/V误差3/VΔt12540×10-21547×10-25115×10-10Δt21774×10-21034×10-22618×10-10

表1中误差1、误差2和误差3分别是电压源为直流信号、正弦信号、阶跃信号时的分数阶电容电压误差。由表1可知，误差随着步长的减小而减小。直流电路中电压误差最终趋向于0；正弦电路中电压在峰值处变化较慢，误差在峰值处较小；阶跃电路中，电压最大误差为2.618×10-10；复杂信号电路中，电流i1(t)的最大误差为0.086 6，占幅值的0.074%；分数阶蔡氏电路，通用程序得到的时域波形与各相波形与状态方程法所得到的波形保持一致。仿真结果表明，当Δt≤(5/k)×10-3s时，误差最大值与峰值比小于0.1%，满足精度要求。以上分析表明该程序可以分析任意线性分数阶电路和部分非线性分数阶电路，并可以通过控制步长以满足不同的精度要求。

4 结 论

基于Caputo导数的L1插值离散逼近法建立分数阶元件的伴生模型，通过仿真验证了该伴生模型的可行性与准确性，为电路分析软件提供了分数阶元件模型，对分数阶电路的发展具有重要意义。

本文程序可以对任意线性分数阶电路进行稳、暂态分析，还可以自动求解含有非线性电阻的分数阶电路，具有较强的通用性，为分数阶电路的计算机辅助分析提供了有效的辅助工具，一定程度上弥补了当前电路分析软件的不足。

[1] 刘崇新．一个超混沌系统及其分数阶电路仿真实验[J]．物理学报，2007，56(12)：6865-6873．

[2] 刘欣，崔翔，梁贵书，等．基于分数阶微分理论的宽频建模方法[J]．电工技术学报，2013，28(4)：20-27．

[3] 闫丽梅，祝玉松，徐建军，等．基于分数阶微积分理论的线路模型建模方法[J]．电工技术学报，2014，29(9)：260-268．

[4]PETRASI，SIEROCIUKD，PODLUBNYI．Identificationofparametersofahalf-ordersystem[J]．IEEETransactionsonSignalProcessing，2012，60(10)：5561-5566．

[5]MARTINR，QUINTANAJJ，RAMOSA，etal．Modelingelectrochemicaldoublelayercapacitor，fromclassicaltofractionalimpedance[J]．JournalofComputational&NonlinearDynamics，2008，3(2)：61-66．

[6]JESUSIS，MACHADOJAT．Developmentoffractionalordercapacitorsbasedonelectrolyteprocesses[J]．NonlinearDynamics，2009，56(1)：45-55．

[7]AHMADWM，SPROTTJC．Chaosinfractionalorderautonomousnonlinearsystems[J]．ChaosSolitons&Fractals，2003，16(2)：339-351．

[8]MACHADOJAT，GALHANOAMSF.Fractionalorderinductivephenomenabasedontheskineffect[J]．NonlinearDynamics，2012，68(1-2)：107-115．

[9] 杨华中，罗嵘，汪蕙．电子电路的计算机辅助分析与设计方法(第2版)[M]．北京：清华大学出版社，2008．

[10]MURIODA．Implicitfinitedifferenceapproximationfortimefractionaldiffusionequations[J]．Computers&MathematicswithApplications，2008，56(4)：1138-1145．

[11] 马龙，梁贵书，董华英．含分数阶电抗元件网络的灵敏度分析[J]．华北电力大学学报(自然科学版)，2013，40(3)：6-10．

[12] 袁晓．分抗逼近电路之数学原理[M]．北京：科学出版社， 2015．

[13]MEERSCHAERTMM，TADJERANC．Finitedifferenceapproximationsforfractionaladvectiondispersionflowequations[J]．JournalofComputational&AppliedMathematics，2004，172(1)：65-77．

[14]TADJERANC，MEERSCHAERTMM,SCHEFFLERHP.Asecond-orderaccuratenumericalapproximationforthefractionaldiffusionequation[J]．JournalofComputationalPhysics，2006，213(1)：205-213．

[15]ALIKHANOVAA．Anewdifferenceschemeforthetimefractionaldiffusionequation[J]．JournalofComputationalPhysics，2014，280(C)：424-438．

[16]GAOGH，SUNZZ，ZHANGHW．AnewfractionalnumericaldifferentiationformulatoapproximatetheCaputofractionalderivativeanditsapplications[J]．JournalofComputationalPhysics，2014，259(2)：33-50．

[17] 孙志忠，高广花．分数阶微分方程的有限差分方法[M]．北京：科学出版社，2015．

[18]ALKAHTANIBST．Chua'scircuitmodelwithAtanganaBaleanuderivativewithfractionalorder[J]．ChaosSolitons&Fractals，2016，89：547-551.

[19]HARTLEYTT，LORENZOCF，KILLORYQAMMERH．ChaosinafractionalorderChua'ssystem[J]．IEEETransactionsonCircuits&SystemsIFundamentalTheory&Applications，1995，42(8)：485-490．

Research on Discrete Adjoint Models and Simulation Calculation of Fractional Order Elements

LIANG Guishu, SHAN Dongqing

(School of Electrical and Electronic Engineering, North China Electric Power University, Baoding 071003, China)

By comparing a variety of implement methods of fractional order elements, the discrete adjoint models of fractional order elements are established with the approach of L1 interpolation approximation. The feasibility and accuracy of the discrete adjoint model of fractional order elements are verified by simulation calculation. A general program for analyzing fractional order circuits is written by the sparse tabular method. This program facilitates the automatic solution of arbitrary linear fractional order circuits and partial nonlinear fractional order circuits, which can be used as an auxiliary tool for analyzing fractional order circuits, thus making up the deficiency for the existing software’s inability of simulating the fractional order circuits.

fractional order elements; adjoint models; fractional order circuits; sparse tabular method; automatic solution

10.3969/j.ISSN.1007-2691.2017.03.01

2016-07-15.

国家自然科学基金资助项目(51177048，51407073)；河北省自然科学基金资助项目(E2012502009).

TM13

A

1007-2691(2017)03-0001-07

梁贵书(1961-)，男，教授，博士生导师，研究方向为电网络理论及其应用，电力系统电磁兼容和电力系统过电压及其防护；单栋清(1990-)，男，硕士研究生，研究方向为电网络理论及其应用。