控制草原鼠患的评价模型
官金兰,陈芷棋,聂国康,林晓佳
(广东农工商职业技术学院基础部,广东广州510507)
控制草原鼠患的评价模型
官金兰,陈芷棋,聂国康,林晓佳
(广东农工商职业技术学院基础部,广东广州510507)
为了解决鼠患问题,使用灭鼠药、引入天敌、人工种植牧草等三种方法进行模型分析。模型一:由于使用灭鼠药,导致老鼠数量增长会受到阻滞。在logistic模型上使用时间与灭鼠药用量的变量,用Matlab求解;模型二:将老鼠称为食饵,引入的天敌称为捕食者,二者共同组成P-P系统,可建立Volterra模型分析出老鼠和天敌数量的平衡点;模型三:引入人工种植牧草的阻滞系数,分析牧草生长阻滞系数和时间的关系,通过Matlab求解。
logistic模型;微分方程;Volterra食饵-捕食者模型
在内蒙古大草原,由于各种人为因素对自然生态系统的破坏(如过度放牧、大量消灭草原上的狼群等),从而造成草原鼠患问题非常严重,并由此引发了严重的生态问题[1]。由于老鼠有挖掘的习性,在所有鼠害发生的地方,洞道纵横,水土流失严重,有的甚至形成了大面积寸草不生的“鼠荒地”。然而人们至今尚未找到能有效控制进而消灭草原老鼠的办法。也就是说,至少以目前的技术力量,还不能用人工种草的办法永久地恢复自然植被。
建立老鼠自然状态下的生长模型,若老鼠的数量达到一定值时不加以控制,将会对生态环境造成严重的危害,因此笔者分析提出以下三种方法并建立模型,同时对其短期和长期的效果进行评估分析,在资金投入最少的情况下达到控制草原鼠患,恢复生态平衡的效果。
为了控制草原的鼠患,人们采用了以下几种方法:
(1)灭鼠药。研制无公害的灭鼠药,但这需要一定的时间和大量资金投入。
(2)引入老鼠的天敌。通过人工喂养和驯化老鼠的天敌来控制鼠患,这种方法在短期内有效,但存在两个问题:第一,费用比较高;第二,引入数量难以确定。
(3)人工种植牧草。在草原植被密集的地方,老鼠不易于打洞且难于及时躲避天敌的追捕,但据知几乎所有的人工种草都会在一定时间内自行退化。
1 控制草原鼠患模型的假设与建立
1.1 模型假设
(1)老鼠的出生率和死亡率不变;
(2)草原的面积为10 000万公顷;
(3)短期内老鼠的体内不产生抗体;
(4)草原上老鼠的天敌数量可忽略不计;
(5)草原自然环境相对稳定;
(6)人工种植牧草成活率为100%。
1.2 符号说明
模型中所用到的参数及变量的单位均为国际单位,符号说明见表1。

表1 符号说明
1.3 模型的建立
1.3.1 模型一的建立
在自然生长状况下,草原生态系统严重失调,老鼠天敌的数量可忽略不计,此时老鼠的数量以几何级数增长,当增长到一定程度时,由于环境因素及资源的影响,老鼠的数量达到了环境容纳量的最大值。这种情况下老鼠的生长模型基本符合logistic模型[2]。设r为老鼠的自然增长率,N为草原老鼠的环境容纳量,建立如下模型
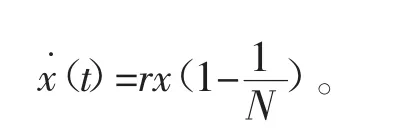
取r=0.5,N=100 000,用Matlab求解,结果如图1所示。
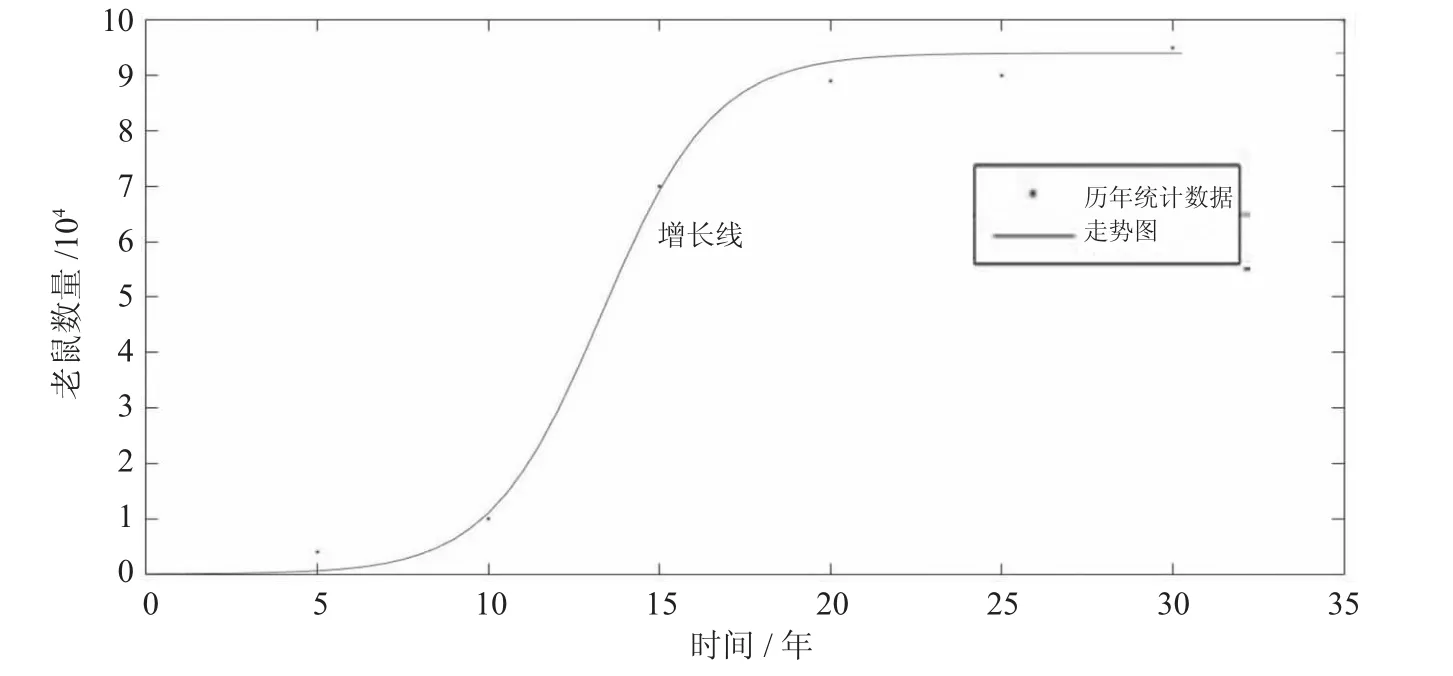
图1 使用灭鼠药前老鼠数量变化曲线
使用灭鼠药时,设d为灭鼠药对老鼠的致死率,当t=t0时,x(t0)=N,得
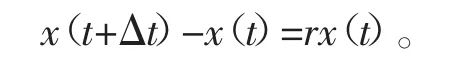
在灭鼠药的作用下,老鼠数量的变化函数为

化简此方程组得

用Matlab求解,结果如图2所示。
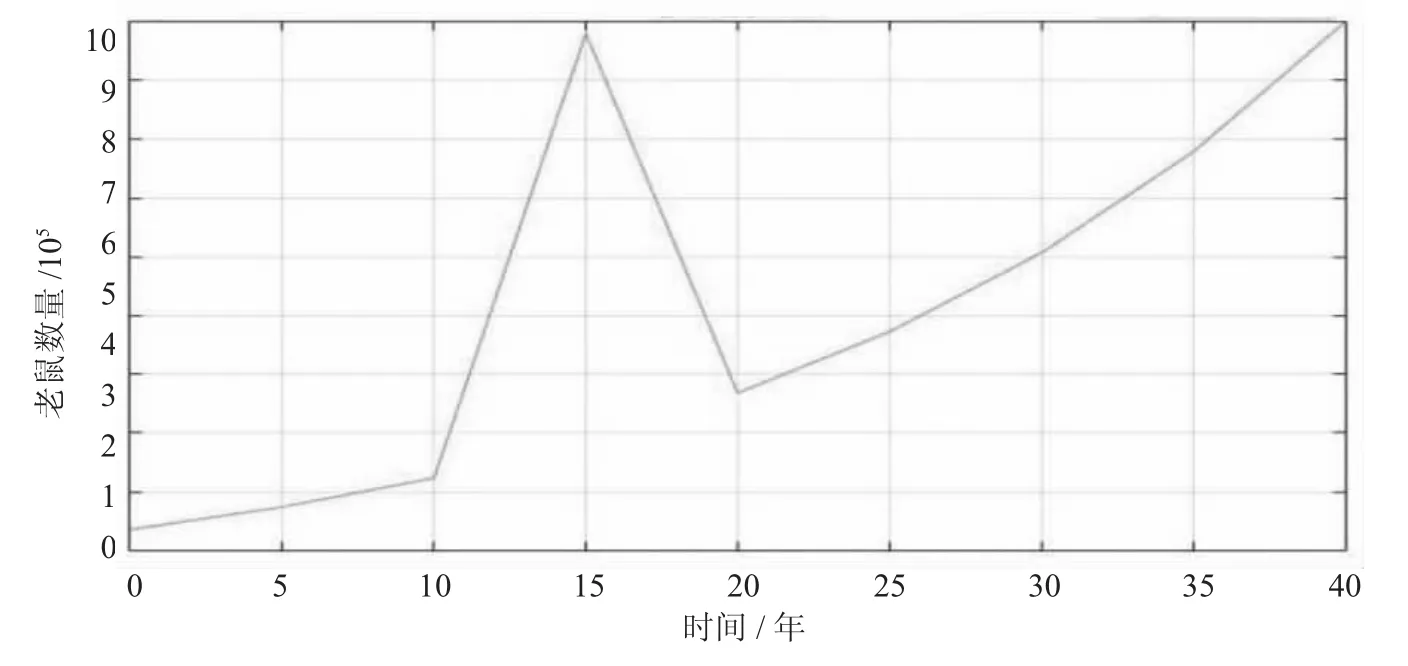
图2 使用灭鼠药后老鼠数量变化曲线
由图1、2可知,在未使用灭鼠药之前老鼠的数量呈上升趋势,使用灭鼠药后在一定时间内老鼠的数量逐渐减少。
设M为杀死每只老鼠所需灭鼠药的药量,p1为灭鼠药的单价,投入的资金为
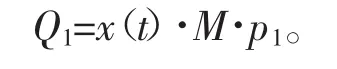
1.3.2 模型二的建立
设老鼠的数量为x(t),天敌的数量为y(t),a为天敌掠取老鼠的能力,b为老鼠供养天敌的能力,建立如下模型[3]

当引入天敌时,老鼠的增长率下降,老鼠使其天敌的死亡率减少,减少量与y成正比,则

其天敌独立生存的死亡率为d,即

老鼠使天敌的死亡率减少,减少量与x成正比,即

由方程(1)、(2)知方程的平衡点为
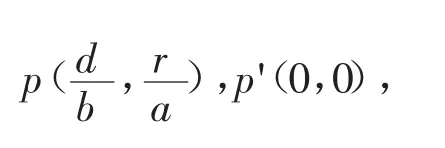
从方程(1)、(2)消去dt后得到

这时可分离变量方程,写作
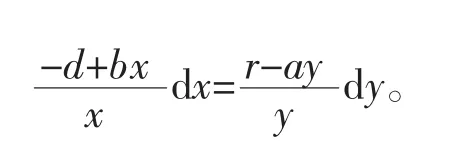
由上述方程得(1)、(2)的相轨线为

将相轨线的极值点记为x0,y0,极大值记为fm,gm。
因为

当c>fmgm时无相轨线;当c≤fmgm时相轨线是封闭曲线,由此可以确定天敌投入数量,以免过多或者过少。
设n为引入天敌的数量,p2为天敌的单价,所以投入资金Q2=np2。
1.3.3 模型三的建立
在logistic模型的基础上引入牧草影响的阻滞系数m。由于牧草自身的生长状况,m会随时间变化而变化,建立如下模型[4]

设买入牧草种子为α斤,通过Matlab进行拟合,可得图3。
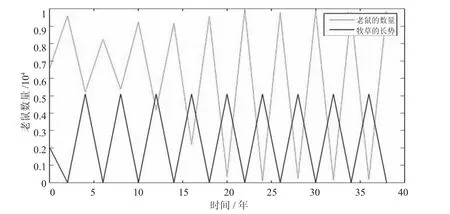
图3 人工种植后老鼠数量随时间变化趋势图
由图3可知,在牧草生长时期老鼠的数量会缓慢上升,当牧草越长越茂盛时,牧草对老鼠的抑制作用越来越强。当牧草退化时,老鼠的数量逐渐上升。投入的资金为Q3=α·p3。
2 模型的相关分析
模型一使用灭鼠药在短期内能对老鼠的数量起到一定的遏制作用,但长时间后老鼠的体内产生了抗体,对灭鼠药会产生抵抗作用。
模型二引入老鼠的天敌能控制老鼠的增长速度,但是需要花费大量的时间和金钱,从长期效果来看是一种不错的选择。
模型三种植牧草在刚开始时由于牧草比较小,不茂密,很容易被老鼠吃掉,在短时期内很容易遭到破坏。
3 相关建议的提出
考虑到三种方法的各自优势及长短期效应,笔者建议在种草最佳时机靠前一段时间投放鼠药(有一个最佳投放量),初见药效随之种草,在药效衰减到不能间接危害到老鼠天敌的时候引入天敌来灭鼠。
第1步,使用老鼠药的成本较其他两种方法而言低得多,事先使用老鼠药可使总成本降低;第2步,待老鼠药灭鼠见成效后应种植牧草,鼠类是一种需要开阔视野的生物种,只要有茂密的牧草生长,它们就无法生存;第3步,引入老鼠的天敌,此时残余的老鼠药不会对天敌造成间接的伤害。适当引入天敌数量可使天敌与牧草共同发挥作用,控制老鼠天敌的数量,从而达到新的生态平衡,限制草原老鼠在一个不能形成鼠患的范围之内。
4 模型的评价
上述模型在一定时期内可以反映灭鼠方法的成效,通过模型的建立,本文提出了切实可行的建议。但是,考虑的因素比实际的相对少一些,没有对模型进行定量的分析。
[1]刘得元.草原灭鼠的现状及对策[J].家畜生态,2003(5):79-80.
[2]王兵团.数学建模基础[M].北京:清华大学出版社,2004.
[3]姜启源.数学建模[M].3版.北京:高等教育出版社,2003.
[4]孙军娜.控制草原鼠患模型[J].安徽农业科学,2012,40(12):7147-7150.
【责任编辑:王桂珍 foshanwgzh@163.com】
Evaluation model of rodent control in prairie
GUAN Jin-lan,CHEN Zhi-qi,NIE Guo-kang,LIN Xiao-jia
(Department of Basic Course,Guangdong AIB Polytechnic College,Guangzhou 510507,China)
In order to solve the problem of rats,this article makes use of three methods to analyze model,the methods are as follow:usingrodenticide,leading into natural enemies,planting grass artificially.The first model: the rats will be influenced by the law of block growth because of rodenticide-the law of logistic.In the logistic model,we use the variables of time and dosage of rodenticide to solve by Matlab.The second model:the rats-prey and the natural enemies-predator make up P-P system,which can be established Volterra model to find out the equilibrium point of rats and natural enemies.The third model:for the sake of gaining the relationship of pasture growth’s coefficient and time,we introduce the retardation coefficient of artificial pasture and solve byMATLAB
logistic model;differential equation;Volterra prey-predator model
S443
A
1008-0171(2017)03-0023-05
2016-09-21
广东省大学生攀登计划培育项目(pdjh2016b0653)
官金兰(1982-),女,广东韶关人,广东农工商职业技术学院副教授,博士。
——管氏肿腿蜂的应用技术
——黔南扁穗雀麦

