基于Map Reduce的云数据挖掘模型的设计与实现
◆谢 光
基于Map Reduce的云数据挖掘模型的设计与实现
◆谢 光
(三亚学院 海南 572000)
当今社会随着计算机技术的高速的发展,涌现出大量的数据,促使了云数据逐渐成为时代潮流。数据挖掘技术则正是从这些大量的数据中提取对我们有价值的的数据。数据挖掘又叫做数据采矿、数据资料探勘等,是当今数据快速发展的产物。大数据的出现对传统的简单的数据挖掘算法提出挑战,新型的基于Map Reduce的云数据挖掘正在茁壮地发展。Map Reduce是当前最流行的分布式计算模型,在云数据数据挖掘当中作为一个佼佼者迅速发展。本文主要研究传统的数据挖掘算法如何与Map Reduce计算模型有效地在云数据中结合起来。给当今云数据挖掘模型做出了较好的阐述。
云数据;数据挖掘;分布储存系统;Map Reduce
0 引言
Map Reduce计算模型[1]是目前数据挖掘处理中最流行的一种云计算环境下的分布式计算模型[2-3],它可以将所有的数据处理均匀地分布在不同的计算机上,并且可以同时屏蔽复杂的并行编程,将所有处理的编程处理归结到两个简单的函数,这两个函数就是map函数和reduce函数[4],这两个函数有着可用性、高可扩展性、高容错性及简单性使得其数据挖掘工作变得更加容易、更加简便。为了使得Map Reduce模型适用于数据量更大的数据挖掘,本文对数据挖掘原有的算法进行了改进,提出了基于Map Reduce的K-means算法模型,对K-means算法模型进行Map Reduce化。
1 数据挖掘
数据挖掘(Data Mining),是处理大量数据库的一种软件。主要职责就是从大量数据中获取有效的、新颖的、潜在有用的、最终可理解的模式的非平凡数据发现过程。简单的说,数据挖掘就是从大量数据中提取或“挖掘”数据中有用的信息[5]。
Map Reduce最先是由Google公司设计出来的,并且一贯成为Google公司的核心计算模型,它也是一种程序模型,将复杂的运行于大规模集群上的并行计算过程高度的抽象到了map函数和reduce函数这两个函数[6],主要用于数据集大于1TB的并行运算,现如今也大量的应用在云数据的数据处理上。Map函数接受一组数据并将其转换为一个键/值对列表,输入域中的每个元素对应一个键/值对。Reduce函数接受Map函数生成的列表,然后根据它们的键(为每个键生成一个键/值对)缩小键/值对列表[7]。根据这一性质可以得到Map Reduce的流程概念图如图1所示。
根据MapReduce的核心思想得出MapReduce模型[8]的主要流程图如图1所示,对流程图进行分析并且进一步总结可以得出Map Reduce还有几个比较重要的特点,主要在数据分布储存、分布式并行计算、本地计算三个方面有着突出的表现:
(1)数据分布存储:Map Reduce模型由Google公司采用GFS的底层文件系统支撑。GFS主要是从不同的计算机当中获取的数据集群。然后很自然的将数据分布存储在GFS上,其实是存储在GFS的集群中各自的机器的本地磁盘中。
(2)分布式并行计算:Map Reduce其实质上是一种分布式的并行计算,但是其实际操作的是一个map和reduce函数,这两个函数对于各个数据分片,都会有一个Map任务(运行Mapper类的进程)对该分片进行处理,这种处理传承了良好的并行的方式。但是对同一个分片,Map Reduce的Map任务对该分片的
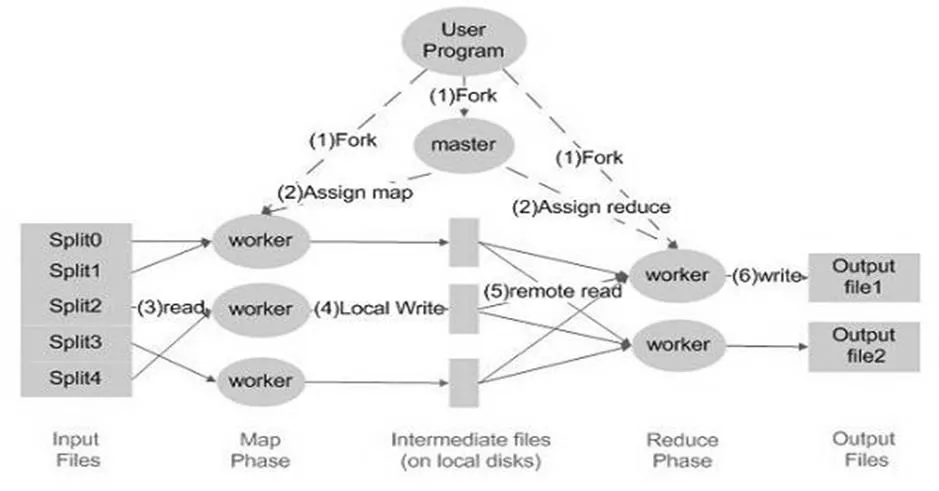
图1 Map Reduce模型主要流程
(3)本地计算:由于分布式系统中网络I/O的性能通常要比本地I/O的性能差,所以Map Reduce认为“移动计算比移动数据更经济”,即通过将计算任务派送到数据所在节点来实现本地计算。
2 基于Map Reduce云数据数据挖掘系统的设计与实现
2.1Map Reduce架构
在云数据数据挖掘中,Map Reduce 同样可以采用 Master/Slave 主从结构,根据Map Reduce的核心思想可以设计得到Map Reduce 架构主要包括Client、Job Tracker、Task Tracker 和 Task这四个组件。
2.2基于Map Reduce的数据挖掘
Map Reduce 是一种非常适合处理数据量很大,并且计算过程简单的并行计算框架,将Map Reduce 应用于数据挖掘领域是应对大数据挖掘难题的一种需求,是当今社会云数据出现后解决数据问题最简单的一个方式。2006年,在 NIPS 国际会议上提出一种称为“求和范式”条件,这种条件很明确的指出:一个数据挖掘算法能用 Map Reduce的基本要求。[9]

图2基于Map Reduce的云数据数据挖掘模型
3 K-means算法
K-Means算法是以K为参数,把数据集内的N个数据元组分为K个子集,以使得子集内的所有数据元组具有较高的相似度,且子集之问的数据元组的相似度较低。而相似度则是根据子集内对象的平均值来进行计算的[9]。K-Means算法的基本过程为:首先在全体数据集内任意选取K个数据元组作为初始的聚类中心,数据集内剩下的其他数据元组,则计算其与聚类中心的相似度(根据需要事先确定的某种欧氏儿何距离),依次将它们分别划归到与之最为相似(聚类中心的代表元组)的一个聚类中,再重新计算每个归并之后获得了新数据元组的新的聚类中心(新聚类所有数据元组的均值);并重复上述过程直到预先指派的某个测度函数(一般是均方差函数)收敛到某个阑值为止[10]。
3.1K-means算法聚类分析距离D的计算方法[11]
K-means算法的优点是原理简单,算法过程中的大部分计算来自于数据与聚类中心的距离计算与新的聚类中心的迭代过程。通常算法中的距离计算都是基于向量的。根据所选K-means算法的核心意义不同可以有以下四种不同的计算方法:
(1)余弦距离
两个向量之间的夹角的余弦值即为余弦距离,余弦距离与两个向量之间的夹角成反比关系。两个n维向量的余弦距离如下公式1所示。
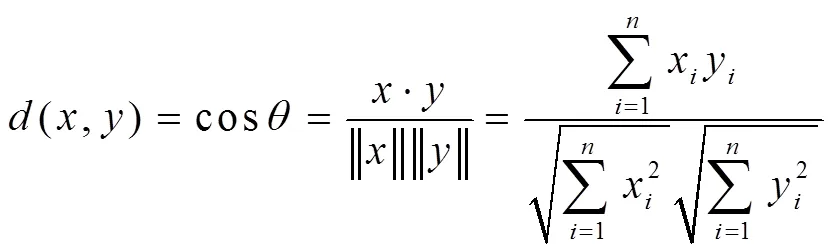
(2)欧几里得距离
欧式距离是测量的是n维空间中每个点之间的绝对距离。欧几里得距离计算公式2如下所示。
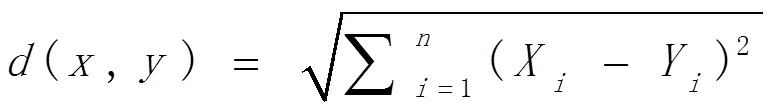
(3)曼哈顿距离
曼哈顿距离主要是两个点在标准坐标轴上的绝对轴距总和,曼哈顿名字主要是从网格状的城市区建筑块得来,在知道每个维度距离的同时,我们可以使用曼哈顿距离计算得到。两个n维向量的曼哈顿距离如下公式3所示。
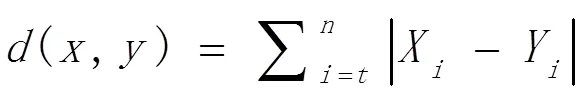
(4)Tanimoto距离
余弦距离没有计算到向量的权值,需要反映向量之间的角度就要使用Tanimoto距离。Tanimoto距离同时又叫Jaccard距离,角度和点之间的相对距离是我们通过Tanimoto距离所要得到多少数据。两个n维向量的Tanimoto距离如下所示。
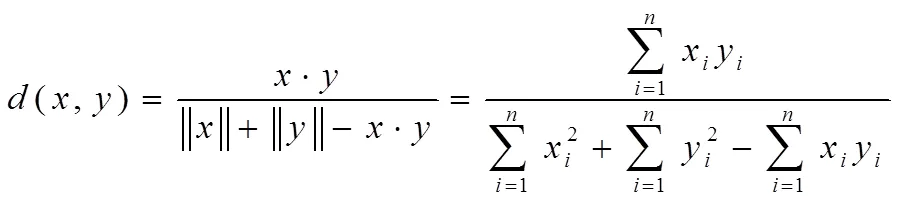
3.2 K-Means算法的Map/Reduce化
基于经典K-Means算法,探讨其云计算化中Map/Reduce化后K-Means算法的方案并进一步研究云计算化后的算法性能是本次研究的关键[12-13]。 Map/Reduce化后K-Means算法的执行步骤如下:
(1)随机选择k个初始聚类中心,如cp[0]=D[0],cp[k-1]=D[k-1],然后将这些聚类中心中的初始聚类数据复制到OriginalCluster[]中,并将OriginalCluster[]进行分块处理,根据计算节点集群的情况,将OriginalCluster[]块分配给各个计算节点;
(2)Map:对于D[0]…D[n]这些数据中,需要分别计算出cp[0]…cp[n-1]之间的距离,距离最近者记为c[i], c[i]的总个数可以用Ci表示,同时在Map/Reduce框架下,把键值分别对应到i、D[k]上;
(3)Reduce:由于i是Map/Reduce框架中键值对的Key,这保证了同一个Key的所有D [k]会分配到同一个Reduce进程,则在此Reduce进程可以计算新的聚类中心cp[i]=(Ec[i]对应的D[J])/Ci,并将此新的聚类中心存入DestinationCluster[];
(4)比较DestinationCluster[]与OriginalCluster[]这两个处理方式之间的变化,如果两者的变化小于预先给定值,则聚类完成,否则将DestinationCluster[]复制到OriginalCluster[]后继续重复上诉过程执行。
可以看出,K-Means算法的Map/Reduce化算法的改进之处,这是因为Map/Reduce框架是一致不变的,开发人员所要做的工作只是将算法可供Map和Reduce的部分剥离出来,构造键值对,其他调度、监控、通讯等任务就全部交由Map/Reduce框架去完成了。
4 实验仿真与分析
论文研究的是K-Means数据挖掘算法MapReduce化的可行性及过程,通过对实验形式论证其可行性。云计算是为海量数据的分析及处理而准备的,因此实验数据应具备如下特点:(1)海量的数据。只有数据规模达到一定的量才能达到本次实验的目的;(2)所选的数据集中所有的数据其属性、状态符、都应该符合K-means数据挖掘算法的Map Reduce化的要求。依次测试Map/Reduce化后挖掘算法的实际工作能力。
本文选取QQ音乐上某电台的一个媒体库作为实验数据集,数据集内包含音乐、歌曲、片头、片花、广告、音效、混合媒体包等媒体文件共110万条数据记录,同时包含电台听众点播记录600万条,网络互动消息记录2000万条[14-15]。
4.1实验结果分析
第一组实验使用的是数据集中网络互动消息记录中提取出来的1000万条数据,配置DataNode上的Reduce节点数为1, Map节点数分别为:1, 2, 5, 10, 100。K-Means算法的耗时分别为:612s, 466s, 307s, 163s, 199s。根据数据可以很直观的表示Map节点和耗时关系图如下图3所示:
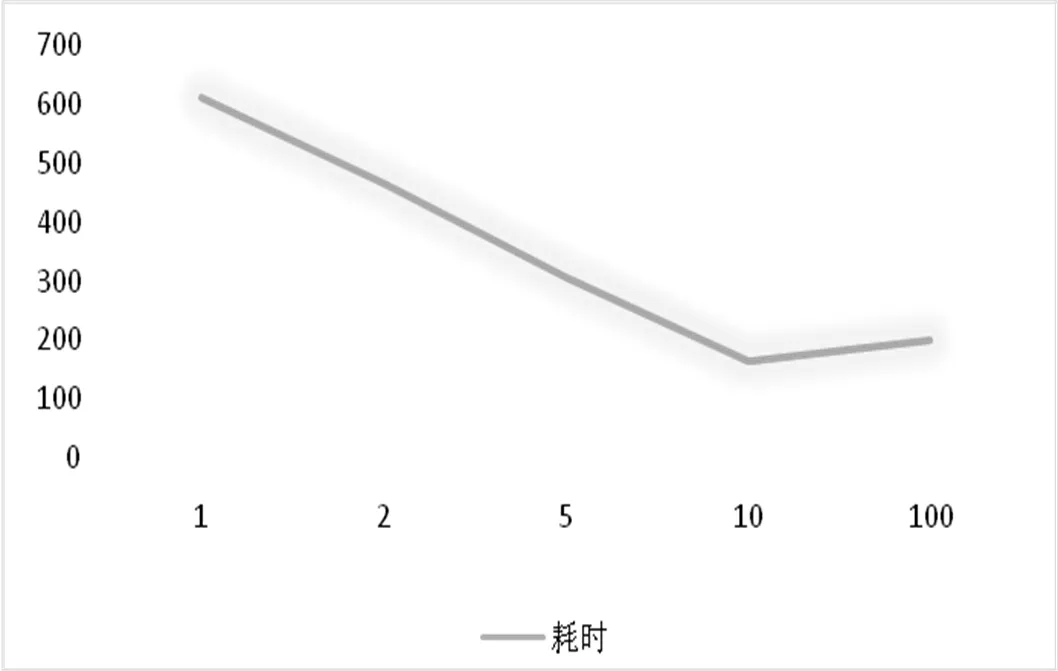
图3 Map节点和耗时关系图
根据图像很容易看出Map节点和耗时情况的关系,在Reduce节点为1的基础上,从数据中可以得出map节点在10的时候其运行效率最高。
第二组实验使用所有的数据集,配置DataNode上的Reduce节点数为1, Map节点数始终为10,而分别使用100万、500万、1000万、1500万、1800万、2000万条数据进行运算。K-Means算法的耗时分别为:66s,169s, 288s, 352s, 429s, 475s。根据数据得出不同数据量运算和时间关系图如图4所示:
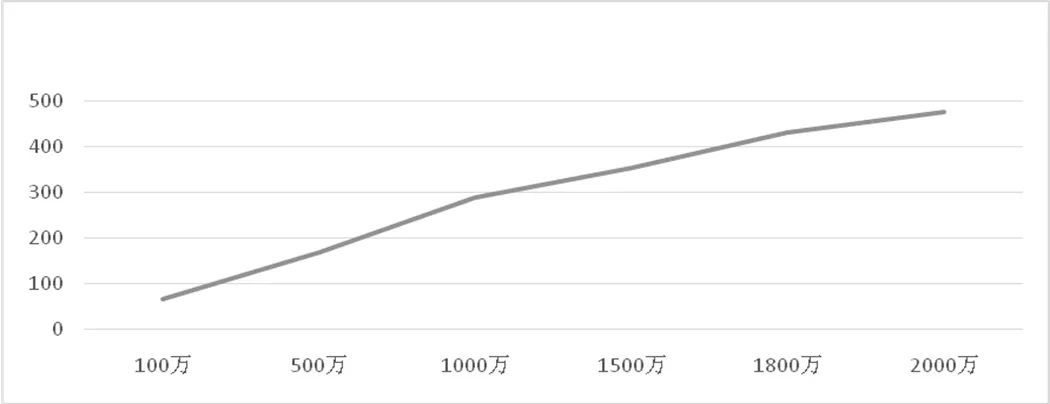
图4数据量和时间关系图
从图4图表信息中我们可以得出,Map节点数不变的时候,随着数据量的增加耗时也会逐渐增加。两者之间成正比关系。
4.2 Map reduce的云数据挖掘速度优化
加速比是在数据处理中运行消耗的时间的比率,K-means算法就是一种数据挖掘算法,加速比可以用来衡量次算法对于云数据挖掘速度优化条件。我们定义加速比,其中,sp为加速比,t1为单处理器下的运行时间,tp为p个处理器下并行计算的运行时间[16]。
分别测试数据集在1个节点和3, 5, 7, 9个节点的集群中k-means并行计算时间及其比率,得出加速比S1,S3,S5, S7,S9,结果如图5所示。随着云数据数据量的增加,其中的节点数也会随之增加,图5表明,同一数据集处理的加速比是逐渐增大的,也说明k-means算法在云数据挖掘中有更大的计算能力。
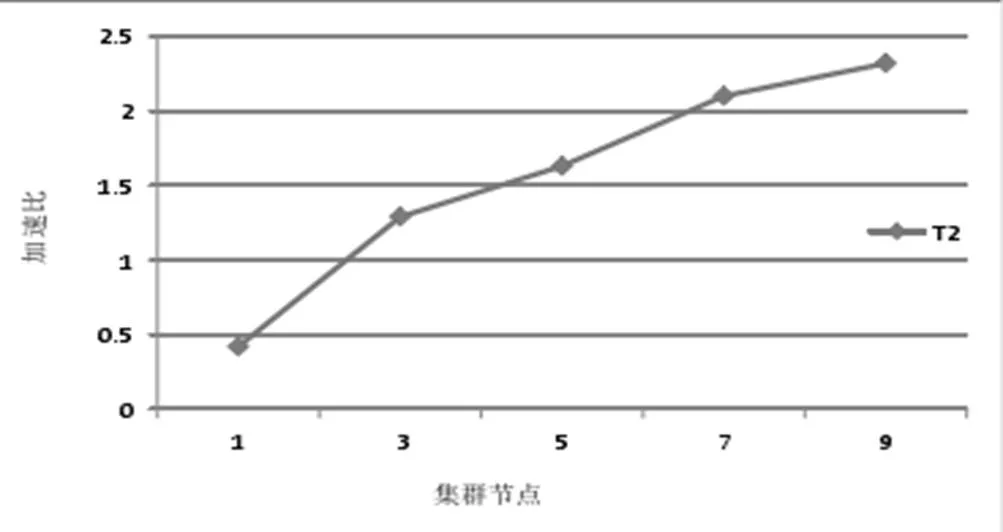
图5 K-means算法集群优化数据图
5 结束语
首先深入研究了K-means的关键算法在 Map Reduce 的核心设计思想和实现,并且根据Map Reduce中的聚类K-means算法对给定数据集进行试验。在掌握了 Map Reduce 并行计算框架这一基础之上,通过对多种数据挖掘算法进行分析,提出并构建一种基于Map Reduce 的数据挖掘算法并行化实现模型。根据此模型和次模型给定的数据结果,总结了K-means算法在Map Reduce中处理大规模数据时的性能瓶颈,并且做了性能试验分析。
当今时代网络的普及带来了海量数据难以处理的难题。研究的云数据中数据挖掘算法,是当今云数据迅速发展中一项较为复杂的技术,通过对K-means算法进行Map reduce化进行改进,从而能够更好地缩短云数据数据挖掘的时间,提高效率,最大限度发挥了的可用性、协同性、扩展性等特点。
[1]李国杰,程学旗.大数据研究:未来科技及经济社会发展的重大战略领域一一大数据的研究现状与科学思考[J].中国科学院院刊,2012.
[2]王佳隽,吕智慧,吴杰等.云计算技术发展分析及其应用探讨田.计算机工程与设计,2012.
[3]Apache Hadoop.[EB/OL]. http://hadoop.apache.org. (2013-12-01).
[4]李雪梅,张素琴.数据挖掘中聚类分析技术的应用[J].武汉大学学报(工学版),2009.
[5]田力.山东移动通信公司泰安分公司BI系统设计[D]. 山东大学,2009.
[6]张钊宁.数据密集型计算中任务调度模型的研究[D].国防科学技术大学,2011.
[7]从玉相.基于MapReduce的社区挖掘算法[D].上海交通大学,2013.
[8]Rakesh Agrawal,Ramakrishnan Srikant. Fast Algorithms for mining association rules in large databases. Very Large Data Bases,International Conference Proceedings,P487-499,1994.
[9]Shcn M, Tzcng U H,Liu D R. Multi-criteria task as-signment in workflow management term Sciences,2003. Proceedings of the 36th Annual Hawaii International Conference on.IEEE,2003.
[10]曹聪.云计算支持下的数据挖掘算法及其应用[D]. 广州大学, 2013.
[11]Yaakob SB, Kawata S. Workers placement in an in-dustrialenvironment[J].Fuzzy Setand Systems,1999.
[12]刘怡,张裁.基于负载平衡和经验值的工作流任务分配策略[J].计算机工程,2009.
[13]郭希娟,李墨华.基于多准则的动态任务分配算法[J]一计算机应用,2008.
[14]江小平,李成华,向文,张新访,颜海涛.k-means聚类算法的MapReduce并行化实现[[J].华中科技大学学报,2011.
[15]李贤虹.基于数据挖掘的读者个性化信息服务系统的研究与设计[D].南昌:南昌大学,2009.
[16]张立.多体系统传递矩阵法分布式并行计算研究[J]. 中国厂矿医学, 2009.

