SVD算法在MIMO系统模型降阶中的应用

闫哲+卢方明+周林

摘要：针对线性时不变高阶MIMO系统模型难以直接进行计算分析的问题，对高阶模型进行模型降阶。依据模型降阶理论，对线性时不变系统进行Lyapunov方程求解，得到线性系统的完全可控Gramians矩阵和完全可观Gramians矩阵，对Gramians矩阵进行Cholesky分解，得到Cholesky分解因子，分解因子通过SVD（singular value decomposition）法求得Hankel奇异值，从而确定系统的平衡变换阵。计算可控可观Gramians矩阵的左右特征空间基底矩阵，利用左右特征空间的基底矩阵求得原系统降阶的系统，通过Hankel SVD 方法确定降阶之后的误差范围。利用Matlab对SLICOT测试库中的便携式CDPlayer 120阶的高阶模型进行降阶，获取到50、30、20阶的降阶模型，对研究算法进行验证，结果表明，降阶效果理想。

关键词：线性时不变系统；模型降阶；Hankel奇异值

DOI：10.15938/j.jhust.2017.02.010

中图分类号： TP13

文献标志码： A

文章编号： 1007-2683（2017）02-0050-05

Abstract：For linear time invariant highorder system calculation and analysis model is difficult to directly， so we need to study on model order reduction of the model According to the basic theory of model order reduction， Lyapunov equation solution to linear time invariant system， completely controllable Gramians matrix and considerable Gramians matrix completely are obtained for a linear system， the completely controllable and considerable Gramians matrix Cholesky decomposition， the Cholesky decomposition factor and the factor decomposition by SVD （singular value decomposition） method for Hankel singular value are given to determine the balance of the system transformation matrix. The reduced order system is given by based matrix of left and right feature space which is obtained by the controllable and considerable Gramians matrix.The error bound for several reducedorder models are computed by using the method of Hankel SVD.In order to obtain the several reduceorder models，using Mtalb to turn CDPlyer highorder model that stored in SLICOT test library to a loworder system. The results show that the above order reduction method is feasible.

Keywords：linear time invariant system； model order reduction； balanced transformation

0引言

随着科学与技术的发展，很多大规模系统的模型结构越来越复杂，如高层建筑的结构受力分析，超大规模集成电路系統的仿真模型，电力系统网络的建模等[1]，由于对这些模型建立的方程组的规模极其庞大，计算难度及复杂度等问题逐渐突出，甚至有些实时计算无法实现[2-3]。因此，模型降阶成为了解决这一问题的重要方法。模型降阶就是将原大型系统的高阶模型用低阶模型来近似，并保持原系统的主要特性，如系统的稳定性及动态过程[4]。

目前模型降阶的主要方法有：①Krylov子空间类似方法，包括经典的Arnoldi和Lanczos降阶法[5]，该方法实际上就是模匹配的问题，单点不匹配情况下，可以进行多点匹配甚至是拟合的方法[6-7]；②正交分解模型降阶法，主要就是在时域中，将正交多项式作为基底进行空间上的展开，主要有Chebyshev多项式及Languerre多项式[8]；③平衡截断法，该方法应用广泛，对于中小模型降阶具有很大的优势[9-10]。

本文就是在经典平衡截断法的基础上，加入了SVD方法，对便携式CDPlayer模型进行降阶分析。通过对Lvapunov方程进行求解，获得平衡截断法的可控Gramians矩阵及可观Gramians矩阵，利用所得到可控可观阵进行SVD分解从而将120阶的系统降阶到50、30、20阶。利用此方法可以准确的得到降阶误差范围，并且可以保证系统降阶前后的稳定性及动态过程。

1模型降阶的基本理论

对系统模型进行降阶时，降阶模型必须满足以下几方面的性质：

1）输出的逼近误差要很小，最好能对某一个范数有一个全局误差界。

2）原系统既有的性质，例如稳定性和无缘性，降阶系统仍要保持这些性质。

3）给出的算法或者程序运行起来要简便有效[11-12]。

3SVD方法在CDPlayer模型中的应用

为了验证SVD降阶方法的降阶效果，引用SLICOT测试库提供的CDPlayer的模型作为验证标准。CD播放器的全阶模型描述了动态镜头致动器与摇臂之间的位置， 镜头位置的行为是由一组三阶的微分方程控制[16]。然而，当用于更新的便携式CDPlayer时，低阶系统就會难以实现。为了获得CDPlayer的高阶控制器，利用有限元近似的方式，获得的是两输入两输出的120阶模型，即n=120的模型。该模型的频率响应曲线如图1。

对CDPlayer播放器的高阶模型进行分析，得到该模型的特征值如图2（a）所示。图2（b）、（c）、（d）分别为降阶至50、30、20阶之后的特征值。从特征值分布图可以看出，在降阶至30阶以上时，基本可以保证原系统的性能，降阶到20阶后，保留了大部分原系统的性能。通过图2可以看出，该系统具有很高的实部和很低的虚部。

利用Matlab对CDPlayer模型求解Hankel 奇异值，得到奇异值大小分布如图3所示。

利用经验Gramian平衡降阶算法，计算该模型的平衡变换矩阵〖WTHX〗T，得到该系统的平衡系统，对平衡系统的经验Gramian矩阵进行奇异值分解。

通过上述分析可以确定，Hankel奇异值满足σ1≥σ2≥σ3…≥σn≥0，最后，利用Hankel奇异值大小，对模型进行Hankel奇异值求解，得到如图所示，可以知道Hankel的衰减速度非常快，因此可以确定该高阶模型可以近似到一个维数非常低的模型。

利用所求得Hankel奇异值可以求出模型降阶后的误差范围。处于作比较的目的，满阶之间的相对误差模型和降阶模型的计算如下[19]：

通过SVD平衡截断方法，得到CDPlayer降阶模型及误差范围见表1。

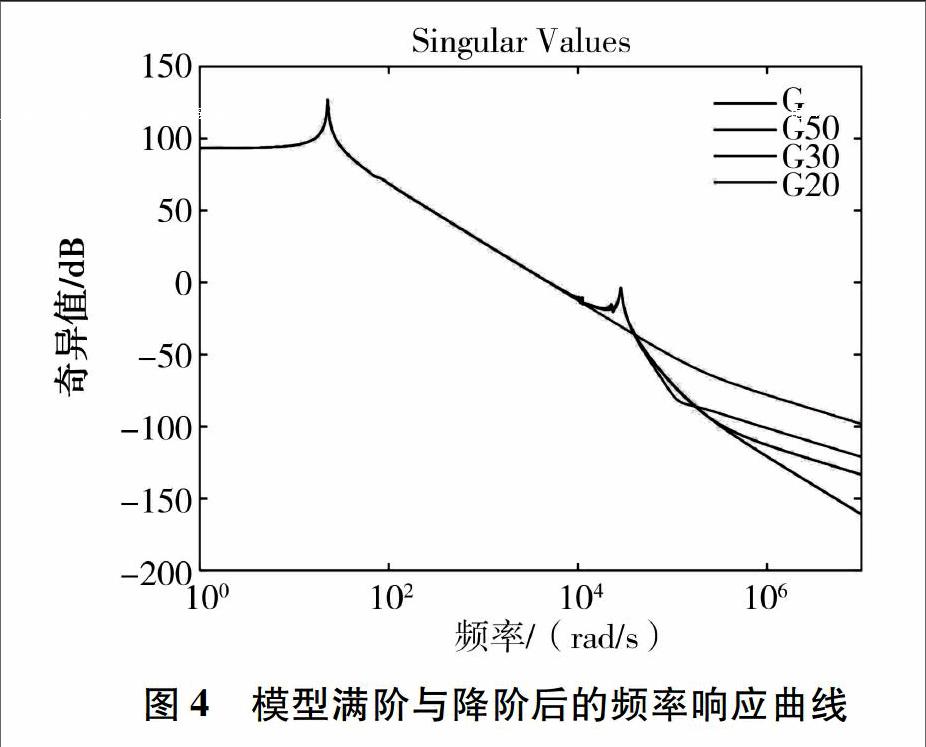
CDPlayer作为一个多输入多输出的模型，频率响应通常是由σi图表示，也就是说频率响应的最大奇异值来反应。模型满阶的频率响应曲线与降阶后的频率响应曲线如图4所示。

〖TP2B4.tif；S*2，BP〗〖TS（1〗〖HT5”H〗〖JZ〗

图4模型满阶与降阶后的频率响应曲线〖TS）〗

根据系统模型降阶可以降阶阶数判定条件∑tk=1σk/∑tk=1σk+1≥ε确定降阶的维数对模型分别降阶到50、30、20阶，每次降阶后的误差范围如图5所示。

从图4和图5可以看出，采用这种降阶方法可以将高阶模型降阶到一个良好的低阶形式。采用该方法对CDPlayer模型进行降阶，只要降阶阶数高于30，就可以与満阶的任意频率相匹配。当模型降阶到20阶时，在104～105范围之间遗失了一个共振峰。从奇异值的误差图可以得到一个确定的事实，那就是当降阶到30阶时，在所有频率内不匹配的误差很低。在进行模型降阶到20阶的情况下，除了共振峰丢失了之外，与原模型频率匹配误差也很低。

通过仿真得到的阶跃响应曲线对比，得知在30阶及以上的时候几乎保证了原模型的性能，降阶至20阶后，虽然降阶模型与原模型有一定的变化，但是可以保留大部分原系统的性能，所以可以判断降阶效果较为理想。模型降阶前后频率响应曲线如图6所示。

4结论

在平衡截断降阶方法的基础上，应用了SVD降阶方法，对模型进行Cholesky分解，求得能观能控的Gramians矩阵，根据Gramians矩阵利用求得Hankel奇异值对模型进行降阶处理，通过对CDPlaye模型进行了降阶实验，对这个2输入2输出的120阶模型进行降阶，分别降到50、30、20阶，通过仿真得到的阶跃响应曲线对比，得知在30阶及以上的时候几乎保证了原模型的性能。利用此方法可以明确的得出降阶之后的系统误差范围。总的来说，SVD降阶法对多输入多输出高阶模型的降阶处理是可行有效的。

参 考 文 献：

[1]DE Tuglie E， IANNONE S M， TORELLI F. A Coherency Recognition Based on Structural Decomposition Procedure[J]. Power Systems， IEEE Transactions on， 2008， 23（2）： 555-563.

[2]MARTINS N， SILVA F G， PELLANDA P C， et al. Utilizing Transfer Function Modal Equivalents of Loworder for the Design of Power Oscillation Damping Controllers in Large Power Systems[C]//IEEE PES General Meeting，2005： 2642-2648.

[3]SANCHEZGasca J J， CHOW J H. Computation of Power System Loworder Models from Time Domain Simulations Using a Hankel Matrix[J]. Power Systems， IEEE Transactions on， 1997， 12（4）： 1461-1467.

[4]OLIVIER P D. A Comparison of Reduced Order Model Techniques[C]//41st Southeastern Symposium on. IEEE， 2009： 240-243.

[5]朱耀麟， 杨志海， 陈西豪. 模型降阶方法研究[J]. 微计算机信息， 2011， 27（6）： 22-25.

[6]FREUND R W. Model Reduction Methods Based on Krylov Subspaces [J]. Acta Numerica， 2003（12）： 267-319.

[7]BAGLEY R L， CALICO R A. Fractional Order State Equations for the Control of Viscoelastically Damped Structures [J]. Journal of Guidance， Control， and Dynamics， 1991， 14（2）： 304-311.

[8]ANTOULAS A C. A New Result on Positive Real Interpolation and Model Reduction[J]. Systems Control Lett， 2005， 54： 361-374.

[9]熊纲， 杨超. 平衡截断方法在气动伺服弹性系统模型降阶中的应用[J]. 航空学报， 2001， 22（2）： 168-170.〖ZK）〗

[10]孟庆松， 原海勃. 模拟训练机模型简化算法的研究[J]. 电机与控制学报， 2012， 16（2）： 102-106.

[11]赵洪山， 宋国维， 江全元. 利用平衡理论进行电力系统模型降阶[J]. 电工技术学报， 2010， 25（2）： 127-133.

[12]李吉祥， 武俊峰， 樊丽颖. 离散系统降阶 H_

SymboleB@ 控制器的设计[J]. 电机与控制学报， 2011， 15（6）.78-83.

[13]WORTELBOER P M R， STEINBUCH M， BOSGRA O H. Iterative Model and Controller Reduction Using Closedloop Balancing， with Application to a Compact Disc Mechanism[J]. International Journal of Robust and Nonlinear Control， 1999， 9（3）： 123-142.

[14]ANTOULAS A， SORENSEN D， GALLIVAN K A， et al. Model Reduction and Realtime Control for Dynamic Data Driven Systems[J]. Dynamic Data Driven Simulation， 2005：56-89.

[15]胡明華， 胡寿松. 平衡降阶方法及其进展[J]. 南京航空航天大学学报， 1990（4）：14.

[16]孟庆松， 王海英. 高阶系统的奇异摄动模型的平衡降阶[J]. 哈尔滨理工大学学报， 2006， 11（3）： 82-84.

[17]GUGERCIN S， ANTOULAS A C. A Survey of Model Reduction by Balanced Truncation and Some New Results[J]. International Journal of Control， 2004， 77（8）： 748-766.

[18]盛洋， 赖旭芝， 吴敏. 基于模型降阶的平面三连杆欠驱动机械系统位置控制[J]. 自动化学报， 2014， 40（7）： 1303-1310.

[19]ANTOULAS A C， BEATTIE C A， GUGERCIN S. Interpolatory Model Reduction of Largescale Dynamical Systems[M]. Springer US Efficient Modeling and Control of LargeScale Systems， 2010： 3-58.

[20]REIS T， STYKEL T. A Survey on Model Reduction of Coupled Systems[M]. Springer Berlin Heidelberg： Model Order Reduction： Theory， Research Aspects and Applications， 2008： 133-155.（编辑：温泽宇）