牡丹花期不同预测方法初探及比较
王泳梅,马晓洁,范崇霞
牡丹花期不同预测方法初探及比较
王泳梅,马晓洁,范崇霞
(洛阳市王城公园,河南 洛阳 471000)
为能准确预测牡丹花期,更好地为牡丹文化节服务,对王城公园牡丹观赏区的早花牡丹品种‘朱砂垒’及春季开花植物的物候期、初花期的调查记录,利用SPSS19.0分析软件及Excel统计软件,分析牡丹的初花期与自身各物候期的相关性及与春花植物初花期的相关性,并对相关性显著的项目进行多元线性回归分析,建立牡丹花期预测数学模型,比较两个数学模型的准确性,结果表明‘朱砂垒’各物候期中的发芽期、立蕾期、风铃期与初花期的相关性极显著,建立预测数学模型为=58.649+0.1491+0.1422+0.2743;植物中樱桃、玉兰及早樱的初花期与‘朱砂垒’初花期相关性显著,建立牡丹花期预测数学模型为=-532.075+12.6931-4.7072+0.6213,依据以上两个数学模型可以初步对牡丹初花时间进行较准确的预测。
牡丹;物候期;花期预测;比较;相关性
1 牡丹花期预测的意义
洛阳牡丹雍容华贵,被誉为“国色天香”。自1983年以来,每年的牡丹文化节成为洛阳发展经济、招商引资和旅游品牌的形象代言。自1983年第1届牡丹花会开始,连续19届牡丹花会都是在4月15日至25日举行。2002年第20届牡丹花会时间首次提前至4月10日。2005年第23届牡丹花会,会期又提前至4月8日。2007年第25届牡丹花会再次把牡丹文化节赏花启动日固定至4月1日。可以说,历次会期的调整,都与牡丹花期息息相关。牡丹的自然花期受大气温度、光照及自身特性的影响在不同年份表现不一,为保证牡丹花会会期与花期的一致性,就必须提前做好花期的预测。为牡丹文化节的花情发布提供信息,也为牡丹花期控制提供依据。通过多年来的观测记载,结合影响牡丹花期的因素分析,总结推断出牡丹花期预测不同方法及其各自准确性比较,为牡丹花期的预测提供参考性依据。
2 影响牡丹花期的主要因素
影响牡丹花期分为内部因素和外部环境两方面。内部因素主要是牡丹自身的生理特性、遗传特性和激素水平等;外部环境包括温度、光照、水分和土壤条件等。
2.1 温度
牡丹生长周期存在的休眠以深度休眠为主。当气温等因素符合生长条件时,牡丹就能自动解除休眠,恢复生长。每年春季(1~4月份)随着平均气温的升高,牡丹会经过萌动、发芽、立蕾、展叶、园桃、平桃等阶段进入开花期,每个阶段持续的时间与本阶段气温高低有极大相关性,相对气温偏高,持续时间就短,相对气温偏低,持续时间就长。根据记载,在自然状态下,每年春季,当日平均温度稳定在3.6℃以上时牡丹花芽开始萌动、发芽; 6.5℃以上开始显蕾展叶,8.8℃以上花蕾迅速增大,16℃以上开始初花。牡丹每一发展时期对温度感受不同。所以,温度是花期预测的关键,温度是影响牡丹花芽解除休眠萌发生长的主要因素。
2.2 有效积温
每种植物都有其生长的下限温度。当温度高于下限温度时,才能生长发育。对植物生长发育起有效作用的高出的温度值,称作有效积温。牡丹从萌动到开花所经历的时间与有效积温密切相关。但目前还没有牡丹开花所需有效积温的准确值。据观察研究,牡丹不同发育阶段的生物学零度的值各不相同,牡丹开花的有效积温是在生物学零度以上温度之和。不同年份,随气候变化,达到牡丹开花所需有效积温的时间有所差异。从而出现了每年牡丹的初花时间不断变化。牡丹从萌动到开花的过程,实质上是由于外界温度不断升高从而刺激花芽发育的过程。所以,研究测算牡丹开花所需有效积温值对牡丹开花期的预测有非常重要的参考作用。
2.3 光照
在王雁的《北京市主要园林植物耐荫性及其应用的研究》论文中[1]提出“牡丹属于具有较高光补偿点,较低光饱和点的一类植物,对光能的有效辐射利用范围较窄,对生境光照状况要求较高”。在左丽娟的《光照强度对牡丹生长的影响》一文的研究中提出[2],光照对牡丹的花径大小、花量多少及花枝生长量都有一定的影响。不同的牡丹品种群由于遗传性和长期不同的栽培环境形成了各自特有的生态特性,其光照强度对它的影响作用也不一样。由于光照强度对牡丹生长发育的影响,进而影响牡丹的开花时间。因此,光照也是一个不可忽视的因素。
2.4 内源激素
植物内源激素是存在于植物体内调节植物萌发、生长、分化和发育等活动的生理活性物质,在植物体内其含量相对较低,常见的内源激素包含IAA,ABAGA,ZR和Eth。同大多数落叶植物一样,牡丹打破休眠后才能进行营养生殖生长。郑国升[3]在低温解除牡丹芽休眠进程中内源激素的变化一文中指出,GA3和ABA大小与低温累积期,休眠解除启动期、休眠基本解除期、休眠彻底解除期4个时期相对应,同时发现解除牡丹休眠是多种因素共同作用的结果,GA3等对休眠的解除起到积极的影响,而ABA对解除休眠具有一定的抑制作用。
2.5 自身长势
牡丹开花不仅需要N、P 、K 、Ca、 Mg 、S等大量元素,而且需要Fe、Mn、Cu 、Zn 等微量元素。在牡丹生长的年周期中,自春季芽萌动,贮存的养分迅速聚集在混合芽中,盛花时,混合芽中的养分已被用于开花和幼嫩营养器官的生长。因此,牡丹自身营养状况及生长势直接影响着牡丹的生长发育开花,同品种同株龄的牡丹营养充足,自身长势强的比长势弱的花期早。因此规范的生产管理对牡丹如期正常开花提供保障。新栽植牡丹因为根系恢复不健全往往会较正常植株提前开花。
3 材料与方法
3.1 试验地情况
试验地位于洛阳市王城公园牡丹观赏园,地处E112. 41°,N34. 67°,海拔150 m,年日照数为2 083 h,年平均气温14.7℃,年平均降水量达到560 mm,最热月为7月份,月平均气温为27.2℃;最冷月为1月,月平均气温为0.8℃;月平均气温年较差(最热月平均气温与最冷月平均气温的差值)为26.8℃;≥10℃日温的持续日数218 d;活动积温4 673℃。
3.2 试验材料
种植在洛阳牡丹观赏区的早花牡丹区,观测品种‘朱砂垒’,栽植密度1 m×1 m,观赏区为精细化管理。种植在王城公园内的春花植物:迎春、望春、连翘、樱桃、贴梗海棠、玉兰、早樱,精细化管理。
3.3 方法
3.3.1调查方法
随机在观赏区内选择30株10 a生以上的‘朱砂垒’牡丹,并对所选的牡丹做标记。多年对其物候期进行观测,根据各物候期的牡丹所表现的生物学特性及物候期记载的标准(见表1)。调查记录各年份牡丹的萌动期、发芽期、立蕾期、风铃期、园桃期、平桃期及初花期。

表1 牡丹物候期记载标准
注:物候期标准:试验对象达到各物候期程度所占比例。
随机在春花植物观赏区内选择春季开花植物,每个调查对象30株,调查记录各春花植物如:迎春、望春、连翘、樱桃、贴梗海棠、玉兰、早樱的初开期,初开的标准为5%进入初花阶段。
3.3.2统计方法
根据实际物候期记载时间进行物候期的天数转换:以1月1日为始日计算为1 d,1月2日为2 d,依此方法计算到各物候期的天数。例如:2000年‘朱砂垒’萌动时间为2月18日,用此方法转化计算出萌动期的天数为49 d。
统计分析方法:利用Excel软件统计数据,利用SPSS19.0 软件对所整理数据进行相关性分析,并对选定数据进行多元线性回归分析,并建立预测数学模型。
3.4 结果与分析
3.4.1物候期观测建模
通过掌握牡丹的生理特性,生物特性,综合考虑预测花期。根据牡丹年周期的生长特性,物候现象发生的顺序相关性规律,即顺序相关性规律体现在一年中,各物候期发生的顺序是一定的,并具有一定的相关性。前一物候期到来的早与迟和后续出现的物候期的早迟有密切的关系。根据前期发生的物候现象,对后期牡丹花芽的物候期进行预测。通过观察每个物候期花芽生长形态变化进行观察记录。萌动期牡丹麟芽膨大,麟片绽裂,继而开始发芽等其他后续物候生长进行历程。一般早开品种从麟芽萌动到开花大概需要65 d以上,晚开品种大概需要70 d以上。
研究搜集了洛阳王城公园2000-2008年期间‘朱砂垒’的物候期情况,对各物候期进行相关性分析:牡丹各物候期与牡丹初开期的相关性绝对值都在0.838以上,显著性小于0.05。其中发芽期与初开期相关性0.936,显著水平P=0.001,显著水平远小于0.01,说明发芽期对初开期影响极显著;立蕾期与初开期的相关性0.963,显著水平P=0.001,显著水平远小于0.01,说明立蕾期对初开期的影响极显著;风铃期相关性0.955,显著水平P=0.001,显著水平远小于0.01,说明风铃期对初开期的影响极显著。由表3可知,牡丹各物候期与牡丹初开期的相关性。
对与初开期(Y)影响极显著的发芽期(X1)、立蕾期(X2)及风铃期(X3)进行多元线性回归分析,建立基于发芽期、立蕾期及风铃期的多元方程对初开期的预测模型。由线性回归分析可知:模型的拟合度R2=0.971>0.95,拟合度效果非常好,且当F=45.222时,模型显著性水平P=0.002,远小于显著水平a=0.01,说明初开期与发芽期、立蕾期及风铃期具有显著的线性关系,由此可得初花期的预测数学模型:
=58.649+0.1491+0.1422+0.2743(1)
3.4.2同期春花植物物候期的对照比较
利用物候现象发生的相关性规律进行物候期预报,主要利用不同植物物候发生的顺序相关性,进行多年平行观测记录。通过多年观察与牡丹前后花期的其他春花植物,记录其在不同气候的各个年份表现的开花时间与同年牡丹花期的对比。例如:记录迎春、连翘、玉兰、早樱等植物的物候期,从而推断其与同一区域内牡丹花期前后关系,通过观察这些春花植物的物候期大致确定不同气候条件下牡丹的物候变化。
研究搜集了洛阳王城公园2009-2014年期间‘朱砂垒'的初开期及迎春、望春、连翘、樱桃、贴梗海棠、玉兰、早樱的初开期,把‘朱砂垒’及7种春花植物的初开期进行转换,以1月1日计算为1 d,1月2日为2 d,依此计算各物候期天数。
对研究对象初开期进行相关性分析[3],‘朱砂垒’初花期与樱桃初花期的相关性0.808,显著水平P=0.026、小于显著水平a=0.05,说明朱砂垒的初开期与樱桃花的初开期显著相关;玉兰的相关性0.750,显著水平P=0.043、小于显著水平a=0.05,说明‘朱砂垒’的初开期与玉兰花的初开期显著相关;早樱的相关性0.796,显著水平P=0.029、小于显著水平a=0.05,说明‘朱砂垒’的初开期与早樱的初开期显著相关。
对与‘朱砂垒’初开期(Y)相关性极显著的樱桃花初开期(X1)、玉兰花初开期(X2)及早樱花初开期(X3)进行多元线性回归分析[4],建立基于樱桃、玉兰及早樱三种植物花的初开期多元方程对朱砂垒初开期的预测模型。由线性回归分析可知:模型的拟合度R2=0.997>0.95,拟合度效果非常好,模型显著性水平P=0.004,远小于显著水平a=0.01,说明‘朱砂垒’的初花期与樱桃、玉兰及早樱的初花期具有显著的线性关系,由此可得初花期的预测数学模型:
=-532.075+12.6931-4.7072+0.6213(2)
3.4.3准确性分析
把2000-2008年的物候期数据回带入建立的预测数学模型(1)中,所得的预测日期与实际初花日期见表2。从表2中看到2000-2008年所预测的日期与实际初花期相差平均2 d。
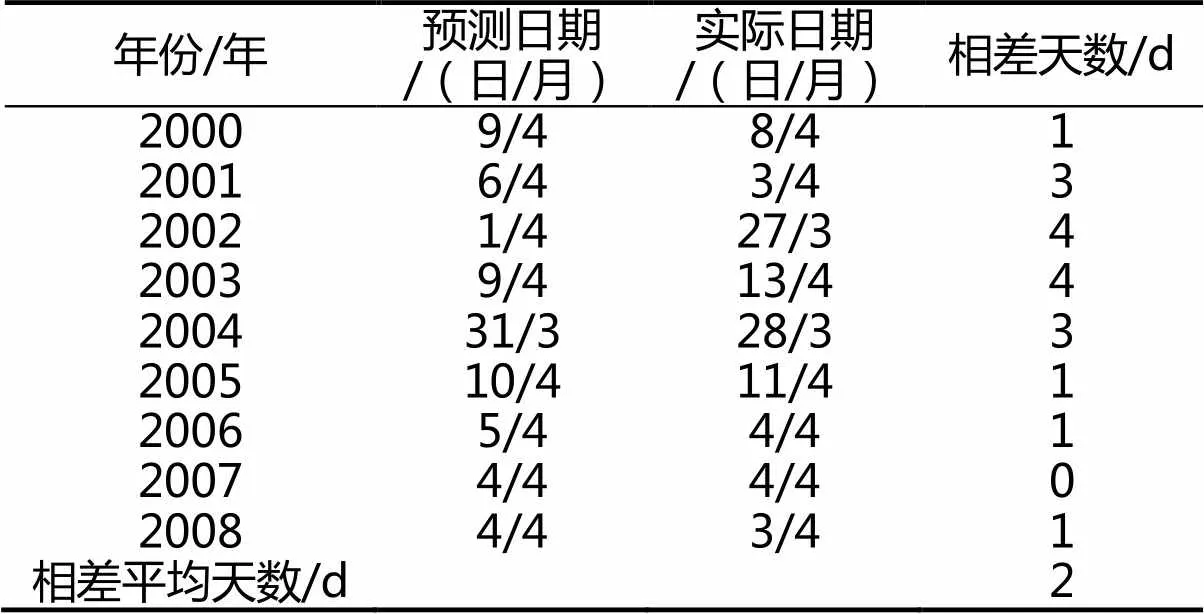
表2 实际花期与预测花期对照
把2009-2014年春花植物初花期的数据回带入预测数学模型(2)中,所得的预测日期与实际初花日期见表3。从表3中看到2009-2014年所预测的日期与实际初花期相差平均0.84 d。
把2009-2013年朱砂垒各物候期数据带入预测数学模型(1)中,所得的预测日期与实际初花日期见表4。从表4中看到2009-2013年初花预测日期与实际花期相差平均2.8 d。
把2015-2016年春花植物初花期的数据带入预测数学模型(2)中,所得的预测日期与实际初花日期见表5。从表5中看到2015-2016年所预测的日期与实际初花期相差平均2.5 d。

表3 实际花期与预测花期对照

表4 实际花期与预测花期对照

表5 实际花期与预测花期对照
4 结论
(1)‘朱砂垒’各物候期中的发芽期、立蕾期、风铃期与初花期的相关性极显著,以此为基础建立了花期预测模型(1):
=58.649+0.1491+0.1422+0.2743(1)
(2)7个春花植物中樱桃、玉兰、早樱的初花期与‘朱砂垒’初花期相关性显著,以此为基础建立了花期预测模型(2):
=-532.075+12.6931-4.7072+0.6213(2)
(3)利用模型(1)进行花期验证得出预测花期与实际花期相差平均2.8 d;利用模型(2)进行花期验证得出预测花期与实际花期相差平均2.5 d。
由此得出,在对牡丹初花期预测中,两种模型均有较高的准确度,可用于实际预测花期的操作。
[1] 王雁. 北京市主要园林植物耐荫性及其应用的研究[D]. 北京:北京林业大学,1996.
[2] 李嘉珏,张西方,赵孝庆,等. 中国牡丹[M]. 北京:中国大百科全书出版社,2011.
[3] 曲俊华,倪佳明. 多元回归模型分析与设计实现[J]. 中国电力教育,2007(1):140-142.
[4] 徐志敏,刘希玉. 多元回归分析及其在辅助决策中的应用[J]. 计算机工程,2004,30(21):129-131.
(责任编辑:王团荣)
The Peony Flowering of Different Prediction Methods Reviewed and Compared
WANG Yong-mei,MA Xiao-jie,FAN Chong-xia
(Luoyang Wang-Cheng Park, Luoyang Henan 471000, China)
(Purpose)To more accurately forecast the peony flowering period and better serve the Peony Cultural Festival.(Research)By tracking and accurately recording the phenological period for many years,combining the first bloom time of same period spring bloom plants,using SPSS19.0 analytical tool and Excel statistical tool,analyzing the relativity of the first bloom time of ‘Zhusha Lei' and its phenological period and the relativity of the first bloom time of ‘Zhusha Lei' and same period spring bloom plants,conducting multivariable linear regression analysis for the variables highly related with ‘Zhusha Lei' first bloomsome period,establishing a mathematical forecasting model,and comparing the accuracy of two mathematical models,(Result)the results indicate:the relativity of the budding time,Bud stage,Campanula period,and first bloom time of ‘Zhusha Lei'is highly notable,shown with mathematical forecasting model Y=58.649+0.149X1+0.142X2+0.274X3;the relativity of first blooming plants like cherry is highly notable,shown with mathematical forecasting model Y=-532.075+12.693X1-4.707X2+0.621X3,(Conclusion)hence we can make preliminary but relatively accurate forecast for the Peony first bloom time.
peony;phenological period; flowering period forecast; comparing; relativity
S 685.11
A
1003-2630(2017)01-0011-04
2017-02-20

