Runout of submarine landslide simulated with material point method*

Youkou Dong, Dong Wang, Mark F. Randolph

1. Centre for Offshore Foundation Systems, the University of Western Australia, Crawley, Australia,

E-mail: mark.randolph@uwa.edu.au

2. Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Ocean University of China, Qingdao 266100, China

Runout of submarine landslide simulated with material point method*

Youkou Dong1, Dong Wang2, Mark F. Randolph1

1. Centre for Offshore Foundation Systems, the University of Western Australia, Crawley, Australia,

E-mail: mark.randolph@uwa.edu.au

2. Shandong Provincial Key Laboratory of Marine Environment and Geological Engineering, Ocean University of China, Qingdao 266100, China

2017,29(3):438-444

Most of the present knowledge on submarine landslides relies upon back-analysis of post-failure deposits identified using geophysical techniques. In this paper, the runout of slides on rigid bases is explored using the material point method (MPM) with focus on the geotechnical aspects of the morphologies. In MPM, the sliding material and bases are discretised into a number of Lagrangian particles, and a background Eulerian mesh is employed to update the state of the particles. The morphologies of the slide can be reproduced by tracking the Lagrangian particles in the dynamic processes. A real case history of a submarine slide is back-analyzed with the MPM and also a depth-averaged method. Runout of the slides from steep slopes to moderate bases are reproduced. Then different combinations of soil and basal parameters are assumed to trigger runout mechanisms of elongation, block sliding and spreading. The runout distances predicted by the MPM match well with those from large deformation finite element analysis for the elongation and block sliding patterns. Horst and grabens are shaped in a spreading pattern. However, the current MPM simulations for materials with high sensitivities are relatively mesh sensitive.

Submarine landslide, runout, morphology, material point method, large deformation

Introduction

Submarine landslides are one of the most hazardous geological threats to subsea infrastructure, since they can transport vast volumes of sediments across continental slopes. Velocities of the slides can be up to 20 m/s, reaching final runout distances of hundreds of kilometers[1]. Most of the present knowledge on submarine slide relies upon back-analysis of post-failure deposits identified using geophysical techniques. Although various conceptual models have been proposed to analyze the runout mechanisms of slides, work on the runout process and evolution of morphologies remains limited. A variety of failure patterns have been reported: retrogressive failure in the Storegga slide generated a series of grabens and ridges[2], failure starting from the toe and progressing towards the head scarps was found together with compressional and extensional distortion[3], and out-runner blocks were observed in the Tampen slide[4]. In this paper, the runout of submarine slides is simulated using the materialpoint method (MPM). A real case history of a submarine slide is back-analysed with the MPM and also with a depth-averaged method (DAM). The runout morphologies predicted by the two methods are compared. Then different combinations of soil and seabed parameters are explored to trigger runout mechanisms of elongation, block sliding and spreading. The runout distances predicted by the MPM are compared with those from large deformation finite element (LDFE) analysis.

1. Methodology

The MPM, originating from the particle-in-cell method in computational fluid dynamics[5], can be regarded as a combination of finite element and meshfree methods. It possesses an inherent advantage for large deformation problems such as runout of landslides[6]and large-amplitude displacements of structural elements in soil[7], by means of discretising soil as Lagrangian particles. The material mechanical and kinematic properties (mass, volume, density, velocities, momentum, deformation gradients and stresses) are recorded and updated at the particles, and an Eulerianmesh is used for calculation in each incremental step only. Since the mesh is fixed in space, mesh entanglement such as occurs in conventional finite element methods is avoided. An in-house MPM program was developed, which stems from an open-source package Uintah[8]but was enhanced with a novel contact algorithm “Geo-contact”[9]and a GPU parallel computing strategy[10]. The updated Lagrangian calculation in explicit integration is based on the generalised interpolation material point method presented in Ref.[11].

The interaction between the slide and rigid base was considered with the “Geo-contact” by adjusting the nodal velocities of the slide. The slide and base might be in contact at specific nodes if both of their masses projected onto the nodes are non-zero. For a specific slide node in contact, the normal velocitynv was eliminated, and the tangential velocitytv was reduced by

where t is the maximum shear stress on the interface, A and m are respectively the area and mass represented by the node, tD is the time increment, determined through the Courant-Friedrichs-Lewy stability condition. In the following simulations, the tangential behaviour of the slide-base interface is regarded as: (1) No-slip: the slide is fixed at the interface with tlimited only by the strength of adjacent material. (2) Frictional: a maximum shear stress t, potentially lower than the strength of adjacent material, is specified along the interface.

Strain-softening and rate-dependency of the undrained shear strength of slides are expressed in multiplicative (Eq.(2)) or additive (Eq.(3)) form according to

where0us is the threshold shear strength,remd the strength ratio between the fully-remoulded and intact state (i.e., inverse of sensitivitytS), x the cumulative plastic shear strain with95x the plastic shear strain required to achieve 95% of remoulding, h the viscosity coefficient and n the shear-thinning index, y the shear strain rate and yrefthe reference shear strain rate. In Eq.(2), strain-softening is only imposed on the threshold shear strength of the soil but not the ratedependent portion[12]. This may be reasonable for a soil-fluid mixture, as strain-softening is considered for the soil and rate-dependency for the fluid. In contrast, the multiplicative expression in Eq.(3) implies that strain-softening is imposed on both the threshold shear strength and the rate-dependent portion. The two adjustments are therefore multiplicative in nature. This seems more appropriate for soil from a geotechnical perspective.

In all simulations with the MPM, a 4×4 particle configuration was allocated for each element fully occupied by particles prior to the calculation. The particle density was finer than the 2×2 particle configuration used in Refs.[9] and [10], to improve the numerical accuracy. The acceleration of gravity was g= 9.81m/s2. The Poisson’s ratio of the soils was taken as 0.49 to approximate constant volume under assumed undrained conditions. The Young’s modulus was taken as 100su0. The time step D t was determined by a Courant number of 0.3.

The DAM uses layer-integrated governing equations to describe the conservation of mass and momentum[13], simplifying 2-D runout into a 1-D problem. This simplification is acceptable for large scale events, where shallow water approximations to the Navier-Stokes equations are acceptable for overall behaviour of the runout. This approach is especially attractive on computational efficiency, requiring orders of magnitude less effort than other approaches. The volume of mass is discretized into a number of Lagrangian elements, which are solved, for example, using an explicit time-marching finite difference scheme. Each element advances at the local layer-averaged velocity. The thickness of each element is computed at the midpoint, but the volume remains constant.

The large deformation finite element (LDFE) approach used in the following study is the one termed“remeshing and interpolation technique by small strain (RITSS)” developed at the University of Western Australia[14,15]. The basic procedure is to divide the runout of the slides into hundreds or thousands incremental steps. The time step must be sufficiently small that all slide elements maintain acceptable shape during each step, then an updated Lagrangian calculation in the implicit integration scheme is performed. After that, the deformed slides are remeshed and the stresses and material properties at integration points and the nodal velocities and accelerations are mapped from the old mesh to the new mesh. The commercial finite element package, Abaqus, was used to conduct mesh generation and Lagrangian calculations.

2. Back-analysis of a real case

A real case history of submarine escarpment failure in the southern Mediterranean (The information ofthe real case was provided by Dr. Spinewine Benoit from Fugro GeoConsulting. The DAM simulations were performed by Dr. Spinewine Benoit together with Dr. Sam Ingarfield from Fugro AG Pty Ltd.) was back-analysed with the MPM and DAM with the idealized geometries shown in Fig.1(a). The failure was triggered by a steep slope at an inclination ofo13.75to the horizontal and the runout on a gently-inclined base reached a final distance of 420m: . The slidebase interface was assumed as no-slip. The soil parameters were obtained through laboratory tests of soil samples retrieved from the field. The submerged density of the slide was 525 kg/m3. The shear strength of the slide was approximated with Eq.(2), with su0= 15 kPa, drem=0.025(St=40), x95=45, viscosity coefficient h = 0.0167, shear-thinning index n=0.5 and reference strain rate yref=1s-1.

Fig.1(a) (Color online) Idealization of slide transect

Fig.1(b) (Color online) History of toe velocity and runout

In the MPM analysis, the element size was 0.2 m, i.e., : H0/60, which is sufficiently fine by trial calculations.0H represents the initial height of the slide. In total, there were 560 700 and 16 400 particles for the slide and base, respectively. The runout distances predicted by the DAM and MPM are close to the field observation (see Fig.1(b)). However, less mobility of the runout is predicted by the DAM than by the MPM: the peak velocities predicted by the DAM are approximately half those of the MPM predictions, the runout of the softening soil in the DAM analysis is delayed till 54 s, much later than the instant mobilisation in the MPM analysis. This is mainly attributed to the oversimplification of estimating the shear strain rate of the 1-D element in the DAM analysis, which is derived from the ratio of the velocity difference between the top and bottom nodes to the thickness of the element. This simplification implies that the velocity profiles are linear within the shear layer, which over-estimates the thickness of the shear layer.

Fig.2(a) (Color online) Evolution of runout morphologies

Fig.2(b) (Color online) Velocity contours by MPM at 25 s

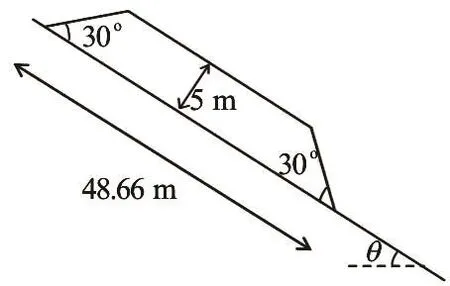
Fig.3 Problem definition for parametric study of runout behaviour (not to scale)

The runout morphologies predicted by the DAM and MPM analyses are similar, as shown in Fig.2. The failure is triggered at the front toe of the sliding mass and then retrogressively extends to the head. The runout from the steep slope is initially stacked in front of the steep slope and then elongates along the gentlyinclined base. Part of the original slide hangs on the slope as a relict due to the no-slip basal interface. Thethickness of the slide decreases with elongation in length, which causes a larger resistance along the basal interface.

Table 1 Configurations of submarine slide cases

3. Parametric studies

Four cases were designed to further study the runout morphologies (The LDFE simulation of runout mechanisms of elongation, block sliding and spreading were originally discussed in Ref.[16]) of planar submarine slides, based on an idealised geometry of original slides defined in Fig.3. The slide material was initially trapezoidal in shape with side-slopes of 30o, placed on a slope with an angle q to the horizontal. The height and length of the sliding mass were 5 m and 48.66 m, respectively. The runout behaviour depends on the combined influence of geometry and material properties of the slide, slope inclination and slide-base interaction. The parameters varied are listed in Table 1. For all analyses the submerged density of the sliding mass was r¢= 600kg/m3. The shear strength of the slide was approximated by Eq.(3). In the MPM analyses, the size of the square elements was selected as 0.1 m unless otherwise stated. In total, there were 307 200 slide particles and 6 000 base particles. Three flow mechanisms, elongation, block sliding and spreading, were observed through the cases in Table 1. Mesh dependency is detected in the spreading pattern due to strain-localisation for softening soil, while it is not observed in elongation and block sliding patterns for non-softening soils.

Fig.4 (Color online) Velocity contours predicted by MPM for Case 1 at 15 s

3.1 Elongation

Fig.5 (Color online) Influence of mesh size on runout distance for Case 1

Fig 6(a) (Color online) Evolution of runout morphologies for Case 1

Fig.6(b) (Color online) Evolution of runout morphologies for Case 2

The soils in Cases 1 and 2 have a constant shear strength of 2.5 kPa, i.e., rate-dependency and strainsoftening are ignored. The only difference between the two cases is the slide-base interface, which is frictional with a shear strength of 1 kPa for Case 1 and no-slip for Case 2. The sliding masses in Cases 1 and 2 move forward along the base, driven by the relative magnitudes of the self-weight and the friction on theinterface. The rear parts of the masses collapse since they are unstable. The sliding masses elongate and the thicknesses reduces, as shown in Fig.4 for Case 1. The frictional resistance along the slide-base interface thus increases due to the lengthened interface. The runout decelerates once the total friction on the interface exceeds the driving force due to the self-weight. The simulation of Case 1 was terminated before the runout had stopped, due to the heavy computational effort. The element size of 0.1 m in the MPM analysis is sufficiently fine to achieve convergence on the runout distances for Case 1, as shown in Fig.5. The runout in Case 2 stops at time :1 3s. As shown in Figs.6(a) and 6(b), evolutions of runout morphologies are similar between the LDFE and MPM analyses, therefore, similar final runout distances of :22s in Case 2 were predicted by the LDFE and the MPM analyses as shown in Fig.7.

Fig.7 (Color online) History of toe runout of Cases 1 and 2

Fig.8(a) (Color online) Evolution of runout morphologies

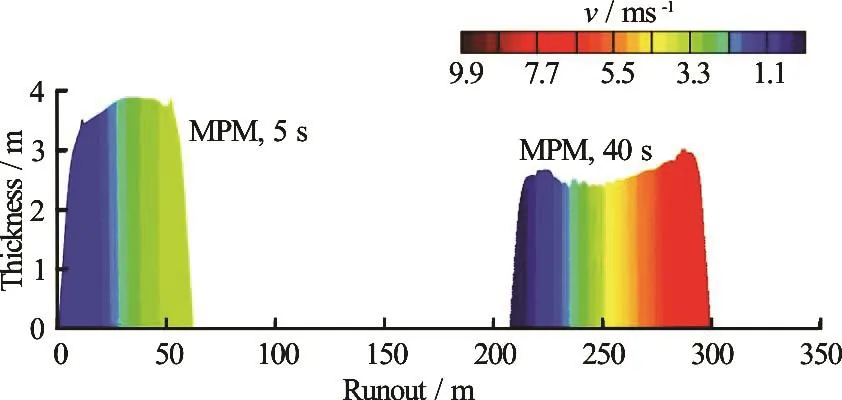
Fig.8 (b) (Color online) Velocity contour predicted by MPM

3.2 Block sliding

The soil in Case 3 was assumed as rate-dependent but strain-softening was not considered. In general the shear strength of the slide was increased by a factor of up to : 25 compared with the threshold shear strength. The height of the sliding mass reduces only slowly, so that the slide moves essentially as a block. The driving shear stress on the basal interface reduces from > 4.1kPa to : 2.1kPa, which is still larger than the maximum shear stress t on the interface. The slide continues to accelerate, achieving a toe velocity of 9.7 m/s at 40 s and a toe runout of :300m as shown in Fig.8(b) (but with the slide still moving when the computation was terminated). The element size of 0.1 m in the MPM analysis is sufficiently fine to achieve convergence on the runout distances, as shown in Fig.9. The runout morphologies and distances predicted by the LDFE and MPM analyses are similar, as shown in Fig.8(a). Velocity contours predicted by the MPM analysis are shown in Fig.8(b).

Fig.9 (Color online) History of toe runout of Case 3

3.3 Spreading with horsts and grabens

The soil in Case 4 was assumed as rate-independent, with intact shear strength of 5 kPa and a high sensitivity of 40 (essentially simulating softening by water entrainment as well as remolding). By contrast with the previous cases, the slope inclination was reduced to 2oin Case 4. Figure 10 shows the initialization and propagation of shear bands in the sliding mass. Soil collapses are initially triggered on both sides of the mass (at 2 s), followed by more failures spread progressively to the middle due to loss of lateral pressure (at 10 s). A series of horsts and grabens are formed with dislocation of the failed soil. The original horsts are inverted V-shaped wedges with two edges at an inclination of 45oto the base. The heavily disturbed soil is localized in the shear bands, while soil in the wedges is only slightly disturbed. The wedges tend to detach from each other due to velocity differences, as a result, the front wedges break away from the main body at 27 s (Fig.11(a)). The outrunner blocks are expected to reach a very long runout distance as reported in Ref.[17]. Therefore, the simulation was terminated at 27 s although the runout distance of 112 m was not finalised.

Fig.11(a) (Color online) Velocity contour at 27 s

Fig.11(b) (Color online) history of toe velocity and runout

At early stages the bottom soil is relatively intact with shear strengths larger than that on the slide-base interface of 1 kPa, therefore, the slide behaviour along the base is controlled by the latter. The velocity of the front toe accelerates to 3.2 m/s at 3.6 s, then decreases to 2.47 m/s at 10.5 s (see Fig.11(b)). However, after 10.5 s the runout of the front is controlled by the remoulded shear strength of the bottom soils of:0.125kPa , which is much lower than that on the slide-seabed interface. So the toe velocity increases again after 10.5 s, achieving 5 m/s at 21 s.

The propagation of shear bands in the sliding masses is mesh-sensitive due to the weak discontinuity bifurcation properties of constitutive models. Although several regularization mechanisms have been introduced, such as rate-dependent plasticity models, nonlocal models, gradient models and micro-polar continua models[18], this topic remains open. Greater mobility is seen for runouts with finer mesh as seen in Fig.11(b). As a result, the runout distances of the spreading pattern of submarine slides, especially with breakaway of out-runner blocks, cannot be predicted accurately.

4. Conclusion

Numerical simulation of the runout process of submarine slides with the MPM has been performed. A real case history of submarine slide was back-analysed with the MPM and DAM. Greater mobility of the runout was predicted by the MPM compared with the prediction by the DAM. The calculation of shear strain rates in the DAM analysis was considered as oversimplified. Different combinations of soil and seabed parameters were explored to trigger runout mechanisms of elongation, block sliding and spreading. The runout distances predicted by the MPM match well with those from LDFE analysis for the elongation and block sliding patterns. Horst and grabens are formed in the spreading pattern. However, the current MPM simulations for materials with high sensitivities are mesh sensitive.

Acknowledgements

The research presented here was supported by the Australian Research Council through an ARC Discovery grant (DP120102987). The work forms part of the activities of the Centre for Offshore Foundation Systems (COFS), currently supported as a node of the Australian Research Council Centre of Excellence for Geotechnical Science and Engineering and through the Fugro Chair in Geotechnics, the Lloyd’s Register Foundation Chair and Centre of Excellence in Offshore Foundations and the Shell EMI Chair in Offshore Engineering.

This work was also supported by resources provided by the Pawsey Supercomputing Centre with funding from the Australian Government and the Government of Western Australia and NVIDIA Corporation with the donation of the Tesla K40 GPU for the research.

[1] Jeong S. W., Leroueil S., Locat J. Applicability of power law for describing the rheology of soils of different originsand characteristics [J]. Canadian Geotechnical Journal, 2009, 46(9): 1011-1023.

[2] Kvalstad T. J., Andresen L., Forsberg C. et al. The Storegga slide: Evaluation of triggering sources and slide mechanics [J]. Marine and Petroleum Geology, 2005, 22(1-2): 245-256.

[3] Mountjoy J. J., McKean J., Barnes P. M. et al. Terrestrialstyle slow-moving earthflow kinematics in a submarine landslide complex [J]. Marine Geology, 2009, 267(3-4): 114-127.

[4] Solheim A., Berg K., Forsberg C. F. et al. The Storegga slide complex: repetitive large scale sliding with similar cause and development [J]. Marine and Petroleum Geology, 2005, 22(1-2): 97-107.

[5] Harlow F. H. The particle-in-cell computing method for fluid dynamics [J]. Methods in Computational Physics, 1964, 3: 319-343.

[6] Andersen S., Andersen L. Modelling of landslides with the material-point method [J]. Computational Geosciences, 2010, 14(1): 137-147.

[7] Phuong N. T. V., Van Tol A. F., Elkadi A. S. K. et al. Numerical investigation of pile installation effects in sand using material point method [J]. Computational Geosciences, 2016, 73: 58-71.

[8] Guilkey J., Harman T., Luitjens J. et al. Uintah code (Version 1.5.0), Computer program (2010) [EB/OL]. Available at .

[9] Ma J., Wang D., Randolph M. F. A new contact algorithm in the material point method for geotechnical simulations [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(11): 1197-1210.

[10] Dong Y., Wang D., Randolph M. F. A GPU parallel computing strategy for the material point method [J]. Computers and Geotechnics, 2015, 66: 31-38.

[11] Bardenhagen S. G., Kober E. M. The generalized interpolation material point method [J]. Computer Model Engineering and Science, 2004, 5(6): 477-495.

[12] Boukpeti N., White D. J., Randolph M. F. et al. Strength of fine-grained soils at the solid-fluid transition [J]. Géotechnique, 2012, 62(3): 213-226.

[13] Imran J., Harff P., Parker G. A numerical model of submarine debris flow with graphical user interface [J]. Computers and Geosciences, 2001, 27(6): 717-729.

[14] Hu Y., Randolph M. F. A practical numerical approach for large deformation problems in soil [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2015, 22(5): 327-350.

[15] Wang D., White D., Randolph M. F. Large-deformation finite element analysis of pipe penetration and large amplitude lateral displacement [J]. Canadian Geotechnical Journal, 2010, 47(8): 842-856.

[16] Wang D., Randolph M. F., White D. J. A parametric study of submarine debris flows using large deformation finite element analysis [R]. The VI Report for the JIP Project Modelling of Submarine Slides and Their Impact on Pipelines from Minerals and Energy Research Institute of Western Australia, Project No. M395, 2011.

[17] Ilstad T., De Blasio F. V., Elverhøi A. et al. On the frontal dynamics and morphology of submarine debris flows [J]. Marine Geology, 2004, 213(1-4): 481-497.

[18] Li S., Hao W., Liu W. K. Mesh-free simulations of shear banding in large deformation [J]. International Journal of solids and structures, 2000, 37(48-50): 7185-7206.

10.1016/S1001-6058(16)60754-0

February 19, 2017, Revised March 15, 2017)

*Biography:Youkou Dong, Male, Ph. D.