三维人体运动跟踪中形状特征表述重建*

周 斌， 马 玲

(石河子大学 体育学院， 新疆 石河子 832003)

三维人体运动跟踪中形状特征表述重建*

周 斌， 马 玲

(石河子大学 体育学院， 新疆 石河子 832003)

针对在重建三维人体运动跟踪形状特征时，人体运动姿态重建结果与真实值具有较大偏差且不能长时间有效跟踪的问题，提出基于联合优化法的三维人体运动跟踪形状特征表述重建方法.采用POCS算法将三维人体运动跟踪中的形状捕捉问题转换为正则规划问题，实现对三维人体运动跟踪中的形状捕捉.采用Bayes理论统计估计方法，将捕捉到的形状数学建模问题转化为目标函数最大化问题.采用Fisher线性判别分析法对三维人体运动跟踪中的形状特征点进行自动定位，利用联合优化法重建已经定位的形状特征表述.结果表明，所提方法可以有效捕捉三维人体运动跟踪中的形状特征，且重建精度较高，准确性较好.

三维人体； 运动跟踪； 形状特征； 表述； 重建； 捕捉； 定位； POCS算法

近年来，人体运动的跟踪与分析成为了图像处理与计算机视觉领域中备受关注的研究热点.可以利用单个或多个摄像机从包含人体运动的图像序列或视频中检测、识别、跟踪人体，并对其进行理解和描述，且该方面的研究属于图像分析领域[1-3].在对人体运动进行跟踪时，多采用三维方式进行分析.从技术角度而言，对三维人体运动跟踪进行分析的研究内容相当丰富，主要涉及模式识别、图像处理、计算机视觉、人工智能及形状特征表述分析等方面[4-6]，其中，形状特征表述是该领域亟待解决的问题，受到广大学者的重视，也出现了很多较好的研究方法.文献[7]提出基于局部特征的形状特征描述重建方法，该方法以大规模图像集为数据源，进行较为精确的重建工作，使重建后的形状特征描述与原始形状特征描述相似.文献[7]对目前的形状特征进行概述，采用局部特征及匹配特征块方法，实现对形状特征描述的重建，但该方法存在重建精度较低的问题；文献[8]提出基于数据驱动的形状特征表述重建方法，该方法充分利用大量数据训练得到形状特征信息，估计其信噪比，检测并标记噪声污染严重的特征，得到鲁棒性较好的形状特征表述参数，从而实现采用数据驱动方法对形状特征表述进行重建的目的，但是该方法同样存在重建精度较低的问题；文献[9]提出基于亚高斯随机投影的形状特征表述重建方法，该方法首先给出两种新型的测量矩阵(稀疏投影矩阵和非常稀疏投影矩阵)，利用亚高斯分布的有界性证明两种矩阵存在的必要性，同时，利用两种矩阵的稀疏性简化重建过程，实现形状特征表述重建，但该方法存在重建过程耗时过长的问题.

针对上述问题，本文提出基于联合优化法的三维人体运动跟踪中的形状特征表述重建方法，并进行了相关的实验分析.结果发现采用该改进方法时，其重建精度和效率均优于传统重建方法.

1 形状特征分析

1.1 形状特征的捕捉

在三维人体运动跟踪中进行形状捕捉实际上就是对三维图像序列中的运动模型进行检测、跟踪并记录相应的运动形状轨迹信息.采用多个摄像机以各种视觉角度对背景连续采集三维人体运动跟踪图像，并建立一个初始背景统计模型[10-11].对背景中像素点的颜色均值和方差进行计算，其计算公式分别为

(1)

(2)

式中：Bi为每个像素点的颜色矩阵；K为图像数量.

采用背景减除法提取三维人体运动跟踪图像的形状目标值，其表达式为

(3)

式中：Q(x，y)为图像前景灰度值；B(x，y)为图像背景灰度值；L为阈值.

当采用简单背景减除法提取形状目标时，在检测结果中发现含有大量噪声干扰.为了正确捕捉三维人体运动跟踪中的形状特征，采用基于修正边缘的背景减除法去除噪声，此时形状目标值的相应表达式为

(4)

式中：t0为噪声周期；t(x)为噪声所在频段；A为图像背景尺度信息.

假设已知Z是由三维人体运动跟踪图像样本集训练得到的一个数据集合，则图像在数据集合Z下的稀疏表示定义式为

E(x，y)=αZ

(5)

式中，α为稀疏表示系数.

采用POCS算法将三维人体运动跟踪中的形状捕捉问题转换为正则规划问题进行求解，则正则规划函数可以表示为

(6)

实现三维人体运动跟踪中的形状捕捉后得到优化目标函数，其表达式为

(7)

式中：gr为r时刻采集的图像梯度值；Dr为r时刻的投影算子；Hr为r时刻的采集速度；Mr为r时刻采集图像的质量；f为像素总数；λ为图像采集系数；γ为采样矩阵.

1.2 形状特征数学模型的构建

在对三维人体运动跟踪中的形状特征进行捕捉的基础上，采用Bayes理论统计估计方法对三维人体运动跟踪中形状特征的数学模型进行构建.图1为人体骨架模型，该模型共有25个自由度，各个子节点坐标系与父节点坐标系之间的关系可以表示为

I=T(tx，ty，tz)RxRyRz

(8)

式中：I为父节点坐标；Rx、Ry和Rz分别为x、y和z轴方向的子节点坐标；T(tx，ty，tz)为根节点到坐标系原点的位移.

图1 人体骨架模型

图1中Q0～Q9为人体骨架中不同身体结构的坐标点；q1～q30为不同三维坐标点；TRHR、TRKH和TRFA分别表示右臀部到根节点的初始平移，右膝盖到右臀节点的初始平移和右脚部到右踝部的初始平移.

采用Bayes理论统计估计方法将对三维人体运动跟踪中形状特征数学模型的构建问题转化为图像估计问题，即目标函数最大化问题.根据Bayes理论统计估计方法得到的条件概率表达式为

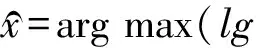
(9)

式中，P(·)为图像概率密度函数.

三维人体运动跟踪中形状特征的数学模型表达式为

d(x，y))+Vk[x，y]

(10)

2 形状特征表述重建方法的改进

2.1 形状特征点的自动定位

在建立三维人体运动跟踪形状特征数学模型的基础上，采用Fisher线性判别分析法对三维人体运动跟踪中的形状特征点进行自动定位.假设三维人体运动跟踪中形状特征邻域为某一矩阵，则对应的卷积函数可以表示为

(11)

采用Fourier变换法对三维人体运动跟踪中的形状特征噪音进行消除，从而减少高频分量.假设图像函数经过Fourier变换后可表示为F(x，y)，且H(x，y)为低通滤波的转移函数，G(x，y)为经过低通滤波后图像的Fourier频谱函数，则

G(x，y)=H(x，y)F(x，y)

(12)

(13)

此外，不同样本的类内离散度矩阵Si和总类内离散度矩阵S可以分别表示为

(14)

S=S1+S2

(15)

(16)

经过投影后同类形状特征应该尽可能聚集，而不同类形状特征应该尽可能分开，从而使得类内离散度变小，而类间离散度变大.Fisher线性判别准则可以表示为

(17)

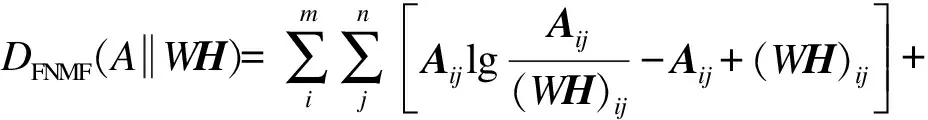
QSe-QSc

(18)

式中：Q为大于0的常数；W为权值系数；Aij为图像背景尺度的特征向量；Se为权值矩阵H的类内差距；Sc为权值矩阵H的类间差距.

2.2 改进重建方法的实现

(19)

式中：F(Θ)为基本矩阵函数；R(q)为q波段下相机参数向量；T为时间向量.

修正后的坐标最小化目标函数可以表示为

(20)

式中，ρ为图像特征点密度.

假设变化所需样本的最小数量为Nh，为了获取准确的形状特征表述，需要至少进行Ns次迭代，则最终三维人体运动跟踪中图像轮廓特征变量可以表示为

(21)

式中：ξ为特征外点率；p为常数.

为了防止在重建过程中产生高斯噪声，利用硬阈值法对形状特征表述进行降噪处理，即

θ(b+1)=ψΔx(b+1)

(22)

(23)

式中：θ(b+1)(n)为差别阈值θ(b+1)的第n个元素；ψ为小波稀疏基；Δx(b+1)为绝对阈值；η(b+1)为门限值.

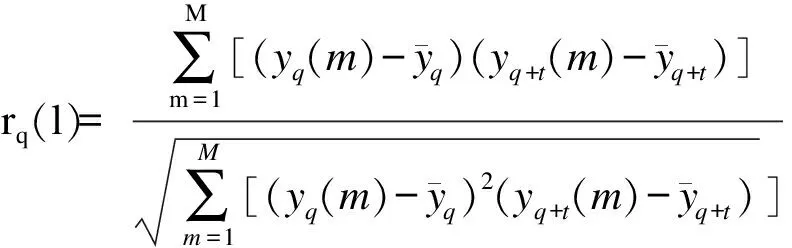
(24)

综上所述，在对三维人体运动跟踪形状特征点进行自动定位的基础上，可以采用联合优化法对三维人体运动跟踪中的形状特征表述进行重建，但需要进行实验对比分析.

3 结果与分析

3.1 实验参数设置

为了验证改进形状特征表述重建方法在三维人体运动跟踪中的有效性及可行性，需要进行实验对比分析.实验设备包括6个校准相机和两个采集卡.实验采样率为30帧/s，采样图像像素分辨率为320×240.在Matlab2010环境下(并未进行代码优化和并行处理)，采用背景减法提取人体轮廓.运动者的运动空间为2m×2m×2m，将该空间划分成尺寸为2cm×2cm×2cm的子空间.采用改进方法得到三维运动跟踪中的形状特征，初始化时间为120ms.实验中约3/5的时间消耗在特征表述重建上，剩余时间用于特征处理及特征表述的获取.Michoud硬件系统选用4个标定相机，且由一台计算机控制.

3.2 实验结果

3.2.1 不同方法下的相关性对比

采用稀疏随机投影法[9]、基于局部特征重建法(代数法)[7]与改进重建法进行对比分析，结果如图2所示.

图2 不同方法下的相关性对比

在三维人体运动跟踪中可以根据追踪动态时间下的振动情况判定跟踪人体运动情况，若出现较大波动，则表明运动幅度较大.将不同方法的测试结果与原数据进行对比，若振型相同，则表示方法准确，此时与具体振动幅度无关.由图2可见，当采用稀疏随机投影法、基于局部特征重建法与改进重建法进行分析时，在0～100 s范围内利用不同方法获得的振动情况均不低于三维人体运动跟踪原数据，但在100～220 s时间段内，利用不同方法获得的振动情况差别较为明显.观察图2可知，采用改进重建法进行采样时并未破坏图像谱间的相关性结构，改进重建法观测向量的谱间相关性与三维人体运动跟踪图像保持了良好的一致性，这与理论推导出的结果相一致.当利用改进重建法进行重建时，能够充分利用三维人体运动跟踪数据具有的较强谱间相关性特点，将数据整合到重建模型中，因而可以增加重建性能，可见改进重建法具有一定的优势.

3.2.2 不同方法的相关收敛性对比

为了验证本文所提方法的收敛性，在人体运动过程中抓拍某一特性动作作为待处理的原始图像，具体图像如图3所示.

图3 原始图像

利用本文所提改进重建法、基于局部特征重建法和稀疏随机投影法进行三维人体形状特征重建.通过测试不同方法重建目标后的三维像素点，描绘不同图像测定结果的三维重建图像，实现性能对比分析.不同方法下的形状特征表述重建对比如图4所示，其中Lx、Ly、Lz分别代表不同方向的像素值.由图4可见，稀疏随机投影法和基于局部特征重建法出现了手臂动作形状重建表述错误或是手臂高抬角度错误的问题.当采用改进重建法时，该方法对手臂前后顺序、高抬角度和手臂动作等形状特征的表述均较为准确，精度较高，因而具有一定的优势.

4 结 论

针对传统方法对三维人体运动跟踪中的形状特征进行重建时精度较低的问题，本文在对形状特征点进行自动定位的基础上，提出基于联合优化法的形状特征表述重建方法，并进行了相关实验分析.结果表明，所提出的改进重建法相比传统方法具有更高的准确性，且重建精度较高.

图4 不同方法下的形状特征表述重建对比

[1]李敏，宋曰聪，吴斌，等.基于Beowulf机群中改进粒子滤波的3D人体运动跟踪 [J].计算机工程与应用，2015，51(14)：17-22.

(LI Min，SONG Yue-cong，WU Bin，et al.Three-dimension human motion tracking based improved particle filter on Beowulf cluster system [J].Computer Engineering and Applications，2015，51(14)：17-22.)

[2]赵军，於俊，汪增福.基于改进逆向运动学的人体运动跟踪 [J].智能系统学报，2015，24(4)：548-554.

(ZHAO Jun，YU Jun，WANG Zeng-fu.Human motion tracking based on an improved inverse kinematics [J].CAAI Transactions on Intelligent Systems，2015，24(4)：548-554.)

[3]杨凯，魏本征，任晓强，等.基于深度图像的人体运动姿态跟踪和识别算法 [J].数据采集与处理，2015，30(5)：1043-1053.

(YANG Kai，WEI Ben-zheng，REN Xiao-qiang，et al.Depth image based human motion tracking and recognition algorithm [J].Journal of Data Acquisition & Processing，2015，30(5)：1043-1053.)

[4]张殿勇，苗振江.基于模型的无标识人体运动捕捉研究 [J].北京交通大学学报，2014，38(2)：42-49.

(ZHANG Dian-yong，MIAO Zhen-jiang.Research on model-based markerless human motion capture [J].Journal of Beijing Jiaotong University，2014，38(2)：42-49.)

[5]陈曦，孟庆虎.骨架关节点跟踪的人体行为识别方法 [J].河南科技大学学报，2015，26(2)：43-48.

(CHEN Xi，MENG Qing-hu.Human behavior recognition method for skeleton joint point tracking [J].Journal of Henan University of Science & Technology，2015，26(2)：43-48.)

[6]李平，魏仲慧，何昕，等.采用多形状特征融合的多视点目标识别 [J].光学精密工程，2014，22(12)：3368-3376.

(LI Ping，WEI Zhong-hui，HE Xin，et al.Object recognition based on shape feature fusion under multi-views [J].Optics and Precision Engineering，2014，22(12)：3368-3376.)

[7]冯霞，秦昆，崔卫红，等.高分辨率遥感影像目标形状特征多尺度描述与识别 [J].遥感学报，2014，18(1)：90-104.

(FENG Xia，QIN Kun，CUI Wei-hong，et al.Multiscale description and recognition of target shape in high-resolution remote sensing images [J].Journal of Remote Sensing，2014，18(1)：90-104.)

[8]刘璇，李海生，蔡强，等.三维形状特征提取技术研究进展 [J].计算机科学与探索，2014，8(5)：513-524.

(LIU Xuan，LI Hai-sheng，CAI Qiang，et al.Review of 3D shapes feature extraction [J].Journal of Frontiers of Computer Science and Technology，2014，8(5)：513-524.)

[9]崔宝侠，田佳，段勇，等.基于图论分割的肺部CT图像的三维重建 [J].沈阳工业大学学报，2015，37(6)：667-672.

(CUI Bao-xia，TIAN Jia，DUAN Yong，et al.Three-dimensional reconstruction of lung CT images based on graph theory segmentaion [J].Journal of Shenyang University of Technology，2015，37(6)：667-672.)

[10]朱延娟，倪周松.基于离散点曲率的细胞图像形状特征表述 [J].计算机应用，2015(增刊2)：267-270.

(ZHU Yan-juan，NI Zhou-song.Description of shape feature for cell image based curvature of discrete points [J].Journal of Computer Applications，2015(Sup2)：267-270.)

[11]郭鹏宇，苏昂，张红良，等.结合纹理和形状特征的在线混合随机朴素贝叶斯视觉跟踪器 [J].光学学报，2015，31(3)：195-205.

(GUO Peng-yu，SU Ang，ZHANG Hong-liang，et al.Online mixture of random Naive Bayes tracker com-bined texture with shape feature [J].Acta Optica Sinica，2015，31(3)：195-205.)

(责任编辑：尹淑英 英文审校：尹淑英)

Reconstruction for shape feature representation in 3D human motion tracking

ZHOU Bin, MA Ling

(College of Physical Education, Shihezi University, Shihezi 832003, China)

Aiming at the problem that during the reconstruction of shape feature in the 3D human body motion tracking, the reconstruction results of human motion postures compared with the real values have a large deviation and the effective tracking for a long term can not be realized, a reconstruction method for shape feature representation in 3D human body motion tracking based on the combined optimization method was proposed. The shape capture problem in 3D human body motion tracking was transformed into the regular programming problem with the POCS algorithm, and thus the shape capture problem in 3D human body motion tracking could be realized. The statistical estimation method of Bayes theory was adopted, and the captured shape mathematical modeling problem was transformed into the objective function maximization problem. With the Fisher linear discriminate analysis method, the shape feature points in 3D human body motion tracking were automatically located, and the located shape feature representation was reconstructed with the combined optimization method. The results show that the proposed method can effectively capture the shape feature in 3D human body motion tracking, and has high reconstruction precision and good accuracy.

3D human body; motion tracking; shape feature; representation; reconstruction; capture; localization; POCS algorithm

2016-11-12.

“十二五”规划重点课题资助项目(01020433-XJ1512).

周 斌(1981-)，男，甘肃兰州人，讲师，硕士，主要从事运动训练与人体工程学等方面的研究.

10.7688/j.issn.1000-1646.2017.03.18

TP 391.4

A

1000-1646(2017)03-0340-06

*本文已于2017-05-08 20∶25在中国知网优先数字出版. 网络出版地址： http：∥www.cnki.net/kcms/detail/21.1189.T.20170508.2025.018.html