一种设计Helmholtz线圈的快速优化方法

林 哲， 邹 军

(清华大学 电机工程与应用电子技术系， 北京 100084)

一种设计Helmholtz线圈的快速优化方法

林 哲， 邹 军

(清华大学 电机工程与应用电子技术系， 北京 100084)

本文讨论利用Helmholtz线圈结构产生匀强磁场时的线圈参数设计问题。该问题以不均压系数作为指标衡量一个区域磁场的均匀程度，旨在通过参数设计使目标区域磁场最均匀化。在解决这个实际应用背景下的多参数优化问题的过程中，本文通过线圈参数的预估、合理磁感应强度计算方法及优化算法的选取，大幅缩减求解过程中的计算量，提出了基于Matlab的一种更加高效快速的Helmholtz线圈设计方法。

Helmoltz线圈；匀强磁场；参数优化

0 引言

如果有一对相同的载流圆线圈彼此平行且共轴，通以同方向电流，当线圈间距等于线圈半径时，两个载流线圈的总磁场在轴的中点附近的较大范围内是均匀的，这样的一组线圈称为Helmholtz线圈。由于其产生轴向均匀磁场的特点，Helmholtz线圈在生产和科研中有较大的实用价值，常用来产生实验室或工业所需的一定区域内的匀强磁场。

关于Helmholtz线圈产生磁场的研究已持续多年。由于单组Helmholtz线圈产生的磁场均匀程度尚不理想，通常采用多组Helmholtz线圈结构产生均匀性较好的匀强磁场。前人的相关研究中已对载流圆线圈组产生均匀磁场的原理进行了详细的分析，并提出产生磁场的几种实用圆线圈组合，如麦克斯韦四线圈、布朗贝克四线圈等。

本文讨论的是利用两对Helmholtz线圈结构产生匀强磁场时的参数设计问题，定义“不均压系数”作为定量衡量区域磁场均匀程度的指标，旨在通过参数设计使目标区域磁场最均匀化。该问题是一个实际应用背景下的多参数优化问题，如果直接求解，存在计算量过大的困难。针对求解过程中的这一难点，本文提出了一种更加高效快速的方法，创新性地通过预估参数范围、选取合理磁场计算方法及优化算法可大幅缩减求解过程中的计算量，最终快速地设计出Helmholtz线圈的最优参数并检验设计结果的合理性与计算量缩减的事实性。

1 问题描述及分析

1.1 问题描述

为了获得一定区域上的匀强磁场，通常采用多组Helmholtz线圈结构。考虑这样一种具体的情境：一种两对线圈的结构如图1所示，其中线圈半径a1，a2，线圈间距h1，h2，以及线圈中通过电流i1，i2均为可变化量。

为了定量衡量关注区域(线圈组1的两线圈之间区域)的磁场均压程度，过轴线做截面ABO2O3，取CD=0.8×AB和EO3=0.8×AO3，并在CD和EO3线段上每边均匀取20采样点，从而形成如图2所示的采样点，定义z方向B的不均压系数为

(1)

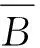
问题如下：如果规定a1=a2=0.5 m，i1=1 A，问β1、β2、i2如何取值可以使得δ最小，即关注区域磁场“最均匀”。

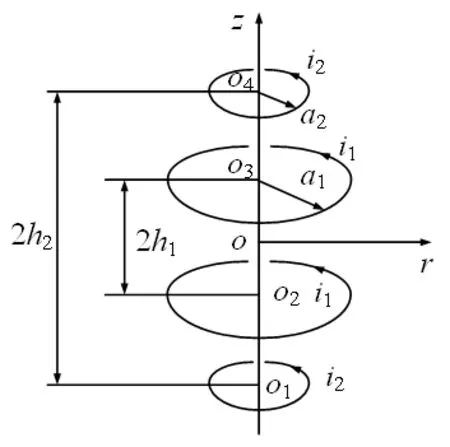
图1 线圈结构示意图

1.2 问题分析

该问题的目标是通过参数设计，利用Helmholtz线圈结构模型获得一定区域中z方向上的匀强磁场。为了衡量获得的匀强磁场质量，给出采样区域的“磁场不均压系数δ”作为指标，其数值越小表示所获得的匀强磁场质量越佳。本题给定的求解约束有两组线圈的半径a1与a2、线圈组1中通过的电流i1，因此问题的本质是一个含约束的多参数优化问题。在本题的参数设计过程中，直接求解时由于计算量过大所导致的求解时间过长是一个设计难点。其计算量主要来自于三个方面：求解区域过广，即参数取值范围没有明确规定；磁感应强度的计算方法未知，不当的方法带来过大计算量；优化算法未知，不当的优化算法同样大幅增加计算量。

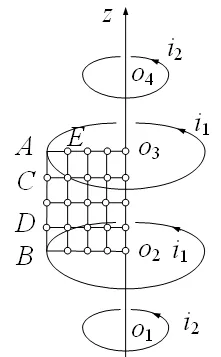
图2 磁场采样节点示意图

在以往Helmholtz线圈参数的设计过程中，计算量过大的问题往往被回避，参数设计结果被直接给出。本文将直面这一问题，并以缩减优化过程的计算量为突破口，力求高效快速地完成线圈参数设计的优化过程。下文将针对计算量的来源，从三个方面着手缩减求解问题的计算量：

(a)预估线圈参数，缩小求解范围；

(b)选取合适的采样点Bz计算方法；

(c)选取合适的优化求解算法。

2 设计难点的解决

2.1 线圈参数预估

要缩减优化过程的计算量，首先要对线圈参数最优解所在的范围进行一定的预估，缩小求解范围。

1)β1与β2的预估

考虑一种常见情形：若不考虑线圈组2对空间中磁场分布的影响，仅对线圈组1来说，在其电流大小给定的情况下，线圈轴线上的磁场分布如图3所示。并且我们已知结论：当且仅当h1=a1(即β1=1)时，线圈间磁场分布最均匀。

本题中的采样区域并非落在轴线附近，并且线圈组2的电流会对空间中的磁场产生影响，因此β1=1不是δ最小时的参数。然而可以做出一个定性的推论：当β1过大时，采样区域中的磁场分布将趋于不均匀，对线圈组2也存在类似推断。

图3 载流原线圈轴线的磁感应强度分布

结合隐含的条件β1<β2，可以预估取到最优解时应有β1<β2<5(留有一定的余量)。

2)i2的预估

题目中并未给出电流i2的正负条件，即不知道其与i1是否同向。实际上，两线圈组的电流正反向时均有可能获得一定区域内较均匀的磁场，只是获得的磁场大小均值不同。由于篇幅所限，本文选取两线圈组电流同向的情况进行求解，此时获得的匀强磁场均值较大。此时，磁场分布如图4所示。

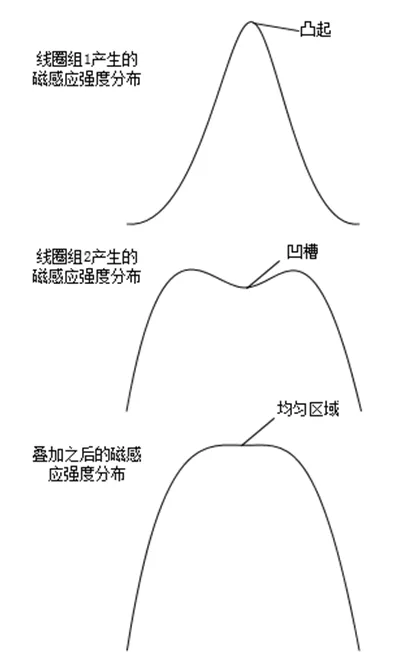
图4 两线圈组电流同向时磁场分布情况

若线圈组1线圈间距离较小，那么其叠加产生的磁场中间部分将呈“凸起”状，而线圈组2因为线圈距离较大而产生的磁场的凹槽恰好可以抹平这一尖峰，导致中间的磁场变得均匀。由于两线圈组产生的磁场起到“制约”、“抵消”的作用，两线圈组中的电流大小不会相差很大。已知i1=1 A，那么保留一定的余量，预估i2的范围是i2(0,10) A。

2.2 磁感应强度计算方法选取

1) 电流元叠加法

计算非典型模型在空间中任意点所产生的磁感应强度，可以通过电流元在空间产生磁场的Biot-Savart-Laplace Law来叠加求解：

(2)

2) 椭圆积分法

在柱坐标系下，单个载流圆线圈在空间任意点所产生的沿轴线方向的磁感应强度Bz可以通过椭圆积分法进行计算[2]。以线圈圆心为原点，轴线为z轴建立坐标系，则空间任意点z方向的磁感应强度Bz为

(3)

其中

(4)

(5)

(6)

(R为线圈半径，z、ρ为该点在柱坐标系下的z、ρ坐标，I为线圈所通电流大小)

在计算椭圆积分K(k)和E(k)的过程中，通常采取级数展开作近似计算[1]。令

m1=1-k2

(7)

则

(8)

(9)

展开式中各系数

我们选择计算更精确且计算量更小的椭圆积分法作为采样点Bz的计算方法，选择原因将在下文结合Matlab算例作详细阐述。除此之外，为了进一步缩减计算量，在编程计算各采样点的磁感应强度时，还采用矩阵运算代替for循环逐个计算，大大缩短了计算所需时间。

2.3 优化算法选取

对于优化问题，选取 Matlab软件中已有的优化工具箱Optimization toolbox作为主要的仿真求解工具。优化工具箱中目前常见的两种算法为遗传算法(Genetic Algorithm)和非线性多元函数最小值算法(Fmincon)。这两种方法的比较如表1所示。

表1 两种优化算法的优缺点

由上文已知两种优化算法的优势与局限。由于GA算法求解时不需要初值，因此考虑优化求解时先用GA算法得到较粗略的解，再将GA求出的解作为初值，利用fmincon算法快速求解出最终的最优解。这样在缩减求解计算量的同时也保证了求解的精度。

3 算例分析

3.1 两种磁感应强度计算方法比较

分别用上述的两种方法计算Bz的Matlab 算例。根据对称性，选取单个线圈轴线上的五个测试点为z=0 m，1 m，2 m，3 m，4 m并设定参数I=1 A，R=0.5 m。比较两者精确度时，通过以下已知的表达式计算出单个载流原线圈轴线上的Bz作为参考的理论值：

(10)

两种方法计算磁感应强度的精确度比较结果如表2所示。

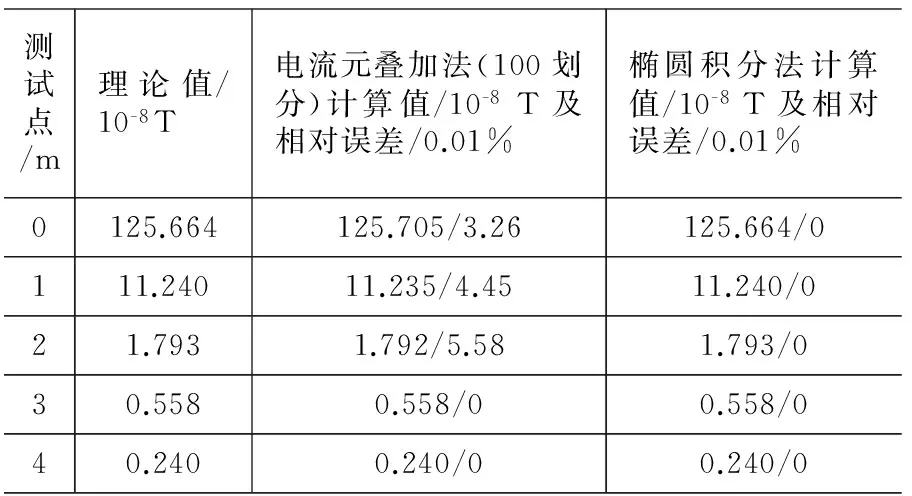
表2 两种方法计算精确度比较

(注：计算结果保留小数点后三位)

利用tic&toc计时，将不同的采样点Bz计算程序执行1000次，记录所需时间结果如表3所示。

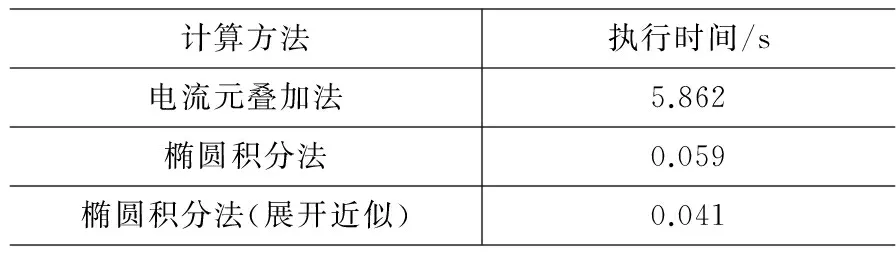
表3 两种方法计算量比较

(注：计算结果保留小数点后三位)

由两个表格中的结果可知，利用级数展开式近似计算的椭圆积分法计算量小、计算精度高，是最理想的计算方法。

3.2 基于参数设计规律的求解

由于采样点的布置对于最优解会产生影响，因此考虑在实际的求解过程中逐渐增多采样点，得到不同采样点数目下的参数最优解，探究是否存在一个较一致的参数设计规律。若存在，则可进一步验证原题目中采样20*20个点时参数设计结果的合理性。记求解的参数设计结果为[β1,β2,i2]。

首先取采样点总数，N=5*5。由于轴线附近磁场较均匀，若考察整体区域磁场的均匀性应在轴线附近少取采样点，因此设定采样点分布如图5所示，求解结果如表4所示。

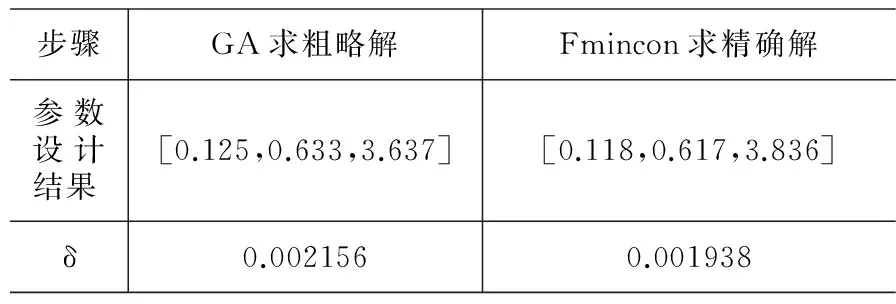
表4 N=5*5时求解结果

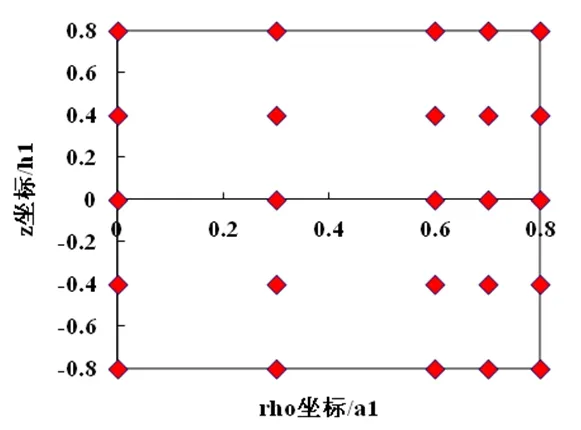
图5 N=5*5时采样点分布情况

同理，采样点总数N=9*9时采样点分布如图6所示，求解结果如表5所示。

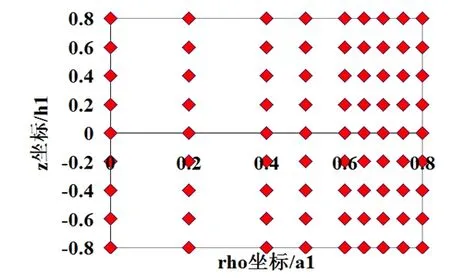
图6 N=9*9时采样点分布情况

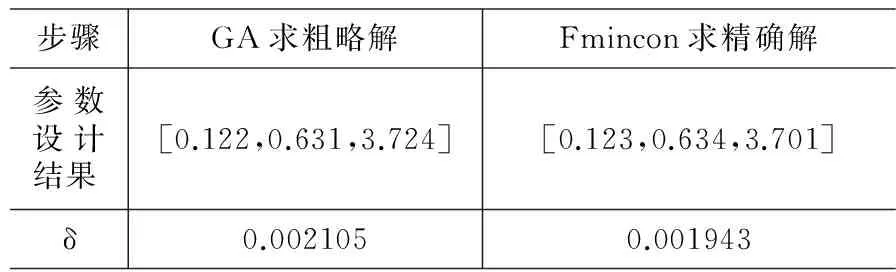
步骤GA求粗略解Fmincon求精确解参数设计结果[0.122,0.631,3.724][0.123,0.634,3.701]δ0.0021050.001943

接下来按问题要求，在关注区域中均匀采样点数为N=20*20，最终求解结果如表6所示。

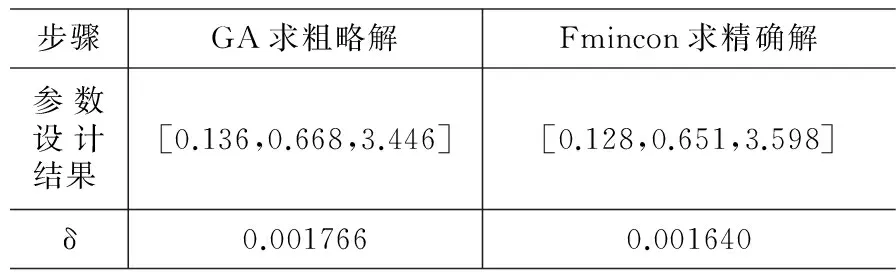
表6 N=20*20时求解结果

在采样点数目由少变多的过程中，参数设计结果变化如表7所示。

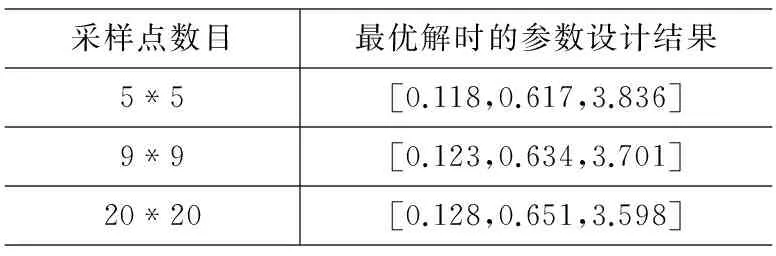
表7 采样点数目变化时的设计规律

由表中数据可以发现，不同采样点数目下的参数最优解确实存在一个较一致的规律，进一步地说明了N=20*20时所得出的参数设计结果的合理性。

当参数设计结果为[0.128,0.651,3.598]时，在关注区域内个采样点z方向磁感应强度Bz分布如图7所示。

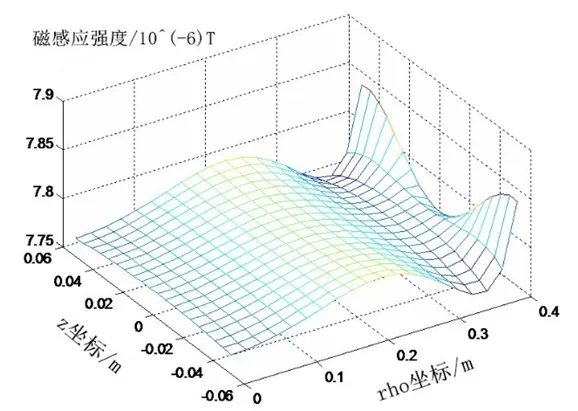
图7 关注区域内磁感应强度分布

关注区域内的磁感应强度Bzmax≈7.84×10-6T，Bzmax≈7.75×10-6T，分布极差ΔBz<10-7T，可认为区域内磁感应强度Bz分布基本均匀。

为进一步检验求解结果的正确性，求出δ关于[β1,β2,i2]的偏导数表达式，并将求解出的参数结果[0.128,0.651,3.598]代入，计算得到其偏导数结果如表8所示：

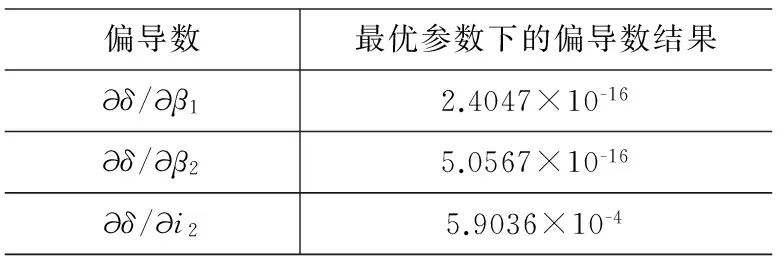
表8 最优参数下的偏导数结果

由偏导数结果可见，最优参数下偏导数均接近于零，再次证实了参数设计结果的合理性。至此，本模型中Helmholtz线圈的参数设计快速优化完成并得到了检验。

4 结语

本文研究的是利用两对Helmholtz线圈结构产生匀强磁场时的参数设计问题，提出了一种创新性的快速优化方法：通过预估参数范围、选取合理磁场计算方法及优化算法来大幅缩减求解过程中的计算量，最终实现快速优化设计的目的。

该方法的优势是显著地减少了设计线圈参数时的计算量，局限是对参数范围的理论预估较为粗糙，对线圈组中电流反向的情况尚未予分析等。

这种快速优化设计方法虽然是在Helmholtz线圈参数设计的背景下提出的，但实际上也适用于简单模型的一般性多参数优化问题，因为其核心思想是针对多参数优化过程中的计算量问题作尽可能多的缩减处理，目标是在每个环节都进行计算量的削减，最终通过软件工具快速实现对问题的求解。

[1] 马信山,张济世,王平.电磁场基础[M].北京:清华大学出版社,1995年5月

[2] 詹树军.《载流线圈外空间任意一点磁场的研究》[N].贵州:毕节学院学报,2012年第8期第30卷

[3] JIN WANG,GUOFENG LI,KE LIANG,XIANHU GAO.The Theory of Field Parameters for Helmholtz Coil[J].Modern Physics Letters B,2010, 24(2):201-209

[4] YC Guo,T Yan-Bin,XH Wen,MM Kang.Uniform magnetic field based on improved Helmholtz coils [J].Changchun:Physics Experimentation,2015,Vol.35,No.11

A Fast Optimization Method for the Helmholtz Coil Design

LIN Zhe，ZOU Jun

(ElectricalEngineeringDept.,TsinghuaUniversity,Beijing100084,China)

In this paper, the design of the Helmholtz coil used to generate a uniform magnetic field is discussed. We assess a uniform magnetic field by its nonuniformity coefficient, aiming to obtain the most uniform magnetic field. To reduce computation load, the parameters of Helmholtz coil are estimated and reasonable methods for magnetic flux density calculation and optimization are adopted when solving this multi-parameter optimization problem under the background of actual needs. Thus, a more effective and rapid method for Helmholtz coil design based on Matlab is proposed.

Helmholtz coil; uniform magnetic field; optimization of parameters

2016-02-29;

2016-05-24

林 哲(1994-)，男，本科生，研究方向为电力系统配电网，E-mail：linz13thu@163.com

TM153+.1

A

1008-0686(2017)01-0056-06