高三后进生数学学习能力的培养
徐 敏
(江苏省苏州市吴江中学,江苏 苏州 215200)
高三后进生数学学习能力的培养
徐 敏
(江苏省苏州市吴江中学,江苏 苏州 215200)
高三数学后进生的主要表现是数学学习能力低下,考试分数不高。应该从数学思维能力、逻辑推理能力、运算求解能力、阅读理解能力、规范答题能力等方面培养高三学生的数学学习能力,达到人人进步的目的。
高三;后进生;数学能力;培养
进入高三,学生的数学成绩差距很大,有些后进生除了在情感上对数学产生畏惧心理外,根本上还是因为他们的数学学习能力不强。在教学中,教师要在情感上呵护学生,更重要的是要优化教学,激发后进生的学习兴趣,培养他们的数学能力,提高他们的数学成绩,在有限的时间里,让后进生都取得巨大的进步。
一、培养后进生数学思维能力
思维能力是数学学习的基本能力。高三后进生思维能力会直接影响他们数学学习的效果。因此,教师在教学中要巧妙设计一些能激发后进生思维能力的问题,激发他们的求知欲望。
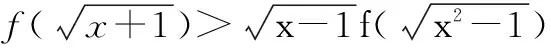

(1)设f(x)是定义在R上的增函数,则不等式f(x)>f(1)的解集是____;
(2)设f(x)是定义在R上的函数,且f′(x)>0,则不等式f(x)>f(1)的解集____;
(3)设f(x)是定义在R上的可导函数,且满足f(x)+xf′(x)>0,则不等式xf(x)>f(1)的解集____。
设计意图:让学生体会到没有解析式如何解答含有“f”的不等式——利用函数单调性的定义及定义域;由(1)铺垫,学生容易得出利用函数的导数大于0,确定函数单调递增,回到上一题解答方法。由(2)题学生能够体会到f(x)+xf′(x)>0的目的是为了说明某个函数的单调性,且这个函数一定跟xf(x)>f(1)相关,引导学生发现[xf(x)]′=f(x)+xf′(x),所以函数xf(x)在R上单调递增,由xf(x)>1f(1),从而得出答案。第(3)题的设计在第(1)(2)基础上已经有了质的飞跃,也激发了学生的数学学习兴趣,刺激他们的求知欲。
这时候回到正题,学生很容易求解。接下来进行变式训练进一步提高学生的思维能力。
变式:设f(x)是定义在R上的可导函数,f(x)>0且满足f(x)-xf′(x)>0,则不等式f(x) 教学中教师应精讲例题,巧设习题,降低或者分解题目的难度和梯度,留给后进生更多的独立时间动手动脑实践,尽可能地提供多种机会让学生自己去理解、感悟、体验,让学生有学习数学的成就感,在不知不觉中培养后进生的数学思维能力。 逻辑推理是指从一些事实和命题出发,依据逻辑规则,推出一个命题的严密的理性思维过程。推理的形式主要有合情推理和演绎推理。通过逻辑推理的培养,学生能够发现和提出命题,掌握推理的基本形式,表述论证的过程,理解数学知识之间的联系;能够理解一般结论的来龙去脉,形成举一反三的能力;能够形成有论据、有条理合乎逻辑的思维习惯和交流能力。逻辑推理能力是中学生需要具备的数学核心素养之一。 考虑到后进生的层次,为了降低题目的难度,减少抽象性,先设计习题: 方法二:考虑结果为定值,采用特值法完成,比如设P(0,2); 引领学生反思:由例题2的结论推导(*)的答案,即由一般性结论得出特殊结论。 高中数学概括性强,题目灵活多变,高三数学更是课堂容量大,为此,教师应该有意识把题目分类、对比,并反思所用知识点、解题方法和解题思路。本题讲解过程中由(*)题到例题2,培养学生概括能力和理性思考习惯,采用的是归纳推理,由例2到探究采用了类比推理,由例2到(*)采用的是演绎推理。 运算不等同于计算,运算能力也并非一种单纯的、孤立的数学能力。它需要正确理解相关知识,辨识分清运算条件,合理选择运算方法,有效设计运算步骤,还要使运算符合算律、算理,最终尽可能简洁地获得运算结果。 例3:设等差数列{an}中,a1+a2+a3=9,a3+a15=34 (1)求数列{an}的通项公式an; 分析:(1)容易解得an=2n-1 思维受阻! 不难发现学生算不出的原因是:一个方程却有两个未知量,似乎本题无法求解,甚至怀疑此题是否有问题。如何解决这个问题呢? 学生有了求解题目的方法,却不能有正确的运算来支撑,想提高数学成绩也是枉然,所以要提高后进生的数学成绩,必须培养学生算理指导下的运算求解能力。 在教学中遇到很多后进生不懂得审题,往往还没有弄清楚题目意思,就盲目做题,出现不应该发生的错误。教学中教师应该指导学生如何读题、审题,发现题目中的显性和隐性条件,及时圈点,并且在草稿纸上写下来,只有弄清楚题目的含义才有机会作出正确的解答。 对于此题,学生并不觉得难,但是做对的人却寥寥无几。 学生做错的原因主要是未注意题目中的显性和隐性条件,所以教学中教师应该引导学生如何审题,重视培养学生的阅读理解能力。 首先是规范答题顺序。一般高考题目出题顺序都是由易到难,学生答题也是由易到难,这样学生容易进入考试状态,利于学生正常发挥,但对于个别学生可能并非如此。2012年江苏数学高考卷的第15题: (1)求证:tanB=3tanA; 该题第(1)问比较容易上手,利用数量积转化为三角形的边和角的运算,再利用正弦定理化边为角;但是第(2)问很多数学成绩比较好的学生,因为这个题目耗时太长导致没有时间去做后面的会做题,结果高考失败。正确做法就要暂时放弃,学会跳跃式答题,即会做的题目认真答好,不会则跳过去,把会做的做好后,再做有可能做上的,最后是把不会的题目争取拿一点步骤分。 其次是规范答题步骤。数学解答题给分原则是按步骤得分,因此答题的规范性决定了该题的得分,所以教师在教学过程中要重视书写规范,以及对学生作业书写的规范指导。 总之,只要教师着力于课堂教学,深耕每节课,关注每个后进生的成长,他们的数学能力就会提上来,成绩也一定会得到提高。 [1]高崯.新课程要求下后进生的高中数学教学方法探讨[J].亚太教育,2015(30). [2]闫文其.如何做好高中数学教学中后进生转化工作[J].考试周刊,2014(33). [3]邱木进.如何做好高中数学教学中的后进生转化工作[J].现代教育科学:中学教师,2013(10). 〔责任编辑:李海波〕 10.3969/j.issn.1008-6714.2017.05.032 2017-03-06 徐敏(1980—),女,江苏吴江人,中教一级,从事高中数学教学研究。 G633.6 A 1008-6714(2017)05-0074-02二、培养后进生逻辑推理能力

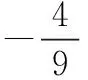
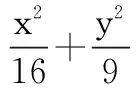
三、培养后进生运算求解能力
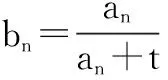
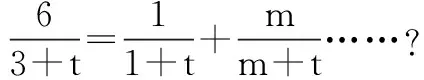
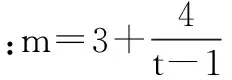
四、培养后进生阅读理解能力

五、培养后进生规范答题的能力


