基于傅立叶变换的电力系统谐波分析研究
何湘龙
(湖南石油化工职业技术学院,湖南 岳阳 414012)
基于傅立叶变换的电力系统谐波分析研究
何湘龙
(湖南石油化工职业技术学院,湖南 岳阳 414012)
利用傅立叶变换对电力系统谐波进行分析,可快捷检测到电网谐波,具有精度高、实时性好的优点,通过分析谐波检测的研究现状和发展趋势,探讨电力系统谐波的来源,提出了谐波分析与检测的方法及改进措施。
傅立叶变换;电力系统;谐波;分析
1 谐波检测的研究与意义
对电力系统谐波进行检测,可优化电能质量、提高监测效率。对电力系统谐波进行分析与检测,可从整体把握全网电能质量水平,通过对负荷公共连接点电能质量事故的检测记录与统计,可有效解决电能质量纠纷问题。
2 谐波检测的研究现状和发展趋势
近年来,计算机系统的控制设备与电子装备的应用,对电力系统谐波检测仪的发展起到了重大的推动作用,并把检测和滤波紧密地联系在一起。目前,常规的谐波测量方法主要有:模拟带通或带阻滤波器测量谐波、基于傅立叶变换的谐波测量、基于瞬时无功功率的谐波测量。在以上方法基础上,拓展方法应运而生:同步测定法、基于神经元的自适应滤波检测法[1]、基于小波变换的谐波检测方法等。未来对电力系统谐波检测方法的研究将更深入,主要有以下几个方面:第一,对检测方法的实时性、精确性、计算量、可靠性、易于实现性、自适应能力、有效范围等方面综合比较,在不同电网中采用不同的谐波检测方法。第二,从傅立叶变换到FFT,再到传统的小波变换,又到改进后的小波变换[2],这将更精确地检测出突变信号,还能更精确地分解谐波信号中的各次谐波。
随着现代控制技术的完善和多样化,基于神经元的自适应滤波检测法、基于小波变换的谐波检测方法等将成为主流。谐波测量与分析方面的发展趋势是:新的测量设备、手段会不断出现,测量方法会不断改进,最终达到网络化、智能化。
3 电力系统谐波的来源
电力系统谐波的来源一方面是非线性负荷接至供电系统,如各种整流设备、调节设备及电气拖动设备所产生的谐波电流从低压侧馈入高压侧。另一方面,供电系统本身存在非线性元件,如变压器的空载电流、可控硅控制的电容器、电抗器组等,这是造成电力网电压波形畸变的根本原因。以变压器为例,变压器的端电压为正弦波时:
(1)
于是:
(2)
i=a1φ+b1φ3
(3)
即:
(4)
由此可见,此时的电流已发生畸变,包含有3次谐波项。
4 谐波分析与检测的方法
4.1 离散傅立叶变换
离散傅立业变换的前提是对电力系统中变化波形的时间连续信号进行等间隔采样,把采样值依次转换成数字序列,借助计算机进行谐波分析。
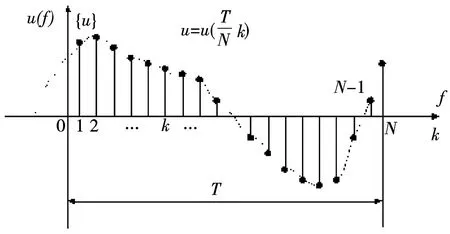
图1 周期信号的采样Fig.1 Sampling of periodic signals
(5)
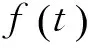
(6)
可见,离散化的实质上是把定积分计算返回近似的累加和计算,在计算机数字谐波分析中有重大的意义。式(6)是对应于(5)离散数字序列的频谱系数。由于离散化,n仅能得到0~(N-1)次的频谱,对于n>(N-1)的频谱,因式中三角函数的周期性而无限重复。

(7)

(8)
两者组成了离散傅立叶变换对。可见特定的电信号中的谐波是唯一存在的。
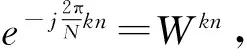
于是:
(9)
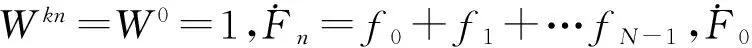

4.2 快速傅立叶变换(FFT)
傅立叶变换方法推广应用至离散系统就出现了离散采样的傅立叶变换,称为离散傅立叶变换(DFT)。该技术由于快速算法[4]的出现迅速得到发展,从而产生快速傅立叶变换(FFT),FFT已成为现代谐波测量技术和信息处理的主要数学工具。比较起来,FFT利用W的周期性和对称性来减少DFT的运算次数,加快运算速度。
4.3 窗函数与频谱泄漏
参照一般经验,选用海明窗的效果较好,海明窗:
(10)
设谐波信号加海明窗后表示为:
Xhm=X(nTs)×ωhm(n)n=0,1,2,…N-1
(11)
式中X(nTs)即信号的采样序列,Ts即采样间隔,ωhm(n)即海明窗,对此加窗后的采样序列应用FFT并进行插值算法可得到幅值和相位。海明窗算法采用的是双峰谱线插值修正算法,具体过程如下:
(12)
(13)
a=1.21874943β+0.13349531β3+ 0.05301420β5+0.03656014β7
(14)
(15)
A=N-1(y1+y2)(2.26557103+1.22719978a2+ 0.37607775a4+0.09767389a6)
(16)
A为奇次谐波系数[5]。
4.4 信号的采样
对电力系统谐波分析来讲,假设谐波频率最高为fc,那么只有满足f>2fc才能得到各次谐波对应的全部频谱。这被称为采样定理,f=2fc被成为奈奎斯特采样频率[6]。fc是电网频率50 Hz,而系统的采样频率是1 024 Hz,这样一个周期内采样N=20次,显然满足奈奎斯特采样频率。
4.5 混频现象与滤波
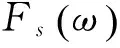
为了减少混频现象,有两种方法使离散信号真实反映相应的连续信号,一是合理选择采样周期T,采样的有效频率成分控制在0~fc,减少计算机控制系统涉及的连续信号中含有高频干扰成分的低频信号。二是在采样前,合理利用有效的低通滤波器,滤去连续信号中大于fc的高频成分。
4.6 信号复现
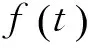
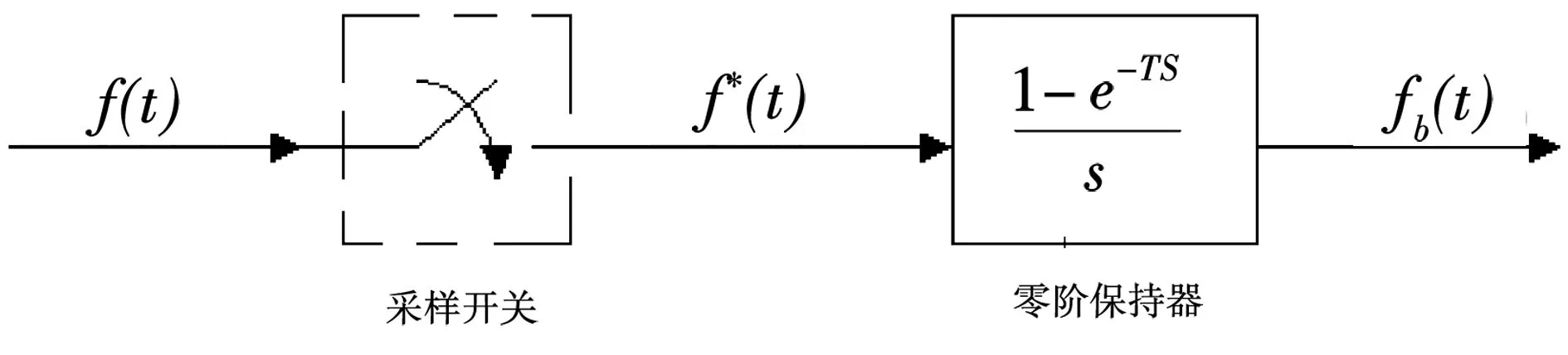
图2 S/H结构的传递函数框图Fig.2 Block diagram of transfer function of S/H structure

(17)
式中,ωc为理想滤波器的截止频率。
5 分析方法的改进
离散傅立叶变换的计算量大、运算次数多、速度慢、采样数据较多,计算程序执行时间相对较长,对数据测量的准确性和精度有一定影响。运用其他方法,比如FFT、小波分析等,利用谐波信号的周期性和对称性减少DFT的运算次数,可提高运算速度,能更精确地检测出突变信号,从而分解谐波信号中的各次谐波。
[1] 徐雷钧.一种通用电力谐波分析装置的设计[J].电测与仪表,2004,(10):88-89.
[2] 林荣文. 滤波法谐波检测技术及应用[J].电测与仪表,2004,(11):111-112.
[3] 王兆安.谐波抑制和无功功率补偿[M].北京:机械工业出版社,2008.
[4] 李益华,林文南.电力系统谐波检测的FFT加窗插值算法与小波分析方法的比较研究[J].电力科学与技术,2007,(02):55-56.
[5] 王晓亮,李娜.基于加窗插值FFT算法的间谐波检测方法研究[J].现代电力,2012,(10):71-72.
[6] 刘艳利.电力系统谐波检测算法研究与实现[D].济南:山东大学,2012.
[7] 卢惠辉.电力系统中谐波生成与检测研究[D].广州:广东工业大学,2015.
Research on harmonic analysis of power system based on Fourier transform
HE Xiang-long
(Hunan Petrochemical Vocational and Technical College,Yueyang 414012,China)
The Fourier transform is used to analyze the harmonics of power system,which can quickly detect the harmonic of the power grid. It has the advantages of high precision and real-time performance. By analyzing the research status and development trend of harmonic detection,the source of harmonic of power system is discussed,detection methods and improvement measures of harmonic analysis were proposed.
Fourier transform; Power system; Harmonic; Analysis
2016-12-20
何湘龙(1984-),男,硕士,讲师。
TM711
A
1674-8646(2017)06-0063-03

