动能定理及其应用

于洪杰

(齐齐哈尔工程学院基础部，黑龙江 齐齐哈尔 161005)



动能定理及其应用

于洪杰

(齐齐哈尔工程学院基础部，黑龙江 齐齐哈尔 161005)

在大学物理的力学研究中，一般只对质点和质点系动能定理作简要讲解，很少对其作较深入的讨论，这往往会使学生混淆概念并在理解上产生一些误区。因此，通过应用举例，对质点及质点系动能定理的理解及运用作深入的探讨，帮助学生理解动能定理，从而大大提高解题效率。

动能定理；应用；大学物理

动能定理是大学物理课程教学中的一条重要定理，为了使学生更好地理解和应用，有必要将动能定理表达式中各量的物理意义理解透彻，以便更好应用。

1 质点动能定理

1.1 质点动能定理的推导

即，外力对质点所做的功等于质点动能的增量。

应用动能定理应注意：第一，动能是状态量，功是过程量。质点的动能定理表明了质点的动能这种状态量与功这个过程量的关系。第二，动能定理适于惯性系，在不同的惯性系中，质点的位移和速度不同，列方程时，功与动能均相对同一惯性系。第三，力的线积分与积分路径无关，只与质点的起始和终了位置有关。

1.2 应用举例

如图1所示，在光滑的水平桌面上，固定着一个半径为R的半圆形屏障，一个质量为m的滑块，以速度v0沿屏障一端的切线方向进入屏障内，滑块与屏障间的摩擦系数为μ。求摩擦力所做的功。

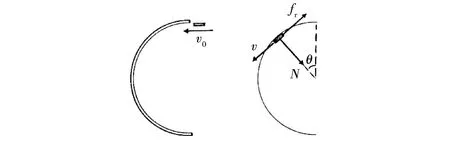
图1 滑块进入屏障示意图Fig.1 Diagram of the slider enters the barrier

解：滑块运动到任意位置受力分析如图1所示，屏的正压力为N，摩擦力f=μN，设此时速度为v，列运动方程如下：

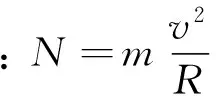
(1)

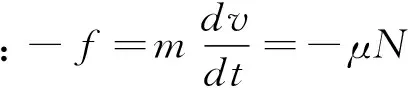
(2)

(3)

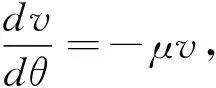
得

v=v0e-μθ

(4)

摩擦力的功有两种方法求解：

方法一：积分方法。由(2)、(3)、(4)式：

方法二：动能定理。

2 质点系动能定理

2.1 质点系的动能定理

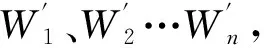
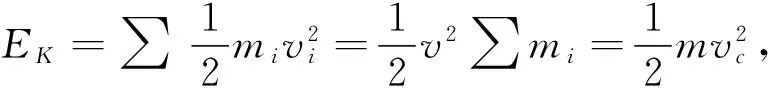
2.2 内力做功特点

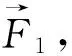
2.3 应用举例

如图2，长度为2l的均质杆件AB，重量为W，质心在C处，A为铰链连接。劲度系数为K，原长为l的弹簧，一端固结于C，另一端固结于地面上D点。当杆件AB在微小扰动下，由竖直位置运动到水平位置时。求弹簧力所做的功；杆件AB运动到水平位置时的角速度。

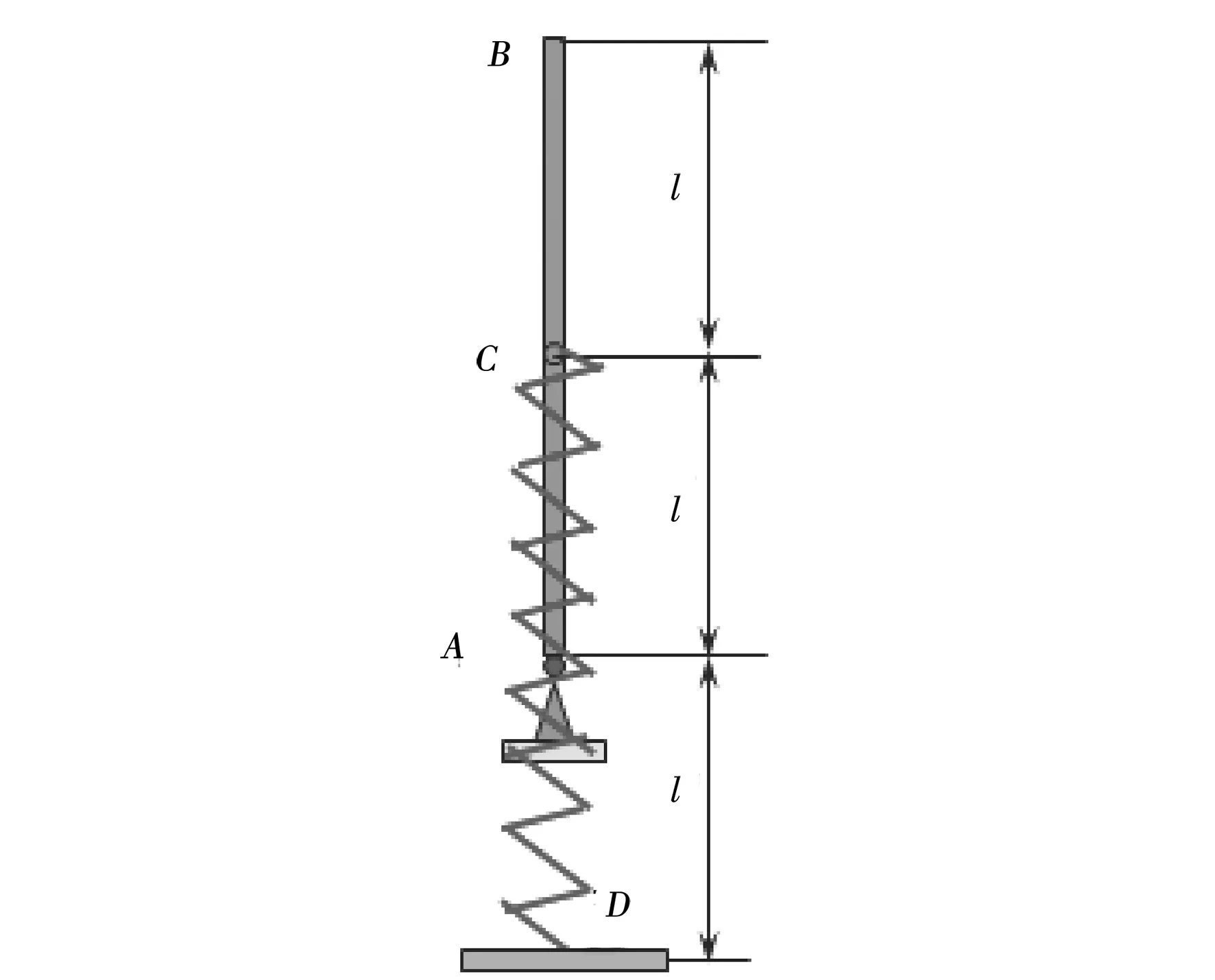
图2 杆件微小扰动示意图Fig.2 A slight disturbance of the rod

解：以AD段弹簧的长度作为弹簧原长，以A为坐标原点建立Ox坐标系。在任意坐标x处，弹簧力为F=-kx，因为弹簧力是保守力，为便于计算，弹簧力从C到C′所作的功，可以看作由C到O，再由O到C′(保守力作功与路径无关)。

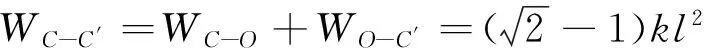
AB杆从竖直位置运动到水平位置时，不考虑摩擦力，重力W和弹簧力F做功。

应用动能定理可求得：

3 结语

动能定理是解决动力学问题的金钥匙，在教学中，恰当运用表达式处理相关问题，有助于学生理解动能定理，从而大大提高解题效率。

[1] 杨合成．关于动能定理的讨论[J]．黔江南民族师范高等专科学校学报，2002，5(1)：67-73.

[2] 马文蔚．物理学教程(上、下册)[M]．北京：高等教育出版社，2006.

Theorem of kinetic energy and its application

YU Hong-jie

(Department of Basic Science,Qiqihar Engineering College,Qiqihar 161005,China)

In the study of mechanics of university physics,only kinetic energy theorem of the particle and the system of particle have been made a brief explanation without in-depth discussion,which tends to confuse the concept and misunderstand the students. Therefore,through the application of examples,kinetic energy theorem of the particle and the system of particle were discussed in this paper to help students understanding kinetic energy theorem,thus greatly improving the efficiency of solving problems.

Theorem of kinetic energy; Application; University physics

2016-12-20

于洪杰(1983-)，女，讲师，硕士。

O313

A

1674-8646(2017)06-0046-02