基于修正Burgers模型的浇筑式沥青混合料黏弹性参数确定方法
周骜,谢发祥*,章登精,吉伯海,陈林
(1.河海大学土木与交通学院,南京210024;2.南京重大路桥建设指挥部,南京210019)
基于修正Burgers模型的浇筑式沥青混合料黏弹性参数确定方法
周骜1,谢发祥1*,章登精2,吉伯海1,陈林1
(1.河海大学土木与交通学院,南京210024;2.南京重大路桥建设指挥部,南京210019)
黏弹性是浇筑式沥青混合料的重要特性之一。首先利用Laplace变换,将修正Burgers模型的黏弹性参数转化为剪切松弛模量的Prony级数形式,以满足ANSYS等有限元软件的黏弹性材料参数输入要求,并通过ANSYS模拟验证了公式的正确性;对浇筑式沥青混合料进行了单轴贯入蠕变试验;利用Matlab软件对蠕变柔量进行拟合,获得了修正Burgers模型表征的黏弹性参数;基于推导的Prony级数公式,对单轴贯入蠕变试验进行有限元模拟,并进行了实际试验的模型应力修正。结果表明:有限元模拟结果与理论计算结果的相对误差小于1%,验证了本研究推导的Prony级数公式的可靠性;应力修正后,有限元模拟结果与试验数据的相对误差能控制在6%以内,显著提高了模型参数识别精度。
沥青混合料;黏弹性;Prony级数;修正Burgers模型;ANSYS;试验模拟
沥青路面因其平整无接缝、行车舒适性好、施工成型快、维修方便等优点,已成为中国高速公路的主要路面形式。随着公路运输量的日益增长以及交通运输向重型化发展,车辙已成为沥青路面最突出的病害[1-2]。
沥青混合料作为一种黏弹性材料,在高温下受重载后产生黏滞流动,从而产生不可恢复的残余变形。在车载的多次重复作用下,残余变形累积形成车辙。合理描述沥青混合料的黏弹性性质进而准确地预估车辙,已成为各国路面工程的一项重要课题[3-4]。
关于沥青混合料黏弹性模型的研究已有许多成果,常见的有Burgers模型以及修正Burgers模型[5-6]。对于大型通用有限元软件NASTRAN、ANSYS或者ABAQUS,设定黏弹性材料参数的常用方式是输入材料剪切松弛模量的Prony级数参数[7],这与黏弹性模型本身的参数形式不一致。基于Burgers模型的剪切模量Prony级数转化及其方法已有学者进行了相关研究[8-11],而对于修正Burgers模型的剪切模量转化方法的研究尚未见相关报道。修正的Burgers模型相比Burgers模型,因其能更为合理地解释沥青混合料的长期变形特点而在车辙模拟等领域受到广泛运用[12-14],因此进行修正的Burgers模型的Prony级数转化方法的研究,能够更好地利用有限元软件进行沥青混合料的黏弹性分析,具有理论和实际的工程意义。
1 修正Burgers模型的Prony级数形式推导与验证
1.1 修正Burgers模型的Prony级数形式推导
沥青混合料是一种黏弹性材料,在恒载作用下产生蠕变。Burgers认为,可分别用Kelvin模型和Maxwell模型表达硬化混合料的恢复性和非恢复性蠕变。将Kelvin模型和Maxwell模型串联成四单元四参数的黏弹性模型,共同描述混合料的蠕变行为,称为Burgers模型。同济大学在Burgers模型的基础上提出了四单元五参数黏弹性模型[6],如图1所示,称为修正Burgers模型。
蠕变柔量定义为,在单位应力作用下,随时间变化的应变函数。修正Burgers模型的蠕变柔量表达式如式(1)所示[5-6]。
(1)
式中:E1和E2分别为串联和并联弹簧的弹性模量,MPa;η2为并联黏壶的黏性系数;a、b为修正后串联黏壶的黏性相关系数;t为时间,s。

图1 修正Burgers模型Fig. 1 Modified Burgers model
在大型通用有限元软件中,一般通过定义非线性黏弹性材料属性的方法为输入相关材料剪切松弛模量的Prony级数[7],其剪切松弛模量的Prony级数形式为:
(2)
式中:G1为初始剪切模量,MPa;ai为相对剪切模量;ti为松弛时间,s。
蠕变方程(1)中的5个黏弹性参数不能直接作为Prony级数输入,需要将相关黏弹性参数转化为剪切松弛模量Prony参数的相关参数。
以三维形式[15-16]表示式(1):
(3)式中:G1、G2为E1、E2对应的剪切模量,MPa;n2为η2对应的三维黏性系数;A、B与a、b对应,单位分别为MPa·s和s-1,为修正Burgers模型的三维参数。
当不考虑黏弹性体积变形时[17],剪切模量与弹性模量以及其他系数的关系如下:
式中,μ为泊松比。
由黏弹性材料蠕变柔量与松弛模量间的卷积关系[10,18]可知:
(4)
对式(4)两边同时进行Laplace变换,可得[19]:
(5)

以下对修正Burgers模型松弛模量Prony级数进行推导。由式(3)的Laplace变换可以得到:
(6)
则:
(7a)
为Laplace逆变换作准备,将式(6)代入式(7a),式(7a)改写为:
(7b)
其中:
对式(7b)两边做Laplace逆变换,可以得到:
Y(t)=2 (q1+q2e-αt+q3e-βt)
(8)
则:
(9)
这样就可以获得在有限元软件中(如ANSYS)要求输入的材料Prony级数参数为:
(10)
1.2Prony级数转化公式的有限元算例验证
为验证修正Burgers模型的Prony级数推导结果的正确性,本研究建立了如图2所示的ANSYS有限元模型。单元类型为SOLID185,单元大小1m×1m×1m,共1个单元,8个节点。本算例取表1中的修正Burgers模型参数作为材料属性,并通过上节的方法计算求得对应的Prony级数。边界条件如图2所示,施加均布荷载0.7MPa。

表1 算例材料属性Table 1 Material properties of the calculation example

图2 ANSYS模型示意图Fig. 2 Schematic diagram of ANSYS model
将ANSYS模拟所得的节点应变数据转化为蠕变柔量,并与修正Burgers模型的理论计算结果进行对比,结果见表2。由表2可知,有限元模拟结果与理论计算结果一致,相对误差小于1%,计算结果表明本研究推导的Prony级数结果是可靠的,可以通过此方法将黏弹性材料的材料参数准确地输入有限元软件。但是,本数值模拟单元受力均匀,与实际蠕变贯入试验有较大差异。

表2 公式计算结果与ANSYS模拟对比Table 2 The comparison between formula calculation and the ANSYS simulation results
2 单轴贯入蠕变试验与有限元模拟
2.1 沥青混合料单轴贯入蠕变试验
为获得特定沥青混合料的黏弹性参数,进行了沥青混合料的单轴贯入试验,如图3所示。该试验方法是评价沥青混合料抗剪切能力大小的有效方法[20-22]。本研究进行的单轴贯入试验采用30 cm×28 cm×5 cm车辙板试件,级配组成见表3。试验采用WANCE材料试验系统进行,压头直径100 mm,施加0.7 MPa恒定荷载,分别在40,50和60℃恒温下进行试验。实验在试件中心轴向施加一瞬时荷载,并保持这个荷载大小不变,测量试件随时间变化的位移数值。考虑到试件在荷载作用下的变形较小,由位移数据可得到应变数值,并采用压头荷载计算,可以得到近似的混合料蠕变柔量数值。

图3 沥青车辙板单轴贯入试验Fig. 3 The uniaxial penetration test on gussasphalt plate

表3 浇筑式沥青混合料级配组成Table 3 Gradation of used gussasphalt in this study
采用Matlab软件对蠕变柔量进行拟合,并对各参数进行迭代求解。采用上节所述的Prony推导方法,取混合料泊松比为0.25,拟合结果与对应的Prony级数如表4所示。

表4 实验数据拟合结果Table 4 Fitting results of experimental data
2.2 贯入试验有限元模拟与修正
采用表4中的材料参数,建立单轴贯入蠕变试验的有限元模型,结果如图4所示。模型尺寸为30 cm×28 cm×5 cm,单元类型SOLID185。圆形加载区域位于模型中央,直径10 cm,同时在加载区域与模型边界之间设置过渡区,直径18 cm。边界条件为:底面受到竖向约束,底面四角受到三向约束。对中央圆形加载区域施加0.7 MPa恒定面荷载,结果如图5所示(以40℃为例)。由图5可知,有限元模拟结果与试验结果有较大差距。对有限元模拟结果的竖向应力进行分析,如图6、图7所示。由图6、图7可知,在加载面下方区域,竖向应力沿宽度方向有一定程度的缩减,即沥青材料受到的真实竖向应力显著小于试验加载。通过提取模型加载面下方圆柱形区域的应力,得到该区域竖向主应力(Z方向)均值随时间变化的曲线,如图8所示。由图8可知,加载面下方区域的竖向应力均值随时间变化很小,变化幅度小于1%,可近似取为0.593 MPa。引入修正系数α(此处α为1-0.593/0.7=15.3%)对试验的竖向应力进行修正,得到新的试验材料参数,如表5所示。

图4 单轴贯入蠕变试验有限元模型Fig. 4 The finite element model of uniaxial penetration creep test

图5 修正前后有限元结果与试验结果对比(40℃)Fig. 5 Comparison between the finite element simulation and experimental results before and after correction(40℃)
(11)
式中:p1为试验时加载的压强,MPa;p2为试验时加载的压强,MPa。
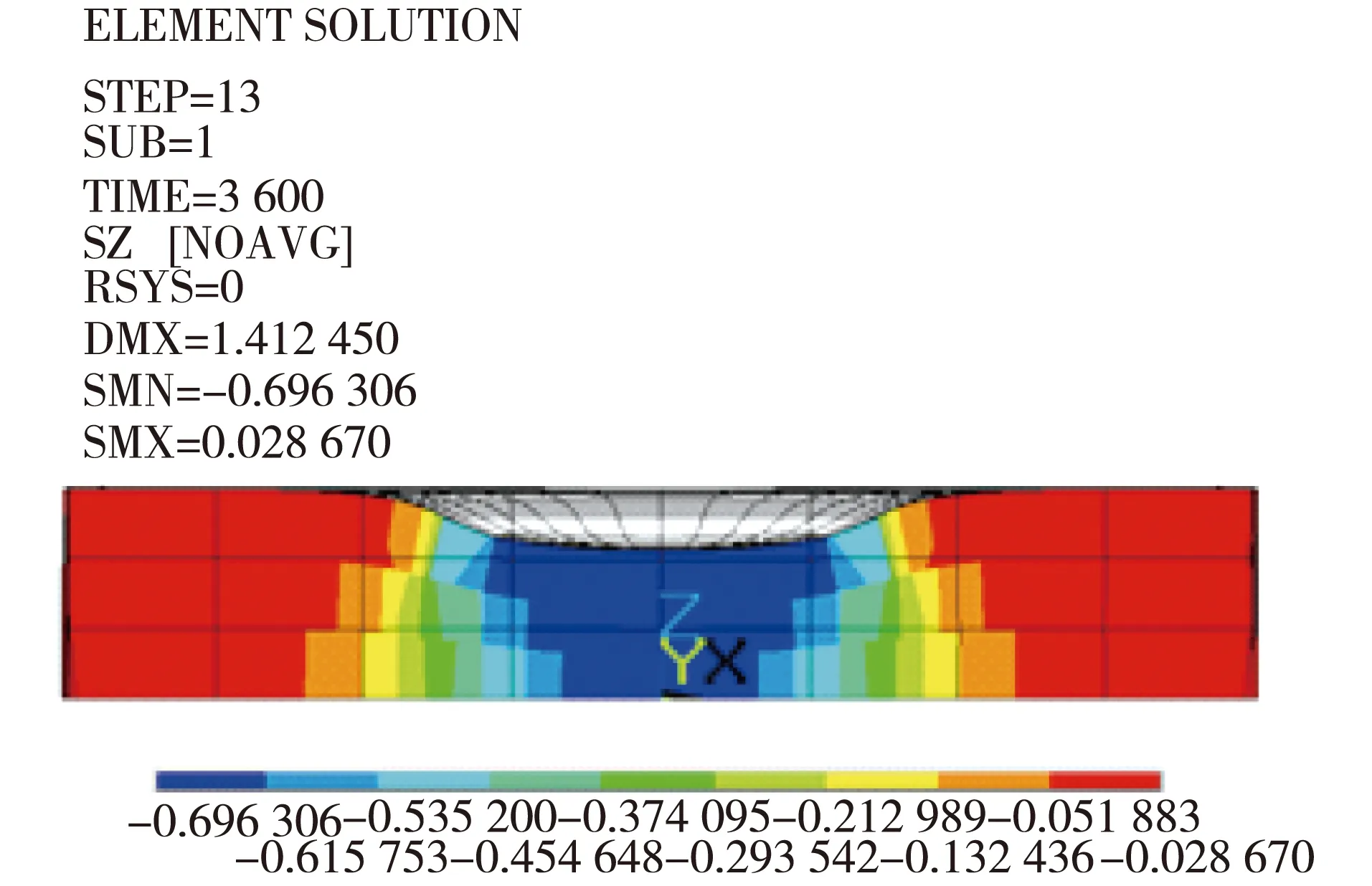
图6 中央剖面竖向应力云图Fig. 6 Vertical stress cloud of central section

图7 加载区域下方竖向应力分布Fig. 7 Distribution of vertical stress under the loading area

图8 竖向应力均值时程Fig. 8 Time history of mean value of vertical stress

温度/℃修正Burgers模型参数Prony级数参数(剪切模量)E1/MPaE2/MPaη2/(MPa·s)a/(MPa·s)b/sa1t1a2t2应力修正系数/%4074832952680×104153×104362×10-301411671906896331535061002198503×104108×104547×10-30219846706176421536049911797384×104818×103547×10-3019947950637266153

图9 不同温度(50℃(左)60℃(右))下修正前后有限元结果与试验结果对比Fig. 9 Comparison between the finite element simulation and the experimental results before and after correction at 50℃(left) or 60℃(right)
采用应力修正后的材料参数,重新对试验进行有限元模拟,结果如图5、图9、图10所示。由图5、图9、图10所示的对比结果可见,引入修正系数后,不同温度下贯入试验的有限元模拟精度均大幅提高。修正后有限元模拟的相对误差在6%以内,与试验结果吻合度良好。实际上,本研究通过一次修正以后的结果已经能够满足工程需要,如果不能满足要求,可以按照本研究所述的方法进行二次修正,提高模型参数识别精度。

图10 不同温度(40℃(左)50℃(中)60℃(右))下修正前后相对误差对比Fig. 10 Comparison of relative error before and after correction at 40℃(left),50℃(middle) or 60℃(right)
3 结 论
本研究进行了浇筑式沥青混合料单轴贯入蠕变试验,推导了修正Burgers模型的黏弹性参数的Prony级数形式,通过有限元计算验证了公式的正确性,并提出了提高模型参数识别精度的应力修正方法,通过研究得到了以下结论:
1)结合修正Burgers模型本构关系,提出了修正Burgers模型剪切模量的Prony级数推导方法及相关参数的转换公式。通过有限元模型算例,验证了修正Burgers模型剪切模量的Prony级数转换公式的正确性。
2)通过应力分析,提出了沥青混凝土单轴贯入蠕变试验的模型参数识别的修正方法,通过应力修正系数改进沥青混合料黏弹性参数识别结果,大幅提高了有限元模拟与试验的吻合度。
[1]郜玉兰, 赵队家, 韩萍, 等. 重载交通下山区高速公路车辙病害原因分析及对策[J]. 公路, 2011(1):114-118. GAO Y L, ZHAO D J, HAN P, et al. The causes and countermeasures of the rutting damage of the expressway in the mountain area under heavy load traffic[J]. Highway, 2011(1):114-118.
[2]申爱琴, 王娜, 李明国, 等. 高速公路SMA混合料高温稳定性及影响因素[J]. 长安大学学报(自然科学版), 2006, 26(1):1-7. SHEN A Q, WANG N, LI M G, et al. High temperature stability and its influencing factors of SMA mixture[J]. Journal of Chang’an University(Natural Science Edition), 2006, 26(1):1-7.
[3]MARASTEANU M, CLYNE T, MCGRAW J, et al. High-temperature rheological properties of asphalt binders[J]. Transportation Research Record:Journal of the Transportation Research Board, 2005(1901):52-59.
[4]JONES R, HORNER D, SULLIVAN P, et al. A methodology for quantitatively assessing vehicular rutting on terrains[J]. Journal of Terramechanics, 2005, 42(3):245-257.
[5]吴礼贤, 彭小芹. 修正的Burgers模型及其对于硬化混凝土的应用[J]. 重庆建筑工程学院学报, 1990,12(1):38-43. WU L X, PENG X Q. Modified Burgers model and its application to hardened concrete[J]. Journal of Chongqing Jianzhu University, 1990, 12(1):38-43.
[6]徐世法, 朱照宏. 按粘弹性理论预估沥青路面车辙[J]. 同济大学学报, 1990,18(3):299-305. XU S F, ZHU Z H. Prediction of rutting of asphalt pavement by viscoelastic theory[J]. Journal of Tongji University(Natural Science), 1990, 18(3):299-305.
[7]王新敏. ANSYS工程结构数值分析[M]. 北京:人民交通出版社, 2013. WANG X M. Numerical analysis of ANSYS engineering structure[M]. Beijing:China Communication Press, 2013.
[8]陈静云, 周长红, 王哲人. 沥青混合料蠕变试验数据处理与粘弹性计算[J]. 东南大学学报(自然科学版), 2007, 37(6):1091-1095. CHEN J Y, ZHOU C H, WANG Z R. Data processing and viscoelastic computation for creep test of asphalt mixture[J]. Journal of Southeast University(Natural Science Edition), 2007, 37(6):1091-1095.
[9]郭乃胜, 赵颖华. 动荷载作用下纤维沥青路面的黏弹性响应[J]. 沈阳建筑大学学报(自然科学版), 2007, 23(6):922-925, 929. GUO N S, ZHAO Y H. Viscoelastic response of fiber reinforced asphalt pavement subjected to dynamic load[J]. Journal of Shenyang Jianzhu University(Natural Science), 2007, 23(6):922-925, 929.
[10]蒙上阳, 唐国金, 雷勇军, 等. Burgers模型的参数获取方法[J]. 固体火箭技术, 2003, 26(2):27-29, 45. MENG S Y, TANG G J, LEI Y J, et al. Method of obtaining the burgers model parameters[J]. Journal of Solid Rocket Technology, 2003, 26(2):27-29, 45.
[11]王丰胜. 基于Burgers 黏弹性模型的沥青路面蠕变变形规律三维有限元分析[J]. 工业建筑, 2014, 44(3):104-109. WANG F S. A 3D Fem analysis of creep deformation law of asphalt pavement based on Burgers viscoelastic model[J]. Industrial Construction, 2014, 44(3):104-109.
[12]易富, 高健, 金艳, 等. 考虑蠕变固结的高温沥青路面响应仿真[J]. 辽宁工程技术大学学报, 2014, 33(11):1480-1483. YI F, GAO J, JIN Y, et al. Analysis of high temperature asphalt pavement response considering the creep consolidation [J].Journal of Liaoning Technical University(Natural Science), 2014, 33(11):1480-1483.
[13]董满生, 鹿婧, 凌天清, 等. 考虑温度效应的沥青混合料参数模型[J]. 工程力学, 2016, 33(6):180-185,193. DONG M S, LU J, LING T Q, et al. Parametric model for asphalt mixtures considering temperature effect[J]. Engineering Mechanics, 2016, 33(6):180-185,193.
[14]李国芬, 王宏畅, 王勇, 等. 基于修正Burgers模型的钢桥面铺装车辙有限元分析[J]. 林业工程学报,2016, 1(5):120-125. LI G F, WANG H C, WANG Y, et al. Finite element analysis of steel bridge deck pavement rut based on modified burgers model[J]. Journal of Forestry Engineering, 2016, 1(5):120-125.
[15]任瑞波, 郭大智. 层状黏弹性体系力学[M]. 哈尔滨:哈尔滨工业大学出版社, 2001. REN R B, GUO D Z. Mechanical layered viscoelastic system[M]. Harbin:Harbin Institute of Technology Press, 2001.
[16]邵俊华. 玻璃纤维沥青混合料粘弹性分析及参数确定[D]. 吉林:吉林大学, 2008. SHAO J H. Viscoelastic analysis and parameter determination of glass fiber asphalt mixture[D]. Jilin:Jilin University, 2008.
[17]潘晓明, 余俊, 杨钊, 等. 一种将线性粘弹微分型本构方程应用到ABAQUS的方法[J]. 华侨大学学报(自然科学版), 2010, 31(5):570-575. PAN X M, YU J, YANG Z, et al. A method using linear viscoelastic differential constitutive equation into ABAQUS[J]. Journal of Huaqiao University(Natural Science), 2010, 31(5):570-575.
[18]黄文柯, 张丽娟, 张肖宁,等. 沥青混合料蠕变柔量转换为松弛模量的研究[J]. 交通科学与工程, 2015, 31(3):7-12. HUANG W K, ZHANG L J, ZHANG X N, et al. Research on the relaxation modulus converted to creep compliance of asphalt mixture[J]. Journal of Transport Science and Engineering, 2015, 31(3):7-12.
[19]吕慧杰, 刘涵奇, 罗蓉. 基于单轴压缩蠕变试验求解沥青混合料松弛模量[J]. 武汉理工大学学报(交通科学与工程版), 2016, 40(6):1067-1072. LYU H J, LIU H J, LUO R. Determination of relaxation modulus of asphalt mixtures using uniaxial compressive creep test[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2016, 40(6):1067-1072.
[20]毕玉峰, 孙立军. 沥青混合料抗剪试验方法研究[J]. 同济大学学报(自然科学版), 2005, 33(8):1036-1040. BI Y F, SUN L J. Research on test method of asphalt mixture’s shearing properties[J]. Journal of Tongji University(Natural Science), 2005, 33(8):1036-1040.
[21]谭巍, 周刚. 沥青混合料高温稳定性的单轴贯入试验研究[J]. 石油沥青, 2009(2):14-18. TAN W, ZHOU G. Applying the uniaxial penetration text method to study thermal stability of asphalt mixtures[J]. Petroleum Asphalt, 2009(2):14-18.
[22]张宏. 沥青路面数值模拟及单轴贯入蠕变试验研究[D]. 重庆:重庆交通大学, 2008. ZHANG H. A research on numerical simulation and uniaxial penetration creep text asphalt pavement[D]. Chongqing: Chongqing Jiaotong University, 2008.
Viscoelastic parameters determination method of pouringtype asphalt mixture based on modified Burgers model
ZHOU Ao1, XIE Faxiang1*, ZHANG Dengjing2, JI Bohai1, CHEN Lin1
(1. College of Civil and Transportation Engineering, Hohai University, Nanjing 210024, China;2. Nanjing Public Infrastructure Construction Center, Nanjing 210019, China)
Viscoelasticity is one of the important characteristics for gussasphalt. The objective of this study is to find the correct viscoelastic material parameters for the novel gussasphalt applied in the 4th Changjiang (Yangtze) River Bridge based on the modified Burgers model. In this study, we first converted the viscoelastic parameters of modified Burgers model into the explicit Prony series form of the shear relaxation modulus using the Laplace transform. Thus they could be transformed into the required material parameters that were used to input into the finite element software such as ANSYS, and the correctness of the formula was verified by ANSYS simulation. At the same time, the uniaxial penetration creep experiment of gussasphalt was carried out at constant temperature of 40, 50, and 60℃, respectively. The creep compliance was fitted by Matlab program, and the viscoelastic parameters were obtained by modified Burgers model, respectively. Based on the explicit Prony series formulas developed in this study, the uniaxial penetration creep experiment was simulated by finite element software. Based on the analysis of the vertical normal stress in the actual experimental model, the stress correction coefficientαwas presented to carry out the stress correction in the model, and the viscoelastic material parameters with higher accuracy were obtained at different temperature. The results indicated that the relative error between the finite element simulation and the theoretical calculation is lower than 1%, which validated the reliability of explicit Prony series formula deduced in this study. After the stress correction, the relative error between the finite element simulation and the experimental data could be controlled within 6%, which significantly improved the accuracy of model parameter identification.
asphalt mixture; viscoelasticity; Prony series; modified Burgers model; ANSYS; experiment simulation
2016-12-28
2017-02-17
国家自然科学基金(51478163);江苏省自然科学基金青年项目(BK2012412);中央高校基本科研业务经费专项资金(2015B17614);浙江省交通科学计划(2014W01,2014H27)。
周骜,男,研究方向为钢桥疲劳、维护及长效管理。通信作者:谢发祥,男,副教授,博士。E-mail:xiefaxiang@gmail.com
U416.2
A
2096-1359(2017)03-0143-07

