生物质固体成型燃料热值和碳元素预测模型的建立＊

关雎，聂淑瑜

(广州能源检测研究院，广州 511447)

生物质固体成型燃料热值和碳元素预测模型的建立＊

关雎，聂淑瑜

(广州能源检测研究院，广州 511447)

建立生物质固体成型燃料热值和碳元素预测模型。利用秸秆类生物质固体成型燃料的测试数据，以工业分析中的水分、灰分、挥发分和固定碳含量指标为4个自变量，分别以低位热值、高位热值和碳元素分析为因变量，通过多元线性回归模型(MLR)方法建立多元线性回归预测模型。内部检验和外部检验说明3组模型在应用域范围内均具有理想的预测能力，拟合效果良好，其中高位热值预测模型的R2和R2prep分别为0.900和0.730，与已有研究相比，相对残差范围减小为–2.59%～2.26%，可为工业用途的生物质固体成型燃料的热值和碳元素分析快速做出反映。

生物质固体成型燃料；热值；碳元素；多元线性回归；预测模型

随着世界经济的飞速发展，石化能源消耗量急剧增加，人类的可持续发展受到严重影响。积极开发利用可再生清洁能源、减少石化能源消耗、降低温室气体排放，已经成为世界各国缓解能源危机和气候变化问题的共识［1］。生物质能是继煤和石油之后的世界第三大能源，生物质燃料既能缓解温室效应，又能充分利用废弃生物质资源，具有明显的社会意义与经济意义。目前，生物质能应用广泛，其中生物质固体成型燃料是生物质固体形态的能源化利用方式，也是生物质能源化利用最简单、最直接的途径之一［2–3］。

由于生物质固体成型燃料的组成成分各异，导致其具有参差不齐的物化特性。生物质固体成型燃料的物化特性通过生物质的热值、工业分析和元素分析得到反映，这3项指标作为生物质燃料质量的优劣及其工业用途的重要参考依据。与工业分析相比，生物质燃料热值和元素分析测试的操作过程复杂，耗时长，容易受到外界环境温度变化的影响，对检测人员的水平要求甚高。此外，由于生物质固体成型燃料被广泛用作工业燃料，入厂前需对其进行分批分量的常规分析，工作量巨大，因此寻求便捷的定量分析方法尤为必要。目前国内外虽有生物质固体成型燃料工业分析和元素分析指标之间定性关系的初步研究［4–5］，但利用数学方法来定量分析生物质固体成型燃料的热值和元素分析指标的研究甚少。笔者基于秸秆类生物质固体成型燃料的测试数据(工业分析、低位热值、高位热值及碳元素分析指标)，以工业分析中的水分、灰分、挥发分和固定碳含量指标作为自变量，分别以低位热值、高位热值和碳元素分析为因变量，用多元线性回归模型(MLR)方法建立多元线性回归方程，通过内部检验和外部检验判断模型的预测能力，并使用Leverage方法定义模型的应用域。本研究对生物质固体成型燃料理化特性之间定量关系的探索具有参考价值，为生物质固体成型燃料的低位热值和高位热值、碳元素分析指标提供了一种简单快速的计算方法，对工业用途的生物质固体成型燃料的热值和元素分析快速做出反映具有重要意义。

1 建模数据与方法

1.1 建模数据获取

按照GB／T 21923–2008 《固体生物质燃料检验通则》、GB／T 28731–2012 《固体生物质燃料工业分析方法》和GB／T 30727–2014 《固体生物质燃料发热量测定方法》等国家标准，对2016年10月和11月送往广州能源检测研究院检验的生物质固体成型燃料(均为秸秆类生物质)样品的水分、灰分、挥发分和固定碳，低位热值和高位热值以及元素分析中的空气干燥基碳含量等指标进行检测。其中35组数据用于构建多元线性回归方程，为训练集(training set)；7组数据用于验证方程，为测试集(test set)，试验数据见表1、表2。

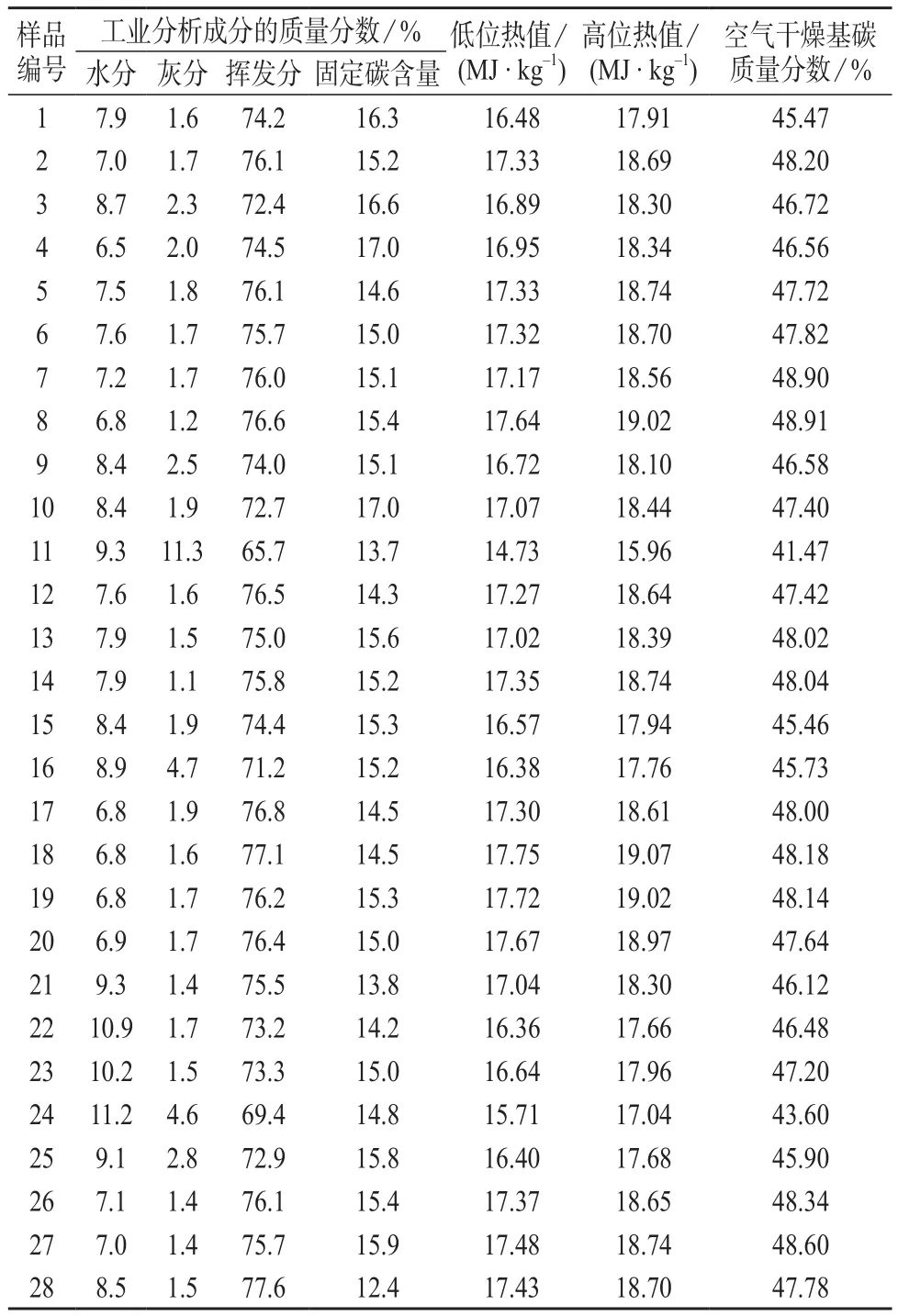
表1 生物质固体成型燃料样品的特性分析检测数据(训练集)

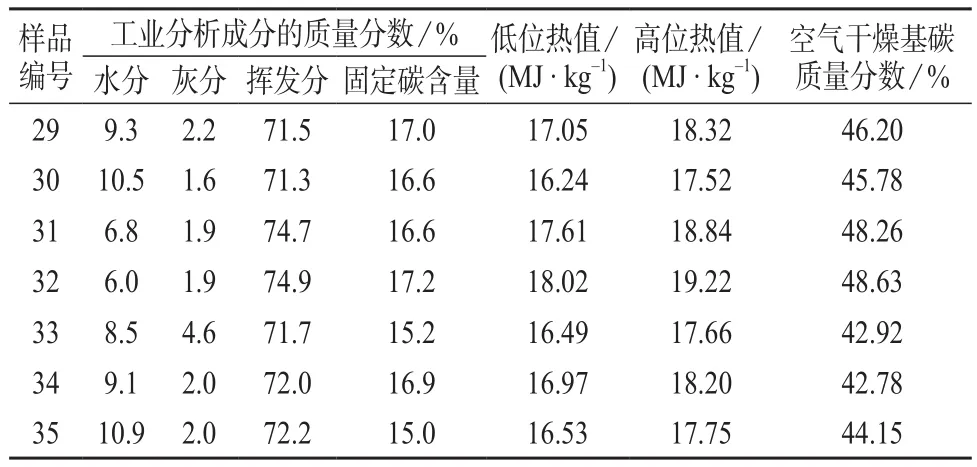
续表1

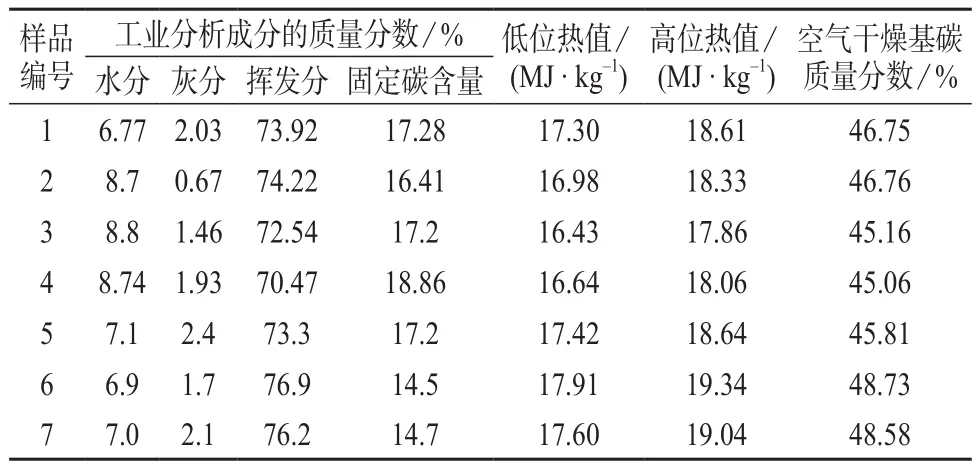
表2 生物质固体成型燃料样品的特性分析检测数据(测试集)

1.2 建模方法

多元线性回归模型(MLR)具有形式简单、表达清晰、易于解释等特点，并且能够在描述值和实验值之间建立明确的方程，是定量构效关系研究及数据预测最为常用的建模方法之一［6］。笔者采用MLR方法构建秸秆类生物质固体成型燃料热值和碳元素的预测模型。MLR方法可表示如下［7］。

设Y为可观测的随机变量，本实验代表低位热值、高位热值或者空气干燥基碳含量。Y受N个非随机因素X1，X2，…，XN(本实验为4项工业分析指标)和随机因素的影响，则Y与X1，X2，…，XN的线性关系见式(1)。

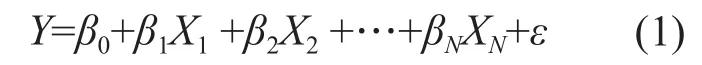
式中：β0，β1，…，βN——N+1个未知系数；

ε——不可测量的随机误差，通常假定ε～N(0，σ2)。

应用SPSS统计分析软件，通过35组训练集数据，以生物质固体成型燃料的4项工业分析指标为自变量，分别建立生物质固体成型燃料的低位热值、高位热值和空气干燥基碳含量3个指标的多元线性回归方程。

1.3 模型验证

为了建立一个拟合度高、稳定性和预测能力强的可靠预测模型，一般需要采用多种方法对模型进行评估［8］，主要包括模型的内部拟合度、内部预测能力、模型的显著性、模型内参数的显著性和模型的外部预测能力等的评估。主要通过模型的内部拟合度显著性(F检验)及外部预测能力这3项指标来分析已建立的多元线性回归方程的预测能力。

R2是描述对模型贡献的全变差分数，R2值越接近1.0，回归方程就越能够更好地表示Y变量。它是最常用的内部检验指标，能很好地反映模型的内部拟合度，R2按式(2)计算。

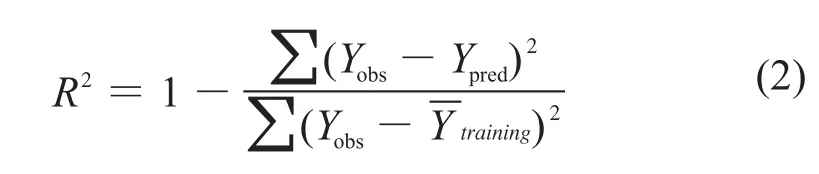
模型及参数显著性检验，F检验(Ftest)［9］：Fisher统计或方差比是检验自变量和因变量之间的线性回归方程是否显著的重要方法，适用基于多元线性回归方法建立的模型。对于多元线性回归模型，在对每个回归系数进行显著性检验之前，应该对回归模型的整体做显著性检验，这就是F检验。如果是显著的，说明两个变量之间存在线性关系，如果不显著，则说明两个变量之间不存在线性关系。

对所建模型进行内部验证后还必须进行外部验证，外部验证能为模型预测能力提供一个更加严厉的评估。使用不参与建模的外部测试集(见表2)进行外部验证。R2prep参数是用来评估模型的外部预测能力一个非常重要的指标参数［10］。R2prep定义为建立模型的预测性复相关系数，按式(3)计算。

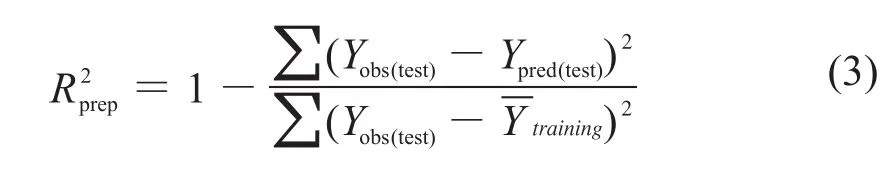
一般情况下，(1)当R2＞0.6，R2prep＞0.5时，认为模型好，大于0.9则为模型优秀。Tropsha等建议R2和R2prep均大于0.6［11］。

通过已建立的多元线性回归方程，用表2中7组测试集的工业分析指标数据对生物质固体成型燃料的低位热值、高位热值和空气干燥基碳含量进行预测，并使用模型内部检验参数、F显著性分析及外部检验参数R2prep对模型进行评估，反映生物质固体成型燃料热值和碳元素含量计算模型的预测能力。

1.4 模型的应用域

经过内部验证和外部验证后，即使各项评价指标都证明所建模型是稳健、可靠且具有很好的泛化能力和预测能力，还不能认定该模型能对任何未知样本做出可靠的预测［12］。因此必须定义多元线性回归方程的应用域［13］。如果预测样本不在模型的适用范围内，则模型对该样本的预测不一定可靠［12］。定义应用域的一个简单方法是确定外推程度［14］，通过杠杆值hi反映外推的程度。

对模型应用域的定义一般使用leverage方法［14］。该方法的优点是可以将模型的应用范围量化，并用直观图形的方式表达出来，即Williams图。标准的leverage值定义为h*=3p'／n(p'为模型中所使用描述符的个数加l，n为训练集样本的个数)。根据式(4)计算每个样本的leverage值hi。

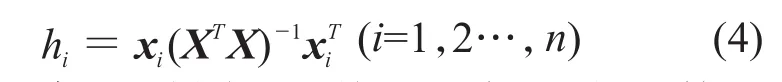
式中：xi——待预测样本i的特征矩阵(即描述符矩阵)；

X——全体训练集样本的特征矩阵；

n——待预测样本的个数。

Williams图就是以leverage值为横坐标，以标准残差为纵坐标构建的。在Williams图中，两条水平线±3表示设定的标准残差的标准，垂直的线表示h*值，只有落在这3条线围成的区域，即h≤h*，标准残差在±3范围内的样本才认为是符合模型的应用域，其预测值才是可靠的［15］。单个样本的标准残差按式(5)计算。

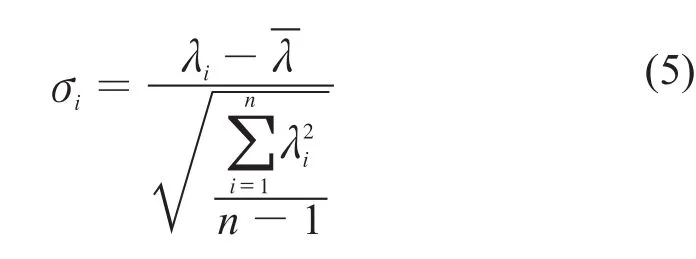
其中：σi——第i个预测样本的标准残差；

λi——第i个预测样本的残差，即第i个样本

的预测值与实测值之差；

——所有预测样本的残差的平均值。

2 结果与讨论

2.1 模型建立与预测能力评估

已有研究表明，热值和空气干燥基碳含量与生物质固体燃料的4项工业分析指标均呈现较高的相关性显著水平［7］，因此以表1中35组样本为训练集，分别以低位热值、高位热值和空气干燥基碳含量为因变量，自变量均为4项工业分析指标，即水分、灰分、挥发分和固定碳含量。通过SPSS统计分析软件，得到三个多元线性回归方程，结果见表3。

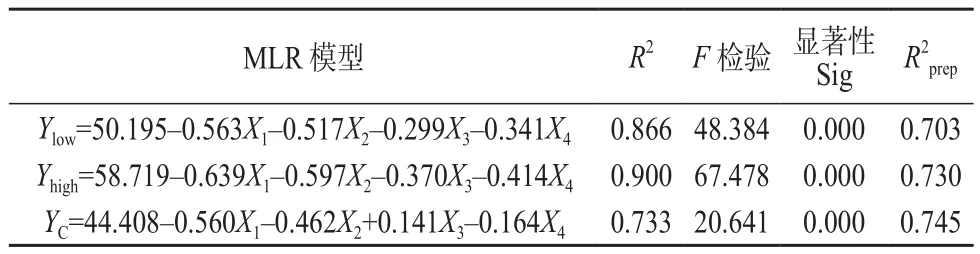
表3 低位热值、高位热值和空气干燥基碳含量的预测模型与统计参数

为了检验多元线性回归方程的预测能力，通过模型的内部检验参数R2和F检验，外部检验参数R2

prep来分析，结果见表3。对于低位热值的MLR模型Ylow，内部检验参数R2和F检验计算结果分别为0.866和48.384，反映了模型较好的拟合能力。对于高位热值的MLR模型Yhigh，内部检验参数R2和F检验计算结果分别为0.900和67.478，说明模型具有很好的拟合能力。对于空气干燥基碳含量的MLR模型YC，内部检验参数R2和F检验计算结果分别为0.733和20.641，说明训练集中的样本能够很好的被预测。另外，3个MLR模型的显著性Sig值均为0.000(小于0.05)，说明模型具有较好的稳健性，排除了偶然得到的可能性。综合多元线性回归预测模型的内部检验指标，说明预测模型具有良好的拟合能力。

除了对所建立的预测模型进行内部检验，还必须对模型进行外部检验，外部检验可以更显著地反映出模型的预测能力。外部检验需要用不参与建模的数据集，即表2中的测试集数据进行检验。通过R2

prep值分析模型的外部预测能力，其计算按照式(3)。生物质固体燃料低位热值、高位热值和空气干燥基碳含量对应的MLR模型的R2prep计算结果分别为0.703、0.730和0.745，均大于0.6，进一步说明了模型具有很好的预测能力。此外，R2–R2prep＜0.3，排除了模型有过拟合嫌疑或数据有离群值的可能性［16］。

2.2 模型预测效果分析

利用所建立的多元线性回归方程，对生物质固体燃料测试集的7组数据(表2)进行模型预测效果分析。分别作出低位热值、高位热值和空气干燥基碳含量对应3个MLR模型预测值和实测值的曲线图，并对分析预测值与实际测量值的绝对残差和相对残差进行误差分析，结果见图1～图3。

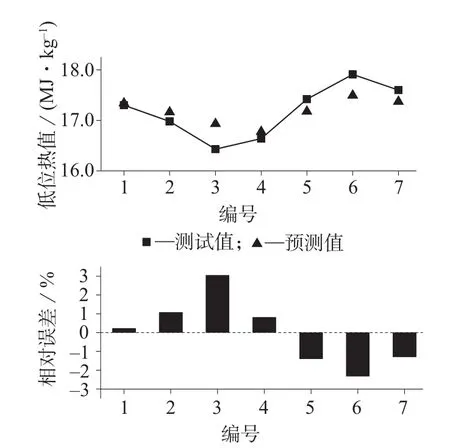
图1 生物质固体燃料低位热值的实测值与预测值对比及相对误差

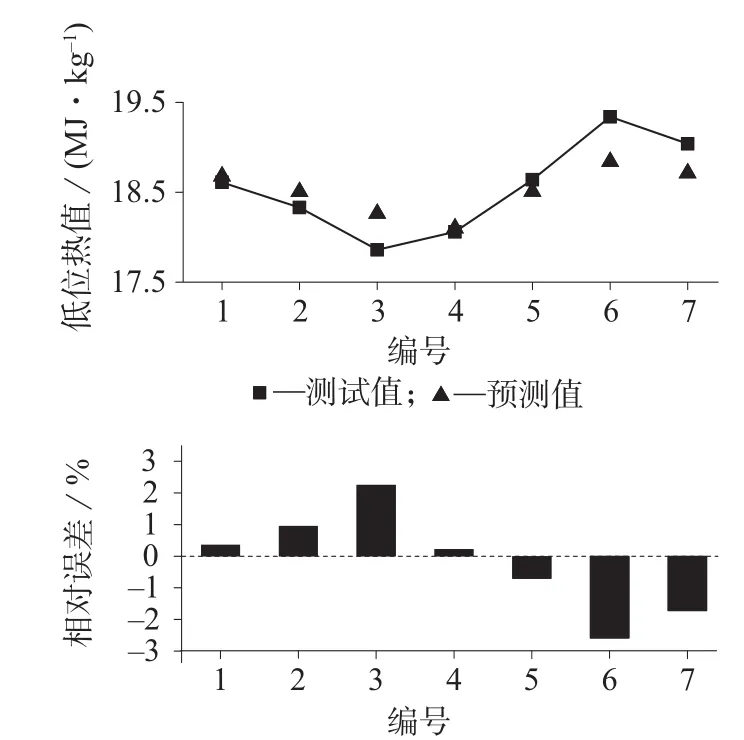
图2 生物质固体燃料高位热值的实测值与预测值对比及相对误差

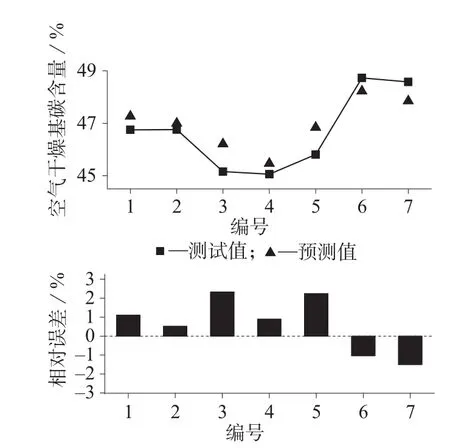
图3 生物质固体燃料空气干燥基碳含量的实测值与预测值对比及相对误差

根据低位热值的MLR模型预测效果分析，由图1可知，预测值与实测值的绝对残差范围为0.04～0.50，相对残差范围为–2.32%～3.05%，由此可见，Ylow多元线性回归方程对低位热值的预测效果较为理想。根据高位热值的MLR模型预测效果分析，由图2可知，预测值与实测值的绝对残差范围为0.04～0.40，相对残差范围为–2.59%～2.26%，误差范围较小，反映了Yhigh多元线性回归方程较好的预测效果。由图3可知，空气干燥基碳含量的MLR模型计算得到的预测值与实验值的绝对残差范围为0.51～1.05，相对残差范围为–1.50%～2.33%，说明YC模型的碳含量的预测结果理想。综上分析，以生物质固体燃料工业分析的4项指标建立的多元线性回归预测模型的预测误差在合理的范围内，并且与其他学者的研究结果相比，误差范围明显减小，证明了MLR多元线性回归方法应用于低位热值、高位热值及碳元素分析指标预测的可行性和实用性。

2.3 模型的应用域

每个模型的应用范围是有一定限度的，即使经过了内部验证和外部验证确认所建模型是稳健、可靠且具有很好的泛化能力和预测能力，但也不能认定该模型能对任何未知样本做出可靠的预测。因此定义模型的应用域是将所建模型应用到未知样本之前的一个重要步骤。本实验模型应用域的定义采用Leverage方法，用Williams图分析生物质固体燃料低位热值、高位热值和空气干燥基碳含量模型的应用域，结果见图4～图6。

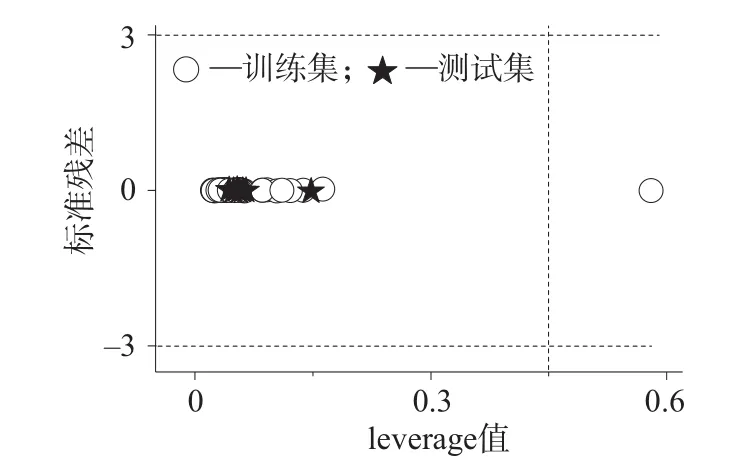
图4 低位热值预测模型的Williams图

图5 高位热值预测模型的Williams图

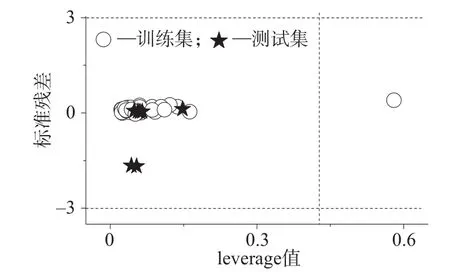
图6 空气干燥基碳含量预测模型的Williams图

根据定义计算得到3个模型的leverage值h* 为0.43。对于生物质固体成型燃料低位热值、高位热值和空气干燥基碳含量这3个模型，由式(4)计算得到第11组训练集样本的h11值为0.58，超出h*。但由于其对应的低位热值、高位热值和碳元素含量的标准残差比较小，由式(5)分别计算得到–0.006，–0.009，0.394，因此可以保留该组样本，不影响模型的稳定性［17］。因此根据图2的分析可知，3个模型的样本均落在应用域范围内，表明模型的预测是准确可靠的。

3 结论

(1)利用秸秆类生物质固体成型燃料的测试数据(工业分析、低位热值、高位热值及碳元素分析指标)，以工业分析中的水分、灰分、挥发分和固定碳含量指标为4个自变量，分别以与上述指标相关性强的低位热值、高位热值和碳元素分析为因变量，通过MLR方法建立了3组多元线性回归预测模型。内部检验和外部检验说明3组模型在应用域范围内均具有理想的预测能力，拟合效果良好，误差范围显著减小。说明通过工业分析指标来预测秸秆类生物质固体成型燃料的热值和碳元素含量是可行实用的。

(2)本研究与已有相关报道相比，构建的预测模型的拟合效果更好，误差范围明显减小，并且对模型应用域的合理性进行了探究。本研究可为秸秆类生物质固体成型燃料理化特性之间的定量关系的探索提供参考，为工业用途的生物质固体成型燃料的热值和元素分析快速做出反映建立起一套便捷简单的计算方法，对生物质固体成型燃料的应用和发展具有重要意义。

(3)本研究的对象为秸秆类生物质固体成型燃料，为了能够促进本研究成果更广泛的应用，将进一步探究包含不同组分如树皮、花生壳、木屑等生物质固体成型燃料的热值和碳元素分析预测模型的建立方法。

［1］马文超，陈冠益，颜蓓蓓，等.生物质燃烧技术综述［J］.生物质化学工程，2007，40(1): 43–48.

［2］魏伟，张绪坤，祝树森，等.生物质能开发利用的概况及展望［J］.农机化研究，2013(3): 7–11.

［3］田宜水，赵立欣，孟海波，等.欧盟固体生物质燃料标准技术进展［J］.可再生能源，2007，25(4): 61–64.

［4］Parikh J，Channiwala S A，Ghosal G K. A correlation for calculating HHV from proximate analysis of solid fuels ［J］. Fuel，2005，84(5): 487–494.

［5］陈文敏.煤质分析结果的定性与定量审查［M］.北京：煤炭工业出版社，1994.

［6］Lei B L，Ma Y M，Li J Z，et al. Prediction of the adsorption capability onto activated carbon of a large data set of chemicals by local lazy regression method ［J］. Atmos Environ，2010，44(25): 2 954–2 960.

［7］汤烨，付殿峥，付正辉，等.木质生物质理化性质指标预测模型建立及应用［J］.电力建设，2013.34(9): 71–75.

［8］Gharagheizi F，Eslamimanesh A，Ilani-Kashkouli P，et al. QSPR molecular approach for representation／prediction of very large vapor pressure dataset ［J］. Chem Eng Sci，2012，76: 99–107.

［9］Dearden J C，Cronin M T D，Kaiser K L E. How not to develop a quantitative structure–activity or structure–property relationship (QSAR／QSPR)［J］. SAR QSAR Environ Res，2009，20(3–4): 241–266.

［10］Roy K，Kabir H. QSPR with extended topochemical atom (ETA) indices: Exploring effects of hydrophobicity，branching and electronic parameters on logCMC values of anionic surfactants ［J］. Chem Eng Sci，2013，87: 141–151.

［11］Wagener M，Sadowski J，Gasteiger J. Autocorrelation of molecular surface properties for modeling corticosteroid binding globulin and cytosolic Ah receptor activity by neural networks ［J］. J Am Chem Soc，1995，117(29): 7 769–7 775.

［12］Mhlanga P，Hassan W A W，Hamerton I，et al. Using combined computational techniques to predict the glass transition temperatures of aromatic polybenzoxazines ［J］. PloS one，2013，8(1): e53367.

［13］Saghaie L，Shahlaei M，Fassihi A，et al. QSAR Analysis for Some Diaryl-substituted Pyrazoles as CCR2 Inhibitors by GA–Stepwise MLR ［J］. Chem Biol Drug Des，2011，77(1): 75–85.

［14］Tropsha A，Gramatica P，Gombar V K. The importance of being earnest: validation is the absolute essential for successful application and interpretation of QSPR models ［J］. Molecular Inform，2003，22(1): 69–77.

［15］Gharagheizi F，Eslamimanesh A，Ilani-Kashkouli P，et al. QSPR molecular approach for representation／prediction of very large vapor pressure dataset ［J］. Chem Eng Sci，2012，76: 99–107.

［16］吴文胜，张灿阳，李秀喜，等.跨尺度方法研究聚合物载药胶束的定量构性关系［J］.化工学报，2015，66(6): 2 303–2 312.

［17］Wu W，Zhang R，Peng S，et al. QSPR between molecular structures of polymers and micellar properties based on block unit autocorrelation (BUA)descriptors ［J］. Chemometr Intell Lab，2016，157: 7–15.

欢迎订阅2016年《计测技术》

《计测技术》创刊于1958年，是中航工业北京长城计量测试技术研究所（国防科技工业第一计量测试研究中心）主办的计量测试技术类期刊，双月刊，逢双月28日出版，国内外公开发行。

《计测技术》是中国核心期刊（遴选）数据库收录期刊，中国学术期刊综合评价数据库统计源期刊，中国期刊全文数据库、中文科技期刊数据库、台湾CEPS期刊数据库全文收录期刊。国际刊号：ISSN 1674-5795，国内刊号：CN 11-5347/ TB。

本刊为国防科技工业系统、部队、民用计量测试院所、高等院校、相关设备制造商和各大公司服务。广泛刊载长、热、力、电、无线电、时间频率、光学、电离辐射、声学等计量测试、校准稿件。设有综合评述，理论与实践，新技术新仪器，计量、测试与校准，计量信息化与管理，经验与体会等主要栏目。

欢迎订阅2016年度杂志，本刊邮发代号：80–441；全年定价：60元。读者可到各地邮局订阅，也可直接与编辑部联系。

通讯地址：北京市海淀区1066信箱杂志社 邮政编码：100095

电话：010-62457159 (编辑部)，010-62457160(广告部)，传真：010-62457159，E-mail: mmt304@126.com

《计测技术》2017年第37卷第2期目次

综合评述

专用测试系统计量校准问题讨论

轴系扭矩测量方法与发展趋势

微压测量和校准技术分析与发展趋势

理论与实践

超音速条件下基于CFD的压力探针校准特性数值模拟

计量、测试与校准

测量系统分析技术在构件钢筋保护层厚度检测中的应用

基于VBA实现黑体辐射源发射率偏离1引起有效亮度温度修正

出租车计价器内部时钟稳定性实验及分析

薄膜热电偶热电特性分析与试验

新技术新仪器

基于半导体制冷片的高精度控温电路系统设计

经验与体会

双活塞式压力计准确度等级的确定

交流标准电阻器技术浅析

Development of Prediction Models for Heating Value and Carbon Content of Biomass Solid Fuel

Guan Ju， Nie Shuyu
(Guangzhou Institute of Energy Testing， Guangzhou 511447， China)

The prediction models for the heating value and carbon content of biomass solid fuel were established. Based on the measured data of straw biomass solid fuel，MLR method was used to establish multiple linear regression forecast models. The industrial analysis of moisture，ash content，volatile and fixed carbon content indexes were secleted as four independent variables，while low heating value，high heating value or carbon content were the dependent variable. The internal and external inspections of the three models demonstrated that all the models had ideal prediction ability and the error range decreased remarkably. TheR2andR2prepvalues of prediction model of high heating value were 0.900 and 0.730，respectively，while the decreased relative residual error range was –2.59% to 2.26%. The research is capable of rapidly reflecting the heating value and elemental analysis of biomass solid fuel for industrial use.

bomass solid fuel; heating value; carbon element; multiple linear regression; prediction model

O651

A

1008–6145(2017)03–0031–06

*广州市质量技术监督局科技项目(2014KJ10)

联系人：聂淑瑜；E-mail: 403692162@qq.com

2017–02–16

10.3969／j.issn.1008–6145.2017.03.007