小型无人直升机航向线性自抗扰控制
丁 力 马 瑞 单文桃 吴洪涛
(1.江苏理工学院机械工程学院, 常州 213001; 2.南洋理工大学机械与宇航工程学院, 新加坡 639798;3.南京航空航天大学机电学院, 南京 210016)
小型无人直升机航向线性自抗扰控制
丁 力1马 瑞2,3单文桃1吴洪涛3
(1.江苏理工学院机械工程学院, 常州 213001; 2.南洋理工大学机械与宇航工程学院, 新加坡 639798;3.南京航空航天大学机电学院, 南京 210016)
针对小型无人直升机航向系统存在内部不确定性和外部扰动大的问题,提出了一种基于线性自抗扰控制(LADRC)算法来实现航向通道高性能控制方法。首先,分析和推导了Trex-600型无人直升机的航向模型,并引入阵风模型模拟实际飞行环境。然后,根据LADRC的控制原理设计了基于二阶LADRC的航向控制系统,并利用人工蜂群算法对控制器参数进行了整定。最后,对所设计的控制策略进行了仿真分析与实验验证,实现了无人直升机航向通道的轨迹跟踪控制,并与常见的PID控制进行了比较。结果表明:设计的LADRC控制器鲁棒性好、响应时间快、控制精度高,能够使Trex-600型无人直升机的航向角快速、精确地跟踪参考轨迹。
小型无人直升机; 线性自抗扰控制; 人工蜂群算法; 参数整定; 轨迹跟踪
引言
随着无人机技术的发展,小型无人直升机在农田作业、城市航拍和电力检测等应用领域受到了国内外学者的广泛关注[1-2]。作为一个多输入多输出的非线性系统,无人直升机易受模型不确定性和外部扰动的影响[3-4],这些因素使飞行控制器设计难度加大。为了提高无人直升机的操控品质,需要研究一种抗干扰能力强的高性能控制器。
航向通道的控制是整个无人直升机控制系统中的关键部分,其不仅是直升机正常飞行的保证,也影响着无人机起飞与降落时的动态性能,故设计合理的航向控制器至关重要[5-6]。针对无人直升机的航向控制,学者们提出了不同的控制方法。例如,BERGERMAN等[7]采用分环控制的方法,即内环设计LQR控制器来配置直升机线性系统的不稳定极点,外环设计PD控制器实现航向稳定控制。RAPTIS等[8]将无人直升机线性系统解耦成2个子模型,并设计PID控制器完成了航向模型的轨迹跟踪控制。在获得Helion无人直升机精确航向模型的基础上,CAI等[9]采用组合非线性反馈控制策略设计了航向控制器,使得航向角速度控制误差维持在31(°)/s左右。值得注意的是,这些控制器设计时都需要精确的飞行动力学模型及相关参数,而实际无人直升机航向系统总是存在着外部不确定性(未知干扰)与内部的动态变化(参数不确定性),这就导致基于精确模型的数学仿真与实飞测试之间总是存在着误差。
针对上述问题,方勇纯等[10]和TANG等[11]利用自抗扰控制(Active disturbance rejection controller,ADRC)的优势完成了航向系统的抗干扰控制,但ADRC结构复杂,控制器参数过多(10个左右),不便于实际工程应用。随后,GAO[12]将ADRC的控制器与扩张观测器均以线性形式表现出来,并提出了线性自抗扰控制(Linear active disturbance rejection controller,LADRC)技术。LADRC继承了ADRC利用误差反馈控制的思想,具有控制参数少、结构简单的特点,更适合实际工程应用。
为减弱由系统内部不确定性与外部扰动带来的影响,本文基于LADRC设计无人直升机航向系统的控制器。然后,采用人工蜂群算法(Artificial bee colony algorithm,ABC)对控制参数进行整定。最后,通过轨迹跟踪仿真和飞行实验对本文所设计航向控制器的有效性进行验证。
1 系统描述
1.1 航向模型
由无人直升机运动学方程可知航向角ψ的数学描述为[13]
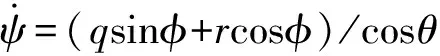
(1)
式中φ、θ——滚转角和俯仰角q、r——俯仰和偏航角速度
当无人直升机处于悬停或平飞状态时,由于滚转角与俯仰角较小,即有φ≈0,θ≈0。因此,式(1)可以改写为
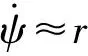
(2)
对于航向通道而言,为了降低航向运动对操作的敏感性,通常会在无人直升机上安装偏航角速率陀螺仪与反馈控制器,故在航向模型中应该考虑偏航角速率反馈控制器的动态特性。根据文献[14],可采用一个等效的一阶系统来描述这个动态特性,即
(3)
式中rfb——偏航角速率反馈系数Kr、Kfb——未知系数
为了便于航向控制器的设计,将式(3)改写成状态空间方程形式,并搭建如图1所示的Trex-600型小型无人直升机系统进行辨识实验,整个系统包含地面站、ACS飞行控制模块、GPS模块、Futaba无线电遥控器、数传等。根据文献[15]提出的PEM-ABC系统辨识方法可以很容易辨识模型中的未知参数,即
(4)
联立式(2)和式(4)可知输入信号uped和航向角ψ是二阶导关系,所以Trex-600型无人直升机的航向模型是一个二阶系统。

图1 Trex-600型小型无人直升机系统Fig.1 Trex-600 small-scale unmanned helicopter system
1.2 阵风模型
为了更真实地模拟无人直升机的飞行环境,在航向模型中嵌入阵风模型。阵风模型可由Gauss-Markov方程生成[16]。
(5)
式中dw——垂直方向的风扰速度向量qw——零均值噪声信号B——干扰输入项ρ*——权重因子τs——与风速相关的时间常数
本文取垂直方向风速为6 m/s,τs为3.2,ρ*为0.5。
2 基于LADRC的航向控制器设计
LADRC是一种对模型依赖程度不高的控制算法,可通过线性扩张观测器(Linear extended state observer,LESO)观测出系统的外部扰动及非线性动态特性的变化来实现闭环系统的实时估计与补偿控制,尤其适合无人直升机这类高阶、强耦合、欠驱动的非线性系统。
以二阶系统为被控对象
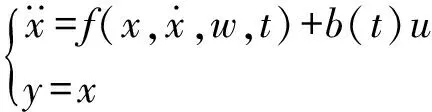
(6)

(7)
式中b0为b(t)的近似值,则
(8)
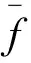
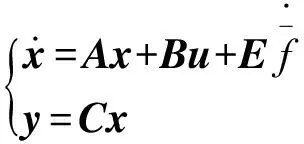
(9)
其中
x=[x1x2x3]T

采用LESO对式(9)进行观测,即
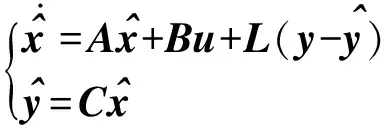
(10)
其中
=[123]T
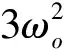
选择控制律为u=(-+u0)/b0,则二阶系统的控制可转换为简单的积分控制形式即
(11)
式中re——参考输入信号k1、k2——比例系数
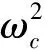
根据二阶LADRC控制器的原理设计无人直升机航向控制系统,如图2所示。ψr为航向通道的参考信号,只需要调整ωo、ωc和b0的值,就可以保证整个航向系统BIBO稳定。

图2 基于LADRC的航向控制系统Fig.2 Yaw control system based on LADRC
3 参数整定
参数整定是LADRC控制器设计的关键性问题之一。如图3所示,本文采用ABC算法来寻找最优的控制器参数,算法具体步骤可参照文献[18],本文不再赘述。给定ψr为0.2 rad的阶跃信号为参考值,并添加平均风速为0.1 m/s的阵风干扰和强度为0.001 dB的高斯白噪声作为总扰动,设定优化目标函数F为
(12)
式中α、ε、β、σ——调节参数ts——调节时间os——超调量
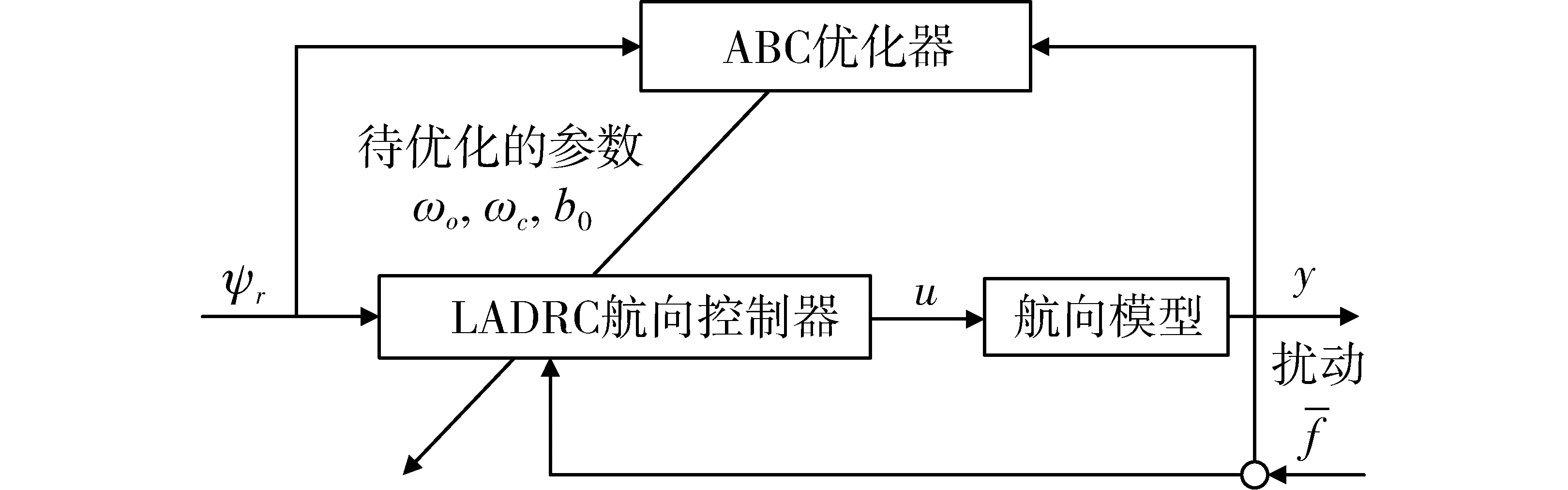
图3 基于ABC算法的参数整定Fig.3 Parameters tuning based on ABC algorithm
设置ABC算法的参数为:种群数为20,搜索阈值为5。为进行对比分析,笔者同时采用遗传算法(Genetic algorithm,GA)和粒子群算法(Particle swarm optimization,PSO)来完成航向控制器的参数整定,相应的算法参数设置为:抗体个数为20,交叉因子为0.8,变异因子为0.2;粒子总数为20,学习因子为2,权重因子为0.5。3种算法的最大迭代次数均为50,各运行10次,取最好的优化结果,并记录下该次迭代过程中每代最优目标函数值,如图4所示。从图中可以看出,ABC算法在20代左右便开始收敛,而GA算法与PSO算法分别在28代和26代才开始收敛,且3种算法获得的最优目标函数值分别为0.931 2、1.037 4和1.017 8。在收敛速度上,本文算法比其他2种算法分别快了40%和30%;在求解质量上,本文算法比其他2种算法分别提高了11.4%和9.3%。经ABC算法整定后的参数为:b0=45,ωo=68,ωc=21。
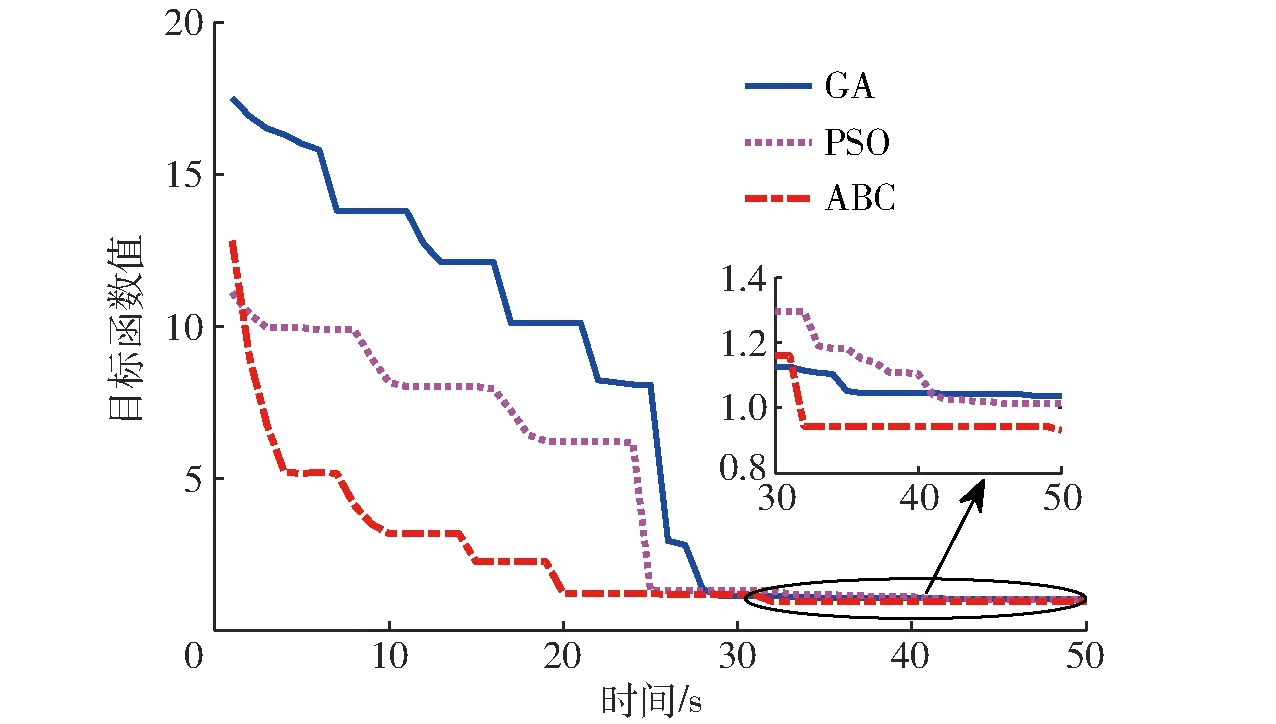
图4 3种算法的迭代曲线Fig.4 Iteration curves regarding three algorithms

图6 2种控制器下的轨迹跟踪对比Fig.6 Comparisons of trajectory tracking for two controllers
由图5航向角的响应曲线可见,3种算法优化下的无人直升机航向角都能够较好地跟踪上参考指令信号。虽然,经ABC算法整定的航向角在响应速度上要略慢于PSO算法,但在稳定时间上快于其他2种算法。这说明本文所提算法能够充分开发被搜索对象的信息,具有较强的全局搜索能力。
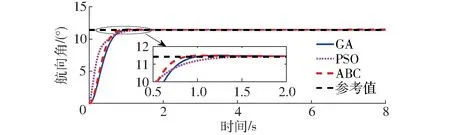
图5 3种算法优化下航向角的阶跃响应Fig.5 Step response of yaw regarding three algorithms
4 仿真分析与实验验证
4.1 轨迹跟踪仿真
为了验证本文所设计控制器的性能,分别采用LADRC控制和PID控制算法对无人直升机航向系统进行抗干扰轨迹跟踪仿真。在仿真中添加和第3节一样的总扰动,并利用Cycloidal曲线[19]生成参考轨迹
(13)
式中Si——初始轨迹Stotal——轨迹总长度Te——生成轨迹的时间
在本次算例中,设置参考轨迹初始值零,4 s时,开始上升至0.261 8 rad,7 s时,开始回降至零,仿真时间共持续8 s。
2种控制算法均通过ABC算法进行参数整定,PID控制参数的整定过程可参照文献[20]。经整定后,LADRC的控制参数为:b0=40,ωo=97,ωc=24;PID的控制参数为:KP=100,KI=3.5,KD=15。
图6给出了通过2种控制算法得到的仿真结果。图6a为参考信号经2种控制策略生成的航向控制输入信号,与PID控制器相比,LADRC控制器基本上能够抑制住系统扰动;由图6b可见,前4 s内由LADRC控制器获得的偏航角速度r波动较小,稳态误差基本保持在±0.03 rad/s内,而采用PID控制器,r的稳态误差只能保持在±0.1 rad/s内,这说明LADRC具有更高的控制精度;由图6c可见,虽然2种控制算法都能使无人直升机航向角跟踪参考轨迹,但由LADRC控制器产生的跟踪效果更佳。
(14)
(15)
式中l(i)——第i采样时刻参考航向角与仿真航向角的偏差
N——总采样数
表1为2种控制策略在航向角跟踪上的误差,结果显示由LADRC产生的最大跟踪误差和均方差均小于由PID产生的。这说明LADRC具有更强的鲁棒性与适应性。
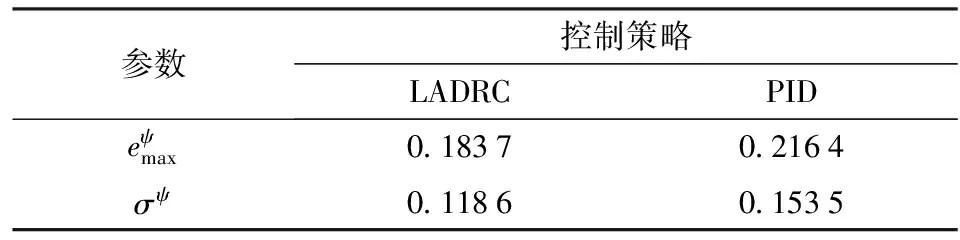
表1 航向角跟踪误差对比Tab.1 Comparison of trajectory tracking error of yaw rad
4.2 轨迹跟踪实验
为了进一步验证LADRC控制算法的实用性,本文在Trex-600型无人直升机系统上进行航向角的轨迹跟踪实验,如图7所示。另外,表2给出了ACS飞行控制模块的关键指标,相关参数表明ACS可以测量常规无人直升机航向角的数据。在仿真获得LADRC控制器参数的基础上,通过Matlab代码转化功能将LADRC控制算法转换为C代码,并写入ACS飞行控制模块中。飞行实验中,飞行手先将直升机飞至悬停状态,再把航向通道切换到自由飞行状态,使直升机仅依靠LADRC控制器自主跟踪方波信号,并利用地面站记录下实验结果。选取飞行历史中的某10 s实验段进行分析,如图8所示。
从图中可以看出,系统的航向输出基本上能够跟踪上参考信号,稳态时的跟踪误差不超过±2.86°。因此,本文所设计的控制系统可实现无人直升机航向角的高精度轨迹跟踪控制。

图7 Trex-600型无人直升机航向轨迹跟踪实验Fig.7 Yaw angle trajectory tracking test of Trex-600 unmanned helicopter

表2 ACS飞行控制模块的关键指标Tab.2 Specifications of ACS flight control module
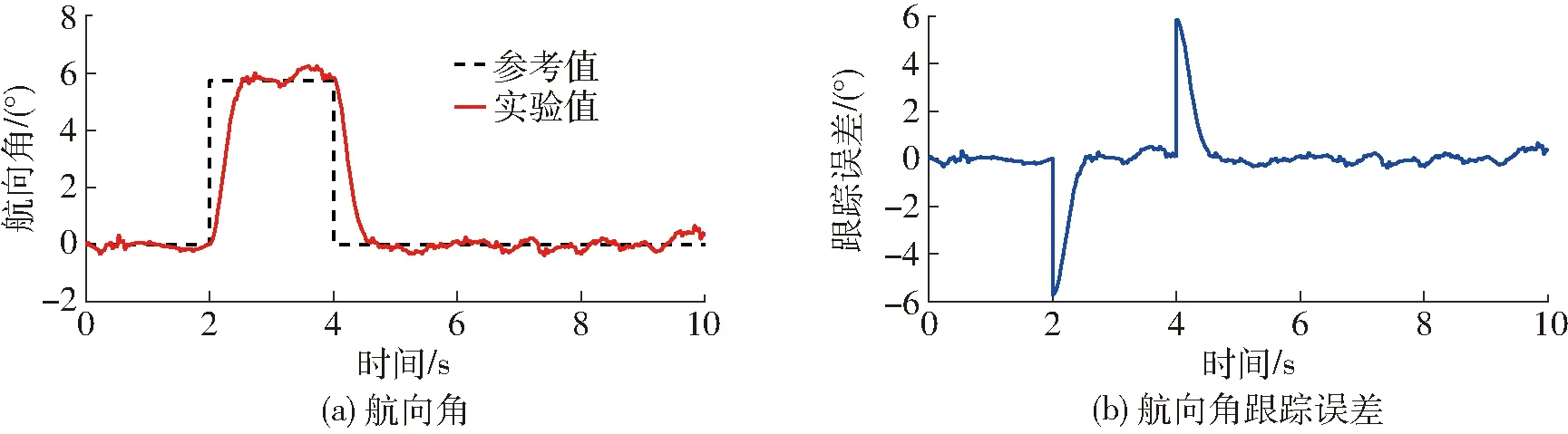
图8 航向角轨迹跟踪实验结果Fig.8 Experiment results of yaw angle trajectory tracking
5 结论
(1)根据小型无人直升机航向系统的动态特性,建立了航向通道的数学模型。搭建Trex-600型无人直升机系统,利用PEM-ABC算法辨识出了航向模型的未知参数。通过基于LADRC的控制系统实现了航向角的轨迹跟踪仿真,获得了较好的效果,进一步证明了辨识算法的有效性。
(2)利用ABC算法对LADRC控制器参数进行了整定,并与GA算法、PSO算法进行对比,结果表明ABC算法无论在收敛速度上还是求解质量上都要优于其他2种算法,更适合解决参数整定问题。
(3)相比基于PID的无人直升机航向控制器,本文设计的LADRC控制器具有控制精度高、响应速度快、鲁棒性强、适应性好的优点,能够更有效抑制系统扰动。
(4)通过Trex-600型无人直升机系统进行了航向角的跟踪实验,结果表明基于LADRC的稳态跟踪误差在±2.86°范围内。这进一步验证了LADRC控制器设计和轨迹跟踪仿真的有效性。
1 GANDOLFO D C, SALINAS L R, BRANDO A S, et al. Path following for unmanned helicopter: an approach on energy autonomy improvement[J]. Information Technology and Control, 2016, 45(1): 86-98.
2 ALVARENGA J, VITZILAIOS N I, VALAVANIS K P, et al. Survey of unmanned helicopter model-based navigation and control techniques[J]. Journal of Intelligent & Robotic Systems, 2015, 80(1): 87-138.
3 CHOI Y H, YOO S J. A simple fuzzy-approximation-based adaptive control of uncertain unmanned helicopters[J]. International Journal of Control, Automation and Systems, 2016, 14(1): 340-349.
4 RAZZAGHIAN A, MOGHADDAM R K. Adaptive fuzzy sliding mode control for a model-scaled unmanned helicopter[J]. Journal of Fuzzy Set Valued Analysis, 2016, 2016(3): 286-302.
5 SHENG S, SUN C. Yaw control of an unmanned helicopter using adaptive model feedback and error compensation[J]. Journal of Aerospace Engineering, 2015, 29(2): 06015002.
6 ZHOU J, KHOT L R, PETERS T, et al. Efficacy of unmanned helicopter in rainwater removal from cherry canopies[J]. Computers and Electronics in Agriculture, 2016, 124: 161-167.
7 BERGERMAN M, AMIDI O, MILLER J R, et al. Cascaded position and heading control of a robotic helicopter[C]∥2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, 2007: 135-140.
8 RAPTIS I A, VALAVANIS K P. Linear and nonlinear control of small-scale unmanned helicopters[M]. Berlin: Springer Science & Business Media, 2010: 73-102.
9 CAI G W, CHEN B M, PENG K, et al. Modeling and control of the yaw channel of a UAV helicopter[J]. IEEE Transactions on Industrial Electronics, 2008, 55(9): 3426-3434.
10 方勇纯, 申辉, 孙秀云, 等. 无人直升机航向自抗扰控制[J]. 控制理论与应用, 2014, 31(2): 238-243. FANG Y C, SHEN H, SUN X Y, et al. Active disturbance rejection control for heading of unmanned helicopter[J]. Control Theory & Applications, 2014, 31(2): 238-243.(in Chinese)
11 TANG S, YANG Q H, QIAN S K, et al. Height and attitude active disturbance rejection controller design of a small-scale helicopter[J]. Science China Information Sciences, 2015, 58(3): 1-17.
12 GAO Z Q. Active disturbance rejection control: a paradigm shift in feedback control system design[C]∥2006 American Control Conference, 2006: 2399-2405.
13 ALVARENGA J, VITZILAIOS N I, VALAVANIS K P, et al. Survey of unmanned helicopter model-based navigation and control techniques[J]. Journal of Intelligent & Robotic Systems, 2015, 80(1): 87-138.
14 DING L, WU H T, YAO Y. Chaotic artificial bee colony algorithm for system identification of a small-scale unmanned helicopter[J]. International Journal of Aerospace Engineering, 2015, 2015: article ID801874.
15 丁力, 吴洪涛, 姚裕, 等. 基于PEM-ABC算法的小型无人直升机系统辨识[J/OL]. 农业机械学报, 2016, 47(1): 8-14. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?file_no=20160102&flag=1. DOI:10.6041/j.issn.1000-1298.2016.01.002. DING L, WU H T, YAO Y, et al. Hybrid PEM-ABC algorithm for system identification of a small-scale unmanned helicopter[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(1): 8-14. (in Chinese)
16 GADEWADIKAR J, LEWIS F L, SUBBARAO K, et al. H-infinity static output-feedback control for rotorcraft[J]. Journal of Intelligent and Robotic Systems, 2009, 54(4): 629-646.
17 GAO Z. Scaling and bandwidth-parameterization based controller tuning[C]∥Proceedings of the American Control Conference, 2006: 4989-4996.
18 SUN C H, DUAN H B. Artificial bee colony optimized controller for unmanned rotorcraft pendulum[J]. Aircraft Engineering and Aerospace Technology, 2013, 85(2): 104-114.
19 BONE G M, XUE M, FLETT J. Position control of hybrid pneumatic-electric actuators using discrete-valued model-predictive control[J]. Mechatronics, 2015, 25: 1-10.
20 ABACHIZADEH M, YAZDI M R H, YOUSEFI-KOMA A. Optimal tuning of pid controllers using artificial bee colony algorithm[C]∥2010 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, 2010: 379-384.
Linear Active Disturbance Rejection Control for Yaw Channel of Small-scale Unmanned Helicopter
DING Li1MA Rui2,3SHAN Wentao1WU Hongtao3
(1.CollegeofMechanicalEngineering,JiangsuUniversityofTechnology,Changzhou213001,China2.SchoolofMechanical&AerospaceEngineering,NanyangTechnologicalUniversity,Singapore639798,Singapore3.CollegeofMechanicalandElectricalEngineering,NanjingUniversityofAeronauticsandAstronautics,Nanjing210016,China)
Small-scale unmanned helicopter has a peculiar flight feature of vertically take-off and landing, fixed position hovering, flying in low velocity, forward flight, rearward flight and so on. It is mainly used for civilian and military field with the advantage of light weight, low price and small scale. However, the small-scale unmanned helicopter is a strong coupled, under actuated, multivariable, time varying, open-loop unstable and high order nonlinear system. It is a great challenge to realize the research of its autonomous flight. Aiming at the internal uncertainties and large disturbance of the small-scale unmanned helicopter, a controller for yaw channel based on linear active disturbance rejection controller (LADRC) was proposed to realize the high performance control. Firstly, the yaw model of Trex-600 unmanned helicopter was analyzed and deduced, and the gust model was introduced to simulate the actual flight environment. Then, the principle of LADRC was elaborated and the yaw control system was designed based on LADRC of second order. In order to obtain the appropriate control parameters, the novel artificial bee colony algorithm was applied to conduct parameters tuning. Lastly, a trajectory tracking simulation and experiment were used to test the proposed controller compared with the PID controller. The results showed that the LADRC controller had the ability of good robustness, fast response and high control precision. The yaw angle of the Trex-600 unmanned helicopter can track the referenced trajectory fleetly and accurately.
small-scale unmanned helicopter; linear active disturbance rejection control; artificial bee colony algorithm; parameters tuning; trajectory tracking
2016-08-25
2016-10-07
国家自然科学基金青年基金项目(51405209)
丁力(1989—),男,讲师,博士,主要从事无人直升机动力学建模与控制和智能算法研究,E-mail: nuaadli@163.com
10.6041/j.issn.1000-1298.2017.05.002
TP273; V279+.2
A
1000-1298(2017)05-0022-06

