基于均值预估的协同过滤推荐算法改进

蒋宗礼，王 威，陆 晨

(北京工业大学 计算机学院，北京 100124)

基于均值预估的协同过滤推荐算法改进

蒋宗礼，王 威，陆 晨

(北京工业大学 计算机学院，北京 100124)

在协同过滤推荐系统中，用户-项目矩阵中存在大量未评分元素，且最终预测值由“最近邻”用户所评分数的加权平均产生。传统算法将未评分元素直接计作0，导致预测得分普遍偏低。针对这种稀疏性引起的问题，提出了一种基于均值预估的协同过滤改进算法。该算法以“最近邻”用户所给平均值对未评分的数据进行估计，有效降低了未评分项目所带来的负面影响。同时该方法又不是单纯的平均值填充，而是在协同过滤算法的第三阶段，需要用到“最近邻”用户对预测项目的评分时，才对“最近邻”评分为0的分值进行替代，这样不会影响到计算的相似度，预测结果不至于平庸。稀疏度为93.7%的数据上的实验表明，在不影响相似度计算的前提下，改进算法可显著降低均方根误差，提高推荐质量；最佳RMSE值可达1.01。

协同过滤；推荐算法；稀疏性；评分预测；均方根误差

0 引 言

随着互联网2.0的快速发展，信息过载成为了人们遇到的一个问题，怎样帮助用户从海量信息中发现自身感兴趣的内容变得至关重要，推荐系统由此应运而生[1]。目前，推荐系统已经有一些方法，包括基于内容的方法、协同过滤方法和混合推荐方法。其中协同过滤方法是推荐系统中最基本的方法[2]，该方法又分为基于用户的协同过滤(User-based)和基于项目的协同过滤(Item-based)[3-4]。

协同过滤方法通过用户行为建立兴趣模型，根据邻居集的行为预测当前用户。因此，在相应的用户-项目矩阵中用户评分项目越多，推荐质量就越高，但随着用户项目的不断增多，用户-项目矩阵就越来越稀疏[5-7]，这对推荐结果的改善提出了较大挑战。将一个用户的邻居用户中距离该用户比较近的称为近邻用户，简称近邻，称最近的K个近邻为“K近邻”。

针对上述问题，对协同过滤算法进行了改进。对某个用户，当出现未评分项的情况时，用该项的最近邻评分均值进行预测替代，其代价是需要维护一个用户评分平均值矩阵，而不需要更多地增加算法的时间复杂性。在MovieLens上的实验结果表明，新算法的计算效能有了很大提高。

1 基本协同过滤推荐算法讨论

1.1 评分预测方法

协同过滤算法根据邻居的行为数据对目标用户产生评分预测或者推荐列表，算法流程分为三个步骤[8]：

(1)利用用户的评分数据计算用户或者项目之间的相似程度；

(2)选定K值，为每个用户寻找K近邻用户；

(3)利用最近邻的评分数据预测用户对未知项目的评分。

第三步评分预测产生推荐结果。传统的评分预测方法主要有三种[9-10]。

以基于用户的协同过滤为例。对于用户u，最简单的方法是直接使用邻居集合中的K个用户对未知项目i的平均打分来得到预测值Pu,i，如式(1)所示。

(1)

其中，N(u)为u的K近邻用户集合；Rv,i为用户v对项目i的评分。

该方法是把集合中的邻居用户同等对待，虽然简单，但会降低预测结果的个性化程度。事实上，每个邻居用户与目标用户的相关性是不一样的，他们对目标用户的评分影响贡献也应该是不一样的。

一种改进方法是把邻居用户与目标用户的相似度作为权值，与邻居用户的评分进行加权求和，给出预测用户对项目i的评分。该方法能反映出不同用户所做出的贡献。

一般用式(2)计算相应的Pu,i：

(2)

其中，Sim(u,v)表示用户u和用户v的相似度。

式(2)虽然使用了用户的加权平均值，但没有考虑不同用户的评分尺度。进一步的改进是加入不同用户更多的个性化因素，充分考虑每个用户的个性评分尺度，以消除个性化所带来的负面影响，通常具有更好的准确度。具体用式(3)计算。

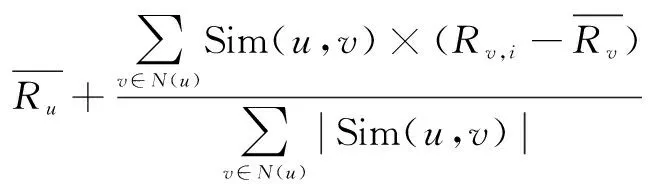
(3)

1.2 评分预测分析

从上述三种评分预测方法中可以看出，预测用户评分需要用到最近邻的评分数据。但由于数据稀疏性，用户的最近邻中存在着大量的未评分元素，由于这些未评分项被简单地置为0，导致了较大误差积累的连锁影响，使得最终推荐结果普遍不理想。究其原因，在这个评价体系中，0表示的是用户对相应的项目不喜欢。事实上，用户对某个项目没有评分，是由于用户对该项目没有行为，而并不一定是不喜欢。因为至少存在着诸如已经获得有关信息、还发现了其他相关信息、时间不允许等导致他不评价的原因。而且这种影响会在算法中出现连锁反映。

例如，简单考虑这样的情景：用户A对项目a，c都打4分，用户B对项目a打了4分，用户C对项目b打了3分。预测一下用户A对项目b的打分情况。

首先，构建用户-项目评分矩阵，如表1所示。

表1 用户-项目评分矩阵

然后找到和用户A相似的邻居B，通过B对项目b的打分预测用户A对项目b的打分，最后求得A对b的打分为0。显然存在：用户B对项目b打分为0不一定代表用户B不喜欢项目b，很可能仅仅是他没有对项目b有过行为。事实上，用户B很不活跃的可能性很大。所以，这种连锁反应使得算法未能够更好地利用K个近邻的相关性，对相关项目进行估计。

综上，三种评分预测方案都未能很好地解决用户邻居未评分的情况，不能有效地近似用户对项目的真实评分，导致推荐质量很不理想。一般来说，可以忽略那些未对项目i评分的最近邻用户(比如l个，用其余的k-l个最近邻用户计算评分[2])。记这种方法为协同过滤的修正算法。在式(2)的基础上设计如下修正方案：

(4)

其中，Sim(u,v)表示用户u和用户v的相似度；NULL表示不考虑未对项目i评分的近邻用户影响，实验中直接忽略，不纳入预测值Pu,i的计算。

2 协同过滤推荐算法的改进

针对基本的协同过滤推荐算法在预测评分时不能有效解决近邻用户的大量未评分数据这一问题，有两种解决途径。第一种是通过机器学习方法做分类，采用隐语义模型和矩阵分解模型进行降维，它需要构造负样本，这种方案效果很好，但负样本的采样一直没有得到令人满意的优化解决，计算代价很大，在实际应用中操作性和实时性不高。第二种是填充缺失值，基于领域进行推荐[2,11-13]。文中利用用户对项目兴趣度的相关性，使用用户本身的平均评分进行预测的方案。该方案不会影响用户-项目矩阵中的未评分元素，只是在最后预测评分时对未评分的数据进行替代。它的好处是不需要填充原始用户-项目矩阵，也就不会影响到用户之间或者项目之间的相似度计算，其代价是需要维护一张用户评分平均值表。

下面基于用户的协同过滤对改进算法进行具体讨论。这里将协同过滤推荐算法划分为三个部分：数据表示、最近邻构建、结果产生。

2.1 数据表示

用户对项目评分可以用表2所示的矩阵R(m,n)来表示，其中m表示用户数，n表示项目数，Rv,i表示用户v对项目i的评分。评分值可以用0、1来表示。Rv,i=1表示用户v喜欢项目i；Rv,i=0表示用户v不喜欢项目i；也可以用一个区间来表达一种喜爱程度。例如，MovieLens中用0～5的整数来表明用户对电影的喜爱程度。以此为基础，对矩阵中没有评分的值进行预测。

表2 数据表示

2.2K近邻形成

在基于用户的协同过滤算法中关键是维护一张用户相似表，它要求对于某一个用户u，需要能够找到他的K近邻用户。定义N(u)={u1,u2,…,uk}表示用户u的近邻用户集序列，序列N(u)中的元素ui根据其与用户u之间的相似程度由大到小排列。相似度的计算方法很多，在基于用户的相似度计算中一般采用向量模型，即把矩阵中的一行看成是用户的特征描述，再用向量模型进行相似度计算。

一般地，相似度的度量方法有三种。

(1)余弦相似度。

把用户对项目的评分组成一个n维向量，并把它看成用户的特征向量(FeatureVector)，通过计算特征向量之间的夹角余弦来度量两个用户之间的相似性，夹角越小说明用户的相似性越大，如式(5)所示。

(5)

其中，I表示用户u和v共同的评分项目集合；Ru,i表示用户u对项目i的评分；Iu和Iv表示用户u和v已经评过分的项目集合。

(2)皮尔逊系数。

皮尔逊系数更加重视用户之间的公共评分项目，其核心思想也是余弦定理。

Sim(u,v)=

(6)

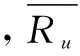
(3)修正余弦相似度。

在余弦相似度的计算过程中，无法考虑不同用户对项目集合评分在尺度上的差异性，有的用户可能总体评分偏高，有的可能总体评分偏低，在这种情况下会出现喜爱程度一样，但评分不一样的状况。由此，可以利用修正的余弦相似度评价来对上述公式进行优化，如式(7)所示。

Sim(u,v)=

(7)

从式(7)中可以看出，修正余弦与皮尔逊相关系数不同点是后者在分母方面采用的是用户共同评分集合，而修正余弦则是单方面用户的评分。

Sarwar利用MovieLens最小数据集对三种方案进行对比，用MAE作为评测指标说明利用修正后的余弦相似度可以获得最优MAE[3]。文中相似度计算方法均采用修正余弦的度量方法。

把得到的结果存放在相似度表中，记为矩阵S(m,m)，其中S(u,v)表示用户u和用户v的相似度。最后根据K值把S(m,m)中用户u对应行中K个最大相似的元素放入用户u的K近邻集合中，构成N(u)。

2.3 评分预测

在得到用户的K近邻后，就可以对未知评分进行预测了。采用改进后的算法对三种方案进行改进。

(1)最简单平均值预测方案改进。

取：

(8)

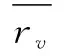
(2)面向相似性的邻居评分加权平均数方案改进。

取：

(9)

其中，Sim(u,v)表示用户u和用户v的相似度。

(3)基于每个用户评分尺度的准确评分公式改进。

取：

(10)

从三种改进方案可以看出，它们的核心是用邻居用户的平均分对打分为0的项目进行替代。

通过实验发现，三种方案各有利弊。第一种方案最简单，它同等看待所有邻居用户的贡献，改进后会使得预测值更加平庸，个性化程度不明显，推荐效果也最差。后两种方法中由于已经采用了修正余弦相似度获得项目的相似度，考虑了不同用户的评分尺度，所以文中直接采用较简单的式(2)及其对应的修正式(4)与改进式(9)对结果进行预测，并对比推荐质量。

3 实 验

3.1 数据集

采用美国明尼苏达GroupLens研究组提供的MovieLens数据集，MovieLens是一个基于推荐算法研究的Web站点[13]，用来接收用户对电影的评分和提供电影推荐列表。现在MovieLens数据集总共分为3个不同大小的版本，文中选用小版本的数据集。它包含了943个用户对1 682部电影的100 000条评分信息，每个用户至少有20条以上的评分信息，评分取值从1到5代表用户的喜好程度。

定义稀疏度为用户未评分条目数占矩阵中所有数据条目的百分比。实验中稀疏度为：

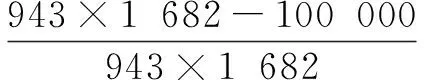
(11)

将数据集分为训练集与测试集，为此引入变量x，表示训练集占数据集的百分比，在实验中始终使x=0.8，即训练集占80%，测试集占20%。另外为了保证评测指标并不是过拟合的，共进行了5次实验，每次实验都使x=0.8，而训练集和测试集都重新随机生成，保证得到不一样的训练集与测试集，最后用5次实验的平均值作为最后的评测指标。

3.2 度量指标

在评分预测中，一般可通过均方根误差(RMSE)和平均绝对误差(MAE)来计算预测准确度[14-15]。

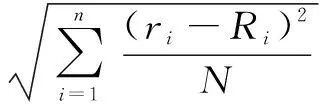
(12)

(13)

其中，Ri为算法的预测评分；ri为真实评分。

其中RMSE是Netflix衡量协同过滤算法的评估指标[2,11]。同时比较式(11)和式(12)可知，RMSE加大了对预测不准的用户项目评分的惩罚(平方惩罚)，因而对推荐算法更加严苛。所以文中选用RMSE作为最终的评测指标。

3.3 实验结果

在MovieLens数据集上离线实验了两种协同过滤推荐算法和它们对应的改进算法，并采用不同K值(10,20,30,40,50,80)对比推荐质量。

表3给出了K值为10时的部分实验结果。

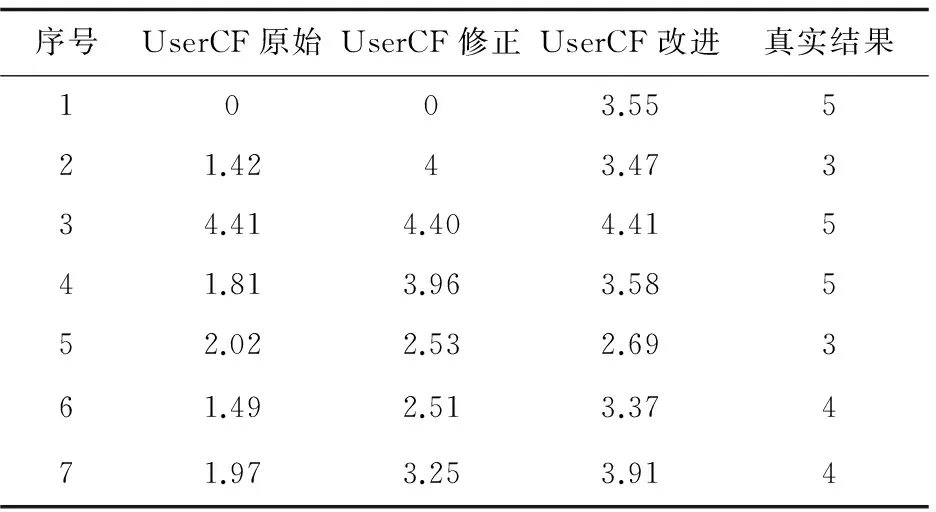
表3 部分实验数据比较

从中可以发现，采用式(4)的修正算法可以对原始结果进行合理的改进，但效果有限，同时修正方案也存在预测评分为0的情况。而改进算法相比前两者能够大幅度地提高预测评分的准确性。

分析式(9)可以推测，使用邻居用户平均分进行替代，预测结果的起伏不会很大，所以最终的预测结果大部分集中在2～5。在实际应用中，用户对项目的打分也是如此，大部分人对自己没有行为的项目或者不是特别喜欢的项目会保守地以中间值附近的分数进行评分，这种结果符合大众的评分心理。

综上所述，改进算法可以更加准确地体现用户现实的状态，预测用户的评分数据，预测结果更加趋近于真实结果，同时也不会过度平庸，仍然能够反映用户的个性化打分。最终结果的RMSE值对比由图1～图3分别给出。

图1 协同过滤推荐结果

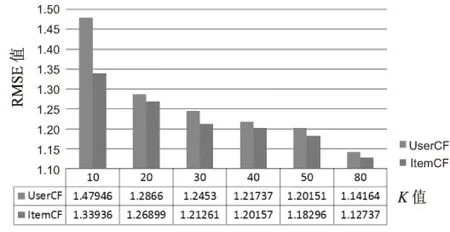
图2 协同过滤的修正推荐结果

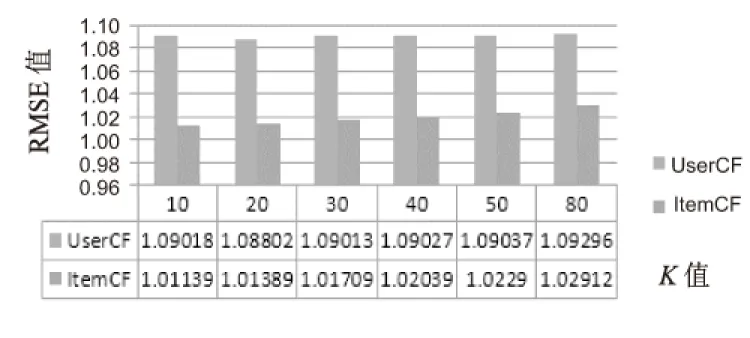
图3 协同过滤的改进推荐结果

对比推荐结果可以看出，修正算法能够提高推荐质量。而经过改进后的算法优于前两种方法，不管是在基于用户的协同过滤，还是在基于项目的协同过滤上，都能够显著提高推荐质量，得到更小的RMSE值。

3.4 分析与讨论

修正算法在评分时忽略了用户对项目评分为0的情况，可以提高推荐质量。但是，这种方法忽略了部分近邻用户，难以更准确地体现用户喜好。由图2可知，当K值较小时，RMSE值不理想，同时，预测的用户评分中仍然存在分数为0的情况(K近邻用户都未对该项目打分)，这是不合理的。而文中改进算法可以有效避免修正算法的弊端，RMSE值下降了0.2左右。

在解决稀疏性的问题中，机器学习途径的核心思想是构造负样本，通过降维的方法补全评分矩阵，一些著名算法在NetflixPrize上的推荐质量很高。例如，在Funk-SVD模型基础上加入偏置项后的BiasSVD模型，在参数F取96时，能将RMSE值降到0.903 9。加入时间信息的TimeSVD++模型在参数F取50时，RMSE值为0.882 4[2]。但这类方法的计算复杂度较高，一些模型只能运用在几百个用户、几百个项目的实验上，在实际运用中实时性很难保证。相比之下，文中提出的改进算法在推荐质量和算法复杂度上都达到了可接受的程度，空间上只需要维护一张用户评分均值表，比机器学习的方法更加易于操作和实用。

4 结束语

针对协同过滤系统中的数据稀疏问题，在预测评分阶段以最近邻用户打分的平均值对未评分的数据进行替代，可以有效降低数据稀疏带来的负面影响，同时又不会影响到用户间的相似度计算，推荐结果不会过度拟合和过度平庸，能更加真实地反映用户的喜好程度，并且该方案比机器学习更加易于操作和实用。实验结果表明，改进算法能够有效避免传统评分预测阶段的弊端，显著提高了推荐算法的推荐质量。最终取得了最好的RMSE值(1.01)。

[1]DeshpandeM,KarypisG.Item-basedtop-nrecommendationalgorithms[J].ACMTransactionsonInformationSystems,2004,22(1):143-177.

[2] 项 亮,陈 义,王 益.推荐系统实践[M].北京:人民邮电出版社,2012.

[3]SarwarB,KarypisG,KonstanJ,etal.Item-basedcollaborativefilteringrecommendationalgorithms[C]//Proceedingsofthe10thinternationalconferenceonworldwideweb.[s.l.]:ACM,2001:285-295.

[4] 蒋宗礼,陆 晨.基于级联二部图的动态推荐算法[J].计算机工程与设计,2013,34(12):4356-4361.

[5] 马宏伟,张光卫,李 鹏.协同过滤推荐算法综述[J].小型微型计算机系统,2009,30(7):1282-1288.

[6] 许海玲,吴 潇,李晓东,等.互联网推荐系统比较研究[J].软件学报,2009,20(2)：350-362.

[7] 冷亚军,陆 青,梁昌勇.协同过滤推荐技术综述[J].模式识别与人工智能,2014,27(8):720-734.

[8]RicciF,ShapiraB.Recommendersystemshandbook[M].[s.l.]:Springer,2011.

[9]ZhongZ,SunY,WangY,etal.Animprovedcollaborativefilteringrecommendationalgorithmnotbasedonitemrating[C]//14thinternationalconferenceoncognitiveinformatics&cognitivecomputing.[s.l.]:IEEE,2015:230-233.

[10] 邓爱林,朱扬勇,施伯乐.基于项目评分预测的协同过滤推荐算法[J].软件学报,2003,14(9):1621-1628.

[11]PanR,ZhouY,CaoB,etal.One-classcollaborativefiltering[C]//EighthIEEEinternationalconferenceondatamining.[s.l.]:IEEE,2008:502-511.

[12] 王元涛.Netflix数据集上的协同过滤算法[D].北京:清华大学,2009.

[13]SchaferJB,DanF,HerlockerJ,etal.Collaborativefilteringrecommendersystems[C]//Theadaptiveweb,methodsandstrategiesofwebpersonalization.[s.l.]:[s.n.],2015:45-46.

[14] 朱郁筱,吕琳媛.推荐系统评价指标综述[J].电子科技大学学报,2012,41(2)：163-175.

[15] 朱扬勇,孙 靖.推荐系统研究进展[J].计算机科学与检索,2015,9(5):513-525.

Improvement of Collaborative Filtering Recommendation Algorithm with Mean Value Estimation

JIANG Zong-li，WANG Wei，LU Chen

(College of Computer Science and Technology,Beijing University of Technology,Beijing 100124,China)

There are a lot of unrated elements in the user-item matrix in collaborative filtering recommendation system,and final prediction value is calculated by the weighted average of nearest-neighbor scores.The values of unrated elements are regarded as 0 by traditional methods,which results in a generally low prediction score for the unrated elements.In order to solve the problem caused by sparsity,an improved collaborative filtering recommendation algorithm with mean value estimation is proposed.The average score of the nearest-neighbor scores are employed to evaluate the unrated data,effective reduction of negative influence of unrated items in this algorithm.At the same time,this method is not a simple average filling,but in the third stage of collaborative filtering algorithm,when needing to use nearest-neighbor users to predict,the 0 score is replaced.This won’t affect the calculation of similarity,and predicted results not mediocrity.The experiment results with 93.7% sparse degree show that the recommendation quality can be improved and that the best RMSE value,1.01,has been reached.

collaborative filtering;recommendation algorithm;sparsity;rating prediction;RMSE

2016-03-12

2016-06-22 网络出版时间：2017-03-13

国家级精品资源课程建设(007000523339)

蒋宗礼(1956-)，男，教授，CCF会员，研究方向为网络信息搜索与处理；王 威(1992-)，男，硕士研究生，研究方向为推荐算法。

http://kns.cnki.net/kcms/detail/61.1450.TP.20170313.1545.002.html

TP301.6

A

1673-629X(2017)05-0001-05

10.3969/j.issn.1673-629X.2017.05.001