基于DPSIR模型与集对分析法的三峡库区水生态安全评价

黄文琳+王鹏+杜温鑫+吴培森

[摘要]文章的目的是通过建立合理的模型来评价三峡库区的水生态安全状况，从而促进三峡库区更长久、稳定地发展。根据对三峡生态系统各项数据的研究，文章选取了其中具有代表性的指标，并建立了DPSIR模型，并对集对分析法的计算方法及指标进行了修正。最终通过计算联系度，得出不同年份的水生态安全等级。从过程中可以看出集对分析法的便捷性和可行性，从结果来看，随着人们环保意识的不断增强，虽然三峡库区水体灾害仍有发生，但是从模型所选取的指标角度上看，三峡库区的水生态安全状况却在逐渐恢复。

[关键词]水生态安全状况；DPSIR；集对分析法；模糊评价方法

[DOI]1013939/jcnkizgsc201714033

近年来，随着人们环保意识的不断加强，越来越多的人意识到水生态安全的重要性。随着三峡水电的落成，三峡库区长江段俨然由天然河道变成了目前世界上最大的人工湖泊。从2001年至今，库区蓄水越来越深，加上人们生产生活中的废水、船泊污水的排放等因素，三峡库区的生态环境态势严峻，支流等地发生水体水质灾害的频率也越来越高。为了对三峡库区的水生态安全现状有一个较好的掌握，并希望服务于三峡库区水资源、生态管理与保护，本文试图通过建立一种评价模型来衡量三峡库区的水生态安全状况。

1文献综述

关于湖泊、河流的评价体系已经由许多学者进行了相关的研究，并且提出了很多相关的评价模型。萧长来[1]采用均值化综合污染指数法对前郭灌法的水质进行了综合评价，获得了符合水质实际情况的结果，为治理污水提供了科学依据，具有一定的推广性。刘哲等[2]运用层次分析法对福州山仔水库生态环境进行了评价，确定出湖泊中污染因子的权重关系，获得了较为满意的结果，说明了层次分析法在定量计算污染指标的权重方面具有一定的适用性。沈迅伟等[3]采用传递包法进行模糊聚类分析并通过模糊聚类动态图对水域进行划分，再利用隶属函数对水质进行了模糊综合评判，为水污染环境评价提出了一套科学的评价方法。王李管等[4]建立了环境质量评价人工神经网络模型对大气质量和水质进行了评价，并将结果与模糊数学法及灰色聚类法所得结果进行了对比，验证了其模型的可靠性。谢先全等[5]采用灰色聚类和模糊聚类等方法对福建沿岸9个港湾的海水水质进行了定量分类评价，与1999年福建省海域环境的综合调查报告的评价结果相当吻合，为水质的污染治理以及水资源的开发利用提供了一定的科学依据。

综观水生态安全评价的相关文献，现有研究提出的评价模型大多是综合污染指数法、层次分析法、灰色聚类法等，这些方法各有其优点，但在评价的客观性和全面性方面还有待于进一步改进。由于水生态具有较为明显的模糊性，而模糊评价方法能有效地解决不确定因素对于结果的影响。有鉴于此，本文尝试对已有湖泊水生态评价模型的指标进行修正，并结合层次分析法和熵权法确定的综合权重，建立综合评判模型，进而实现对水环境的综合评价。以期达到预期目标的前提下对三峡库区水生态现状进行评价。

2基于DPSIR框架的水资源安全评价指标体系构建DPSIR框架是联合国（UN）在1993年为综合分析和描述环境问题以及其和社会发展的关系提出的。DPSIR框架包含了社会、经济、政治、环境等要素：一方面，它可以說明社会、经济发展对环境造成了哪些影响；另一方面，它也说明了人类行为及其最终导致的环境状态对社会的反馈。在参考相关生态安全评价指标体系及《全国水资源保护规划技术大纲（2012年）》的基础上，初步确立水资源安全评价指标体系如下。

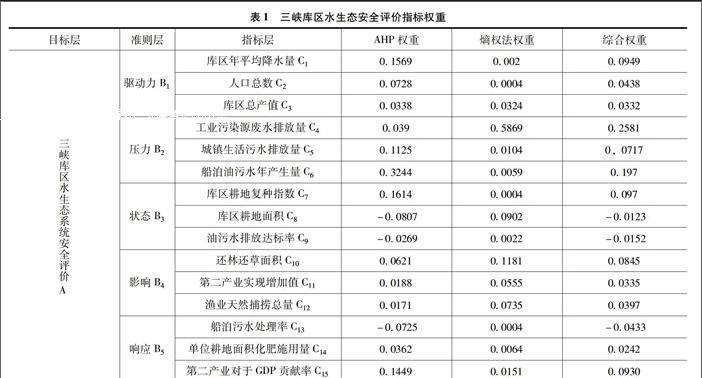
驱动力（B1）主要指人类社会经济活动，如人口增长、社会经济发展的需求、环境变化等。本文选取的指标有库区年平均降水量C1、人口总数C2、库区总产值C3。

压力（B2）主要反映水资源开发利用活动对生态环境造成的负荷，即自然条件和影响水资源安全的人类活动。本文选取的指标有工业污染源废水排放量C4、城镇生活污水排放量C5、船舶油污水年产生量C6。

状态（B3）主要指在上述压力下所处的状态，主要涉及水环境质量状况、生态系统所处状况等。本文选取的指标有库区耕地复种指数C7、库区耕地面积C8以及油污水排放达标率C9。

影响（B4）是指上述状态的改变对社会、经济、水生态系统环境产生的影响。本文选取的指标有还林还草面积C10、第二产业实现增加值C11、渔业天然捕捞总产量C12。

响应（B5）是指人类在经济社会活动中对水生态系统安全问题的能动反应，主要指采取维持水生态系统安全的响应措施。本文选取的指标有船舶油污水处理率C13、单位耕地面积化肥施用量C14、第二产业对GDP贡献率C15。

3基于综合权重的集对分析水生态安全评价模型

31集对分析法（SPA）

基于SPA的水生态安全评价的实质就是根据既定等级，依次计算测量值与不同等级的标准在指标所给的特性下的相似程度，如果两者相似则可归为一类，反之，则归为另一类。

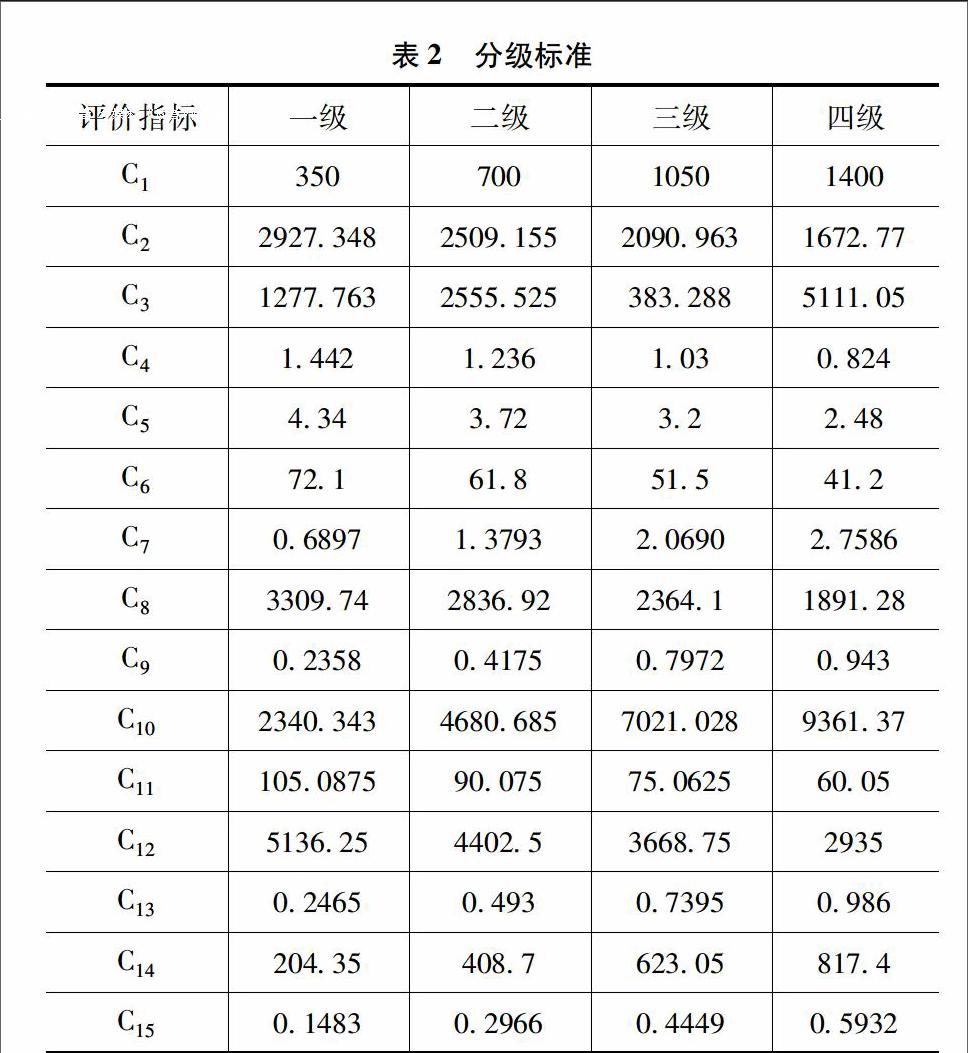
依据上文中的指标建立和指标等级的确立，将评价样本的某指标值，即测量值xl，m为指标集合总数，看成一个集合Xl（l=1，2，…，m），把相应指标的评价标准等级值看成另一个集合Yk（k=1，2，…，n），则Xl与Yk可构成一个集对（Xl，Yk）。一元联系度μl描述集对（Xl，Yk）的关系[6]

式（2）中ωl为第l指标的权重。在同一个评价系统中，有些指标的作用显著一些，有的作用则相对来说弱一些，因此各指标对μ的贡献度不同，可分别赋予不同的权重。在进行水资源系统评价时，关键在于确定上式中的μl。借助于模糊分析，给出联系度的具体计算公式：本文中取Ⅳ级为评价级别中的最高级指标。现在给出联系度的计算公式：其中，s1、s2、s3分别为Ⅰ级、Ⅱ级、Ⅲ级标准的上限值，超过s3即为Ⅳ级，s4为指标值在大于s3时所取得的最优值。在大多数情况下s4的值，依据实际情形而定。x为各指标的实际测量值。