大规模人群聚集活动网络关注的信息熵计算

陈玉萍

（安徽公安职业学院科信部，安徽合肥230031）

大规模人群聚集活动网络关注的信息熵计算

陈玉萍

（安徽公安职业学院科信部，安徽合肥230031）

随着社交网络的发展，人们在网络上对大规模人群聚集活动的关注也越来越深刻地影响着现实社会的活动.由于缺乏有效的技术手段，信息处理的效率受到了限制.提出了一种新的大规模人群聚集活动信息熵的计算方法，其基本思想是首先对大规模人群聚集活动信息内容进行建模，然后以香农信息论为理论基础，对大规模人群聚集活动的多维随机变量信息熵进行计算.该方法为大规模人群聚集活动的定量化分析提供了一个重要技术指标，为进一步的研究工作打下基础.

社会计算；大规模人群聚集活动；香农信息论；信息熵；最大熵理论

0 引言

信息技术的快速发展推动了生活、生产方式的巨大变革[1-3]，基于Web 2.0基础的信息技术更是引发了网络社交的繁荣发展[4-5]，通过这种方式，公众的信息意见能够快速、充分地利用网络社交平台得到反馈，对于社会的影响力也在不断增强[6-8].尤其是近两年，国内频繁发生大规模的群体聚集活动，这就要求政府应该加强对互联网信息平台的管理，能够及时关注网络上的舆论导向，并且要求能够从中快速对相关事件信息进行分析整理，这也是当前社交网络发展中所应当重点开发和研究的领域[9-12].

而对于群体性事件其影响程度以及重要程度的衡量，要求制定更加科学合理的方法，对于事件的衡量，如果仅仅通过网民反馈，得到的结果不仅不全面而且也是不够细致深入的.这种事件分析机制不仅不能够对于事件本质进行有效的分析，而且得到的结果也是存在着较大滞后性，甚至可能得到误导性的结果[13].同时，基于当前所形成的计算方法，主要用于交互关系计算、媒体挖掘等方面[14-15].关于公众意见分析的相关研究仍旧是相对滞后的，与之对应的理论体系尚未能够有效建立，特别是在量化分析指标上仍旧是相对缺失的，故此，需要通过社会计算方法实现对此问题的充分解决.

当前，大规模人群聚集活动的文本方式已经成为了实现信息传播的重要方式，通过对其中的信息量进行分析，能够对事件的影响力、舆论导向能力形成更加清楚、明确的量化分析指标.本研究中，提出了一种新的大规模人群聚集活动信息熵的计算方法，利用了最大熵等理论，对大规模人群聚集活动的多维随机变量信息熵进行计算.

1 大规模人群聚集活动数学模型

1.1 大规模人群聚集活动的分析模型

图1展示了网络文本事件的基本结构图.在计算信息量时，需要完成的基本工作就是对整个大规模人群聚集活动的基本构成进行分析.分析该结构图能够得出主体、地点、时间、数量、未抽取信息，构成了主要的信息内容.除了基于事件主体所具有的不同的属性特征，其他的影响因素还包括分析社会（自然）角色、社会（自然）关系、主体行为、所属机构体系等，而对于事件而言，具有的属性仅有一个：社会（自然）类别.

设事件信息为全集U，由n个子集U1，U1，…，Un构成，其中取10，U1表示事件主体集合，U2则代表了社会（自然）角色集合，U3代表社会（自然）关系，U4指的是所属机构或体系集合，U5为时间信息集合，U6为主体行为集合，U7为地点集合，U8为数量集合，U9为事件社会（自然）类别集合，U10指代了未抽取信息.依据定义能够得出满足U=U1∪U2∪…Un.

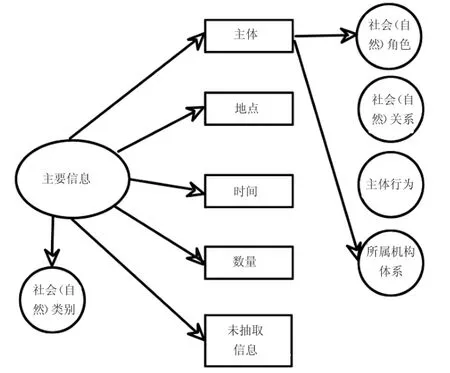
图1 大规模人群聚集活动结构

通过上述分析能够得出，其中包含的基本要素有5个，关联属性有5个，该结构方式对于大规模人群聚集活动的研究与分析是最为简单的，也是经过简化之后的方法.其中涵盖了几乎所有的大规模人群聚集活动文本信息.

研究发现，整个条件信息量会受到属性、要素之间彼此作用的影响，而发生变化.关于图1中的信息模块，其是基于文本信息抽取项的相关研究，其中涉及的研究对象有主体、时间、机构等.如果在一个大规模人群聚集活动中，包含的随机变量有n个，那么此时可以以X=（X1，X2，…，Xn）代表整个事件，故此时的事件组成为随机信息系统.

依据哲学相关理论，对于一个系统而言，其中的构成部分彼此之间是相互关联的.故此，尽管图1表现出的属性与要素数量都是相对较少的，但是彼此之间的关联性是十分复杂的，在图1中仅对其中简单的隶属关系展开论述.

1.2 基于多维随机变量构建大规模人群聚集活动分析模型

此时构成大规模人群聚集活动的随机变量数量共有n个，则此时可以通过（X1，X2，…，Xn）来代表整个随机事件，故此，随机事件本质上是一个随机信息系统，可以用X表示.

此时我们指定其中包含的随机变量数量为10，此时将活动的主体名称以X1代表，将其中的社会角色以X2代表，用X3以代表社会（自然）关系，则X4指的是主体所属机构、体系，X5指代了时间信息，X6则代表了主体行为，X7为地址信息，X8代表了数量信息，X9代表了舆情类别，X10指代未抽取信息.

2 计算大规模人群聚集活动熵

2.1 香农信息熵

人类针对信息的研究中，实现的重大突破就是实现了对信息的有效度量与计算，其中最具代表性的就是香农理论，下面对其进行简单阐述：

熵（entropy）这一概念是该理论最具代表性的特征体现，该理论论证了信息的不确定性与其熵之间是存在着一定的对应关系.

定义：对于一个随机变量而言，其熵H（X）可界定为：

由式（1）能够得出，此时熵H（X）为服从于p（x）的概率分布函数，X中具有的平均信息都能够通过该熵得以分析.将通过该公式对于大规模人群聚集活动信息熵展开论述分析.

2.2 最大熵理论的计算方法

2.2.1 最大熵的数学表示

1）如果此时的约束条件是给定的，那么依据最大熵原理可以得到最佳的概率分布，此时的问题就转换成为了拉格朗日方法求极值的问题.

2）计算过程

求n元函数的f（x1，x2，…，xn）在m（m＜n）个约束条件下的条件极值，常数1，λ1，λ2，…，λm依此乘f，φ1，φ2，…，φm然后累加起来得到函数F（x1，x2，…xn）.

F（x1，x2，…，xn）=f+λ1φ1+λ2φ2+…+λmφm.（3）然后列出F（x1，x2，…，xn）无约束条件时具有极值的必要条件，

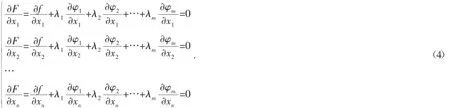
把这n个方程和m个约束条件方程进行联立，即可求出（n+m）个（x1，x2，…，xn），（λ1，λ2，…，λn）的值，由公式（4）可知，函数的一阶导数为零，则x1，x2，…，xn即为得到的极值点，也可将其称之为驻点.

基于熵F（x）函数为f（x）的泛函，此时通过拉格朗日方法得出的解值为而非.

2.2.2 离散型随机变量的最大熵分布形式

假设此时X为离散型随机变量，而且其可取值x1，x2，…，xn，相应的概率记为p1，p2，…，pn，则H（x）最大的充要条件

对pi求偏导数，根据求取最值的必要条件，得到方程组：

求解：pi=exp（λ-1），为常数.

如果离散随机变量可取值的个数是有限的，那么此时如果其对于每一个取值都具有相同的概率，那么此时得到的信息熵是最大的，此时得到的即为最大熵分布.

由此能够得出结论，从中得到函数，该函数是严格单调函数，这是本研究中得出的重要结论，依据该结论能够实现对大规模人群聚集活动的有效计算，而且能够保证结果是严格单调的，见图2.

图2 熵H（x）函数的单调性

3 基于最大熵理论对大规模人群聚集活动信息熵进行计算

3.1 构建分析模型

此时可以X=（X1，X2，…，X10）代表大规模人群聚集活动，其中X1：主体，X2：角色，X3：关系，X4：所属机构、体系，X5：时间，X6：行为，X7：地点，X8：数量，X9：类别，X10：未抽取信息.

3.2.构建知识库

设Xn为大规模人群聚集活动中的某个分变量，此时如果以M代表其取值结合，满足M1，M2，M3，…，Mn⊂M，同时满足M1∪M2∪M3∪…∪Mn⊂M.

下面以大规模人群聚集活动的计算为例，对9个随机变量的取值集合问题展开论述分析，提出本研究的信息熵计算方法，其中选择的关键词都是富有代表性的，并且利用这些关键词集合得到了知识库，利用该知识库能够对这9个变量的取值集合进行充分的考察，对此进行简单描述.

3.2.1 变量X1（事件主体名）取值范围

主体名称可以是地点名称、机构或人物名称等，此时将其依据子集进行分类，当有一次关键词匹配的时候，q1=1，若无则取q1=0.

通过上述分析能够得出，X1代表了事件主体名称，为离散随机的，以M代表其取值的集合，其中满足M1，M2，M3，M4■M，并且M1∪M2∪M3∪M4⊂M.

基于公众对于一般信息的敏感情况，可以将知名度进行类别划分，并将其与主体取值的子集一一对应，此时M4代表了取值的基本集合.

依据公众信息敏感度可做如下划分：

M1信息敏感度度第一等级，此时可继续进行分子集的划分L1，L2，…；L1运动名人；

…

M4第四等级，同样继续划分子集L1，L2，….

本研究中，对于等级的划分主要目标是为了简化问题，以实现对此类问题的更好说明，而且如果此时存在与取值相匹配的值，则此时取值为1.关于加权值的计算方法将在后续研究中不断完善.

即当X1=x1，若x1∈M1-M4，此时得到q1=1，否则q1=0，其他情况与之类似.

可将形式化命题逻辑判断作出如下说明：

通过上述分析能够得出，匹配计算即为对一阶谓词进行逻辑判断.

命题A：X1存在一个取值，即当X1=x1，逻辑为真.

命题B：当x1∈M1或x1∈M2或…或x1∈M4，只要其中有一个是成立的，那么此时证明逻辑为真.

如果A∧B合取式为真，则此时说明q1存在一次取值1.

反之，如果A∧B为假，则此时q1有取值0.此时未对计算作出贡献.

3.2.2 X5变量（时间信息）的取值范围

X5代表了事件时间信息，整个取值集合为M，其中包含的元素是各个时段，M1，M2，M3，…，M6∪M为其中的子集，满足M1∪M2∪M3∪…∪M6∪M.

进行一阶谓词逻辑判断：

命题I：X5有一个取值，即当X5=x5，逻辑为真.

命题J：当x5∈M1或x5∈M2或…或x5∈M6，或中一个成立时，逻辑为真.

如果I∧J的合取式是真的，那么此时q5取值1.

反之，如果I∧J合取式为假，此时q5取值0.此时并且对计算值产生影响.

3.2.3 X7变量（地址信息）的取值范围

此时X7代表着事件的地址信息，属于离散型的随机变量，此时以M代表其取值范围其中涵盖了若干子集M1，M2，M3，…，M14∪M，满足M1∪M2∪M3∪…∪M14∪M.

进行一阶谓词逻辑判断：

命题N：X7有一个取值，即当X7=x7，逻辑为真.

命题O：当x7∈M1或x7∈M2或…或x7∈M14，或当其中有一个是成立的，那么此时判断逻辑为真.

则当N∧O的合取式为真时，表示q7有一次取值，为1.

当N∧O的合取式为假时，表示q7有一次取值，为0.这种情况下，对计算值无贡献.

3.3 大规模人群聚集活动信息熵的计算公式

该问题的计算本质上是在一定的条件限制下，求解最大熵的问题，此时的熵函数在形式上与一维随机变量是类似的，而且此时熵值可为任意正数.

当取得最大熵值时，此时得到的联合分布将会呈现出均匀分布的特征，分变量的取值见表1，具体计算公式如下：

用qi表示随机变量Xi的取值次数总数，当有一次基本集合的取值时，q1=1.

由约束条件可知：p（x1，x2，…，x，则熵函数表示为：

表1 分变量的取值

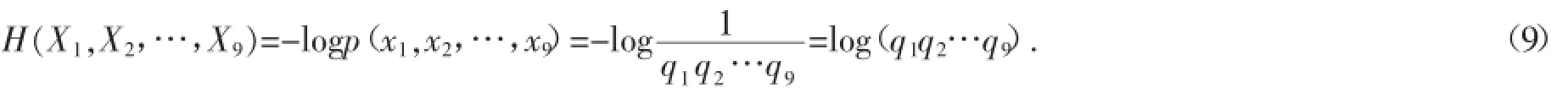
利用该公式能够实现大规模人群聚集活动的信息熵计算，而且能够得出公式是严格单调的.

4 实验

4.1 计算信息熵

计算信息抽取形式的“WTA本周看点：科贝尔争卫冕大威盼摆脱一怪圈”的信息熵值，对于qi值采取逐项计算匹配的方式，见表2.

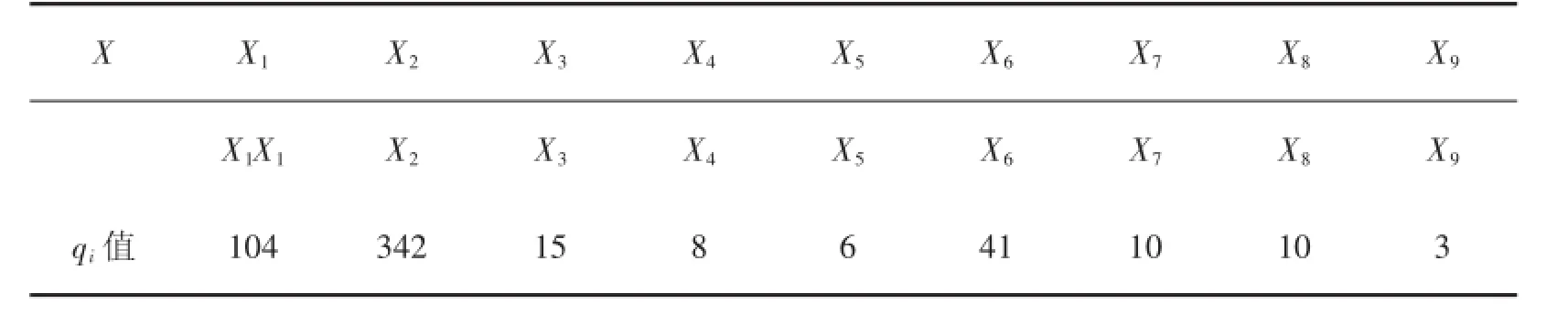
表2 X的加权值

此处采取的是自然对数的计算方法：H=ln（104×342×15×8×6×41×10×10×3），保留到小数点后两位.

4.2 对比分析同类事件的熵值大小

本研究基于2016年发生的大规模人群聚集活动，展开了案例分析.从中进行了信息提取与筛选，而且经过了十分复杂的计算，得到了最终的计算结果如下表3所示，此时熵值1代表的是抽取信息之后得到的计算结果，通过本实验能够对算法单调性进行论证，并且对比分析不同事件中涵盖的信息量大小.

综合表3数据结果，能够得出趋势图，见图3，对此进行分析能够得出，此时呈现出一种单调变化的趋势关系.而且通过该趋势图也能够论证本研究方法是正确、合理的.

由此能够得出，最小熵值事件为“吉奥尔吉拒参加联杯因不满意大利网协强硬态度”，值为20.14，分析其原因，由于该事件的文本信息十分短，整个事件尚处于爆发的初期阶段，此时内容里面涵盖的信息量也是比较匮乏的.具有最大熵值的为“休斯顿赛2号种子吞完败出局郑泫逆转本土选手”，因为种子选手完败，整个文本内容包含了极为丰富的信息，此时得到的信息量更加接近于直觉感官.

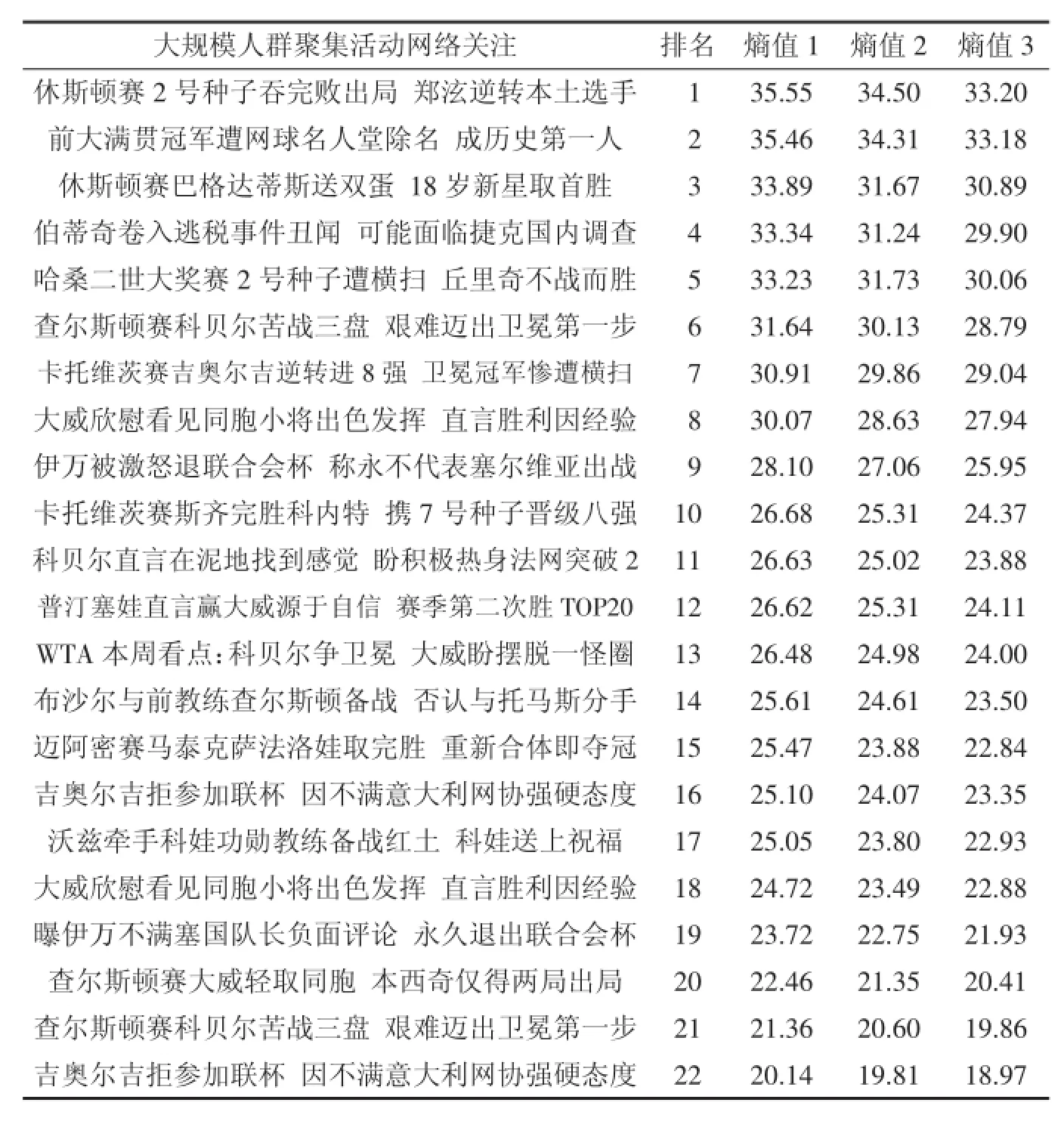
表3 计算结果排序

图3 计算方法的合理性验证

4.3 信息抽取方法对整个结果的影响

信息抽取方法必定会对整个的熵值计算产生影响，故此，想要获得更加合理的计算值，要求进行如下两步操作：

1）过滤重复项：指的是对于期间重复出现的内容进行有效的过滤，得到结果如表3第2列.

2）共指消解：在完成过滤之后，需要进一步实施共指消解处理，对于其中的冗余信息进行消除，得到结果表3第3列项所示.

图3展示的为进行了信息抽取之后的结果，此时将其与图4即同时进行了过滤与消解两个步骤的结果进行对比，此时得到的熵值差距不大的事件在排序上是存在差异的，但是结果的单调特征并未受到影响.

图4 对比试验

经过上述实验能够得出，对于类型不同的事件，当进行了过滤、共指消解操作后，产生的影响效果是一致的，都会使得熵值有所降低.

5 结束语

结合最大熵与香农理论，针对大规模人群聚集活动如何实现对其信息熵的有效计算提出了可行性算法，实现对该事件的定量性分析.所使用的方法是对于最大熵理论的有效运用，而且对于解决社会中的其他定量分析问题也是具有重要的借鉴作用的.本研究算法的设计依旧是以当前的社会计算理论为依据的，因此仍需要在后续的研究实践中不但加强对此类方法的研究与分析.

参考文献：

[1]SPARAVIGNA A C.Mutual Information and Nonadditive Entropies：A Method for Kaniadakis Entropy[J].International Journal of Sciences，2015，4（10）：5-8.

[2]HOIL，SHIHSC，TSAICP，etal.CombiningGreyRelationalAnalysisandInformationEntropyforGovernmentDecisionMaking[J].InternationalJournalofKanseiInformation，2015，6（3）：53-62.

[3]TSERKISST，MOUSTAKIDISCC，MASSENSE，etal.QuantumTunnelingandInformationEntropyinaDoubleSquareWellPotential：TheAmmoniaMolecule[J].PhysicsLettersA，2014，378（5）：497-504.

[4]VladimirHnizdo，JunTan，BenjaminJ.Killian，etal.EfficientCalculationofConfigurationalEntropyfromMolecularSimulationsbyCombiningtheMutualinformationExpansionandNearestNeighborMethods[J].JournalofComputationalChemistry，2008，29（10）：1605-1604.

[5]HESSLINGJP.SubjectivityinApplicationofthePrincipleofMaximumEntropy[J].OpenJournalofStatistics，2013，3（6）：1-8.

[6]SZEGA M.Application of the Entropy Information for the Optimization of an Additional Measurements Location in Thermal Systems[J]. ArchivesofThermodynamics，2011，32（3）：215-229.

[7]SABIROVDS，OSAWAE.InformationEntropyofFullerenes[J].JournalofChemicalInformationandModeling，2015，55（8）：1576-1584.

[8]SHIL，LUOF.ResearchonRiskEarly-WarningModelinAirportFlightAreaBasedonInformationEntropyAttribute Reduction and BP NeuralNetwork[J].InternationalJournalofSecurityandItsApplications，2015，9（10）：313-322.

[9]MoritaM.Measuringcosmicinhomogeneitieswithinformationentropy[C]//AmericanInstituteofPhysics，2013：97-100.

[10]MRAZOVACB，BJELICAMZ，KUKOLJD.Device-freeIndoorHumanPresenceDetectionMethodBasedontheInformationEntropyof RSSIVariations[J].ElectronicsLetters，2013，49（22）：1386-1388.

[11]FERREIRARC，BRIONESMRS.PhylogeneticEvidenceBasedonTrypanosomaCruziNuclearGeneSequencesandInformation EntropySuggestthatInter-strainIntragenicRecombinationisaBasicMechanismUnderlyingtheAlleleDiversityofHybridStrains[J].Infection，GeneticsandEvolution，2012，12（5）：1064-1071.

[12]SABIROV D S，SHEPELEVICH I S.Information Entropy of Oxygen Allotropes.A still open Discussion about the Closed Form of Ozone [J].ComputationalandTheoreticalChemistry，2015，1073：61-66.

[13]WELTMANJK.MappingZaireEbola Virus Glycoprotein Organization onto Information Entropy[J].Chinese Optics Letters，2015，10（9）：090501.

[14]SANDSD，DUNNING-DAVIESJ.Information，Entropy，andtheClassicalIdealGas[C]//ThePhysicsofReality：Space，Time，Matter，Cosmos.WorldScientific，2013，1：196-206.

[15]VIEIRATM，VISWANATHANGM，DASILVALR.InformationEntropyofClassicalVersusExplosivePercolation[J].TheEuropean PhysicalJournalB，2015，88（9）：213.

（责任编辑王颖莉）

Information Entropy Calculation of Network Attention in Large-scale Population Gathering Activities

CHEN Yu-ping
(Department of Science&Technology Information,Anhui Vocational College of Public Security,Hefei,Anhui 230031,China)

Along with the development of the social network,people’s attention to large scale population gathering activities in the network has become more and more profoundly influential to the activities in the real society. Due to the lack of the effective technical means,the efficiency of information processing has been limited.This paper puts forward a new computation method for large scale population gathering activities information entropy,the basic idea of which is to first carry out modeling on large scale population gathering activities information content.And then,based on the theory of Shannon information theory,it performs computation on the multidimensional random variables information entropy of large scale population gathering activities.

social computing;large-scale population gatheringactivities;Shannon information theory;information entropy

TP393

A

1673-1972（2017）03-0065-08

2017-03-11

安徽省教育厅自然科学研究项目（KJ2017A865）

陈玉萍（1978-），女，安徽霍邱人，讲师，主要从事计算机应用研究.