空心激光辐照薄膜产生温度场与应力场的数值模拟与分析

田东飞，毕娟，陈桂波，张烨，张佳佳

（长春理工大学 理学院，长春 130022）

空心激光辐照薄膜产生温度场与应力场的数值模拟与分析

田东飞，毕娟，陈桂波，张烨，张佳佳

（长春理工大学 理学院，长春 130022）

为了考察空心激光辐照下膜层的温度场及应力场的分布特征，基于传热学及弹性力学理论，建立空心激光与膜层相互作用的热应力模型。利用有限元数值分析方法求解物理模型，通过对数值结果的分析，可以得出随着激光能量的增强，温升增大，其应力也随之变大的特征及变化规律。其结果可为激光与光学薄膜相互作用提供一定的理论依据。

空心激光；温度场；应力场

空心激光束（Hollow Laser Beam，HLB）是通过激光整形技术获得的一种在传播方向上中心光强为零的环状光束。1971年，Ashkin A等人用光学镊子囚禁微米粒子，利用强聚焦的高斯激光束在焦点附近产生较大的电场梯度，对激光束中介质粒子施加一个指向焦点的作用力，使得介质粒子被三维囚禁在高斯光束的焦点附近［1］。1995年H.He通过将一束线偏振He-Ne高斯激光束照射到衍射效率为30%的计算全息光栅得到空心高斯光束［2］。2010年，Zhang Y等人通过腔内变换建立了空心高斯光束模型，发现空心高斯光束具有独特的传输特性，在近场有很好的传输稳定性，而在远场时轴上的光强为最大［3］。

光学薄膜在光学遥感器、通讯技术、光学窗口等领域有广泛的应用。当激光与薄膜相互作用时，薄膜材料对激光的本征吸收、杂质吸收以及制备过程中引入的附加吸收，导致了激光能量在薄膜内沉积转化为热能，形成温度场分布。温度升高到一定程度，薄膜会发生熔融或热应力破坏。研究人员将光学薄膜元件抗损伤能力不断提高，开发新型的抗激光损伤的光学薄膜。2007年，Gallais L研究了波长为1064nm的激光脉冲对硅薄膜的破环机制，通过光学显微镜对其进行分析，此次实验基于对材料达到激光损伤阈值的观测，从而对增强光学薄膜抗损伤特性进行分析［4］。2013年武汉理工大学程芸等人对氮化硅透明光学薄膜的制备与分析进行了研究［5］。

随着激光技术向着高功率高能量方向发展，目前激光与光学薄膜器件的相互作用成为研究热点。在2012年南京理工大学的王斌对比研究了长脉冲激光和短脉冲激光与光学薄膜作用所导致的损伤，分析改进长脉冲激光与增反膜和高透膜作用的模型，然后根据数值模拟探讨出在光学薄膜的损伤主要是由材料的表面缺陷和内部缺陷所导致的。同时研究了电化学损伤对光学薄膜的影响。对比分析了长脉冲激光与短脉冲激光对光学薄膜作用的机理，通过形貌损伤对长脉冲激光和短脉冲激光对光学薄膜作用的不同机理进行研究［6］。然而关于空心激光辐照薄膜材料热力效应的研究仍然较少，随着空心激光的广泛应用，在工作生产中常会出现薄膜损伤问题，因此研究多膜层结构的空心激光激光损伤特性对其在科研及生产中的应用具有重要的实际价值。

本文根据传热学理论，基于有限元方法，建立双层膜层结构模型，对空心激光辐照光学薄膜产生温度场和应力场进行数值模拟与分析，得到温度场与应力场的分布特征及变化规律。

1 物理模型

空心激光辐照光学增透膜，空心激光作用在膜层材料上的横截面以及强度分布如图1所示，其中ω为空心激光半径，ω0是暗斑的半径，r0定义为最大径向强度位置和光束中心之间的距离，即光束半径。

图1 空心激光的横截面以及强度分布

考察的光学增透膜由SiO2、Al2O3和Ge基底组成，增透膜层的厚度分别为H1=77.7nm，H2= 95.5nm。

图2 增透膜的模型示意图

图2为增透膜的模型示意图。使用波长为1064nm的激光辐照增透膜，其光强可以表示为：

其中，e是自然数，I(r)是激光强度，r是空心激光的径向坐标，P为空心激光峰值功率。

1.1 热传导方程

本文研究的薄膜材料在几何形状为圆形的Ge镜上，为了减少模拟计算量，将三维模型简化为二维轴对称模型。

二维轴对称模型下的热传导方程：

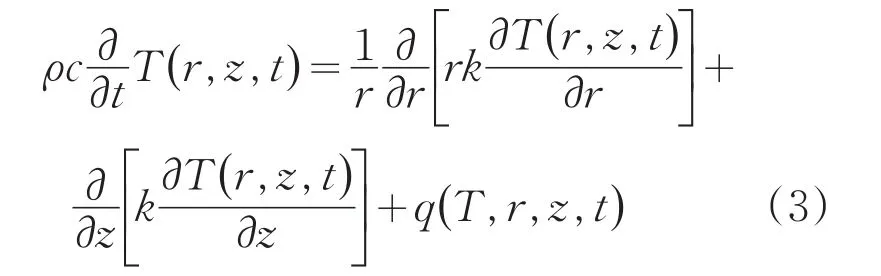
空心激光的暗斑半径公式是［7］：

其中，T(r,z,t)代表t时刻的温度分布，ρ、c、k分别是密度、比热容和导热系数；热源项表示为：

其中，R(T)是材料的反射率，α(T)是材料的热吸收系数，激光脉冲的时间分布函数g(t)可以表示为：

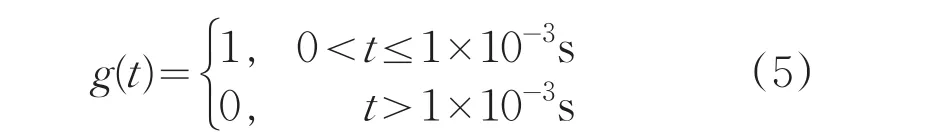
通过最终的求解可得到材料内部的温度场分布。

1.2 热弹性方程

空心激光与材料相互作用时，材料内部的瞬态温度场分布会使得材料产生不均匀膨胀，其原因是材料一般都具有热胀冷缩特性。由于材料受到约束作用使物体产生热应力［8，9］。

利用弹性力学中的几何方程、物理方程和平衡方程可以得到与热传导方程相耦合的平衡微分方程，可表示为：

r方向：

其中，ur为r方向上的位移分量，μ为泊松比，ε是体应变量，uz为z方向上的位移分量，β是热应力系数。

开始没有发生位移处于静止状态，初始条件为：

假设处于真空中，外界对材料无任何作用。根据几何方程可以得到应变向量：

εr为径向体应变量，εθ为环向体应变量，εz为轴向体应变量，εrz为切面体应变量。

根据胡克定律便可得到应力向量：

其中，σr表示径向应力，σz表示轴向应力，σθ表示环向应力，τrz表示切面应力，E表示弹性模量，C表示刚度矩阵，ε0则表示由热膨胀产生的初始应变向量，a0表示热膨胀系数。

1.3 网格的剖分方法

薄膜在激光作用下会出现破环累积，当膜层材料不同、膜层数不同以及膜层厚度不同时，薄膜破坏所产生的应力也不尽相同［10］。本文利用有限元数值分析方法求解物理模型，建立了双层增透膜的模型，在单元内设置位移坐标的分量。因为是线性插值函数，将函数定义在每个单元格中，当单元格足够小时，就可以近似假设所求得的值为接近于真实的值［11，12］。

图3 有限元网格剖分示意图

2 模拟分析

空心激光辐照由SiO2、Al2O3和Ge基底组成光学增透膜，材料参数如表1所示。首先模拟空心激光不同半径下的温度随时间的变化。

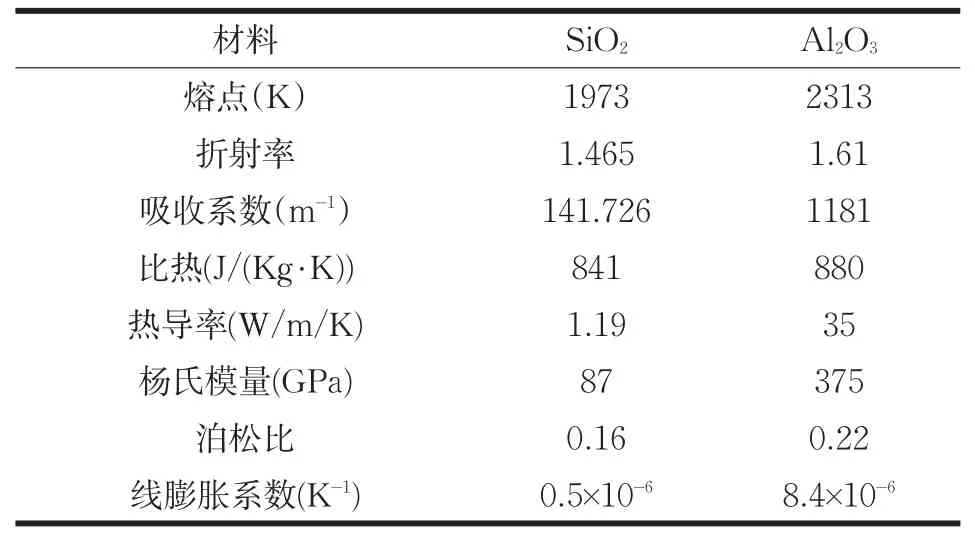
表1 材料的物理参数

图4（a）可以看出，温度随着径向距离的增大而逐渐升高，但当达到径向距离的边缘处时温度逐渐下降且接近平缓。图4（b）可以看出在1ms时刻，表面的中心点温度最高。本文激光光源采用的是空心激光，虽然激光能量密度在目标表面中心点为0，但由于温度的传导作用使得温度在1ms时刻，表面的中心点温度最高。由于空心光源是中心光能量密度为0，中心处的温度由于热传导的作用导致激光能量中心点产生了会聚。导致表面中心点温度在1ms后继续升高。光斑能量最强点温度随时间的变化曲线如图4（c），可以看出空心激光半径越小温度越高。产生这种现象的原因是由于目标吸收率随着温度的升高而快速增大导致温度随时间的变化不是直线上升，对于激光能量增强温升速度增快，而当光斑半径为2mm时，吸收率较低所以温升不明显。

图4 空心激光作用在增透膜上不同空心激光半径下的温度随时间的变化曲线图

从图5（a）中可以看出目标中心点温度随着能量增大而升高。这是由于能量密度变大而激光半径不发生改变，从而导致能量密度越高，则温度上升越明显。从图5（b）可以看出在表面能量最强点的数值结果与中心的数值结果点的相近，只是温度变化相对较高，在激光辐照时间内温度随时间变化呈上升趋势，当辐照时间结束时，温度逐渐下降，随着时间的变化，曲线略有平缓。

图5 不同激光能量条件下目标中心点温度及能量最强点温度随时间的变化

膜层结构的熔点为1943K，Ge基底熔点为1210K。与模拟数据进行比对，可以看出薄膜层和基底层都没有受到热损伤。

图6 不同能量条件下目标表面径向应力和轴向应力随径向坐标的变化

图6（a）中可以看出，随着激光能量的增强，目标表面的温度明显越高，应力也随之增强。径向应力随着径向距离的增加逐渐有减缓的趋势，当到达最大压应力的时候，压应力逐渐减缓，直至压应力为零，再随着径向距离的增大，径向应力表现为拉应力，拉应力随径向距离的增大而略有上升，当到达一定距离时，拉应力略有下降。

图6（b）表示激光能量分别为：60J、80J、100J时目标表面轴向应力随径向坐标的变化曲线图，从图中对比可以看出：随着能量密度的逐渐增大，其载荷越强，对应的应力越强。轴向应力的变化幅度随着径向距离的变化不大，可以看出能量越大其温升变化越大，温升变化进而产生热应力，热应力变化越大，在图中产生热应力的变化位置在径向距离为距离光斑不远处（5mm）。

增透膜的抗拉强度为0.1035×108Pa，抗压强度为8.5×108Pa。对比图中应力变化可以看出拉应力与压应力都没有对膜层结构造成损伤。

3 结论

本文研究了空心激光作用在增透膜时膜层结构的损伤情况。通过对数值结果的分析可以得到如下结论：

首先激光功率密度是决定目标表面温度峰值的关键物理量之一，在给定激光脉宽的情况下，温度峰值随能量的增强而升高。在给定激光能量密度的情况下，温度峰值随着脉宽的增加而减小。与实心激光不同，空心激光导致目标表面不同位置点温度达到峰值时刻不同。在空心激光内部，温度达到峰值存在一定“延时”。温度梯度为热应力的载荷，增加激光能量，减少脉冲宽度均可使目标表面产生温度积累效应，因此应力的各分量均增强。

［1]Ashkin A，Dziedzic J M.Optical levitation by radiation pressure［J］.Applied Physics Letters，1971，19（8）：283-285.

［2]He H，Heckenberg N R，RubinszteinDunlop H.Optical particle trapping with higher-order doughnut beams pro⁃duced using high efficiency computer generated holo⁃grams［J］.Journal of Modern Optics，2007，42（1）：217-223.

［3]Zhang Y.Generation of three-dimensional dark spots with a perfect light shell with a radially polarized Laguerre–Gaussian beam［J］.Applied optics，2010，49（32）：6217-6223.

［4]Gallais L，Capoulade J，Wagner F，et al.Analysis of ma⁃terial modifications induced during laser damage in SiO2 thin films［J］.Optics Communications，2007，272（1）：221-226.

［5]程芸.氮化硅透明光学薄膜的制备与特性分析［D］.武汉理工大学，2012.

［6]Wang B，Qin Y，Ni X W.Effect of defects on longpulse laser-induced damage of two kinds of optical thin films［J］.Applied Optics，2012，49（29）：5537-5544.

［7]沈军，王珊，吴广明，等.多层高反膜的理论设计与光学特性分析［J］.同济大学学报：自然科学版，2005，33（5）：659-663.

［8]Li Z W，Wang X，Shen Z H，et al.Numerical simulation of millisecond laser-induced damage in silicon-based positive-intrinsic-negative photodiode［J］.Applied Op⁃tics，2012，51（14）：2759-2766.

［9]王茜.脉冲激光对半导体材料热力效应及在CIGS-、TFSC划线中应用［D］.南京：南京理工大学，2014.

［10]孙承纬，陆启生，范正修.激光辐照效应［M］.北京：国防工业出版祉，2002.

［11]毕娟，金光勇，倪晓武.532nm长脉冲激光致GaAs热分解损伤的半解析法分析［J］.物理学报，2012，61（24）：244209-244216.

［12]Ma J H，Wu G M，Cheng Y B，et al.Preparation of hy⁃drophobic optical silica thin film with sol-gel method［J］.Acta Physico-chimica Sinica，2001，17（12）：1112-1116.

Numerical Simulations of Temperature Field and
Stress Field Generated by Hollow Laser Irradiating Films

TIAN Dongfei，BI Juan，CHEN Guibo，ZHANG Ye，ZHANG Jiajia
（School of Science，Changchun University of Science and Technology，Changchun 130022）

In order to investigate the distribution characteristics of temperature field and stress field of the film irradiated by laser，the thermal stress model of the interaction between the laser and the film system is established based on the theory of heat transfer and elastic mechanics.The finite element method is used to solve the physical model.By analyzing the numerical results，the fol⁃lowing law is obtained.With the increase of laser energy，the temperature rise increases，and the stress of the laser becomes larg⁃er.The results can provide some theoretical basis for laser induced damage of optical thin films.

hollow laser beam；temperature fields；stress fields

O437

A

1672-9870（2017）02-0001-05

2016-12-14

田东飞（1989-），女，硕士研究生，E-mail：gannannu@163.com

陈桂波（1979-），男，副教授，E-mail：guibochen@126.com