精心设计问题串，提高课堂教学效益

江苏高邮市南海中学 管明贵

精心设计问题串，提高课堂教学效益

江苏高邮市南海中学 管明贵

质疑是数学的灵魂，数学的真正组成部分是问题和解疑。在数学课堂中，数学概念无不是从质疑、解疑、再质疑、再解释的过程中形成与认知的，新知识的巩固与拓展，学生思维方法的培养与提升，实际应用能力和创新能力的形成，这些过程都是从“问题”开始的。初中生的质疑能力还很稚嫩，尤其是数学课堂中问题的发现能力仍旧处于一个低层面，因此在教学中，需要根据具体的教学内容和学生的学情，设计并合理运用问题串来创设一个学生产生问题和解决问题的过程，将学生的思维由识记、理解、应用等较低层面推向分析、综合、评价等较高层面。如何才能精心设计问题串，提高课堂教学效益呢？本文就此谈谈自己在课堂教学中的一点实践，以期与同仁切磋和探讨。

问题串；质疑；解疑；课堂教学

在数学课堂中采用问题串，可以在学习某一主题内容时围绕一定目标展开，精心设计一串问题就需要按照一定逻辑结构“串”下去。构建适当的问题串是高效课堂的基本主线，课堂上的质疑、解疑，问题探究是教与学的一条不可缺少的途径。

一、将数学概念的学习采取问题串化，让学生在认知过程中理解概念的内涵与外延

教学实践表明，数学知识有许多难点比较抽象，学生初次接触不可能直接进行知识迁移，缺乏对数学概念的感性认识，尽管很多教师讲得口干舌燥，但学生仍云天雾地投入不到学习活动中去，与教学的预期效果有天壤之别。倘若在课堂上给出概念相应的问题情境，创设与之相应的问题串，将知识难点细化为一个个小问题，让学生在情境中质疑、解疑，循序渐进，课堂就会出现欣欣向荣的景象。

案例1：平行线的判定定理中提到的“同位角”的教学。

问题1：把两根小木条分别用四根小木条钉在一起，可以形成8个角，这8个角的大小是否可以改变？通过制作你想到了什么？

问题2：火车道、梯子、停车场画出的停车位等实际问题中（通过媒体展示图片），你认识了什么几何形状？试在纸上画出它的图形。

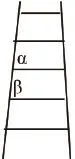
问题3：如果将梯子用图形简单地画成右图形式，那么∠α与∠β的位置有什么关系？二者一定相等吗？请你说明缘由。

问题4：看看身边是否有同位角的例子，能否找出相应的平行线。

本案例中的问题1是从学生的生活实际出发的数学实验，动态几何模型可以有效地帮助学生初步认识同位角的概念，从而让学生亲历知识的发生过程，给学生一个随手可及的实践与想象的空间。问题2在问题1的基础上让学生对几何形状有一个深入发展的展望，从而打破了直接给出“两条平行线被第三条直线所截”来认识同位角概念的单一教学模式，促使学生探究式的自主学习。问题3为学生学习平行线判定定理提供了探究“同位角相等，两条直线平行”这一性质的现实模型，让学生的数学思维潜移默化。问题4让学生再次回到生活，用概念去寻找生活中同位角的例子，体验到数学在生活中的应用价值。因此，对数学概念的问题串可以预设大量的生活背景的问题，让学生通过“做”数学开拓自己的思维空间，提升自己的自主探究能力。

二、将数学质疑或规律的学习采取问题串化，让学生在探究过程中由表及里、由浅入深

在课堂上对数学规律或质疑运用问题串进行处理，有效地引导了学生在质疑的环境中投入自主的探究过程，对数学规律就会有由表及里、由浅入深地构建的过程。所以，在设计问题串时需要把握问题的衔接与梯度，在集体备课时做到精细化，从而让学生在质疑的环境中主动追求知识，得出由未知向已知的发展。

案例2：“曲线与几何图形的面积”的总结性教学。

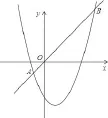
已知：如图，曲线 y=x2-2x-4 与直线y=x交于 A、B 两点，M 点在曲线上，且在直线AB的下方，连接 OM。

问 题1： 当M 为 曲 线 的 最 低 点 时，△OMB的面积是多少？

问题2：若△ OMB的面积为8 时，则M点的坐标是多少？

问题 3：当点 M 在曲线对称轴的右侧时，△ OMB 的面积最大时，M点的坐标是多少？

问题 4：若 OM 与直线 AB 垂直时，则点 M 的坐标是多少？

本案例是一道基础整合题。其中问题1是常规问题，用三角形的三个顶点坐标求面积较为简单，是为后面问题的探究埋下伏笔。问题2则是在问题1的基础上反向思考，学生假设M点的坐标即可找到。问题3的思考方向有类似于问题2的过程，只不过是利用了三角形面积的最大值，这就有效地发展了学生的智能。问题4仅仅是问题2的知识迁移，只不过是呈现问题的方式变了，更加重视问题本质的训练，能够快速提升学生对问题处理的能力。这四个问题渗透性极强，但又层面不同、角度不同，让学生在“圈套”中探究，在思考中前行，让不同层面的学生都能从中亲历到成功的愉悦。因此，在设计问题串时，必须考虑到从特殊到一般，由静入动，在知识的迁移中创设具有新颖性的问题。

总之，正确运用问题串有利于发展数学课堂教学的过程，也就是说，挖掘有价值的问题串是课堂的“精髓”，内涵深奥的问题串的设计和运用启迪着学生的创新思维，直接影响着学生在课堂探究中学科素养的提升。因此，唯有精心研究以问题串为载体的教学脉络，才能有效地拓展教师和学生的发展空间，才能让课堂和谐精准、朝气蓬勃。

[1]李 键 ．精 心 设 计 问 题 串， 提 高 课 堂 教 学 效 益 [J]．中 学 数 学，2011（6）：7-9．

[2]黄智谨 ．精心设置“问题串”提升数学课堂教学效益 [J]．中学数学研究：华南师范大学版，2014（9）：30-32．

[3] 郑长权 ．精心设计问题串 提高生物教学有效性 [J]．中学课程辅导：教师通讯，2012（1）：76-77．